字符串的排列
题目
给定两个字符串 s1 和 s2,写一个函数来判断 s2 是否包含 s1 的排列。
换句话说,第一个字符串的排列之一是第二个字符串的子串。
示例1:
输入: s1 = "ab" s2 = "eidbaooo"
输出: True
解释: s2 包含 s1 的排列之一 ("ba").
示例2:
输入: s1= "ab" s2 = "eidboaoo"
输出: False
注意:
1.输入的字符串只包含小写字母
2.两个字符串的长度都在 [1, 10,000] 之间
枚举法
首先,罗列第一条字符串中字符的所有排列,再逐一检测是否被第二条字符串包含。
罗列所有排列可以递归的形式描述为:
- 从有序序列中取出一个元素,再求由剩余元素组成的所有排列
- 将第一个元素分别拼接剩余元素的所有排列
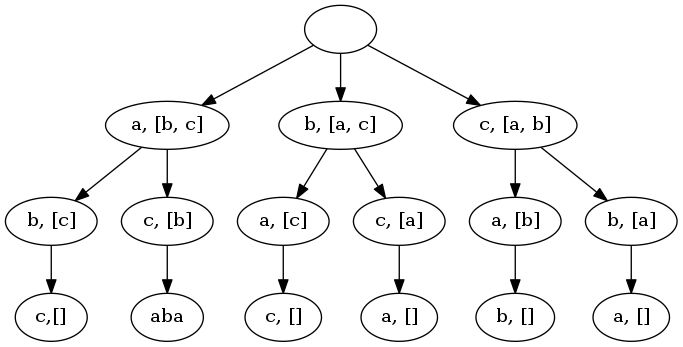
举个例子,给定字符串abc。排列中的第一个元素有三种选择a, b, c。当选择a时,剩余元素为b, c;当选择b时,剩余元素为a, c;当选择c时,剩余元素为a, b。依此类推,当从剩余元素b, c中选取排列中第二个元素时有两种选择b, c。当选择b时,剩余元素c;当选择c时,剩余b。
从根节点到叶子节点的路径即是一种排列。
代码实现
package io.github.rscai.leetcode.bytedance.string;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class Solution1016A {
public boolean checkInclusion(String s1, String s2) {
if(s1.length()>s2.length()){
return false;
}
for (String str : permutation(s1)) {
if (s2.contains(str)) {
return true;
}
}
return false;
}
List<String> permutation(String str) {
if (str.length() == 0) {
return Collections.singletonList("");
}
List<String> permutations = new ArrayList<>();
for (int i = 0; i < str.length(); i++) {
char ch = str.charAt(i);
for (String remain : permutation(strMinusAtIndex(str, i))) {
permutations.add(ch + remain);
}
}
return permutations;
}
private String strMinusAtIndex(String str, int index) {
if (index < 0) {
return str;
}
if (index >= str.length()) {
return str;
}
if (index == str.length() - 1) {
return str.substring(0, index);
}
return str.substring(0, index) + str.substring(index + 1, str.length());
}
}
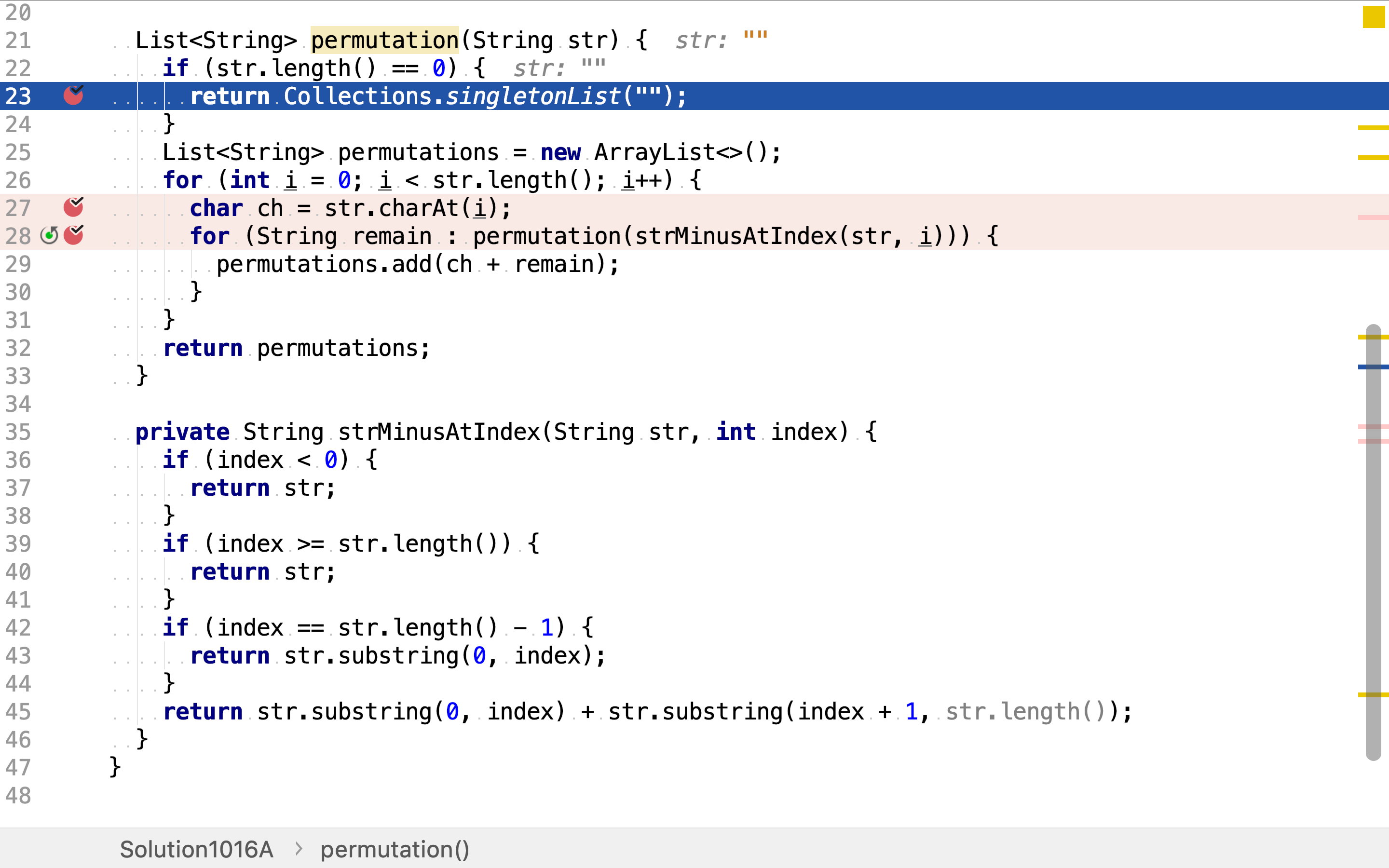
罗列所有排列,再逐一检测是否被第二条字符串包含。
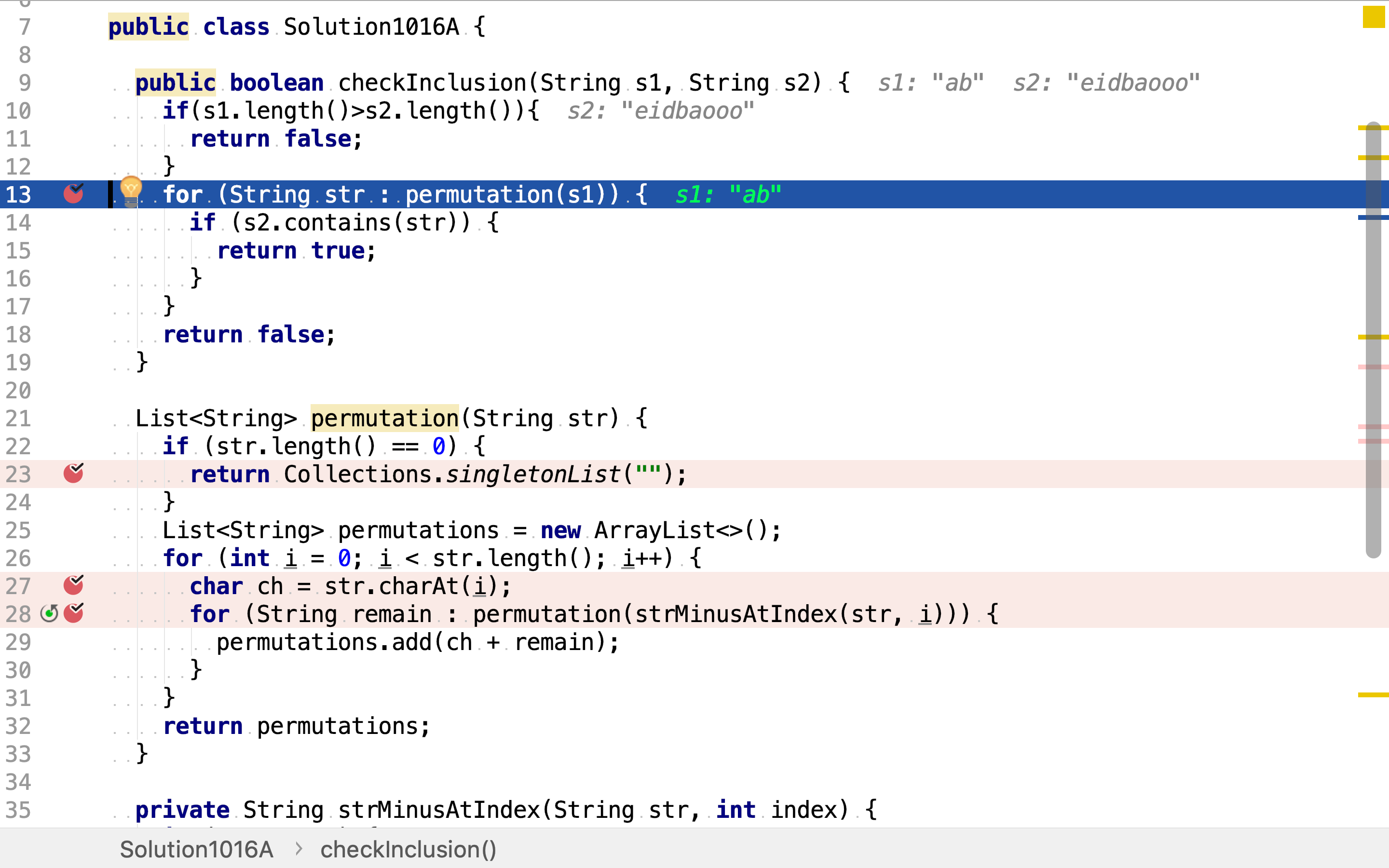
「罗列所有排列」以递归的方式实现。先罗列第一个字符的所有可能,
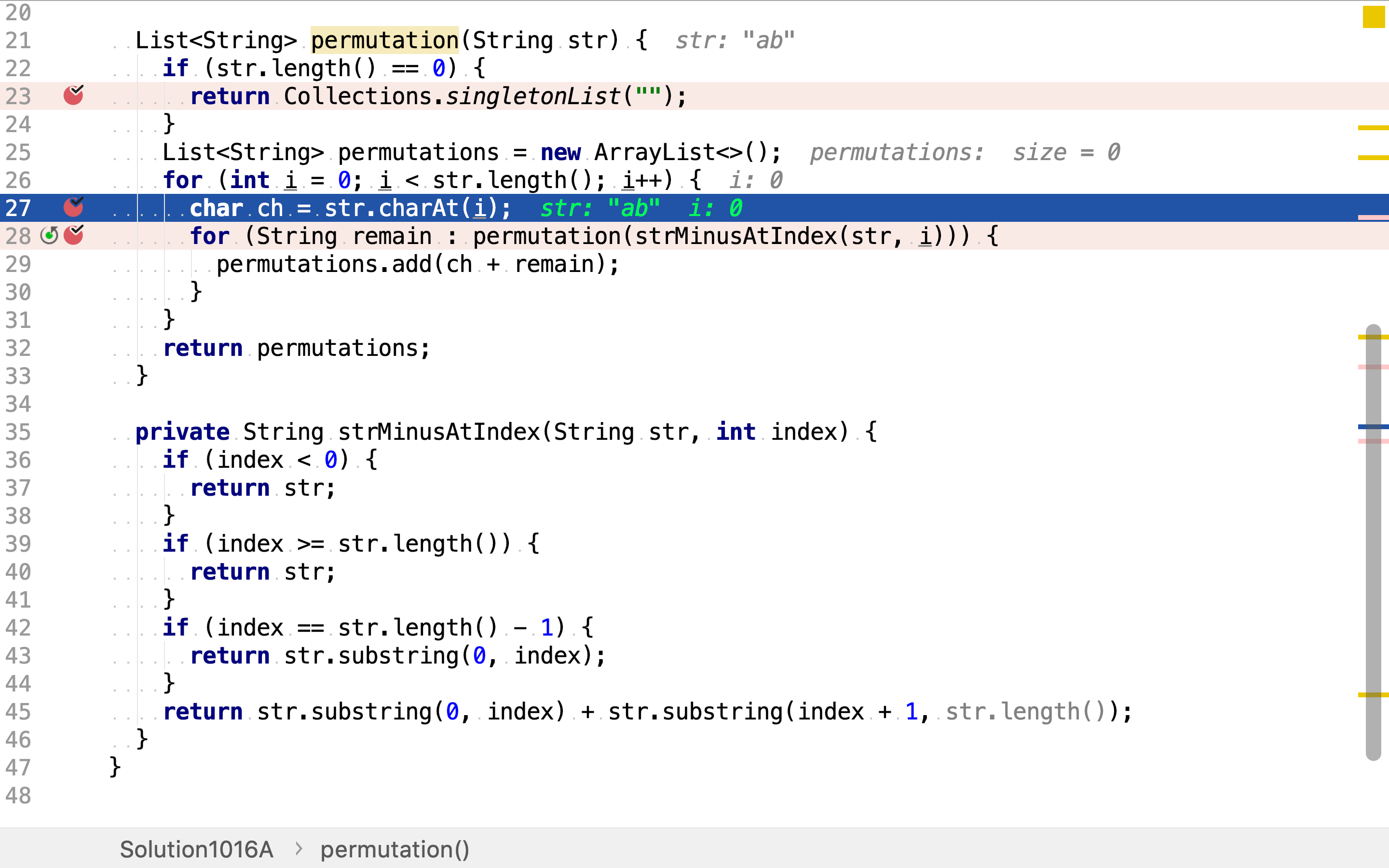
再罗列剩余字符的所有排列,最后再将第一个字符的所有可能和剩余字符所有排列作全组合,就得到所有排列。
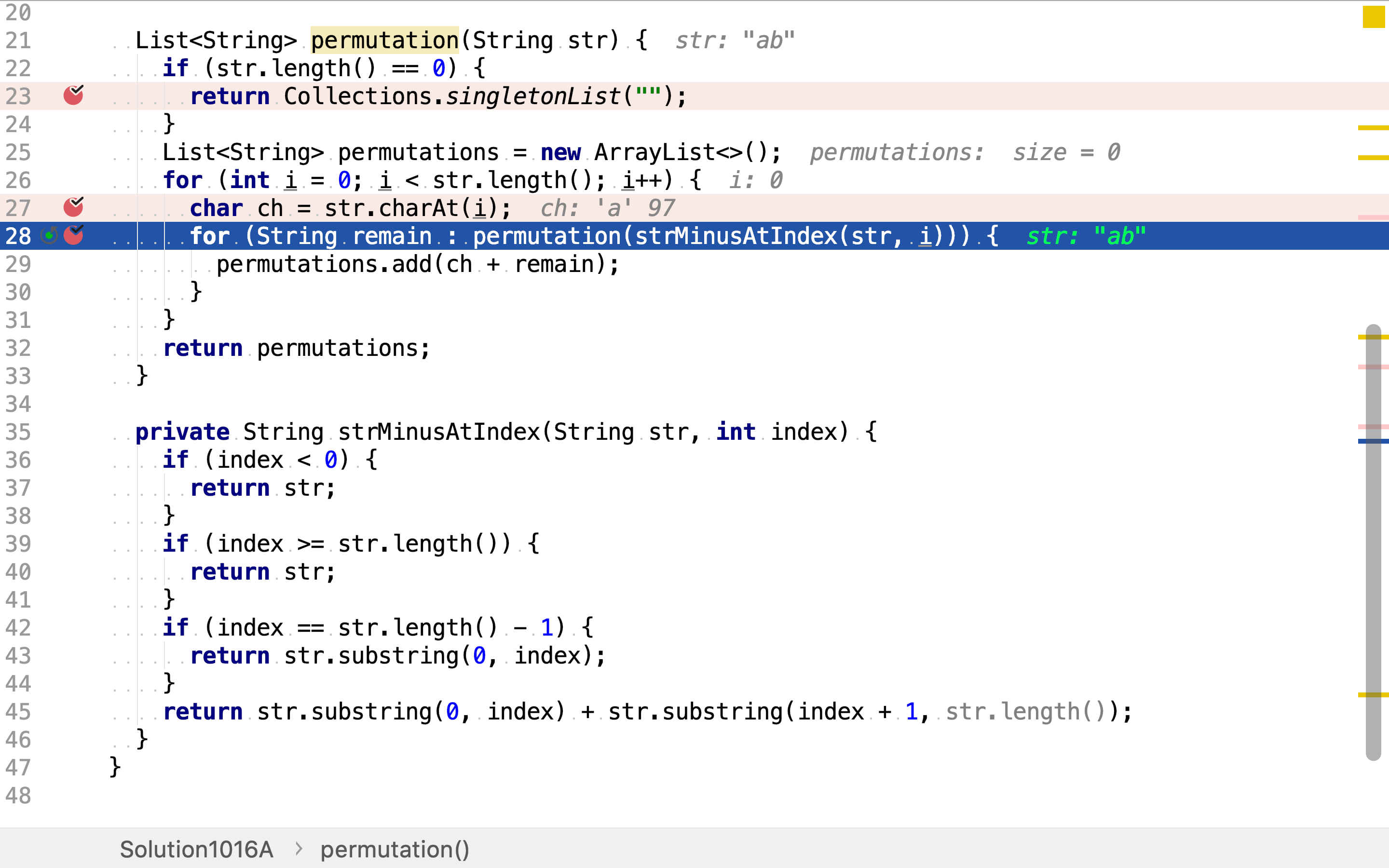
递归终止条件为剩余字符为空。
复杂度分析
时间复杂度
排列数量公式为:
本演算法使用String.contains检测试是否包含,String.contains的时间复杂度为。所以整体时间复杂度为。
空间复杂度
其要先罗列所有排列,再逐一检测。所以空间复杂度为。
回溯法
回溯法
回溯法(英语:backtracking)是暴力搜寻法中的一种。
对于某些计算问题而言,回溯法是一种可以找出所有(或一部分)解的一般性演算法,尤其适用于约束满足问题(在解决约束满足问题时,我们逐步构造更多的候选解,并且在确定某一部分候选解不可能补全成正确解之后放弃继续搜寻这个部分候选解本身及其可以拓展出的子候选解,转而测试其他的部分候选解)。
在经典的教科书中,八皇后问题展示了回溯法的用例。(八皇后问题是在标准西洋棋棋盘中寻找八个皇后的所有分布,使得没有一个皇后能攻击到另外一个。)
回溯法採用试错的思想,它尝试分步的去解决一个问题。在分步解决问题的过程中,当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候,它将取消上一步甚至是上几步的计算,再通过其它的可能的分步解答再次尝试寻找问题的答案。回溯法通常用最简单的递回方法来实现,在反覆重复上述的步骤后可能出现两种情况:
1.找到一个可能存在的正确的答案
2.在尝试了所有可能的分步方法后宣告该问题没有答案
在最坏的情况下,回溯法会导致一次复杂度为指数时间的计算。
回溯法
当一个字符串不包含另一个字符串时,以别一个字符串为前缀的任意字符串都不被该字符所包含。
举个例子,给定字符串abc。假如另一个字符串S不包含a,则其一定不包含以a开始任何字串。也就是说,在罗列排列时,如点发现目标字符串不包含排列的开始部份,则无需再罗列或检测其余拥有相同开始部份的排列。

代码实现
package io.github.rscai.leetcode.bytedance.string;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class Solution1016B {
public boolean checkInclusion(String s1, String s2) {
if (s1.length() > s2.length()) {
return false;
}
Object[] result = permutation(s1, "", s2);
return (Boolean) result[0];
}
Object[] permutation(String str, String accessed, String target) {
if (str.length() == 0) {
return new Object[]{true, Collections.singletonList("")};
}
List<String> permutations = new ArrayList<>();
for (int i = 0; i < str.length(); i++) {
char ch = str.charAt(i);
if (target.contains(accessed + ch)) {
Object[] remain = permutation(strMinusAtIndex(str, i), accessed + ch, target);
boolean isNil = (Boolean) remain[0];
if (isNil) {
return new Object[]{true, Collections.emptyList()};
}
List<String> remainPermutations = (List<String>) remain[1];
for (String remainPermutation : remainPermutations) {
permutations.add(ch + remainPermutation);
}
}
}
return new Object[]{false, permutations};
}
private String strMinusAtIndex(String str, int index) {
if (index < 0) {
return str;
}
if (index >= str.length()) {
return str;
}
if (index == str.length() - 1) {
return str.substring(0, index);
}
return str.substring(0, index) + str.substring(index + 1, str.length());
}
}
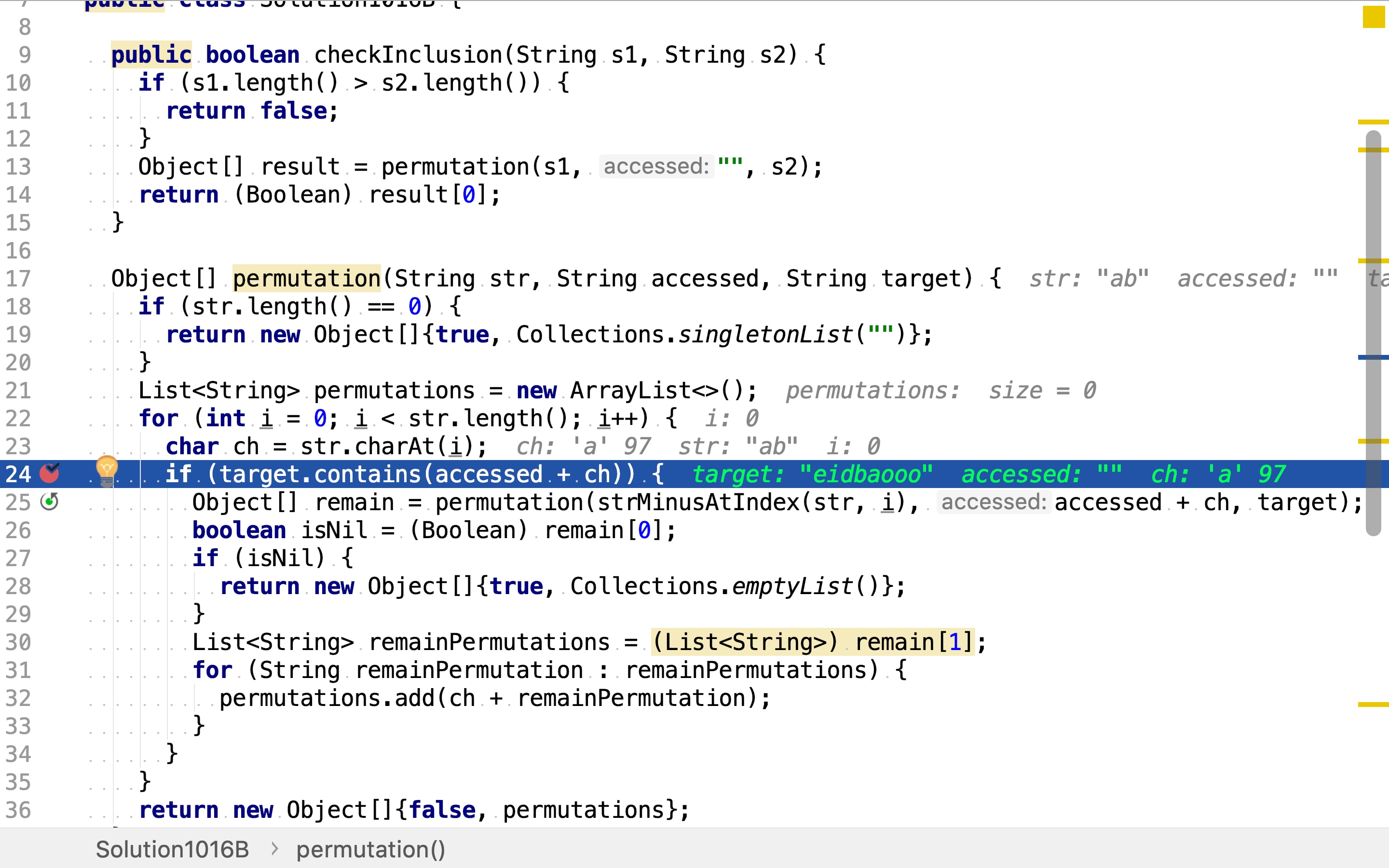
回溯法与枚举法大体相同,只是在每一个节点探索时都判断从根至当前节点的路径构成的部份解是否违反条件约束。若部份解已违返约束,则无需再探索由此部份解组成的其余完整解了。
字符数量比较法
重新审题,「s2包含s1的任一排列」可以转换为「s2的任一子串与s1包含相同字符集合相同且每个字符出现的次数也相同」。若要两个字符串包含字符集合相同且字符出现的次数相同,则两个字符串长度必相同。所以,问题就转化为:s2是否包含长度等于s1的长度,且字符集合与s1相同,且字符出现次数与s1相同。
至此,只需要罗列s2中长度与s1相同的子串,计算子串和s1中字符出现次数并比较。
罗列一个字符串所有指定长度的子串其实就是罗列子串开始位罝。假设字符串长度为m,子串长度为n,则子串数量为m-n+1。
举个例子,给定s1ab,s2eidbaooo。则s2长度为2的子串为:
代码实现
package io.github.rscai.leetcode.bytedance.string;
public class Solution1016C {
public boolean checkInclusion(String s1, String s2) {
if (s1.length() > s2.length()) {
return false;
}
int[] s1LetterCounts = strToCounts(s1);
for (int start = 0; start <= s2.length() - s1.length(); start++) {
String sub = s2.substring(start, start + s1.length());
int[] subLetterCounts = strToCounts(sub);
if (isEqual(s1LetterCounts, subLetterCounts)) {
return true;
}
}
return false;
}
private int[] strToCounts(String str) {
int[] counts = new int[26];
for (int i = 0; i < str.length(); i++) {
int index = Character.codePointAt(str, i) - 97;
counts[index] = counts[index] + 1;
}
return counts;
}
private boolean isEqual(int[] a, int[] b) {
if (a.length != b.length) {
return false;
}
for (int i = 0; i < a.length; i++) {
if (a[i] != b[i]) {
return false;
}
}
return true;
}
}
计算s1中字符出现次数。
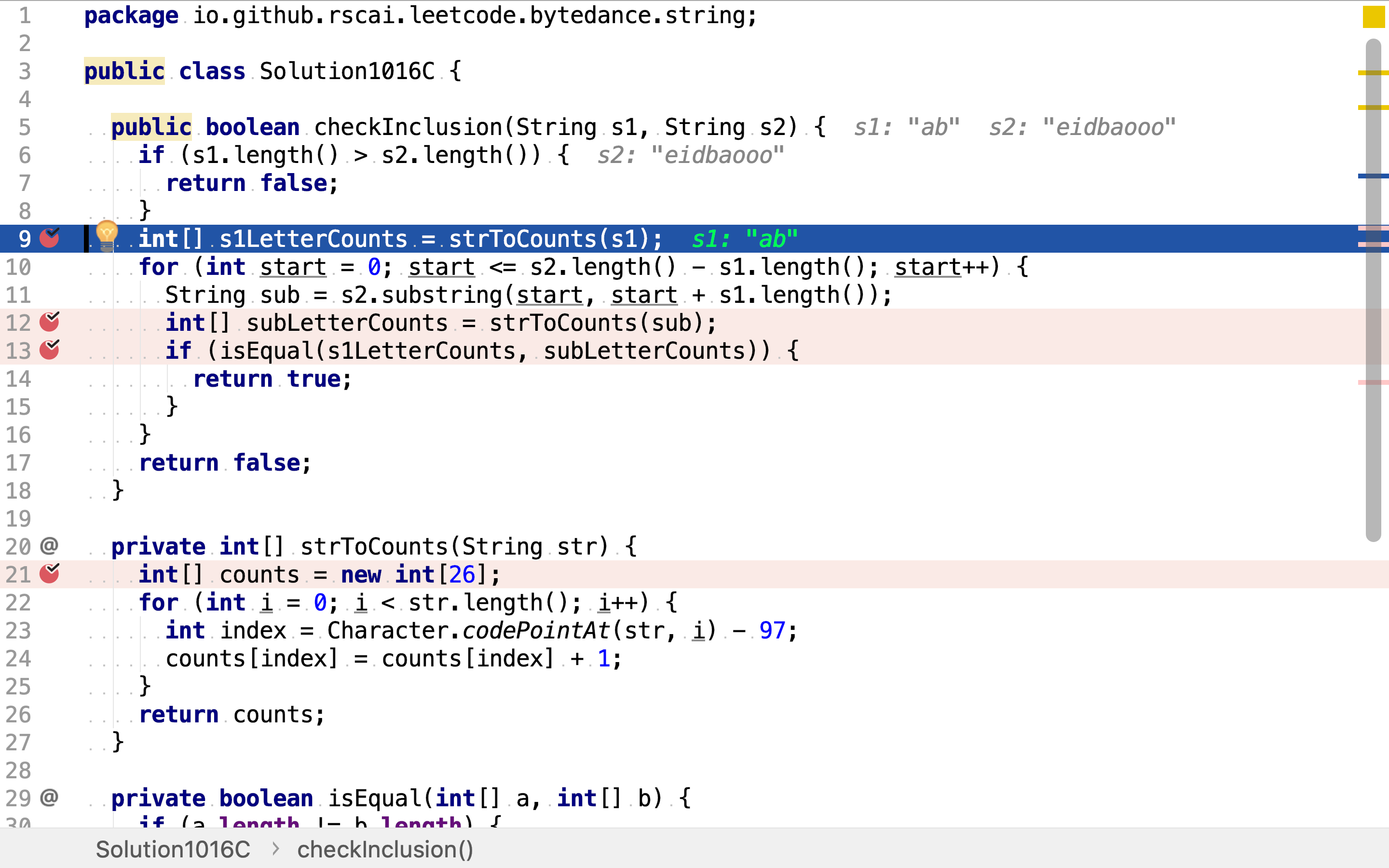
然后,罗列所有长度等于s1的子串,并计算字符出现次数。
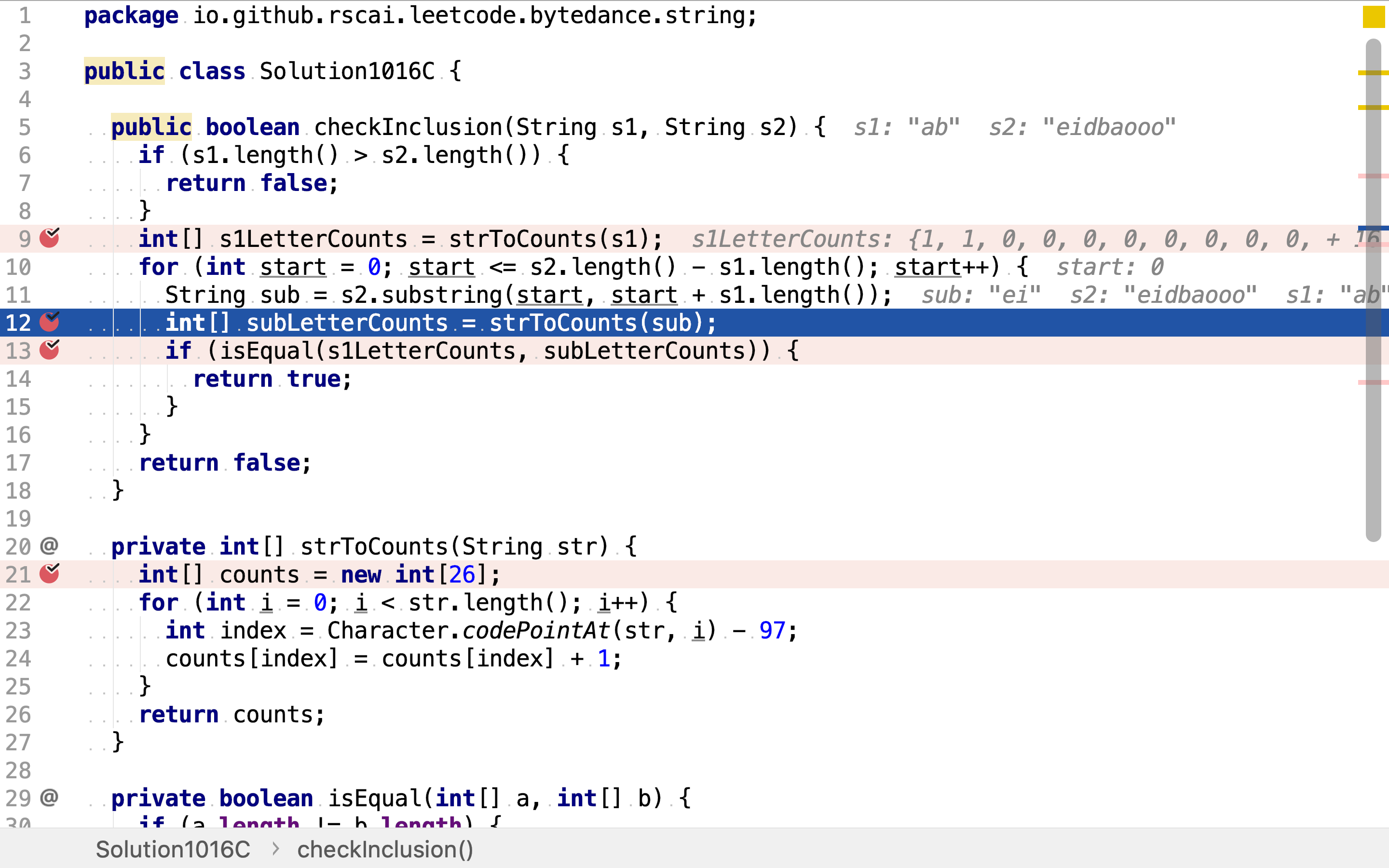
最后,比较s1与子串字符出现次数是否相同。若字符出现次数相同,则一定能排列出相同的字符串。
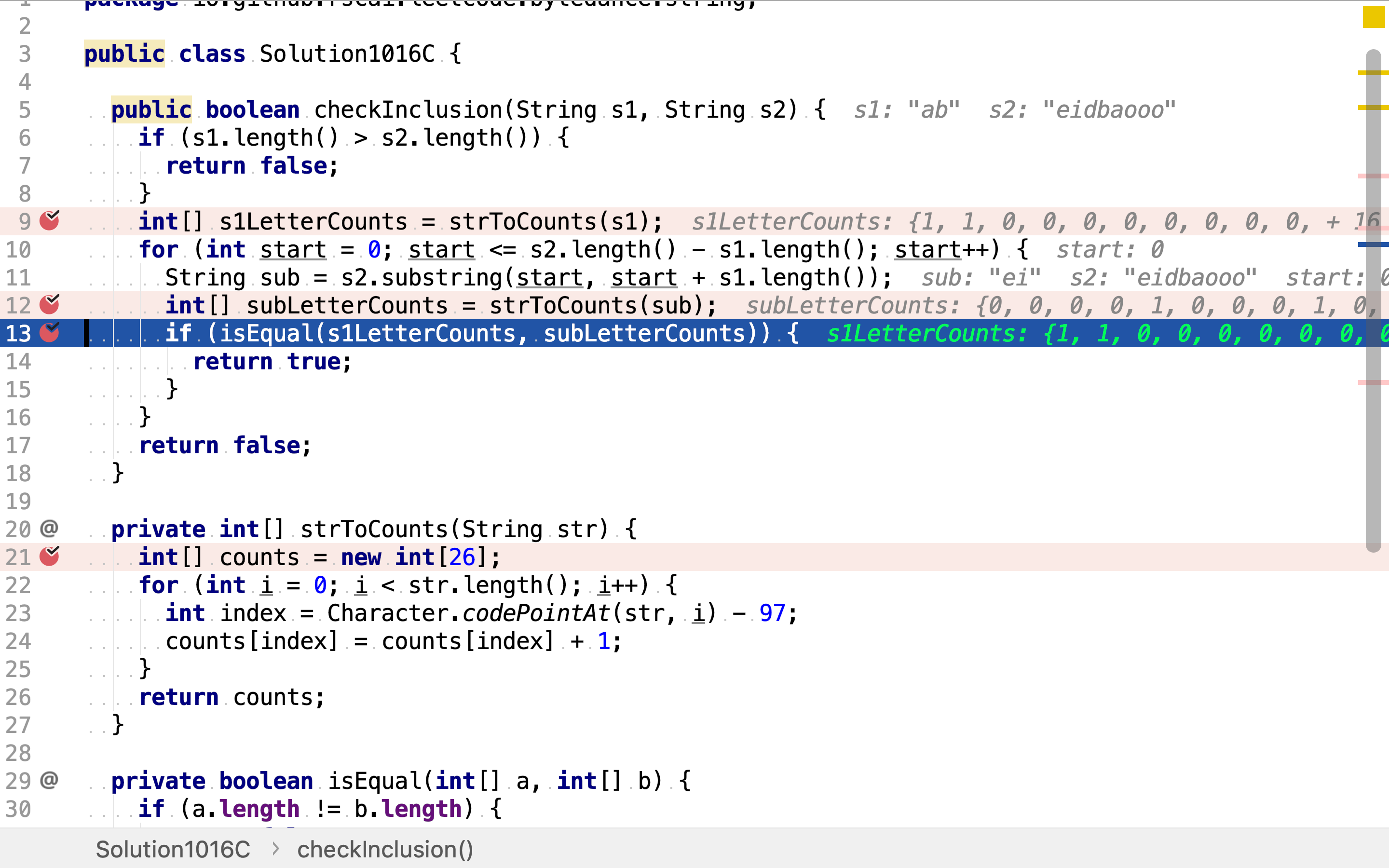
小写英文字母的ANSII或UNICODE编码都是连续的,所以可以用连续的长度为26的数组存储字符出现次数。
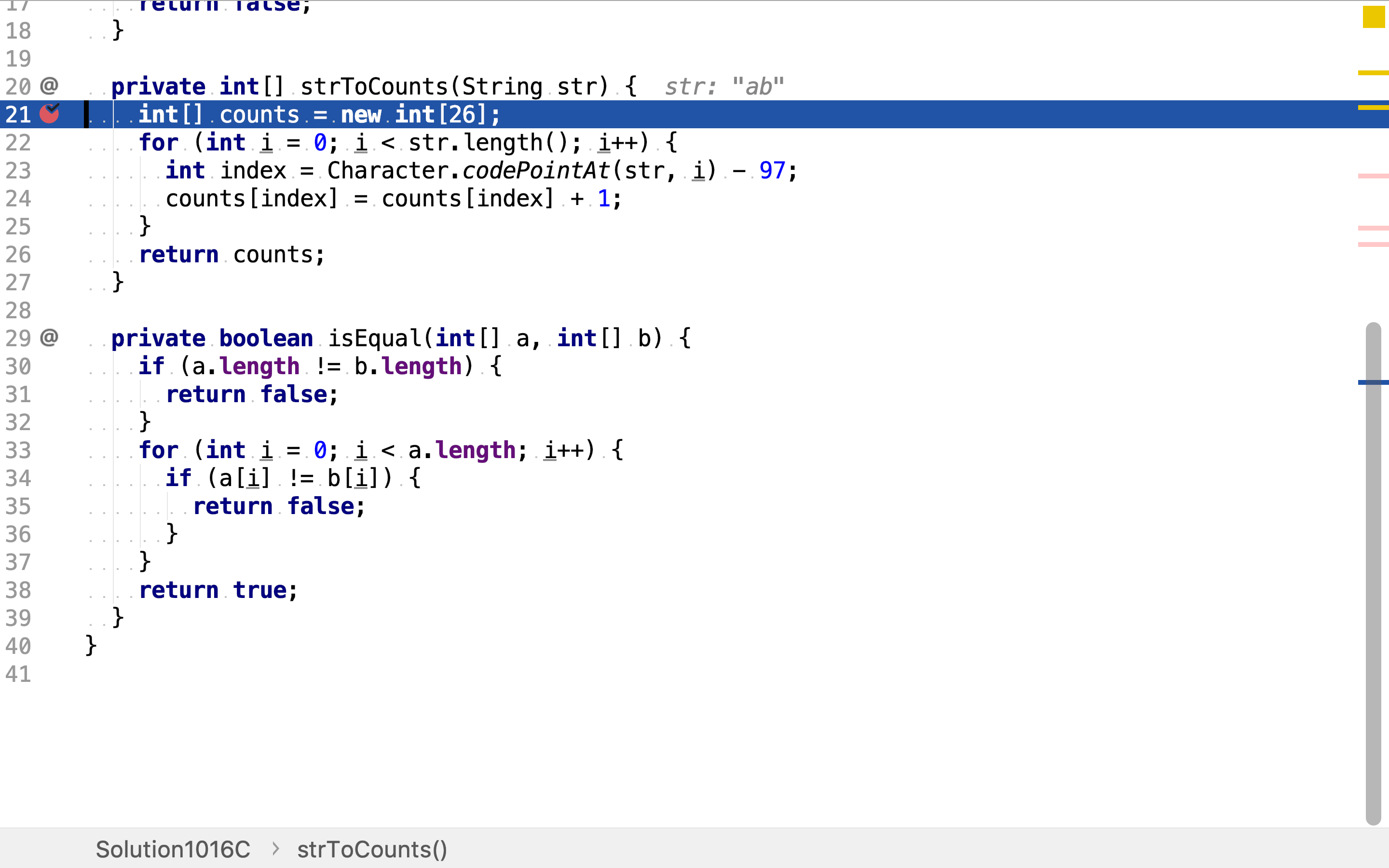
复杂度分析
时间复杂度
假设s1长度为m,s2长度为n。s2中长度为m的子串数量为n-m+1。
空间复杂度
使用了两个长度为26的数组s1LetterCounts, subLetterCounts和长度为s1长度的sub。空间复杂度为。
滑动窗口
上述「字符数量比较法」中,s2中长度跟s1相等的子串,相邻的相差仅有两个字符。所以,在计算子串中字符出现次数时,无需遍历整个子串,而仅需在前一个子串的字符出现次数结果中加减各一次。
举个例子,给定s1ab,s2eidbaooo。则s2长度为2的子串为:
假设已得到子串ei的字符出现次数字典mapA,下一个子串id相较与ei,减少了一个e且增加了一个d。以mapA为基础,将e的计数减一,将d的计数加一,即得到了子串id的字符出现次数字典mapB。依此类推,子串db的出现次数字典可以在mapB的基础上,将i计数减一,将b计数加一得到。
代码实现
package io.github.rscai.leetcode.bytedance.string;
public class Solution1016D {
private static final int CHAR_CODE_OFFSET = 97;
public boolean checkInclusion(String s1, String s2) {
if (s1.length() > s2.length()) {
return false;
}
int[] s1LetterCounts = strToCounts(s1);
String sub = s2.substring(0, s1.length());
int[] subLetterCounts = strToCounts(sub);
if (isEqual(s1LetterCounts, subLetterCounts)) {
return true;
}
for (int start = 1; start <= s2.length() - s1.length(); start++) {
char removedChar = s2.charAt(start - 1);
char addedChar = s2.charAt(start + s1.length() - 1);
subLetterCounts[removedChar - CHAR_CODE_OFFSET] =
subLetterCounts[removedChar - CHAR_CODE_OFFSET] - 1;
subLetterCounts[addedChar - CHAR_CODE_OFFSET] =
subLetterCounts[addedChar - CHAR_CODE_OFFSET] + 1;
if (isEqual(s1LetterCounts, subLetterCounts)) {
return true;
}
}
return false;
}
private int[] strToCounts(String str) {
int[] counts = new int[26];
for (int i = 0; i < str.length(); i++) {
int index = Character.codePointAt(str, i) - CHAR_CODE_OFFSET;
counts[index] = counts[index] + 1;
}
return counts;
}
private boolean isEqual(int[] a, int[] b) {
if (a.length != b.length) {
return false;
}
for (int i = 0; i < a.length; i++) {
if (a[i] != b[i]) {
return false;
}
}
return true;
}
}
先计算第一个子串中字符出现次数,并比较是否与s1的相同。
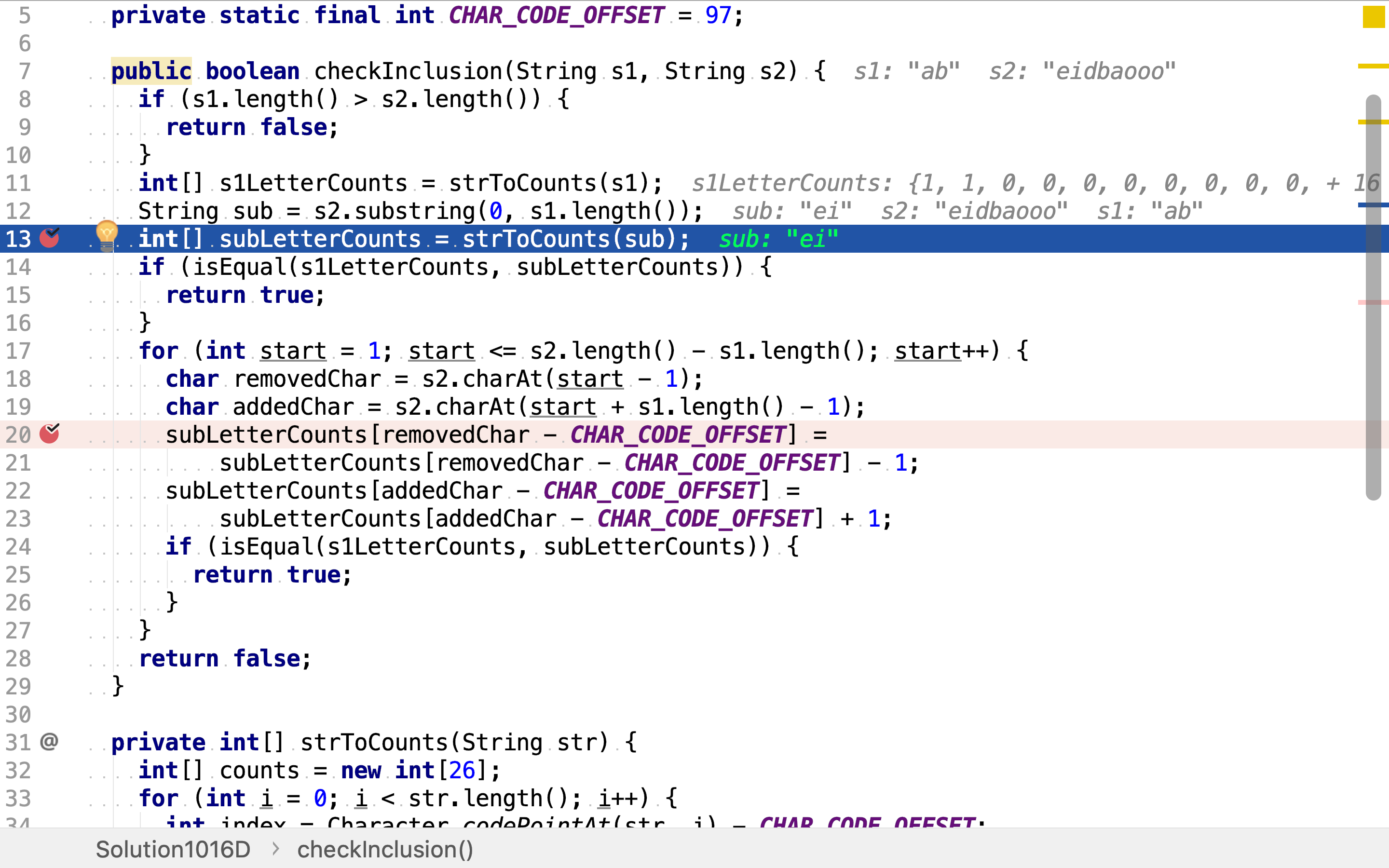
再依次以消减一个字符计数和增加一个字符计数的方式计算后续子串的字符出现次数,并比较是否与s1的相同。
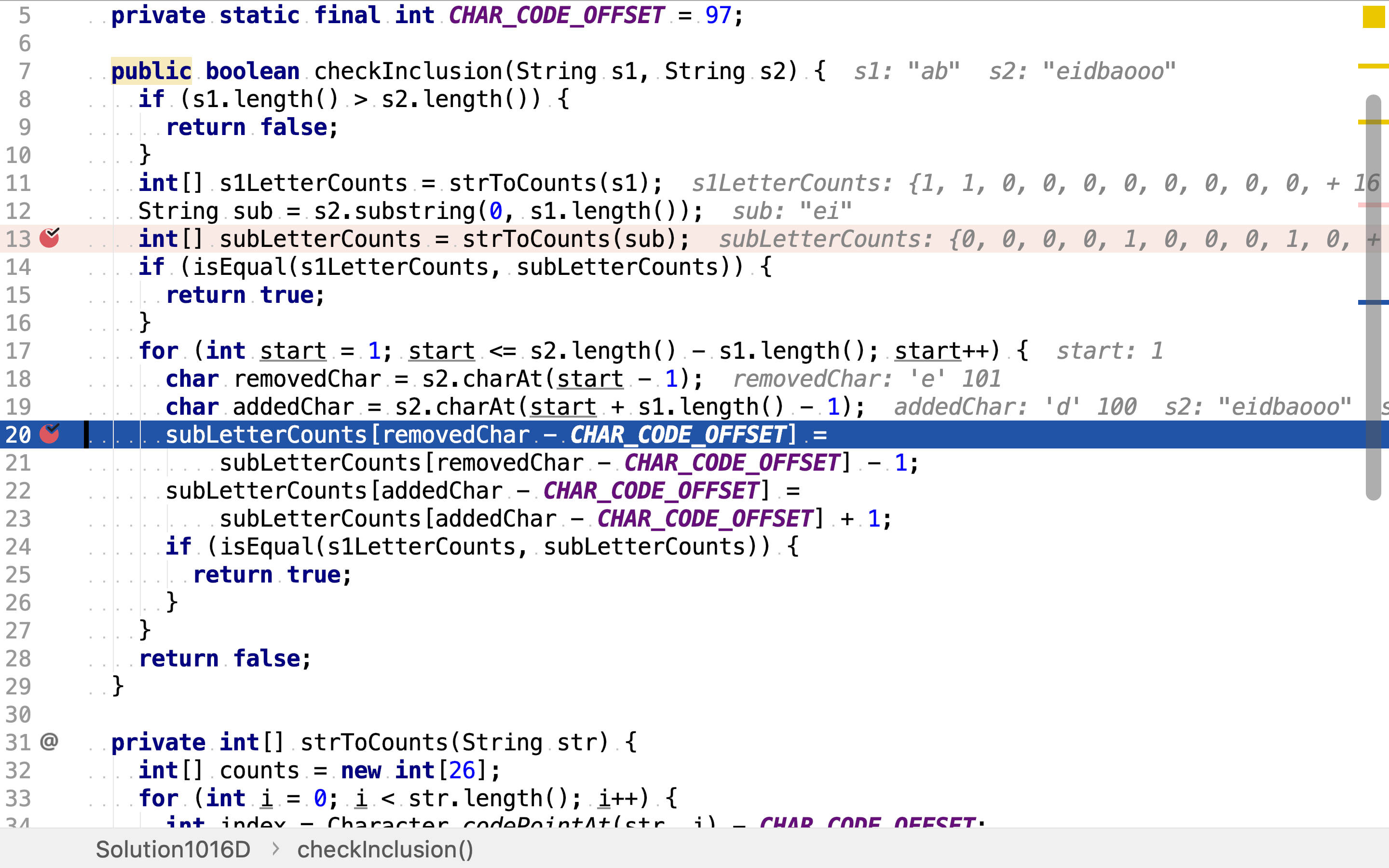
复杂度分析
时间复杂度
本演算法只遍历了第一个子串,求得字符出现次数。其余子串的字符出现次数都是通过一次加、一次减求得的。所以时间复杂度为。
空间复杂度
与上述「字符数量比较法」相同,为。












