二叉树的锯齿形层次遍历
题目
给定一个二叉树,返回其节点值的锯齿形层次遍历。 (即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
例如: 给定二叉树 [3,9,20,null,null,15,7],
3 / \ 9 20 / \ 15 7返回锯齿形层次遍历如下:
[ [3], [20,9], [15,7] ]
依深度定位方向
二叉树中每一行节点遍历方向可由其在二叉树中的深度直接确定。根节点的深度计为0,每往下一层深度加一。当深度为偶数时(0在此当作偶数)节点遍历顺序为从左往右,当深度为奇数时节点遍历顺序为从右往左。
举个例子,给定如下二叉树:
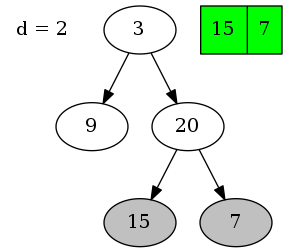
先自上而下遍历到底部,再从下而上归併。最底层的深度为2,这一层的节点需从左往右遍历。
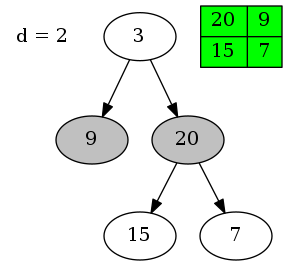
往上一层深度为1,这一层的节点需从右往左遍历。
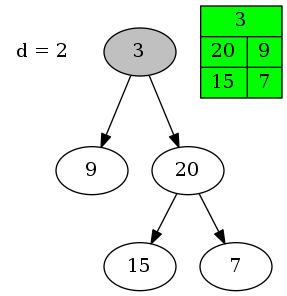
再往上一层深度为0,这一层的节点需从左往右遍历。
代码
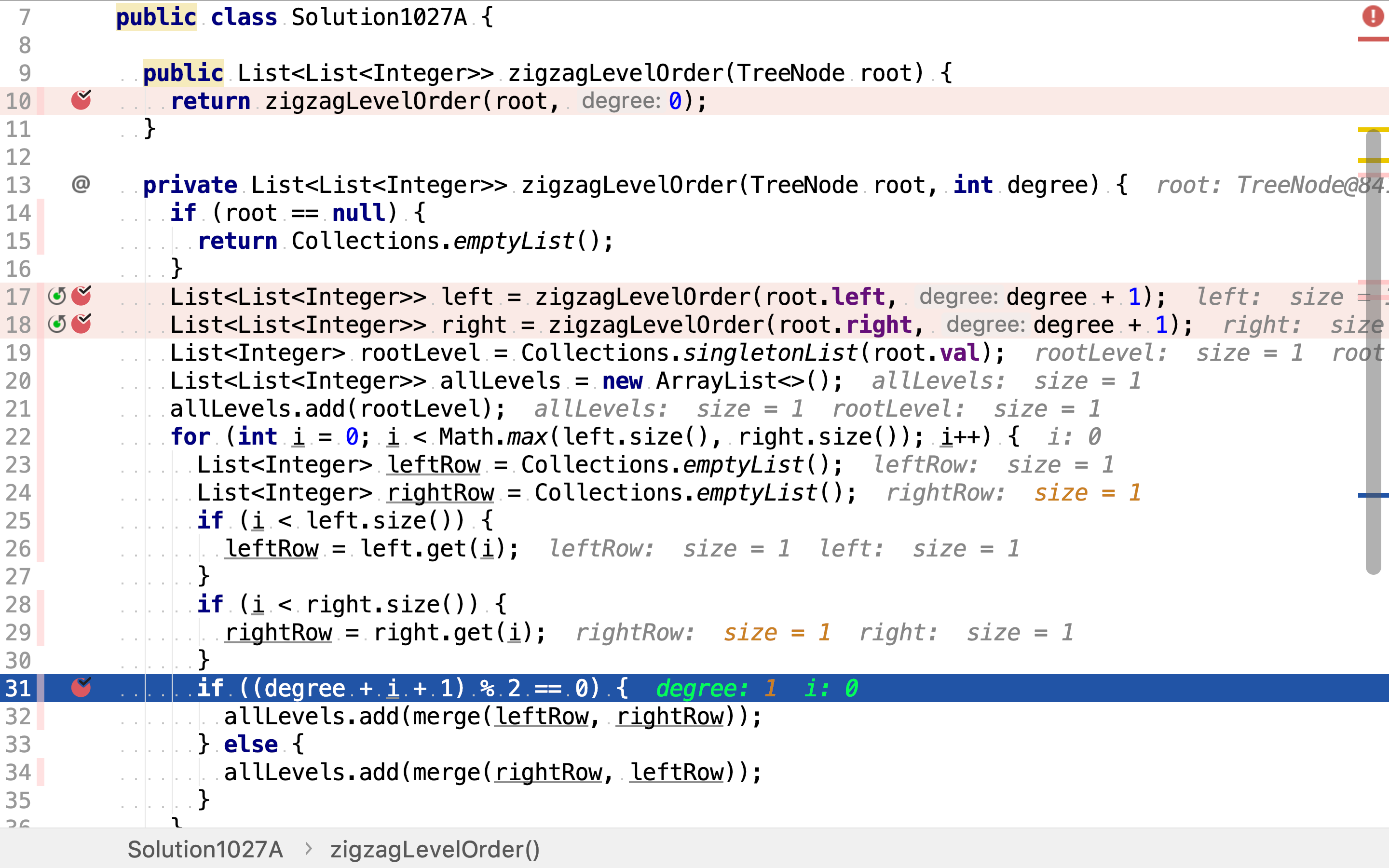
package io.github.rscai.leetcode.bytedance.linktree;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class Solution1027A {
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
return zigzagLevelOrder(root, 0);
}
private List<List<Integer>> zigzagLevelOrder(TreeNode root, int degree) {
if (root == null) {
return Collections.emptyList();
}
List<List<Integer>> left = zigzagLevelOrder(root.left, degree + 1);
List<List<Integer>> right = zigzagLevelOrder(root.right, degree + 1);
List<Integer> rootLevel = Collections.singletonList(root.val);
List<List<Integer>> allLevels = new ArrayList<>();
allLevels.add(rootLevel);
for (int i = 0; i < Math.max(left.size(), right.size()); i++) {
List<Integer> leftRow = Collections.emptyList();
List<Integer> rightRow = Collections.emptyList();
if (i < left.size()) {
leftRow = left.get(i);
}
if (i < right.size()) {
rightRow = right.get(i);
}
if ((degree + i + 1) % 2 == 0) {
allLevels.add(merge(leftRow, rightRow));
} else {
allLevels.add(merge(rightRow, leftRow));
}
}
return allLevels;
}
private List<Integer> merge(List<Integer> first, List<Integer> second) {
List<Integer> result = new ArrayList<>(first.size() + second.size());
result.addAll(first);
result.addAll(second);
return result;
}
}
将深度作为参数在递归函数之间传递。在归併结果的时候,就能通过深度确定合併子问题结果的方向(从左往右/从右往左)。
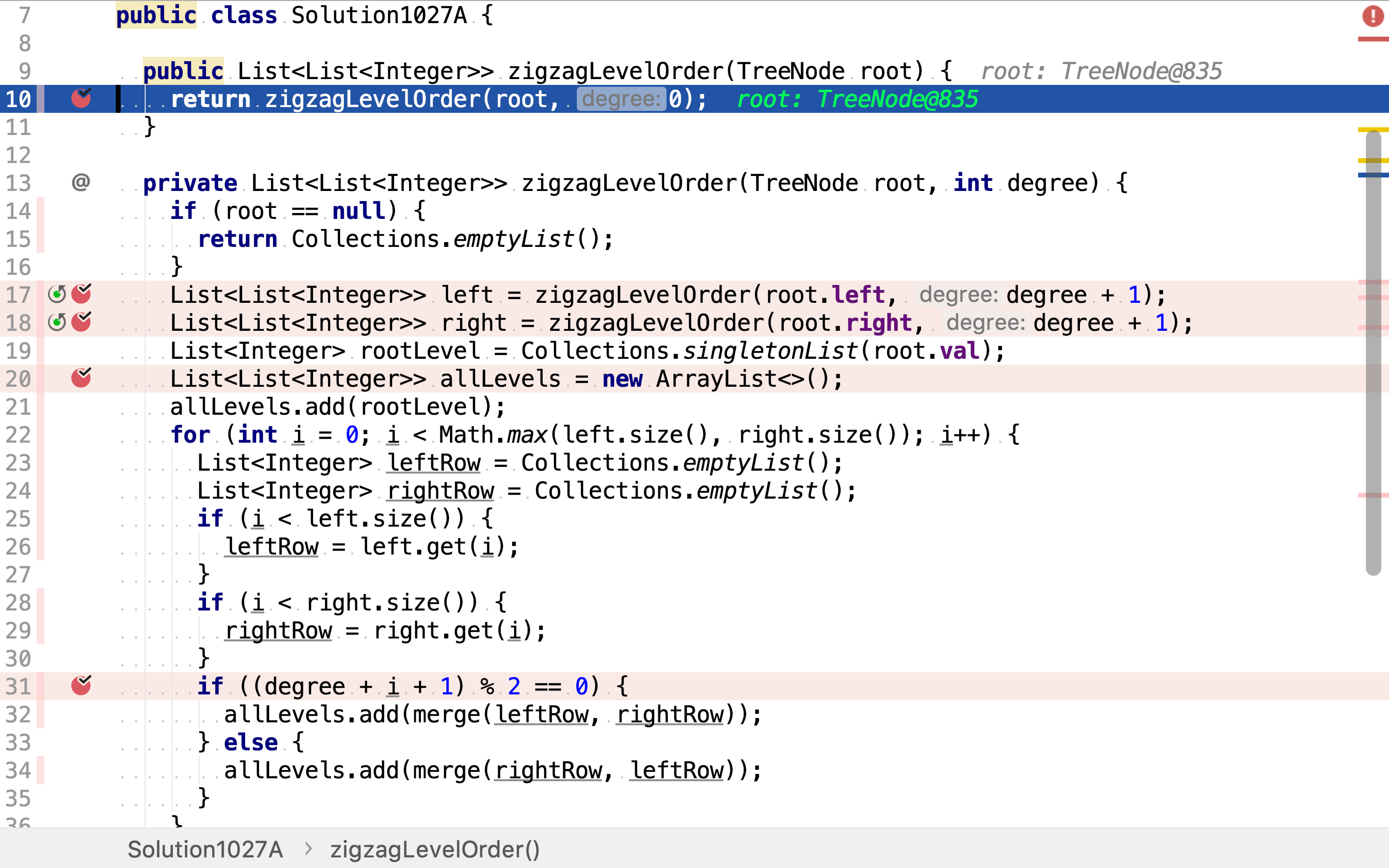
先递回遍历左子树,
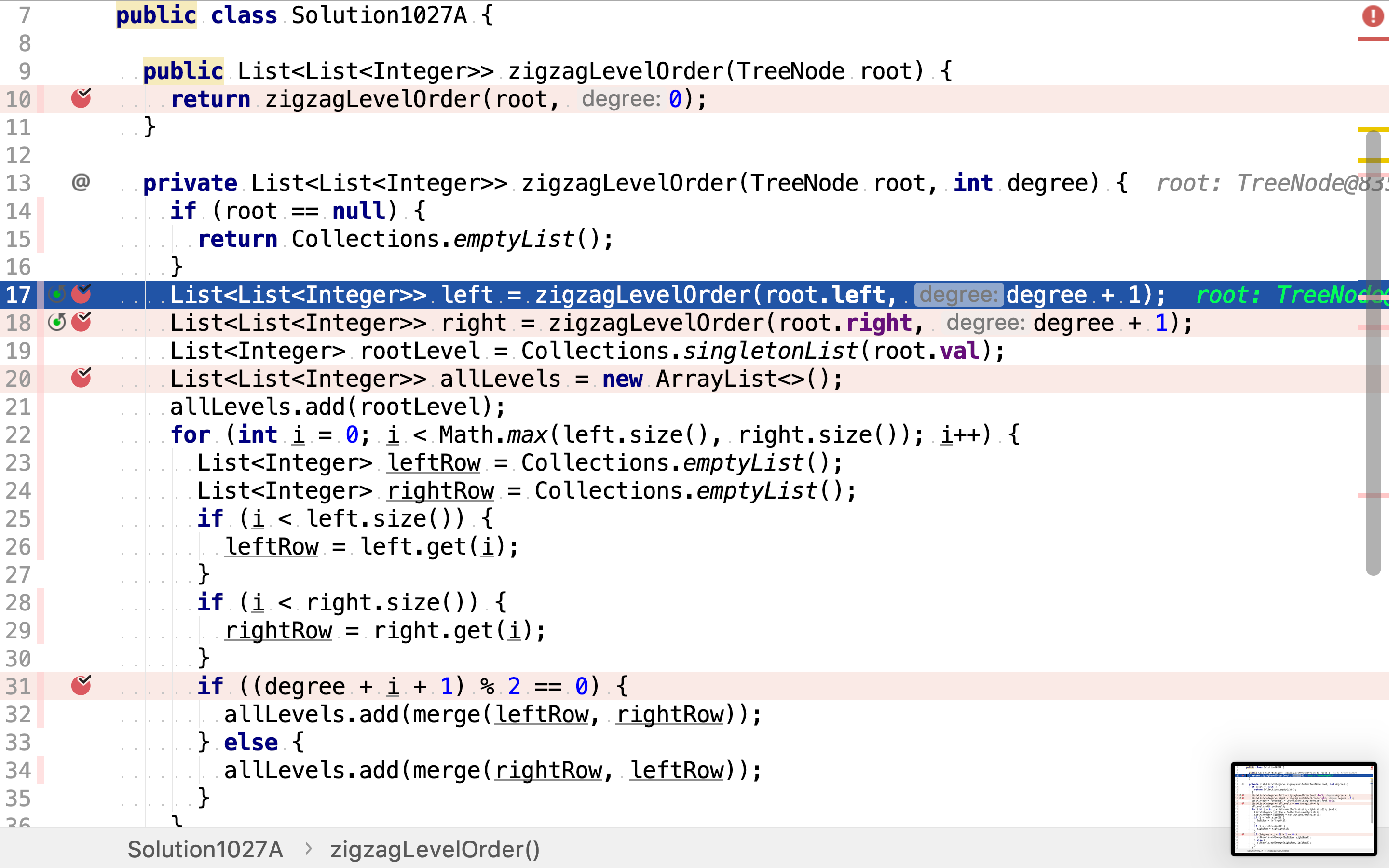
再递回遍历右子树。
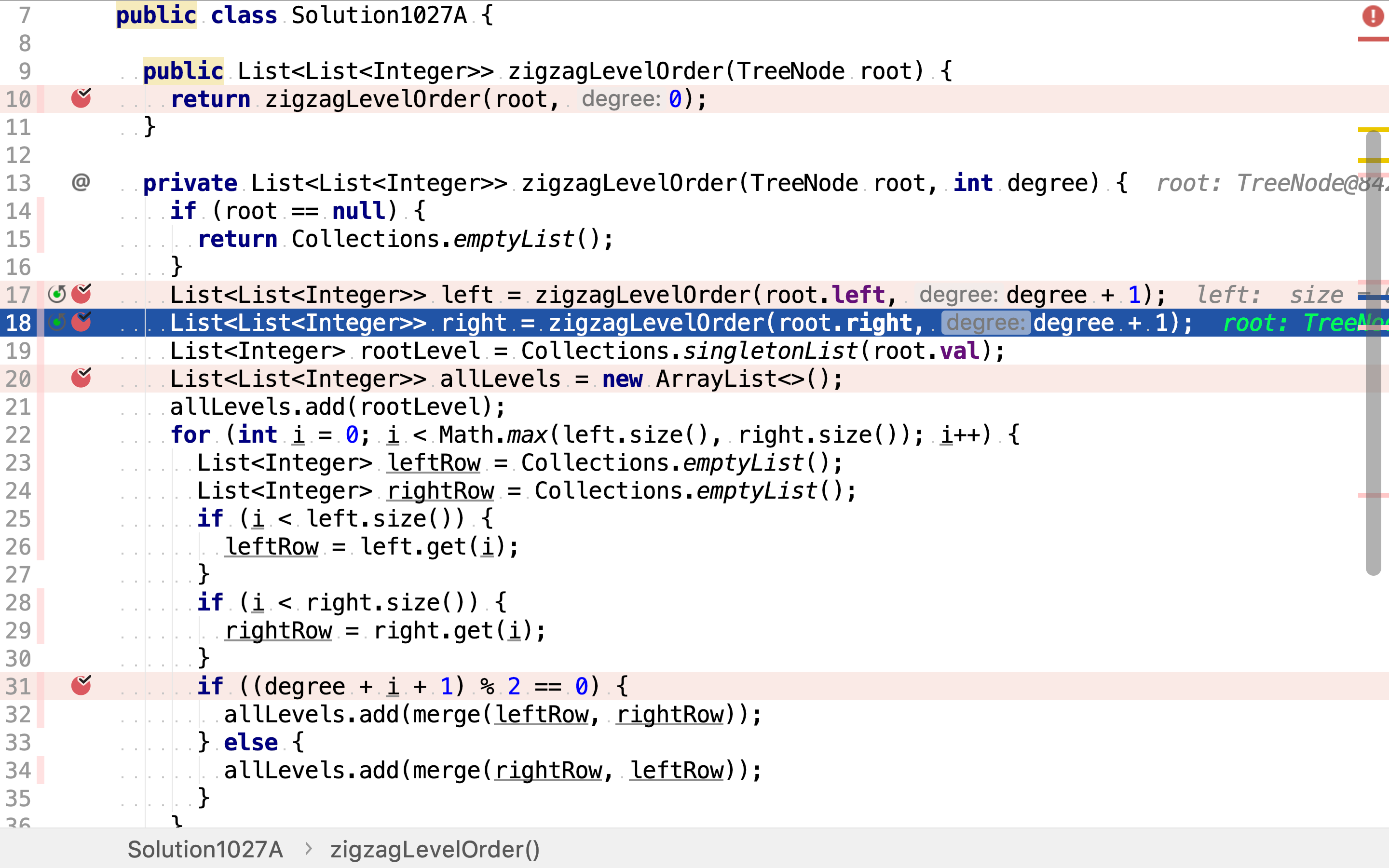
归併结果时,根节点层只有一个节点,无论以什么方向遍历,结果都一样。
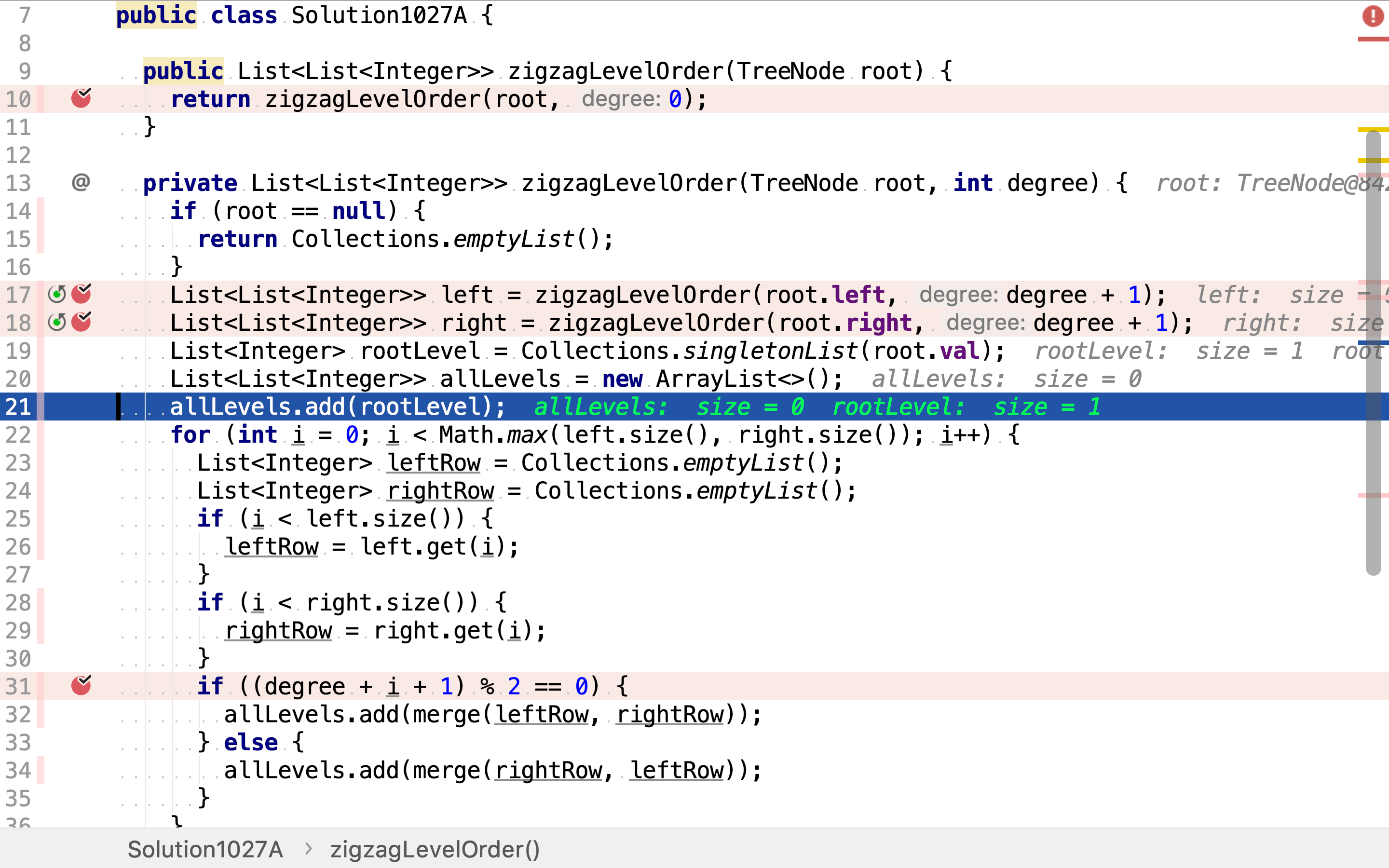
左右子树的结果则需按深度确定方向。根节点的深度加其在子树中的深度再加一(子树中的相对深度也是从0开始计的)。深度为偶数,则从左往右归併结果;若深度为奇数,则从右往左归併结果。
复杂度分析
时间复杂度
本演算法遍历了二叉树一次,时间复杂度为。
空间复杂度
解中包含了二叉树中所有的节点,所以空间复杂度为。