排序链表
题目
在 O(n log n) 时间复杂度和常数级空间复杂度下,对链表进行排序。
示例:
输入: 4->2->1->3
输出: 1->2->3->4
示例:
输入: -1->5->3->4->0
输出: -1->0->3->4->5
合併排序
合併排序(英语:Merge sort,或mergesort),是建立在合併操作上的一种有效的排序演算法,效率为 (大O符号)。1945年由约翰·冯·纽曼首次提出。该演算法是採用分治法(Divide and Conquer)的一个非常典型的应用,且各层分治递回可以同时进行。
概述
採用分治法:
- 分割:递回地把目前序列平均分割成两半。
- 整合:在保持元素顺序的同时将上一步得到的子序列整合到一起(合併)。
合併操作
合併操作(merge),也叫合併演算法,指的是将两个已经排序的序列合併成一个序列的操作。合併排序演算法依赖合併操作。
递回法(Top-down)
- 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合併后的序列
- 设定两个指标,最初位置分别为两个已经排序序列的起始位置
- 比较两个指标所指向的元素,选择相对小的元素放入到合併空间,并移动指标到下一位置
- 重复步骤3直到某一指标到达序列尾
- 将另一序列剩下的所有元素直接复制到合併序列尾
叠代法(Bottom-up)
原理如下(假设序列共有个元素):
- 将序列每相邻两个数字进行合併操作,形成 个序列,排序后每个序列包含两/一个元素
- 若此时序列数不是1个则将上述序列再次合併,形成个序列,每个序列包含四/三个元素
- 重复步骤2,直到所有元素排序完毕,即序列数为1
举个例子,给定链表4->2->1->3。首先,递回地将链表分割为两半,直到链表长度为1。
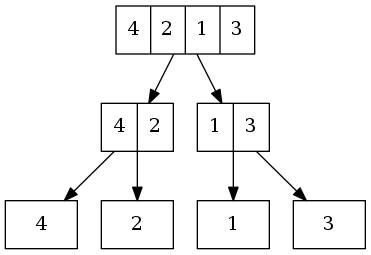
再使用叠代法自下而上合併。每两个链表向上合併成一个链表。
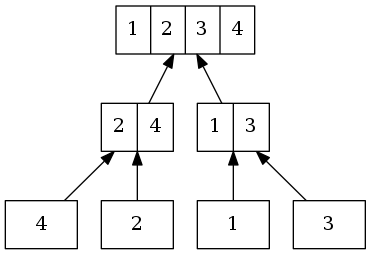
合併步骤:
- 先从候选链表头元素中取出最小的一个放入新链表,被选中的链表头元素引用向后移一位。
- 重复步骤1直至两个链表都到达末尾。
以合併2->4和1->3为例。
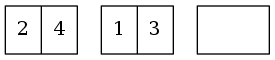
比较两个链表的头元素,1小于2。将1加入新链表,并将头引用后移一位。

比较两个链表的头元素,2小于3。将2`加入新链表,并将头引用后移一位。

比较两个链表的头元素,3小于4。将3加入新链表,并将头引用后移一位。

比较两个链表的头元素,其中一个链表已空。将另一个链表的头元素4加入新链表,并将头引用后移一位。
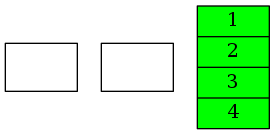
两个链表都已空,合併完成。
代码
package io.github.rscai.leetcode.bytedance.linktree;
/**
* Merge sort
*/
public class Solution1040A {
public ListNode sortList(ListNode head) {
int length = 0;
ListNode current = head;
while (current != null) {
length++;
current = current.next;
}
return mergeSort(head, length);
}
private ListNode mergeSort(ListNode head, int length) {
if (length == 0) {
return head;
}
if (length == 1) {
return head;
}
Object[] headLengths = binarySplit(head, length);
ListNode firstHead = (ListNode) headLengths[0];
int firstLength = (Integer) headLengths[1];
ListNode secondHead = (ListNode) headLengths[2];
int secondLength = (Integer) headLengths[3];
ListNode sortedFirst = mergeSort(firstHead, firstLength);
ListNode sortedSecond = mergeSort(secondHead, secondLength);
return merge(sortedFirst, sortedSecond);
}
private Object[] binarySplit(ListNode head, int length) {
int firstLength = Math.round(length / 2.0F);
int secondLength = length - firstLength;
ListNode secondHead = head;
ListNode firstTail = head;
for (int i = 0; i < firstLength; i++) {
firstTail = secondHead;
secondHead = secondHead.next;
}
firstTail.next = null;
return new Object[]{head, firstLength, secondHead, secondLength};
}
private ListNode merge(ListNode firstHead, ListNode secondHead) {
ListNode mergedHead = null;
ListNode mergedTail = null;
ListNode firstCurrent = firstHead;
ListNode secondCurrent = secondHead;
while (firstCurrent != null || secondCurrent != null) {
if (firstCurrent == null) {
ListNode secondNext = secondCurrent.next;
secondCurrent.next = null;
ListNode[] headAndTail = append(mergedHead, mergedTail, secondCurrent);
mergedHead = headAndTail[0];
mergedTail = headAndTail[1];
secondCurrent = secondNext;
} else if (secondCurrent == null) {
ListNode firstNext = firstCurrent.next;
firstCurrent.next = null;
ListNode[] headAndTail = append(mergedHead, mergedTail, firstCurrent);
mergedHead = headAndTail[0];
mergedTail = headAndTail[1];
firstCurrent = firstNext;
} else if (firstCurrent.val < secondCurrent.val) {
ListNode firstNext = firstCurrent.next;
firstCurrent.next = null;
ListNode[] headAndTail = append(mergedHead, mergedTail, firstCurrent);
mergedHead = headAndTail[0];
mergedTail = headAndTail[1];
firstCurrent = firstNext;
} else {
ListNode secondNext = secondCurrent.next;
secondCurrent.next = null;
ListNode[] headAndTail = append(mergedHead, mergedTail, secondCurrent);
mergedHead = headAndTail[0];
mergedTail = headAndTail[1];
secondCurrent = secondNext;
}
}
return mergedHead;
}
private ListNode[] append(ListNode head, ListNode tail, ListNode node) {
if (tail == null) {
head = node;
tail = head;
} else {
tail.next = node;
tail = node;
}
return new ListNode[]{head, tail};
}
}
首先,将链表分割为长度相等(或长度相差一)的两半。
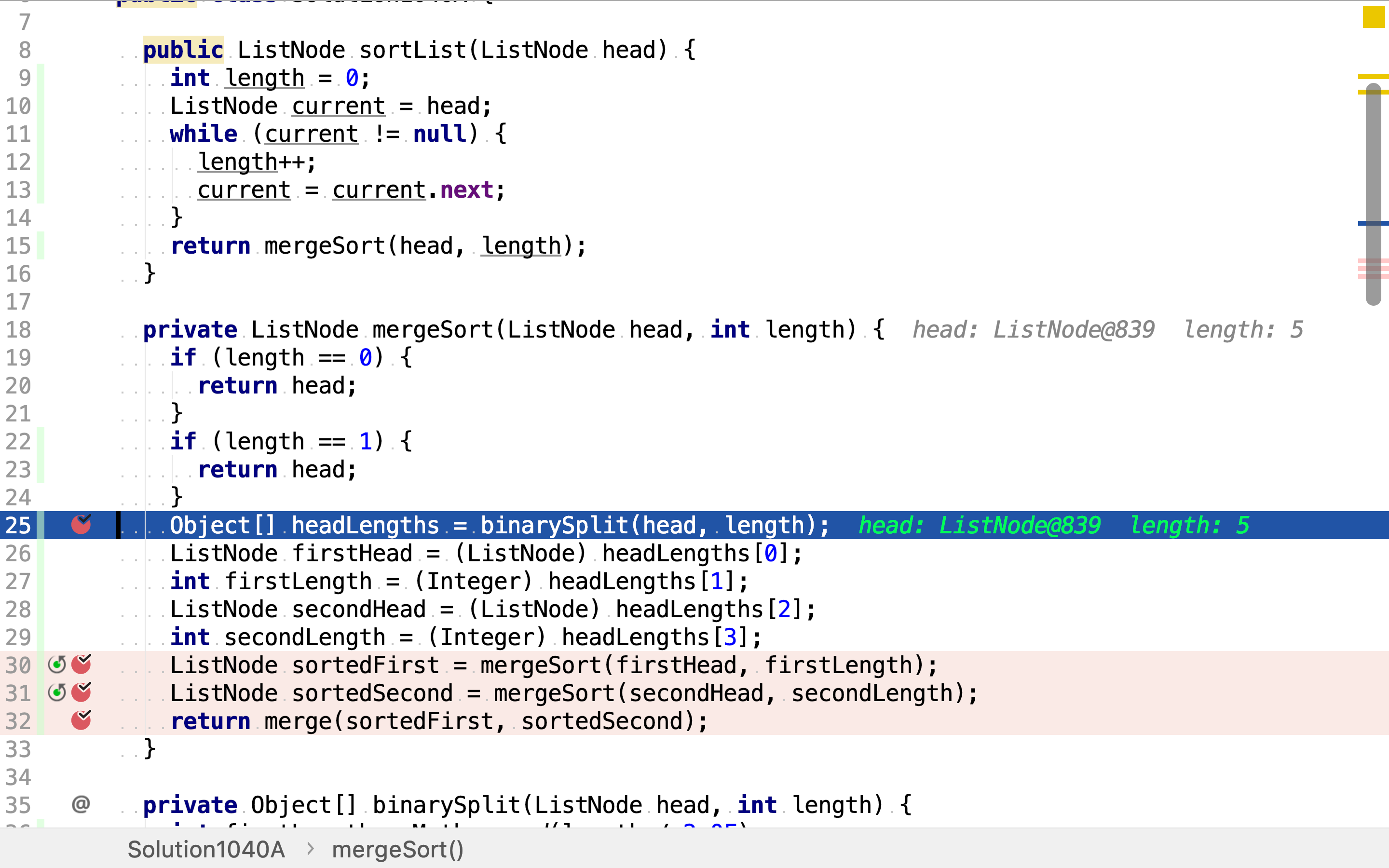
然后,递回排序两半链表。
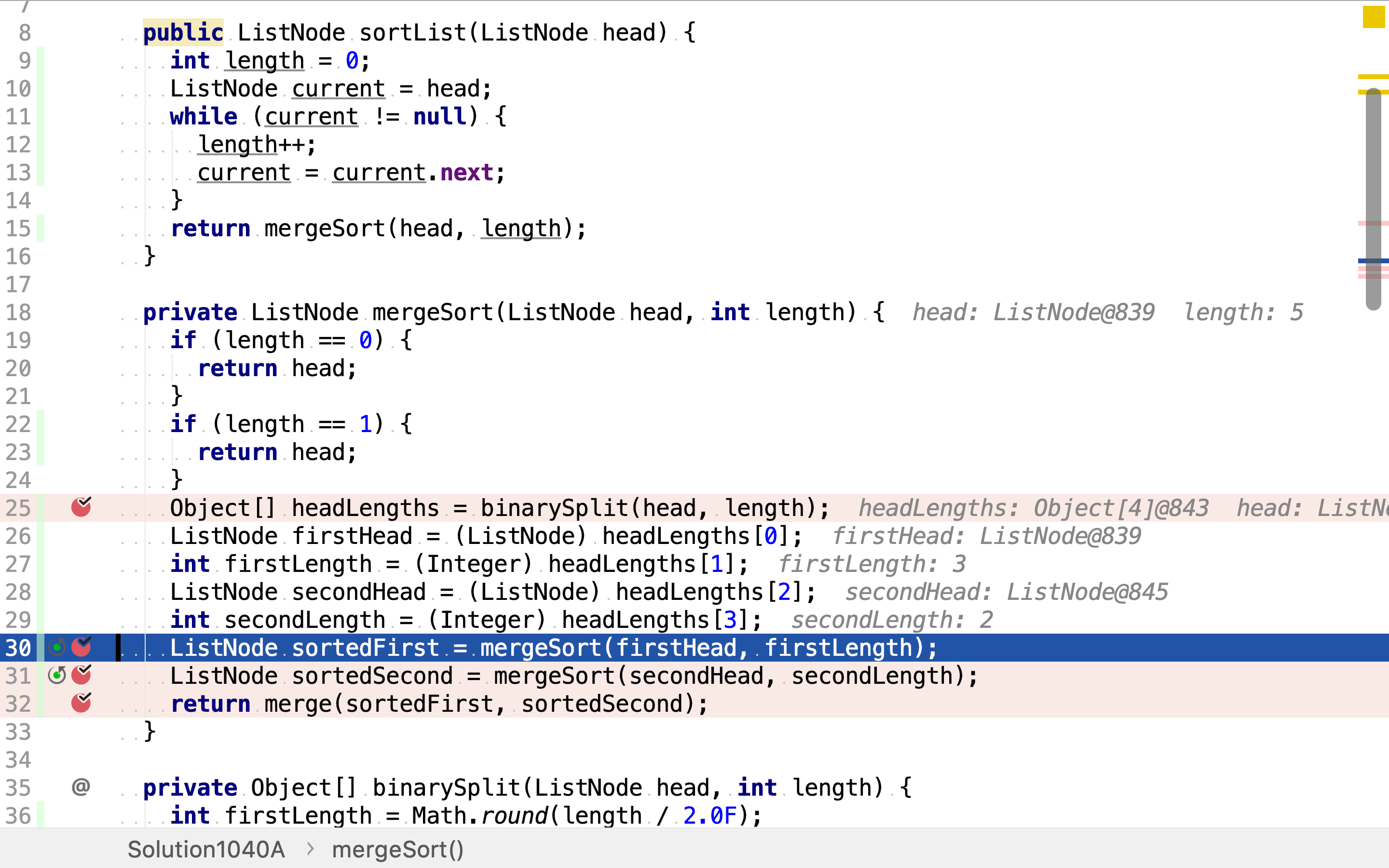
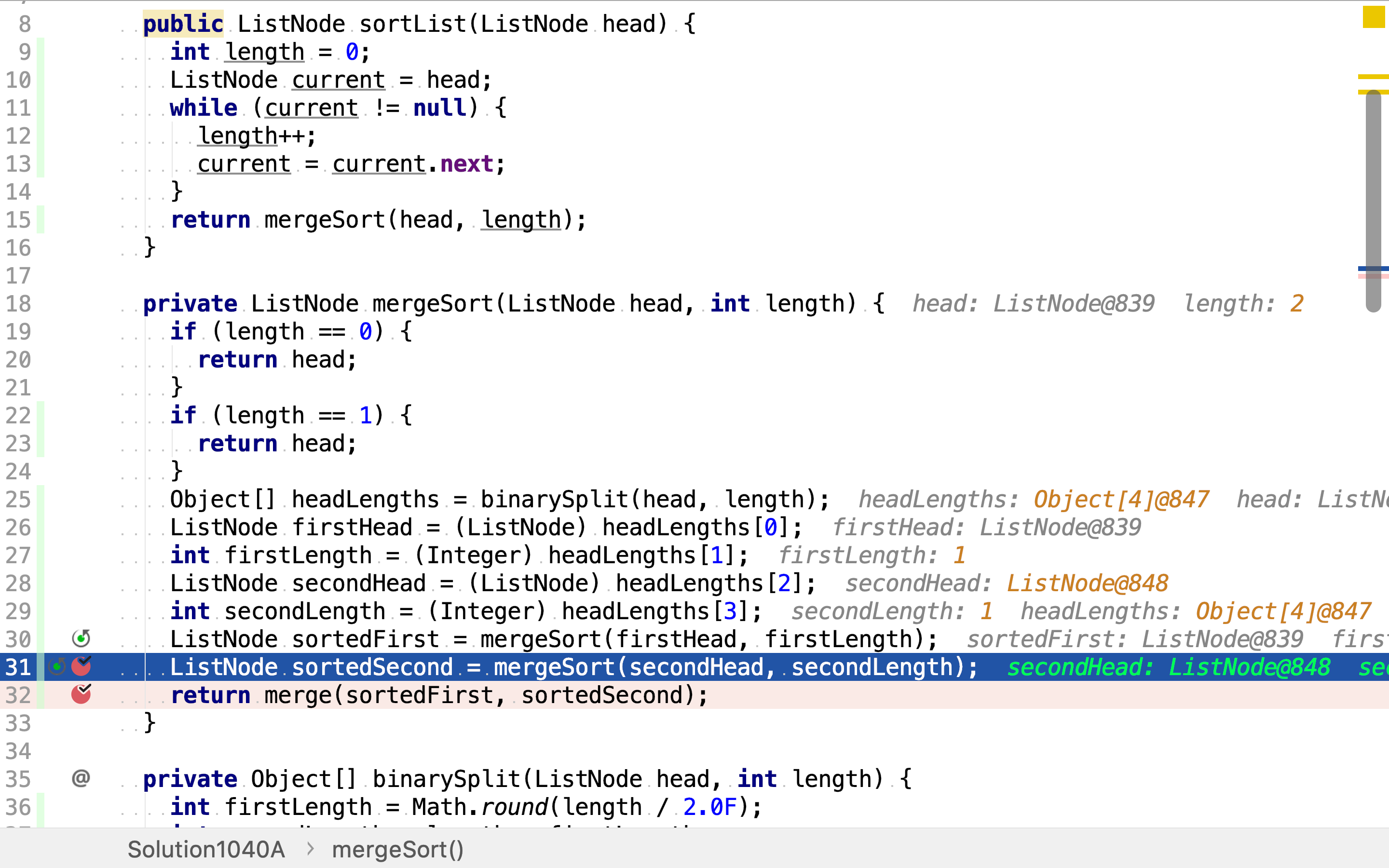
最后,将排好序的两半链表合併。
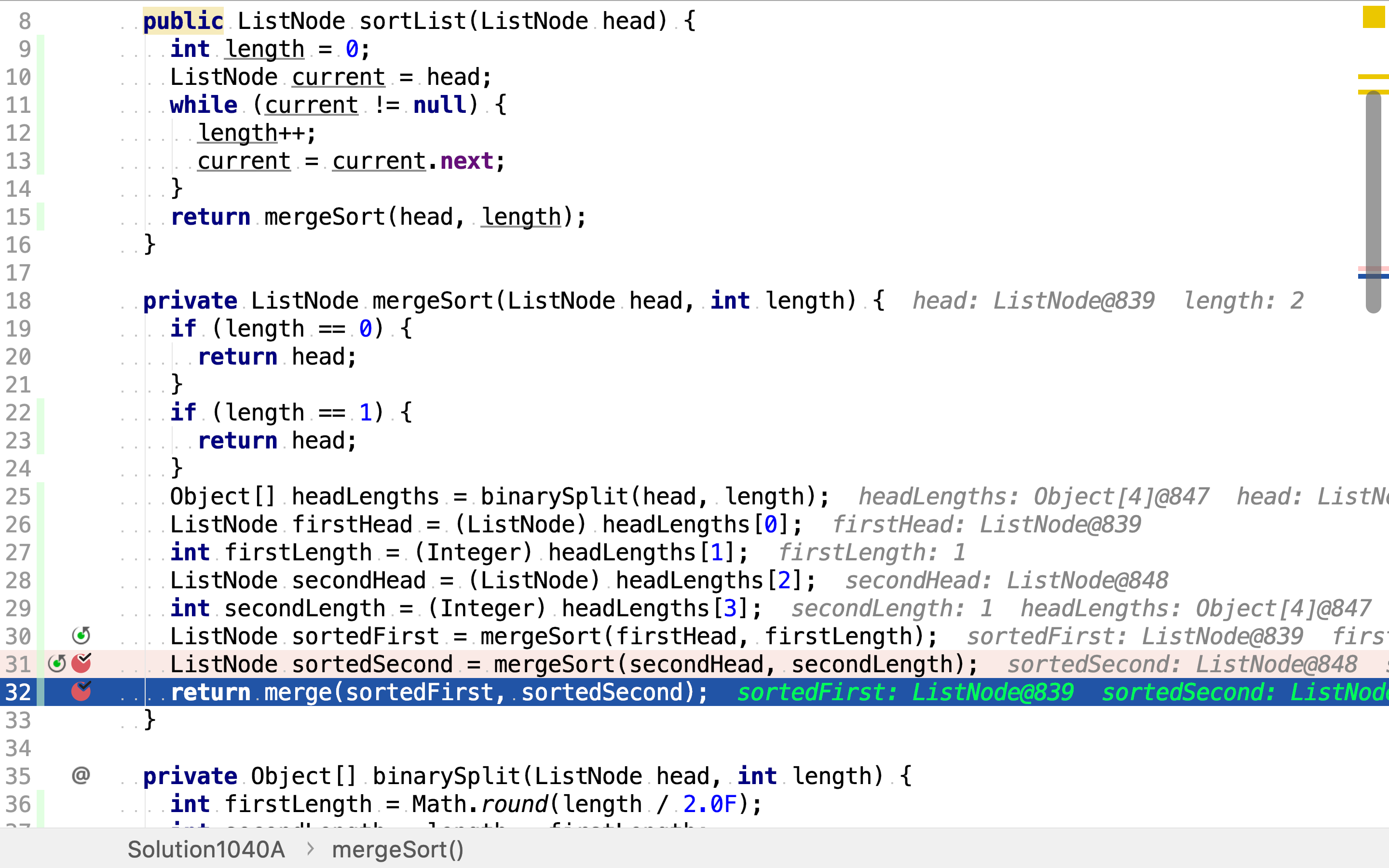
复杂度分析
时间复杂度
合併排序的时间复杂度为:
空间复杂度
所有的分割和合併操作都只是改变ListNode的next引用,并没有佔用新的空间。所以空间复杂度为:
快速排序
快速排序(英语:Quicksort),又称划分交换排序(partition-exchange sort),简称快排,一种排序演算法,最早由东尼·霍尔提出。在平均状况下,排序个项目要(大O符号)次比较。在最坏状况下则需要次比较,但这种状况并不常见。事实上,快速排序通常明显比其他演算法更快,因为它的内部回圈(inner loop)可以在大部分的架构上很有效率地达成。
演算法
快速排序使用分治法(Divide and conquer)策略来把一个序列(list)分为较小和较大的2个子序列,然后递回地排序两个子序列。
步骤为:
- 挑选基准值:从数列中挑出一个元素,称为「基准」(pivot),
- 分割:重新排序数列,所有比基准值小的元素摆放在基准前面,所有比基准值大的元素摆在基准后面(与基准值相等的数可以到任何一边)。在这个分割结束之后,对基准值的排序就已经完成,
- 递回排序子序列:递回地将小于基准值元素的子序列和大于基准值元素的子序列排序。
递回到最底部的判断条件是数列的大小是零或一,此时该数列显然已经有序。
选取基准值有数种具体方法,此选取方法对排序的时间效能有决定性影响。
举个例子,给定链表3->2->1->5->4。
- 首先,选取头元素
3为pivot,将所有其它元素分为比pivot小和比pivot大(或相等)的两个链表。
- 然后,再递回步骤1分割两个链表,直至链表长度为一或空。
- 最后,向上合併。
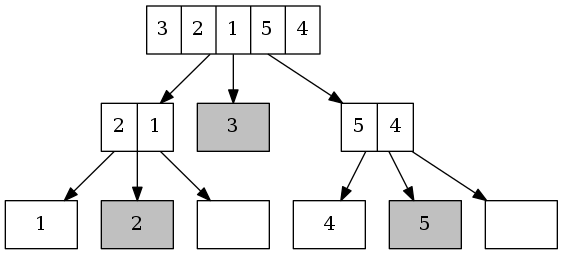
向上合併时,pivot左右链表已经是有序的了,且左边链表元素全小于pivot,右边链表元素都大于(或等于)pivot。所以合併时只需按左边链表、pivot、右边链表的顺序拼接即可。
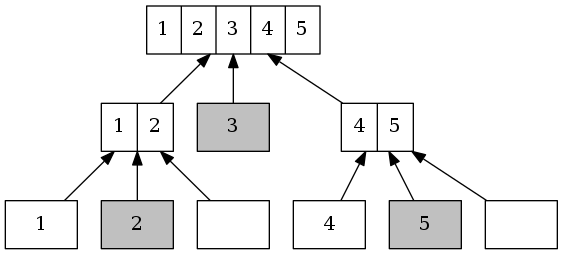
代码
package io.github.rscai.leetcode.bytedance.linktree;
/**
* Quick sort
*/
public class Solution1040B {
public ListNode sortList(ListNode head) {
return quickSort(head);
}
private ListNode quickSort(ListNode head) {
if (head == null) {
return head;
}
if (head.next == null) {
return head;
}
ListNode[] lists = divide(head);
ListNode first = lists[0];
ListNode pivot = lists[1];
ListNode second = lists[2];
ListNode sortedFirst = quickSort(first);
ListNode sortedSecond = quickSort(second);
ListNode sortedHead = sortedFirst;
ListNode sortedTail = sortedHead;
while (sortedTail != null && sortedTail.next != null) {
sortedTail = sortedTail.next;
}
if (sortedTail != null) {
sortedTail.next = pivot;
} else {
sortedHead = pivot;
sortedTail = pivot;
}
pivot.next = sortedSecond;
return sortedHead;
}
private ListNode[] divide(ListNode head) {
ListNode pivot = head;
ListNode firstHead = null;
ListNode firstTail = firstHead;
ListNode secondHead = null;
ListNode secondTail = secondHead;
ListNode current = head.next;
pivot.next = null;
while (current != null) {
ListNode next = current.next;
current.next = null;
if (current.val < pivot.val) {
if (firstTail == null) {
firstTail = current;
firstHead = firstTail;
} else {
firstTail.next = current;
firstTail = firstTail.next;
}
} else {
if (secondTail == null) {
secondTail = current;
secondHead = secondTail;
} else {
secondTail.next = current;
secondTail = secondTail.next;
}
}
current = next;
}
return new ListNode[]{firstHead, pivot, secondHead};
}
}
首先,将链表分割为pivot、小于pivot和大于(或等于)pivot三部份。
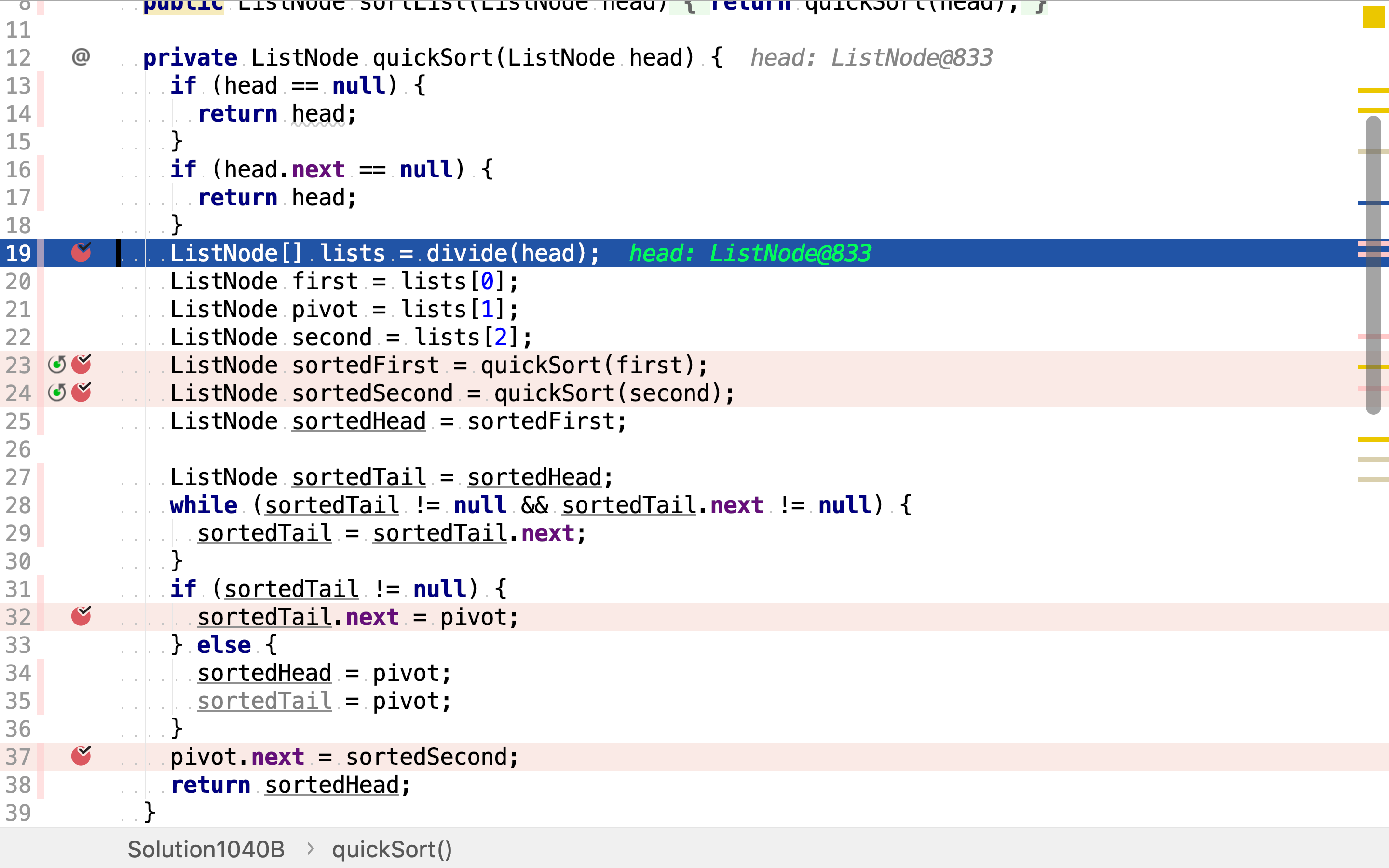
然后,递回排序小于pivot和大于pivot的链表。
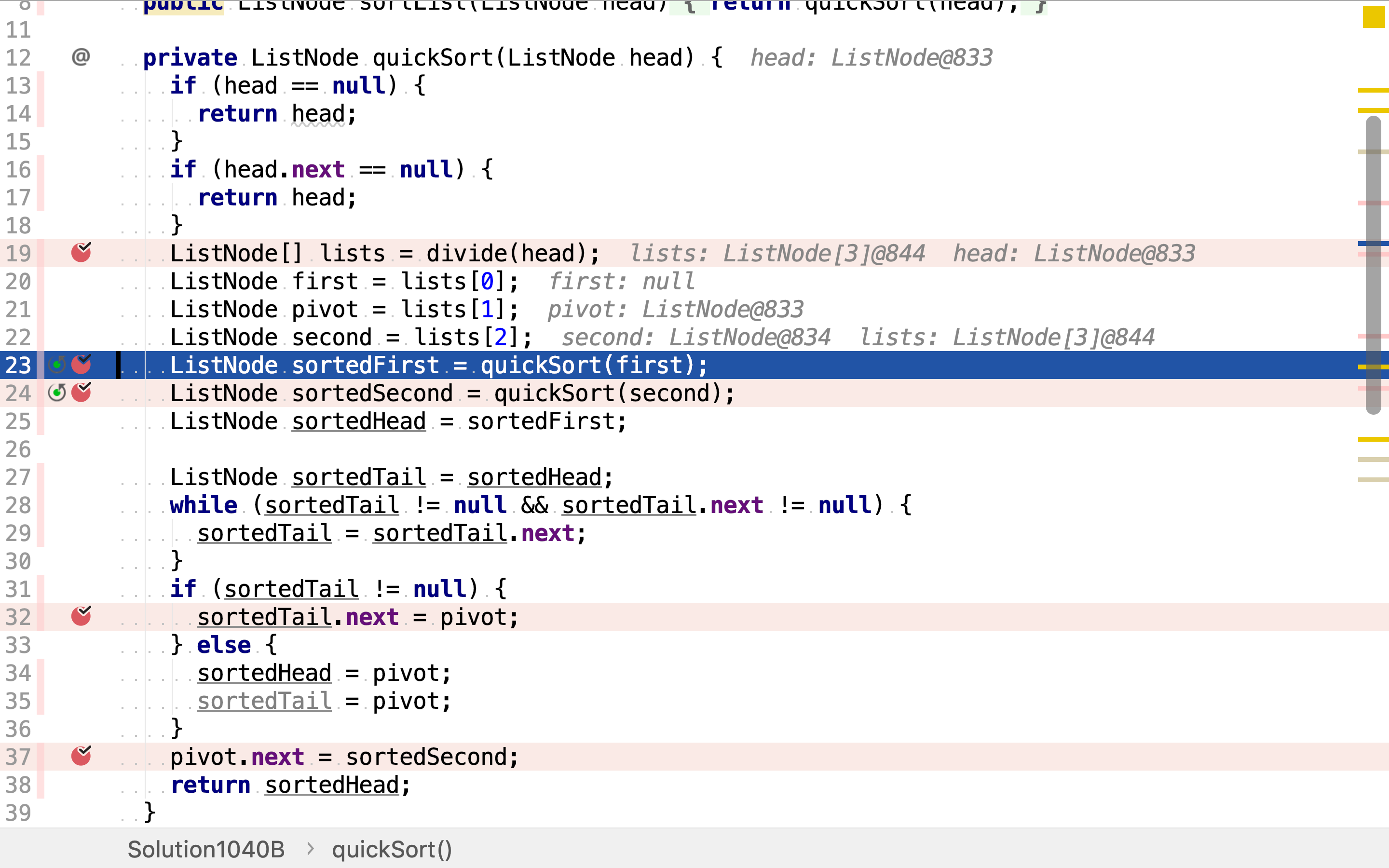
最后,将排序后的小于pivot链表、pivot和排序后的大于pivot链表按序拼接。
复杂度分析
时间复杂度
在最好的情况,每次我们执行一次分割,我们会把一个数列分为两个几近相等的片段。这个意思就是每次递回唿叫处理一半大小的数列。因此,在到达大小为一的数列前,我们只要作次巢状的唿叫。这个意思就是唿叫树的深度是。但是在同一阶层的两个程式唿叫中,不会处理到原来数列的相同部份;因此,程式唿叫的每一阶层总共全部仅需要的时间(每个唿叫有某些共同的额外耗费,但是因为在每一阶层仅仅只有个唿叫,这些被归纳在系数中)。结果是这个演算法仅需使用时间。
空间复杂度
链表的分割与合併都只是改变ListNode.next的引用,并没有佔用新的空间。所以空间复杂度为。
参考
















