数组中的第K个最大元素

题目

在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例 1:

输入: [3,2,1,5,6,4] 和 k = 2
输出: 5

示例 2:

输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4

说明:

你可以假设 k 总是有效的，且 1 ≤ k ≤ 数组的长度。

快速排序法

先使用JDK提供的快速排序算法排序数组，再取倒数第k个值。

快速排序

快速排序（英语：Quicksort），又称划分交换排序（partition-exchange sort），简称快排，一种排序演算法，最早由东尼·霍尔提出。在平均状况下，排序$n$个项目要${\displaystyle \ O(n\log n)}$（大O符号）次比较。在最坏状况下则需要${\displaystyle O(n^{2})}$次比较，但这种状况并不常见。事实上，快速排序${\displaystyle \Theta (n\log n)}$通常明显比其他演算法更快，因为它的内部回圈（inner loop）可以在大部分的架构上很有效率地达成。

演算法

快速排序使用分治法（Divide and conquer）策略来把一个序列（list）分为较小和较大的2个子序列，然后递回地排序两个子序列。

步骤为：

1. 挑选基准值：从数列中挑出一个元素，称为「基准」（pivot），
2. 分割：重新排序数列，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准后面（与基准值相等的数可以到任何一边）。在这个分割结束之后，对基准值的排序就已经完成，
3. 递回排序子序列：递回地将小于基准值元素的子序列和大于基准值元素的子序列排序。

递回到最底部的判断条件是数列的大小是零或一，此时该数列显然已经有序。

代码

    /*
     * Sorting methods. Note that all public "sort" methods take the
     * same form: Performing argument checks if necessary, and then
     * expanding arguments into those required for the internal
     * implementation methods residing in other package-private
     * classes (except for legacyMergeSort, included in this class).
     */

    /**
     * Sorts the specified array into ascending numerical order.
     *
     * <p>Implementation note: The sorting algorithm is a Dual-Pivot Quicksort
     * by Vladimir Yaroslavskiy, Jon Bentley, and Joshua Bloch. This algorithm
     * offers O(n log(n)) performance on many data sets that cause other
     * quicksorts to degrade to quadratic performance, and is typically
     * faster than traditional (one-pivot) Quicksort implementations.
     *
     * @param a the array to be sorted
     */
    public static void sort(int[] a) {
        DualPivotQuicksort.sort(a, 0, a.length - 1, null, 0, 0);
    }

复杂度分析

时间复杂度

Arrays.sort实现的是「Dual-Pivot」快速排序。时间复杂度是$\mathcal{O}(n \log{n})$。

二分定位法

快速排序使用「基准（pivot）」将数组分为大小两个子数组，再递归排序两个子数组。当大小两个数组划分完成时，基准所处的位置即其在有序数组中最终所处的位置。所有小数子数组中的元素其最终位置都小于基准，所有大数子数组中的元素其最终位置都大于基准。所以，在确定基准元素所处位置后，就可以确定所求第k个元素处于大小两个子数组中的某一个。

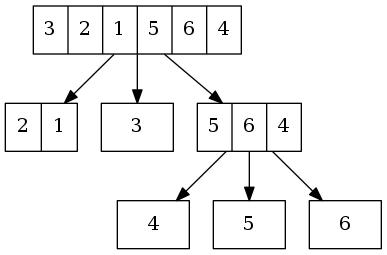
举个例子，给定数组[3,2,1,5,6,4]，求第2大的值。

首先，以3为基准，将小于3的值都移到左侧﹐大于等于3的值都移到右侧，得到数组[2,1,3,5,6,4]。基准3位置2(0-based)，其是第4大元素，第2大的元素在右侧大于3的子数组中。

然后，在右侧子数组[5,6,4]中，以5为基准，将小于5的元素都移至其左侧，大于等于5的元素移至右侧，得到数组[4,5,6]。基准5位置1，正是所求第2大的元素。

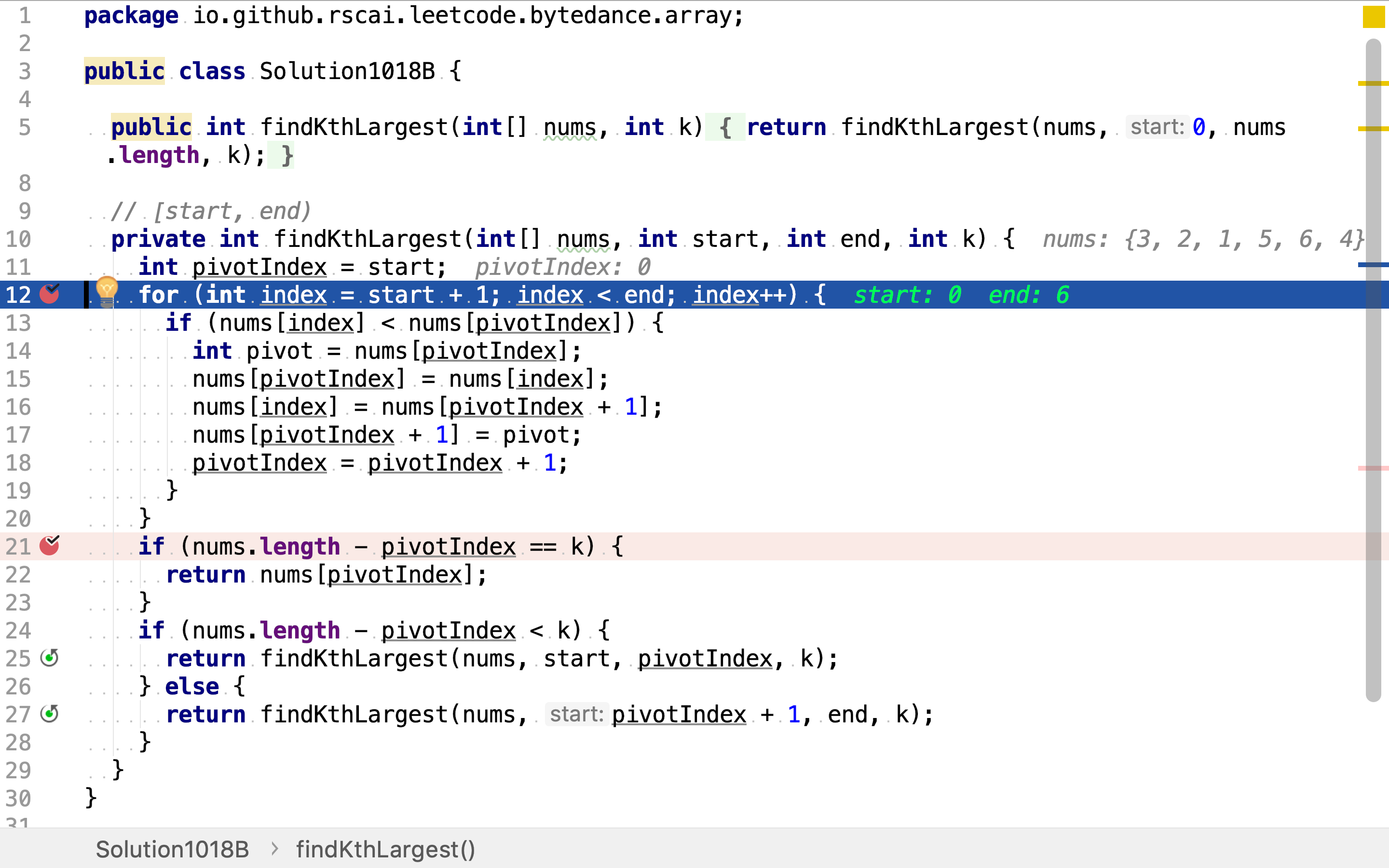
代码

先使用「快速排序」中使用的基准法，将数组分为小于和大于基准的两部份。

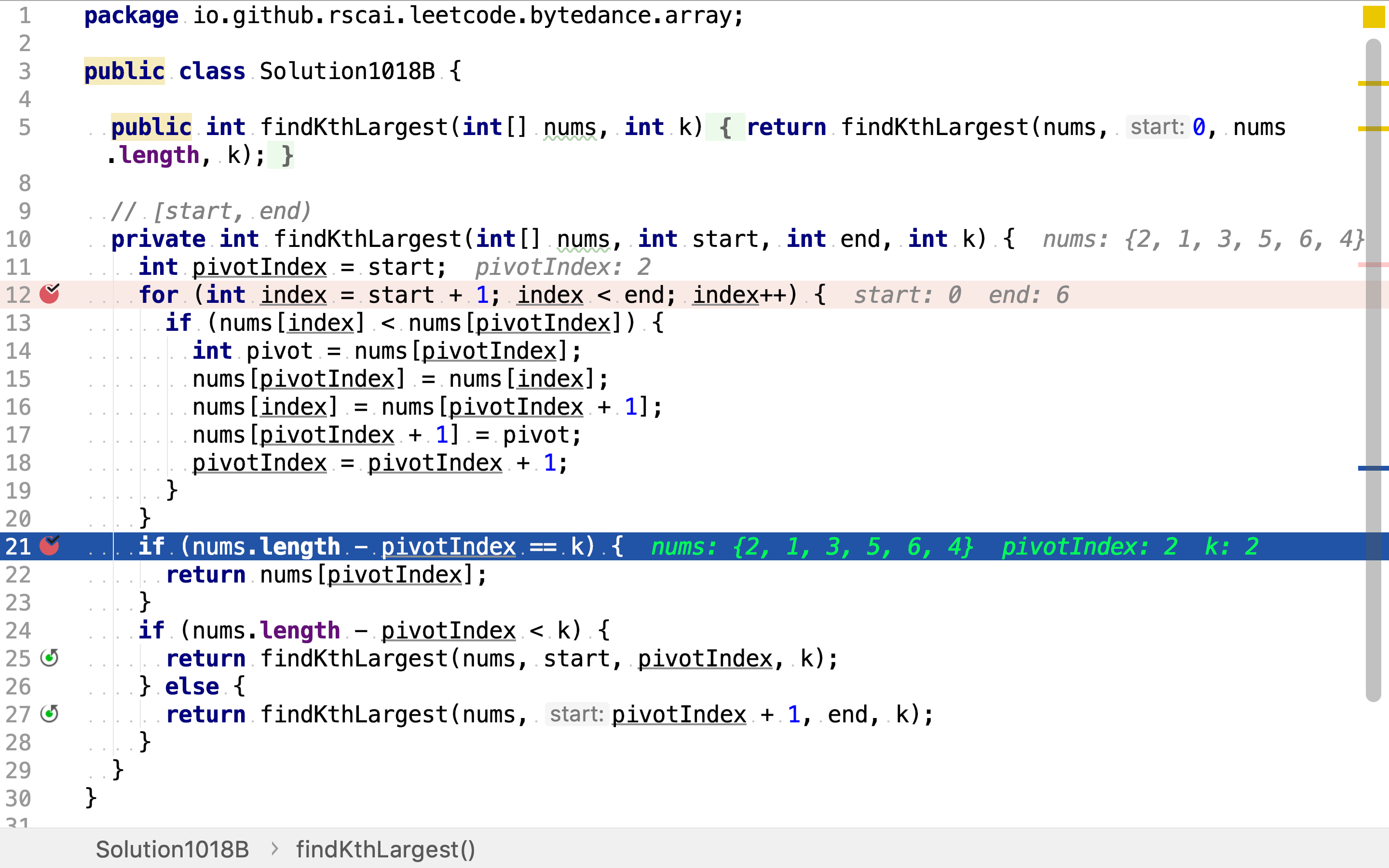
然后，判断基准是否就是所求第k大值。若是则计算结束；若第k大值在小于基准的子数组中，则在其中递归寻找第k大值；若第k大值在大于基准的子数组中，则在其中递归寻找第k大值。

复杂度分析

时间复杂度

一般情况下，每一次基准都把数组分成相等的两部份。设初始数组长度$n$，则每一次划分后的一个数组长度为$\frac{n}{2^0}, \frac{n}{2^1}, \frac{n}{2^2}, ..., 1$。时间复杂度为所有数组长度的累和：

$$\begin{aligned} C_{time} &= \frac{n}{2^0} + \frac{n}{2^1} + \frac{n}{2^2} + ... + 1 \\ &= \frac{2 \times (\frac{n}{2^0} + \frac{n}{2^1} + \frac{n}{2^2} + ... + 1) - 1 \times (\frac{n}{2^0} + \frac{n}{2^1} + \frac{n}{2^2} + ... + 1)}{2 - 1} \\ &= (2n + \frac{n}{2^0} + \frac{n}{2^1} + ... + 2) - (\frac{n}{2^0} + \frac{n}{2^1} + \frac{n}{2^2} + ... + 1) \\ &= 2n +1 \\ &= \mathcal{O}(n) \end{aligned}$$

空间复杂度

使用四个变量start, end, pivotIndex, pivot。空间复杂度为$\mathcal{O}(1)$。

参考

• 快速排序