简化路径

题目

以 Unix 风格给出一个文件的绝对路径，你需要简化它。或者换句话说，将其转换为规范路径。

在Unix 风格的文件系统中，一个点（.）表示当前目录本身；此外，两个点（..） 表示将目录切换到上一级（指向父目录）；两者都可以是复杂相对路径的组成部分。更多信息请参阅：Linux / Unix中的绝对路径 vs 相对路径

请注意，返回的规范路径必须始终以斜杠 / 开头，并且两个目录名之间必须只有一个斜杠 /。最后一个目录名（如果存在）不能以 / 结尾。此外，规范路径必须是表示绝对路径的最短字符串。

示例 1：

输入："/home/"
输出："/home"
解释：注意，最后一个目录名后面没有斜杠。

示例 2：

输入："/../"
输出："/"
解释：从根目录向上一级是不可行的，因为根是你可以到达的最高级。

示例 3：

输入："/home//foo/"
输出："/home/foo"
解释：在规范路径中，多个连续斜杠需要用一个斜杠替换。

示例 4：

输入："/a/./b/../../c/"
输出："/c"

示例 5：

输入："/a/../../b/../c//.//"
输出："/c"

示例 6：

输入："/a//b////c/d//././/.."
输出："/a/b/c"

确定有限状态机法

使用「确定有限状态机」将路径中的各级节点解析出来，再重新构造简化的路径。

确定有限状态自动机

在计算理论中，确定有限状态自动机或确定有限自动机（英语：deterministic finite automaton, DFA）是一个能实现状态转移的自动机。对于一个给定的属于该自动机的状态和一个属于该自动机字母表 $\Sigma$ 的字元，它都能根据事先给定的转移函式转移到下一个状态（这个状态可以是先前那个状态）。

基础概念

定义

确定有限状态自动机 ${\mathcal {A}}$ 是由

• 一个非空有限的状态集合 $Q$
• 一个输入字母表 $\Sigma$ （非空有限的字元集合）
• 一个转移函式 $\delta :Q\times \Sigma \rightarrow Q$（例如： $\delta \left(q,\sigma \right)=p,\left(p,q\in Q,\sigma \in \Sigma \right)$）
• 一个开始状态 $s\in Q$
• 一个接受状态的集合 $F\subseteq Q$

所组成的5-元组。因此一个DFA可以写成这样的形式： ${\mathcal {A}}=\left(Q,\Sigma ,\delta ,s,F\right)$。

工作方式（非正式的语意)

确定有限状态自动机从起始状态开始，一个字元接一个字元地读入一个字串 $w\in \Sigma ^{*}$（这里的 ${}^{*}$指示Kleene星号算子。），并根据给定的转移函式一步一步地转移至下一个状态。在读完该字串后，如果该自动机停在一个属于F的接受状态，那么它就接受该字串，反之则拒绝该字串。

扩充转移函式

为了在保证严谨的前提下，方便地叙述关于DFA的内容，我们定义如下扩充的转移函式：$\delta ^{*}:Q\times \Sigma ^{*}\rightarrow Q$。

• 其中$\delta ^{*}\left(q,w\right)$是自动机从状态q顺序读入字串w后达到的状态
• 扩充转移函式递回的定义为：
  • $\delta ^{*}\left(q,\epsilon \right)=q$
  • $\delta ^{*}\left(q,u\sigma \right)=\delta (\delta ^{*}(q,u),\sigma ),\forall u\in \Sigma ^{*},\sigma \in \Sigma$

工作方式（正式的语意）

对于一个确定有限状态自动机 ${\mathcal {A}}=\left(Q,\Sigma ,\delta ,s,F\right)$，如果 $\delta ^{*}\left(s,w\right)\in F$，我们就说该自动机接受字串w，反之则表明该自动机拒绝字串w。

被一个确定有限自动机接受的语言（或者叫「被辨识的语言」）定义为： ${\mathcal {L}}({\mathcal {A}})=\{w\in \Sigma ^{*}|{\mathcal {A}}~接受字串 ~w\}，$也就是由所有被接受的字串组成的集合。

参考

• 确定有限状态自动机

定义,

• 非空有限状态集合{start, waitForMoreNodeChar, receivedDot, receivedTwoDot}
• 输入字母表{'/','.',其它}
• 转移函数

• 开始状态start
• 接受状态集合{start}

代码实现

先将路径中的节点都解柝出来，再重新构造简化的路径。

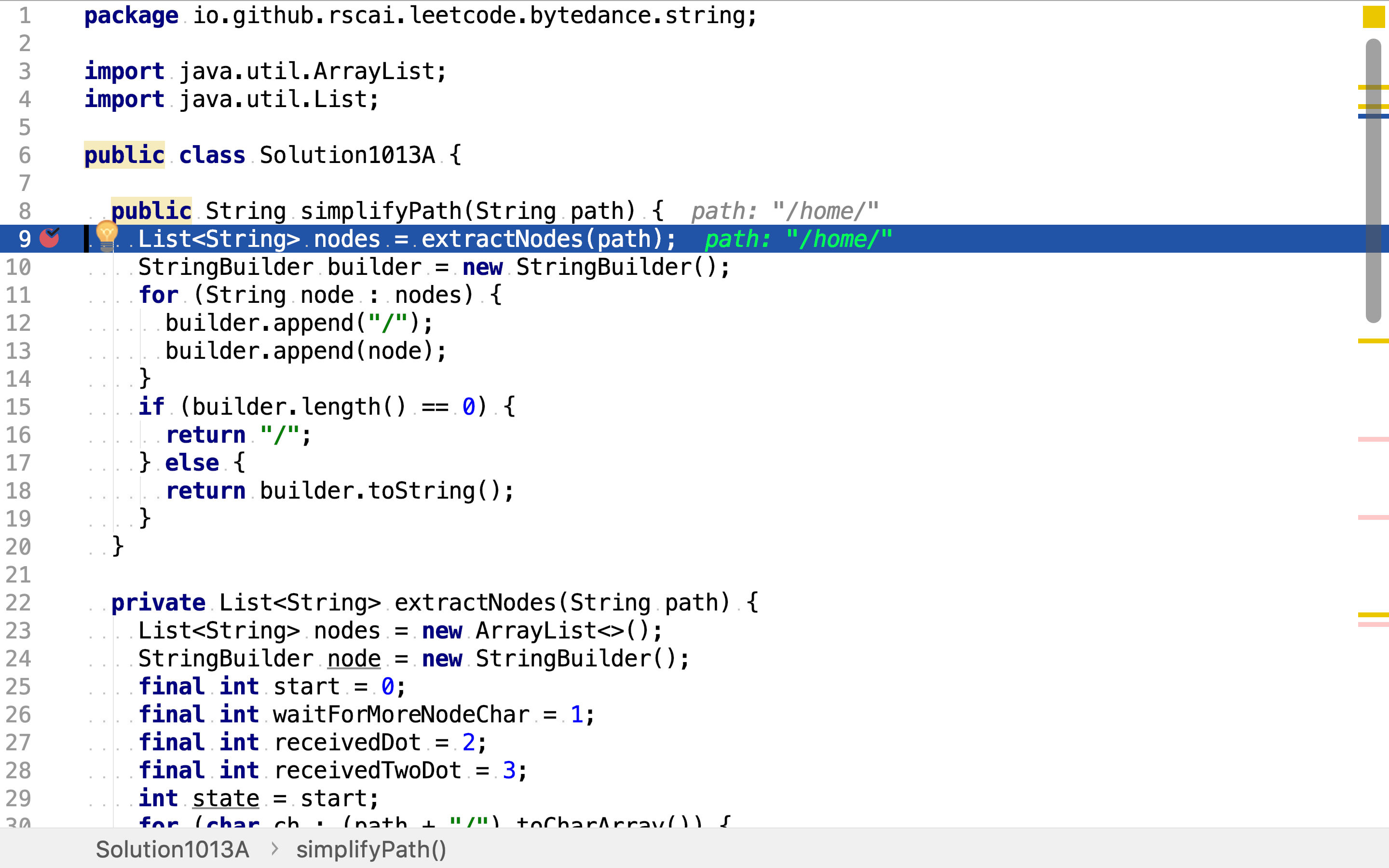
路径解柝使用确定有限状态机实现。其初始状态为start，当：

• 遇到'/'时，无动作，无状态转移
• 遇到'.'时，转移至状态receivedDot
• 遇到其它字符时，将字符存入node缓存，并转移状态至waitForMoreNodeChar

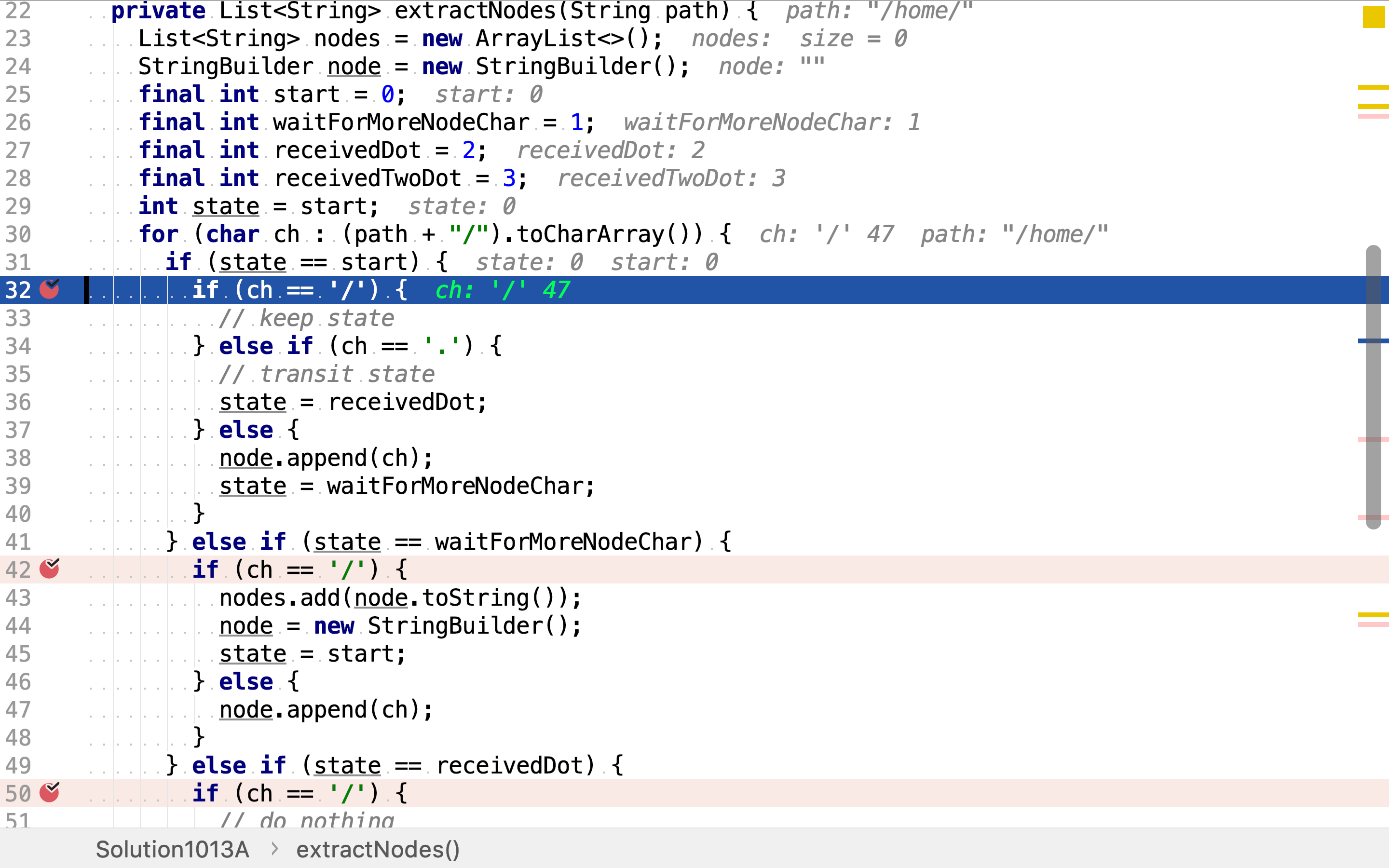
处于状态waitForMoreNodeChar，当：

• 遇到'/'时，轮出node中的缓存的字符为一个新的node，并转移状态至start
• 遇到其它字符时，则将其存入node

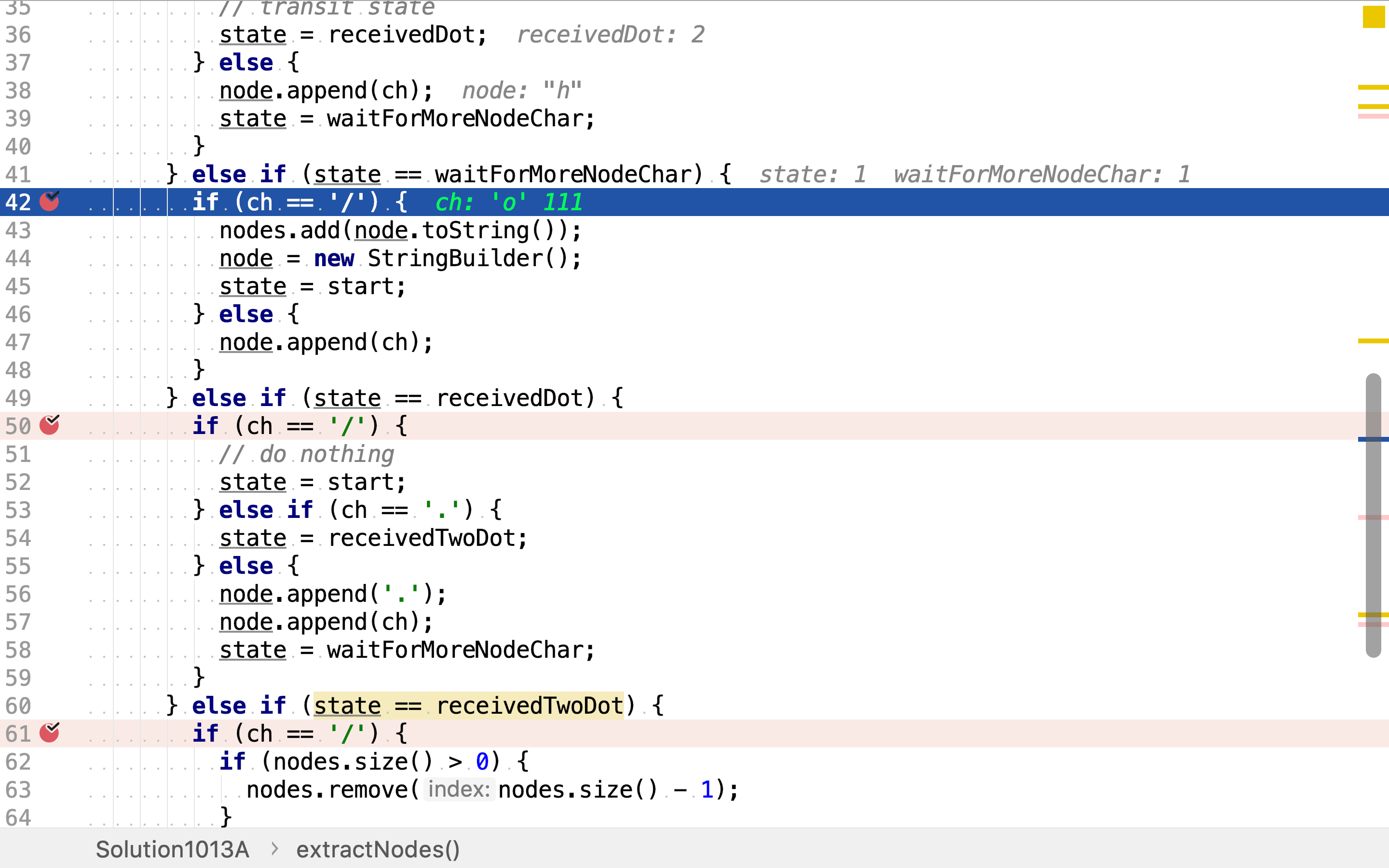
处于状态receivedDot，当：

• 遇到'/'时，转移状态至start
• 遇到'.'时，转移状态至qreceivedTwoDot`
• 遇到其它字符，则将之前收到的'.'及当前收到的字符存入node，并转移状态至waitForMoreNodeChar

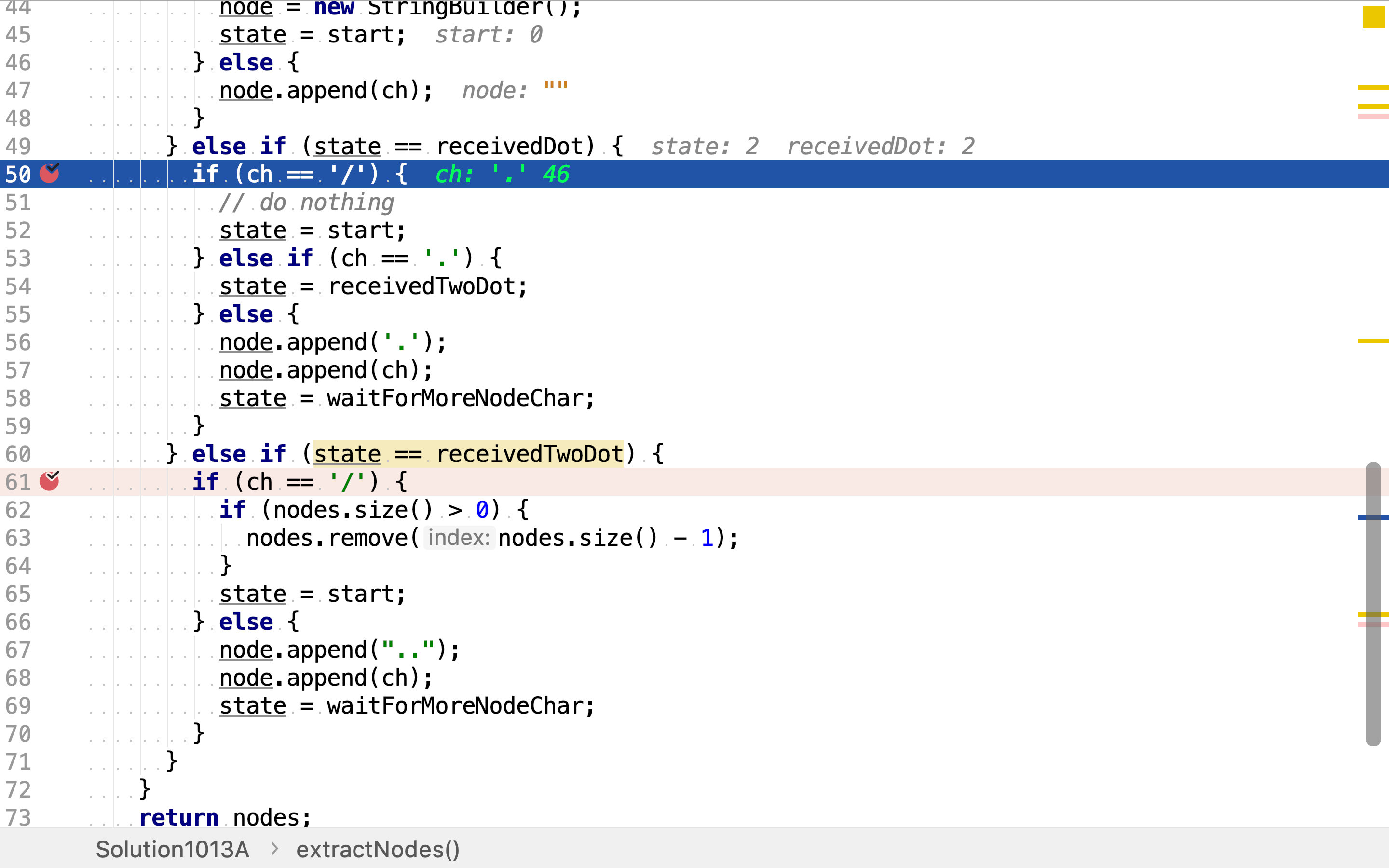
处于状态receivedTwoDot，当：

• 遇到'/'，则移除最后一个已解柝出的节点
• 遇到其它字符，则将之前收到的两个'.'及当前收到字符一併加入node，并转移状态至waitForMoreNodeChar

debug-A5

复杂度分析

时间复杂度

extractNodes只遍历了一遍path，时间复杂度为$\mathcal{O}(n)$。

空间复杂度

使用了变量nodes, builder，其最大佔空间都为n。所以空间复杂度为$\mathcal{O}(n)$。