朋友圈

题目

班上有N名学生。其中有些人是朋友，有些则不是。他们的友谊具有是传递性。如果已知A是B的朋友，B是C的朋友，那么我们可以认为A也是C的朋友。所谓的朋友圈，是指所有朋友的集合。

给定一个N * N的矩阵M，表示班级中学生之间的朋友关系。如果M[i][j] = 1，表示已知第i个和j个学生互为朋友关系，否则为不知道。你必须输出所有学生中的已知的朋友圈总数。

示例 1：
输入:
[[1,1,0],
[1,1,0],
[0,0,1]]
输出: 2
说明：已知学生0和学生1互为朋友，他们在一个朋友圈。
第2个学生自己在一个朋友圈。所以返回2。
示例 2：
输入:
[[1,1,0],
[1,1,1],
[0,1,1]]
输出: 1
说明：已知学生0和学生1互为朋友，学生1和学生2互为朋友，所以学生0和学生2也是朋友，所以他们三个在一个朋友圈，返回1。
注意：

N 在[1,200]的范围内。

对于所有学生，有M[i][i] = 1。

如果有M[i][j] = 1，则有M[j][i] = 1。

深度优先搜寻图连通分量法

此题可以抽象为求图的连通分量。

连通分量

在图论中，元件又称为连通元件、分量、或分支，是一个无向子图，在元件中的任何两个顶点都可以经由该图上的边抵达另一个顶点，且没有任何一边可以连到其他子图的顶点。

演算法

一种直接了当的以线性时间（以图的顶点和边数量计）计算图连通分量的方法是使用广度优先搜寻或深度优先搜寻。在任何一种情况下，从某个顶点v开始的搜索将会返回包含v的完整连通分量。要找到图的所有连通分量，只需遍历每一个顶点，以每一个顶点为起点开始广度优先或深度优先搜寻。Hopcroft和Tarjan（1973）基本上描述了这种算法，并指出在那时它是“众所周知的”。

此题中，每一个朋友圈即一个连通分量。求朋友圈数量即求连通分量数量。

最直接求图连通分量的方法就使用「广度优先搜寻」和「深度优先搜寻」。依次以图中每一个点为起点，用「广度优先搜寻」或「深度优先搜寻」搜寻以起点为根节点的树，该树即为一个图的连通分量。将所有搜寻到的树去重后得到的集合即为该图的所有连通分量。

举个例子，假设有如下图：

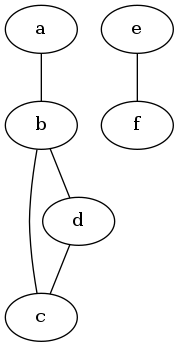
以a为起点，深度优先搜寻，找到连通分量a, b, c, d，并记录已访问的点。

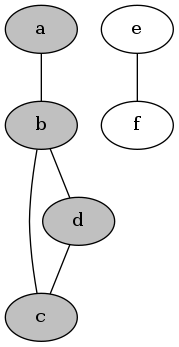
再以b, c, d为起点，但它们都已经被访问过了。

再以e为起点，深度优先搜寻，找到连通分量e, f，并记录已访问的点。

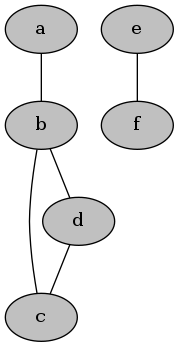
再以f为起点，发现其已经被访问过了。至此，遍历完所有点了。得到了图的全部连通分量a, b, c, d和e, f。

代码实现

package io.github.rscai.leetcode.bytedance.array; import java.util.HashSet; import java.util.Set; public class Solution1036B { public int findCircleNum(int[][] M) { int count = 0; for (int start = 0; start < M.length; start++) { Set<Integer> component = depthFirstSearch(M, start, new HashSet<>()); if (component.size() > 0) { count++; } } return count; } private Set<Integer> depthFirstSearch(int[][] graph, int start, Set<Integer> accessed) { if (graph[start][start] == 0) { return accessed; } accessed.add(start); graph[start][start] = 0; int child = nextChild(graph, start, accessed); while (child > -1) { accessed = depthFirstSearch(graph, child, accessed); graph[start][child] = 0; graph[child][start] = 0; child = nextChild(graph, start, accessed); } return accessed; } private int nextChild(int[][] graph, int parent, Set<Integer> accessed) { for (int another = 0; another < graph.length; another++) { if (graph[parent][another] == 1 && !accessed.contains(another)) { return another; } } return -1; } }

首先，依旧是依次以每个点为起点，深度优先搜寻连通分量。

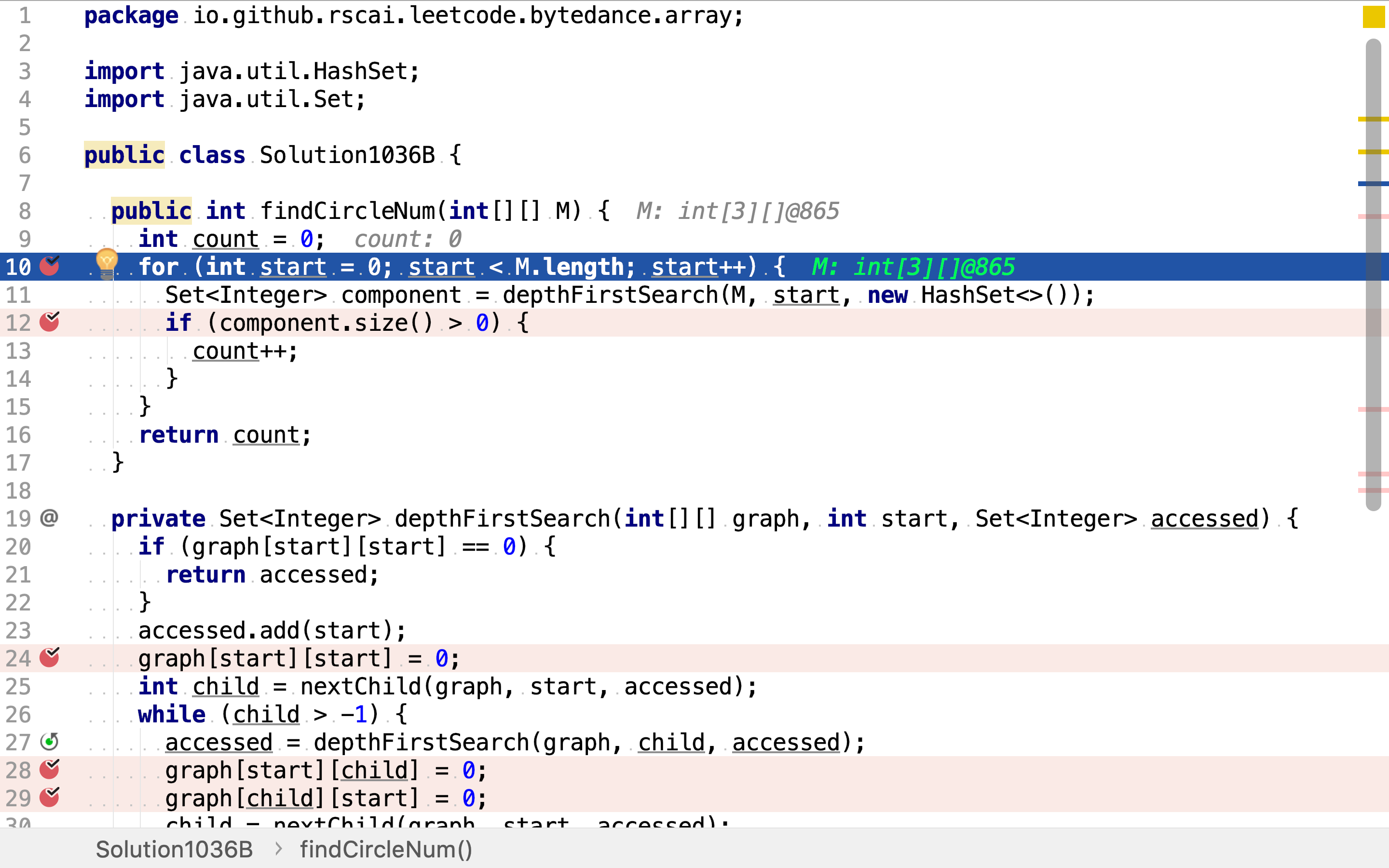
但深度优先搜寻时，将访问过的点和边都标记为已访问。

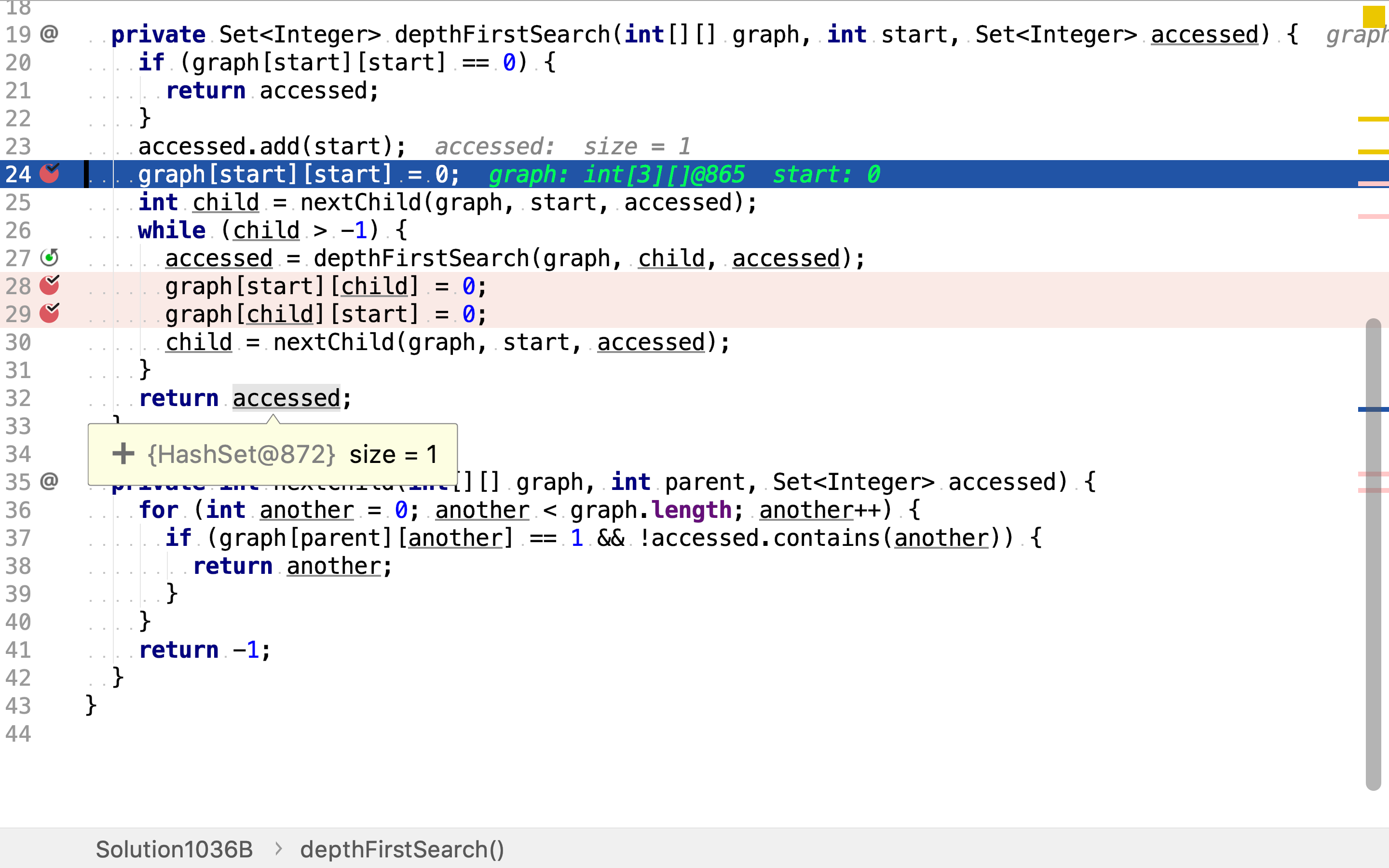
最后，直接累计搜寻到的连通分量即可。因为所有的点和边都祇被访问一次，所以不价出现重复的连通分量（包含的点相同）。

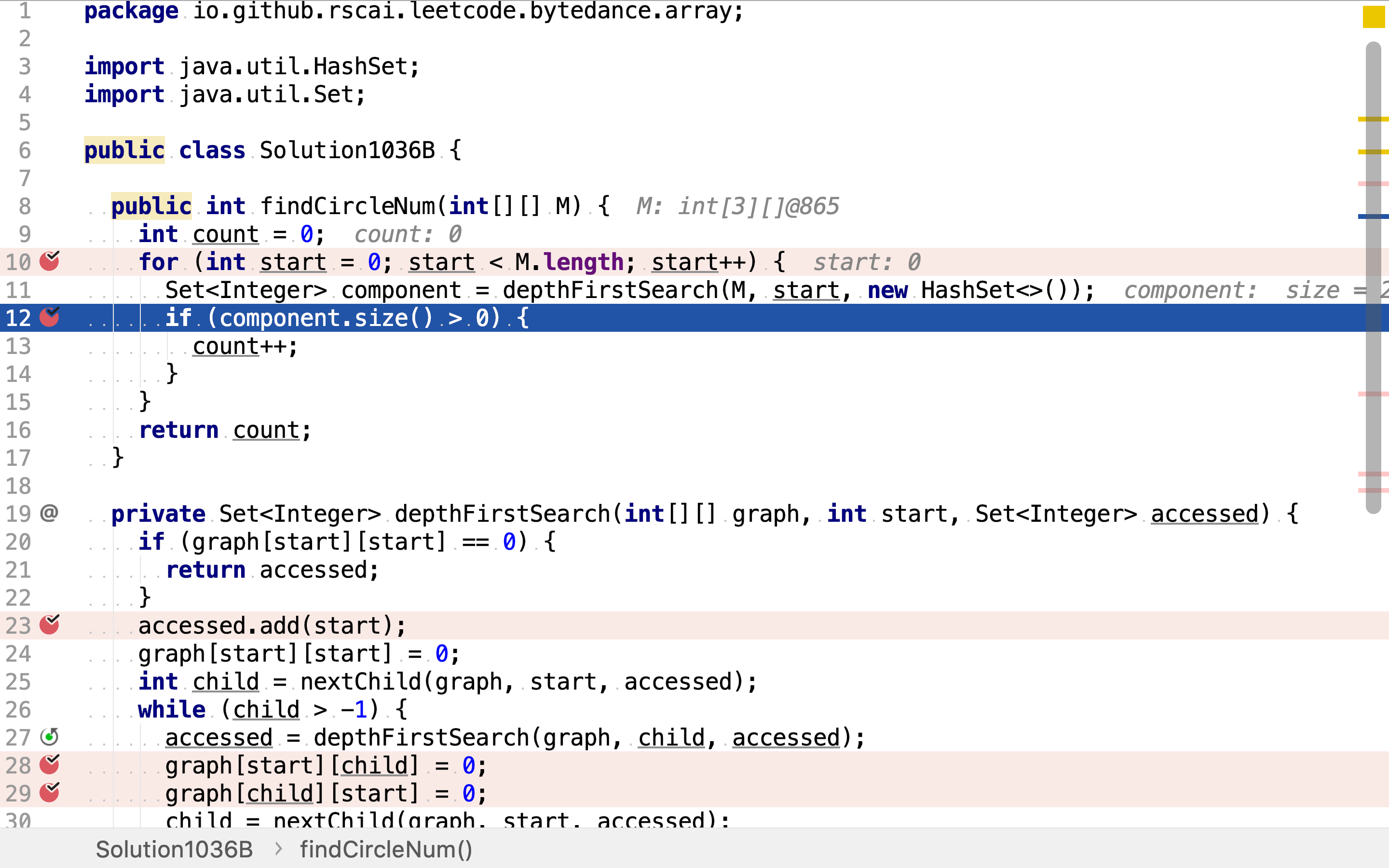
复杂度分析

时间复杂度

depthFirstSearch将访问过的点和边立即移除，所以虽然依旧依次以每个点为起点搜寻连通分量，但实际上每个点最多被访问两次，每条边被访问一次。时间复杂度为 $\mathcal{O}(n)$ 。

空间复杂度

depthFristSearch返回值最多包含 $n$ 个元素。空间复杂度为 $\mathcal{O}(n)$ 。

朋友圈

朋友圈

题目