字符串相乘
题目
给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。
示例 1:
输入: num1 = "2", num2 = "3" 输出: "6"示例 2:
输入: num1 = "123", num2 = "456" 输出: "56088"说明:
- num1 和 num2 的长度小于110。
- num1 和 num2 只包含数字 0-9。
- num1 和 num2 均不以零开头,除非是数字 0 本身。
- 不能使用任何标准库的大数类型(比如 BigInteger)或直接将输入转换为整数来处理。
乘法分配律
乘法分配律,也叫做乘法分配性质、十字相乘法或十字交乘法,公式是: 。
基本验证
和平方可直接利用因式分解验证。公式如下:
代码实现
package io.github.rscai.leetcode.bytedance.string;
public class Solution1015A {
private static final int OFFSET = 0x30;
public String multiply(String num1, String num2) {
char[] left = new StringBuilder(num1).reverse().toString().toCharArray();
int[] leftInts = new int[left.length];
for (int i = 0; i < left.length; i++) {
leftInts[i] = left[i] - OFFSET;
}
char[] right = new StringBuilder(num2).reverse().toString().toCharArray();
int[] rightInts = new int[right.length];
for (int i = 0; i < right.length; i++) {
rightInts[i] = right[i] - OFFSET;
}
int[] resultInts = new int[leftInts.length + rightInts.length];
for (int i = 0; i < rightInts.length; i++) {
int[] oneMultiplyResult = oneMultiply(leftInts, rightInts[i]);
resultInts = add(resultInts, oneMultiplyResult, i);
}
char[] result = new char[resultInts.length];
for (int i = 0; i < resultInts.length; i++) {
result[i] = (char) (resultInts[i] + OFFSET);
}
int endPos = result.length - 1;
while (endPos > 0 && result[endPos] == '0') {
endPos--;
}
return new StringBuffer(String.valueOf(result, 0, endPos + 1)).reverse().toString();
}
private int[] oneMultiply(int[] left, int right) {
int[] result = new int[left.length + 1];
int carry = 0;
for (int i = 0; i < left.length; i++) {
int value = left[i] * right + carry;
result[i] = value % 10;
carry = value / 10;
}
if (carry > 0) {
result[result.length - 1] = carry;
}
return result;
}
private int[] add(int[] left, int[] right, int offset) {
int carry = 0;
for (int i = 0; i < right.length; i++) {
int value = left[i + offset] + right[i] + carry;
left[i + offset] = value % 10;
carry = value / 10;
}
int index = right.length + offset;
while (carry > 0) {
left[index] = (left[index] + carry) % 10;
carry = (left[index] + carry) / 10;
index++;
}
return left;
}
}
先将字串表示的整数转化为整型数组并反序存储。乘法和加法都要考虑进位,从低位往高位处理会便于进位操作,所以将反序存储。
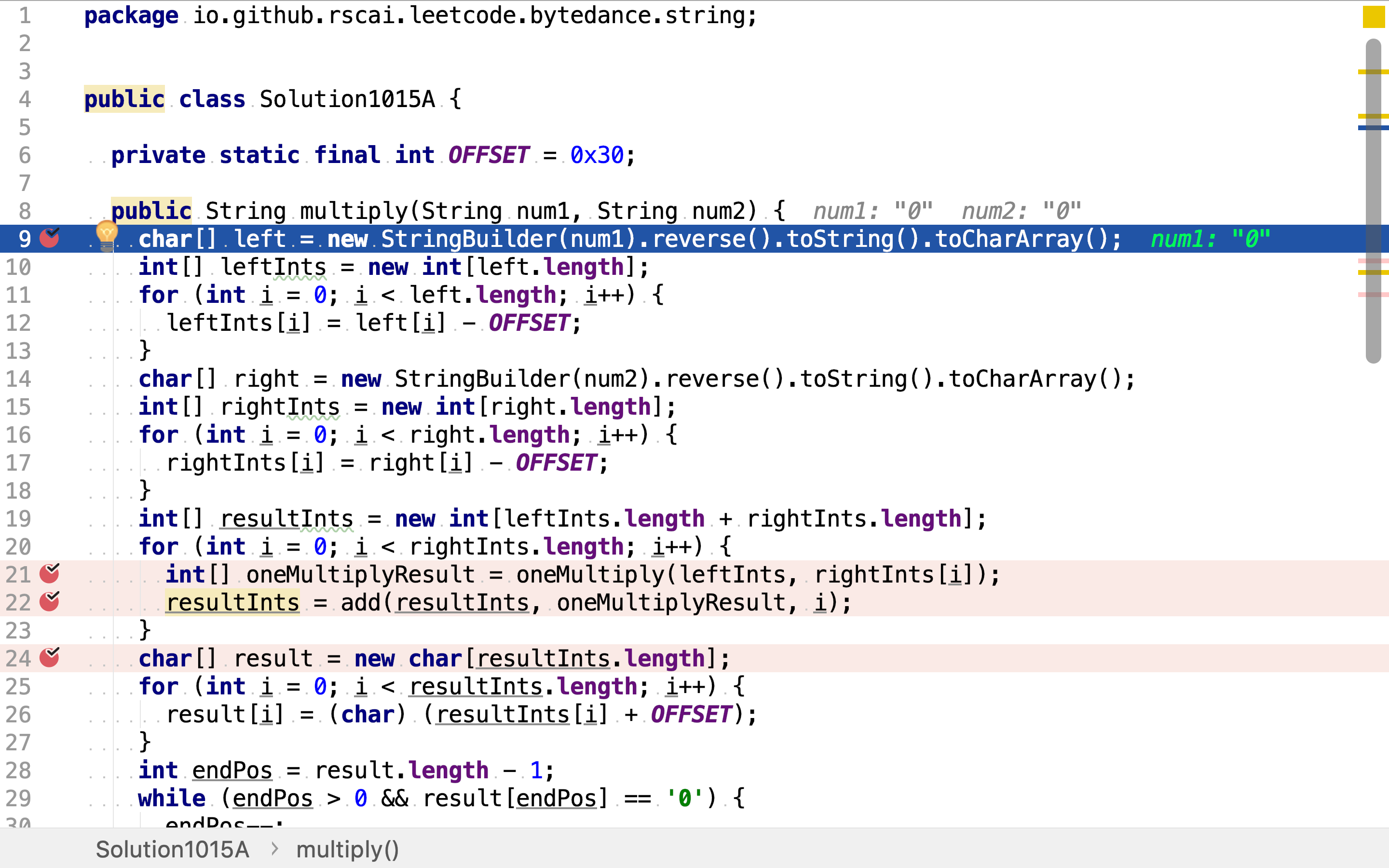
然后,应用「秉法分配律」将第二个乘数拆解为多个整数相加的多项式,再用多项式中的每一项分别乘第一个乘数。将得到的结果再累加起来。
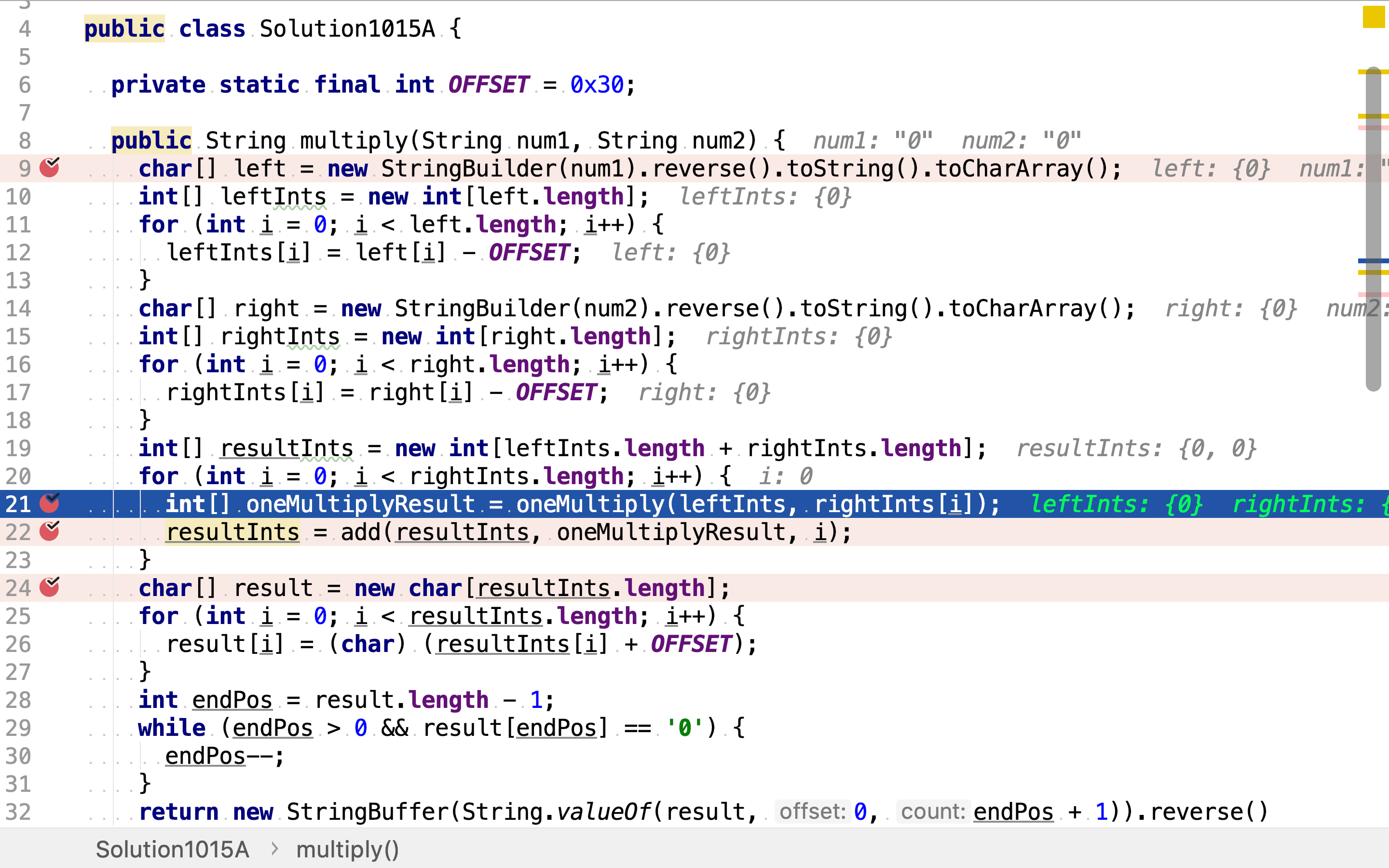
最后,再加整数数组形式的结果转化为字符串形式。
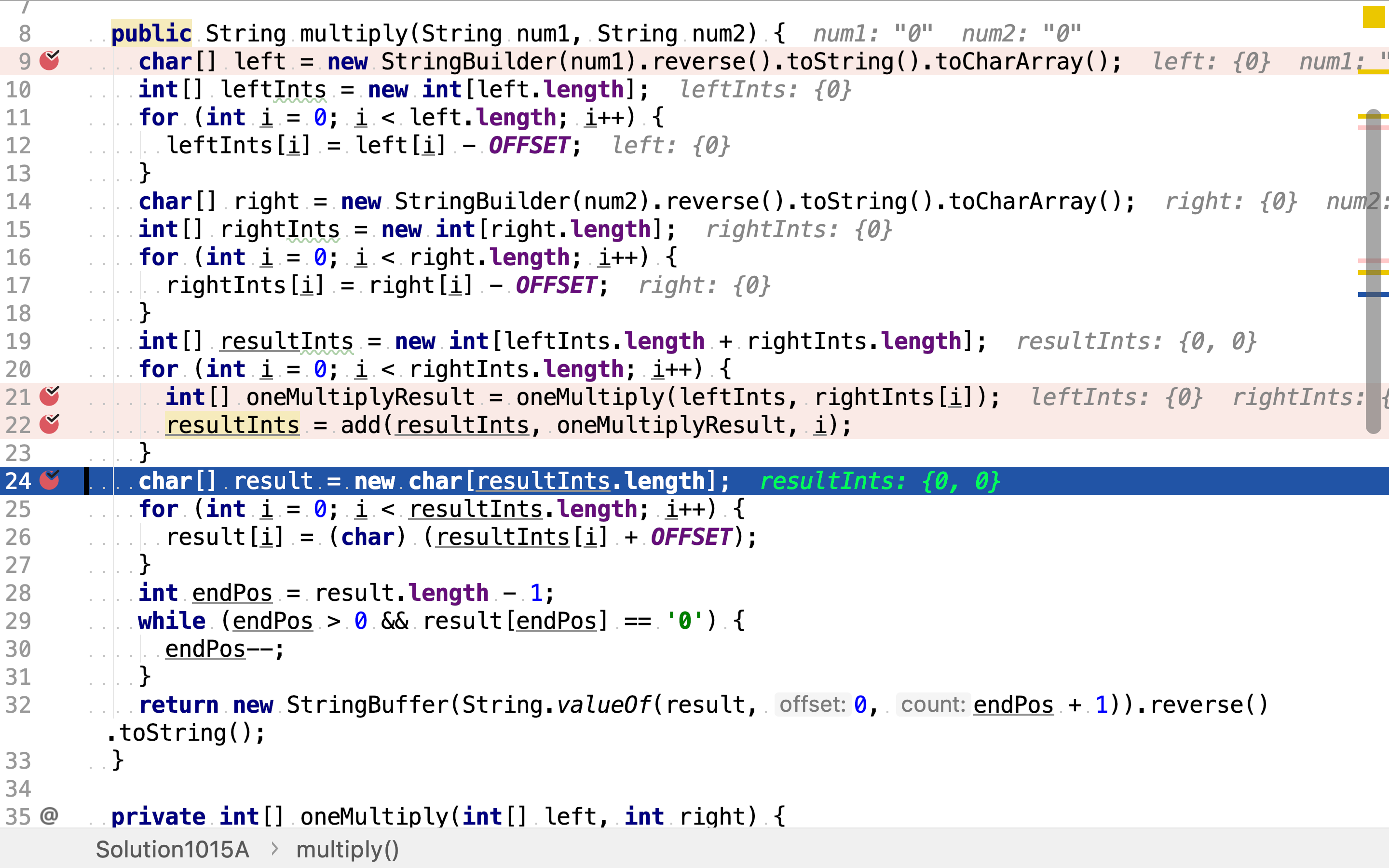
用一位整数乘多位整数时,用一位整数逐位乘多位整数中的每一位,若值大于10则进位,模10后的结果为当前位的结果。
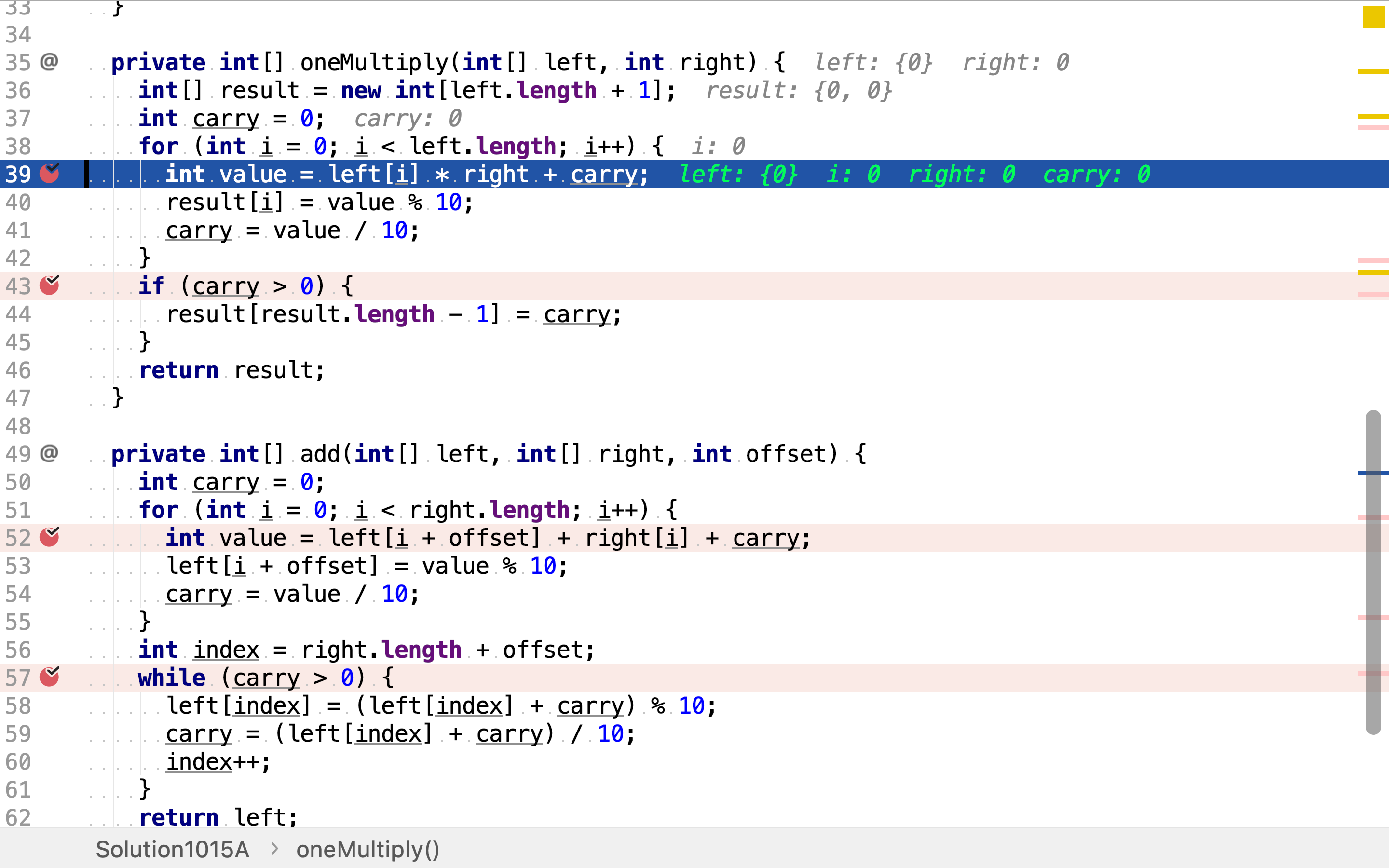
累加单项乘结果是要考虑级数和进位。
复杂度分析
时间复杂度
假设两个乘数位数都是n,则需执行n次oneMultiply和add。每次oneMultiply需用一位整数去乘第一个n位乘数中的每一位。每次add都需逐次累加n位整数的每一位。所以,整体时间复杂度为。
空间复杂度
空间复杂度为。