最大正方形
题目
在一个由 0 和 1 组成的二维矩阵内,找到只包含 1 的最大正方形,并返回其面积。
示例:
输入:
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0
输出: 4
穷举法
一个正方形由四条边确定,对应到二维数组,就是起、止行和起止列确定。
- 起始行从第零行(数组下标从零开始)到最后一行皆可
- 终止行可以是起始行及后续行中的任意一行
- 起始列从第零列到最后一列皆可
- 终止列可以是起绐列及后续列中的任意一行。但其与起始列之间的距离一定等于起始行与终止行之间的距离相等。(正方形定义决定四条边长度相等。)
代码
package io.github.rscai.leetcode.bytedance.dynamic;
public class Solution1028A {
public int maximalSquare(char[][] matrix) {
int maxSideLength = 0;
for (int rowStart = 0; rowStart < matrix.length; rowStart++) {
for (int rowEnd = rowStart + 1; rowEnd < matrix.length + 1; rowEnd++) {
int sideLength = rowEnd - rowStart;
for (int colStart = 0; colStart < matrix[rowStart].length - sideLength + 1; colStart++) {
int colEnd = colStart + sideLength;
if (isSquare(matrix, rowStart, rowEnd, colStart, colEnd)) {
if (sideLength > maxSideLength) {
maxSideLength = sideLength;
}
}
}
}
}
return maxSideLength * maxSideLength;
}
private boolean isSquare(char[][] matrix, int rowStart, int rowEnd, int colStart, int colEnd) {
for (int row = rowStart; row < rowEnd; row++) {
for (int col = colStart; col < colEnd; col++) {
if (matrix[row][col] != '1') {
return false;
}
}
}
return true;
}
}
首先,从0开始罗列所有起始行。
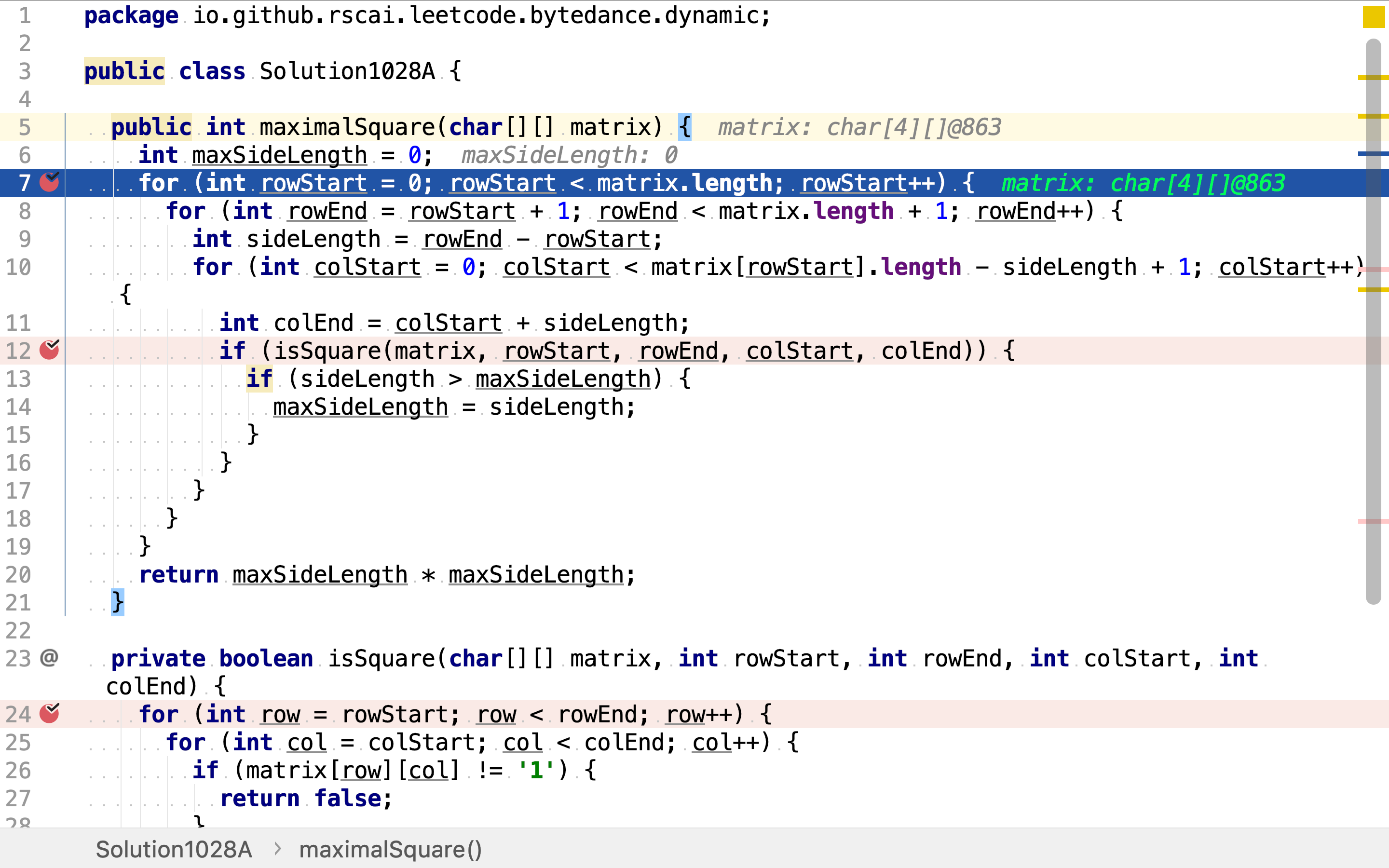
然后,从起始行开始罗列所有终止行。代码中使用左闭右开格式,即行区间是包含起始行下标,但不包终止行下标。比如(0,3),表示包含的行是0, 1, 2。
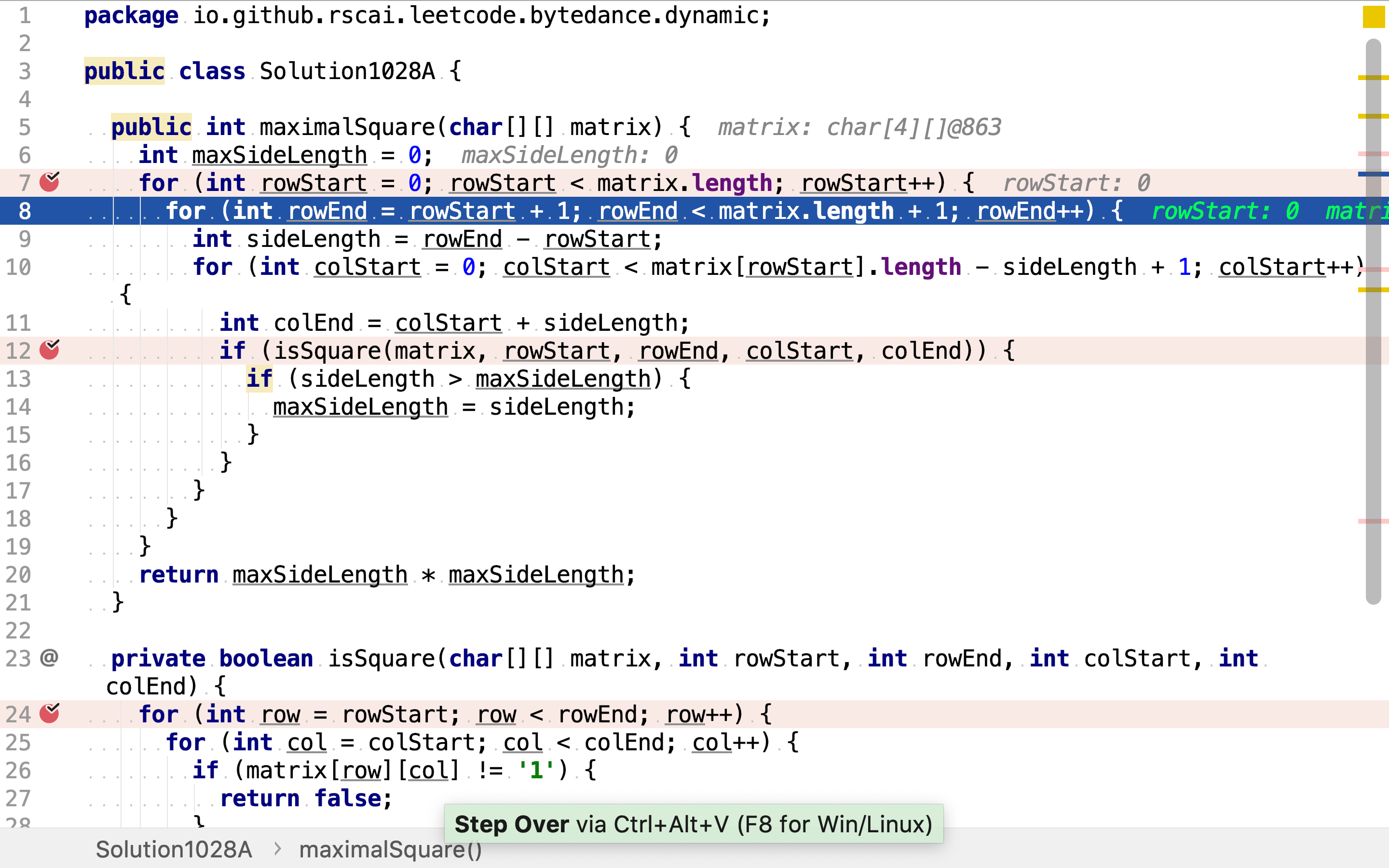
再然后,从0开始罗列所有起始列。
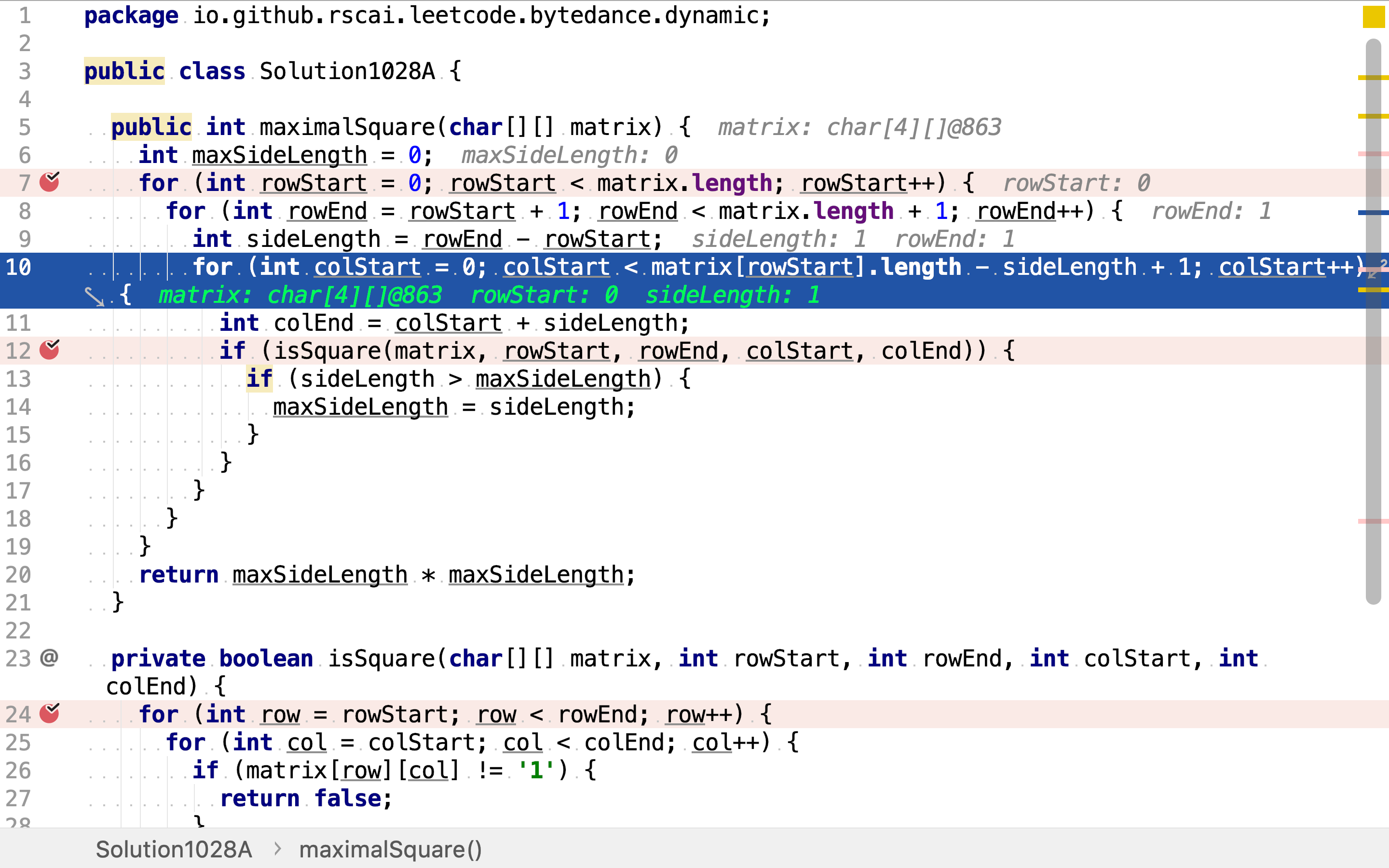
因为正方形的定义,行列区间长度是相等的。所以,当起止行和起始列确定时,终止列也确定了。
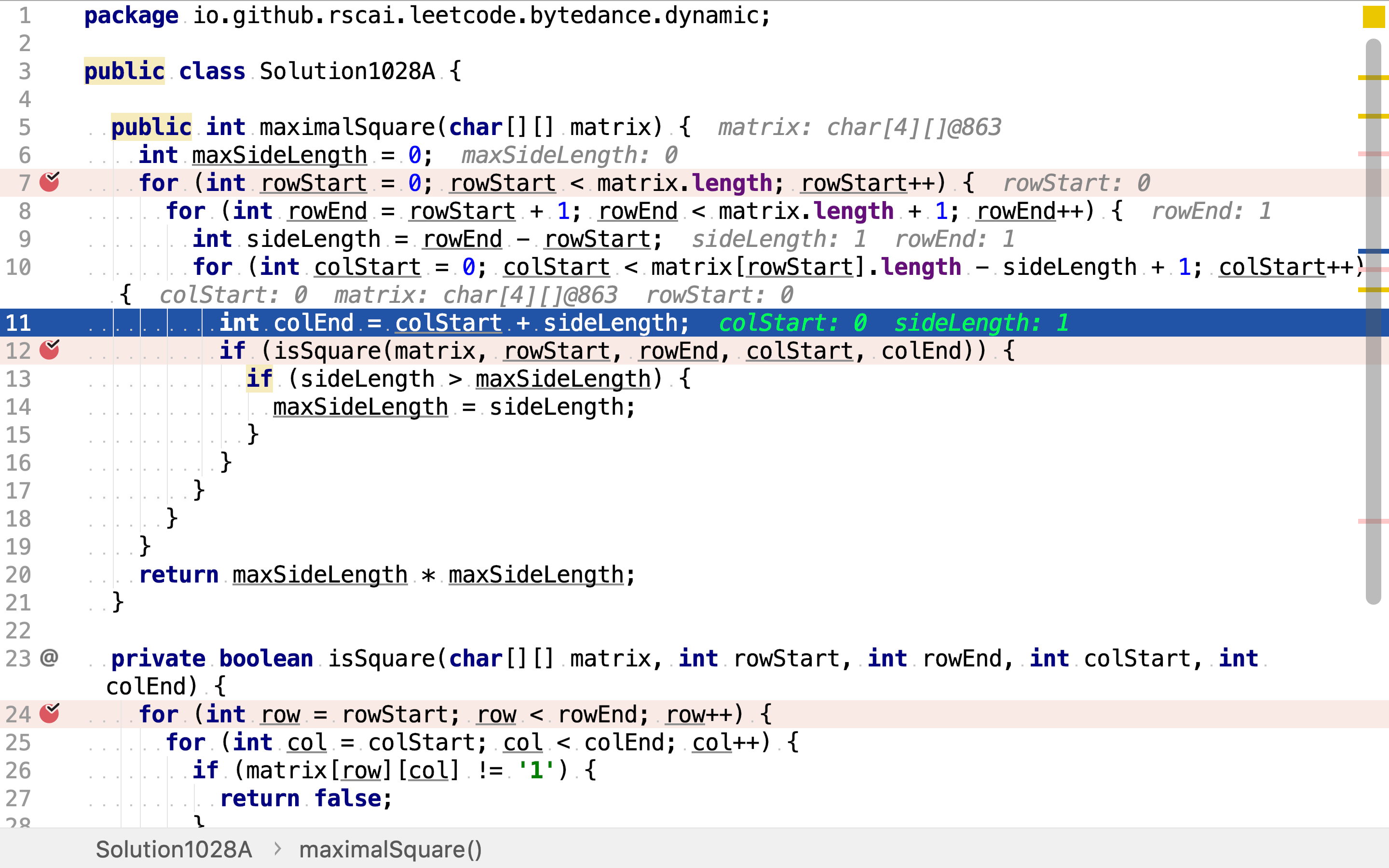
最后,检测每个正方形包含的值是不是都是1。如果是则其是一个所求的正方形。再与之间已找到的最大正方形边长进行比较。
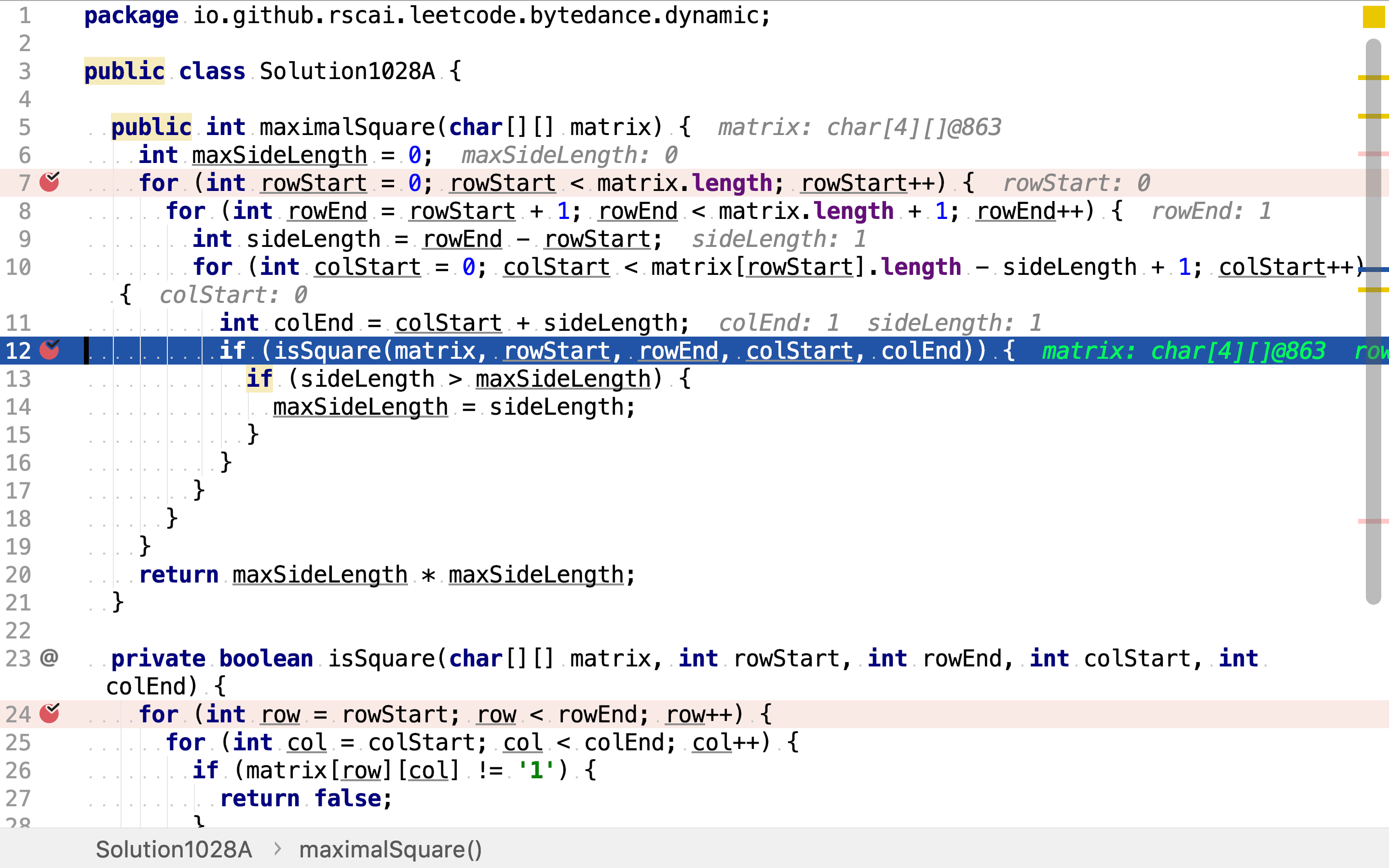
逐一检测正方形所包含的值就可以判断其是否是所求正方形。
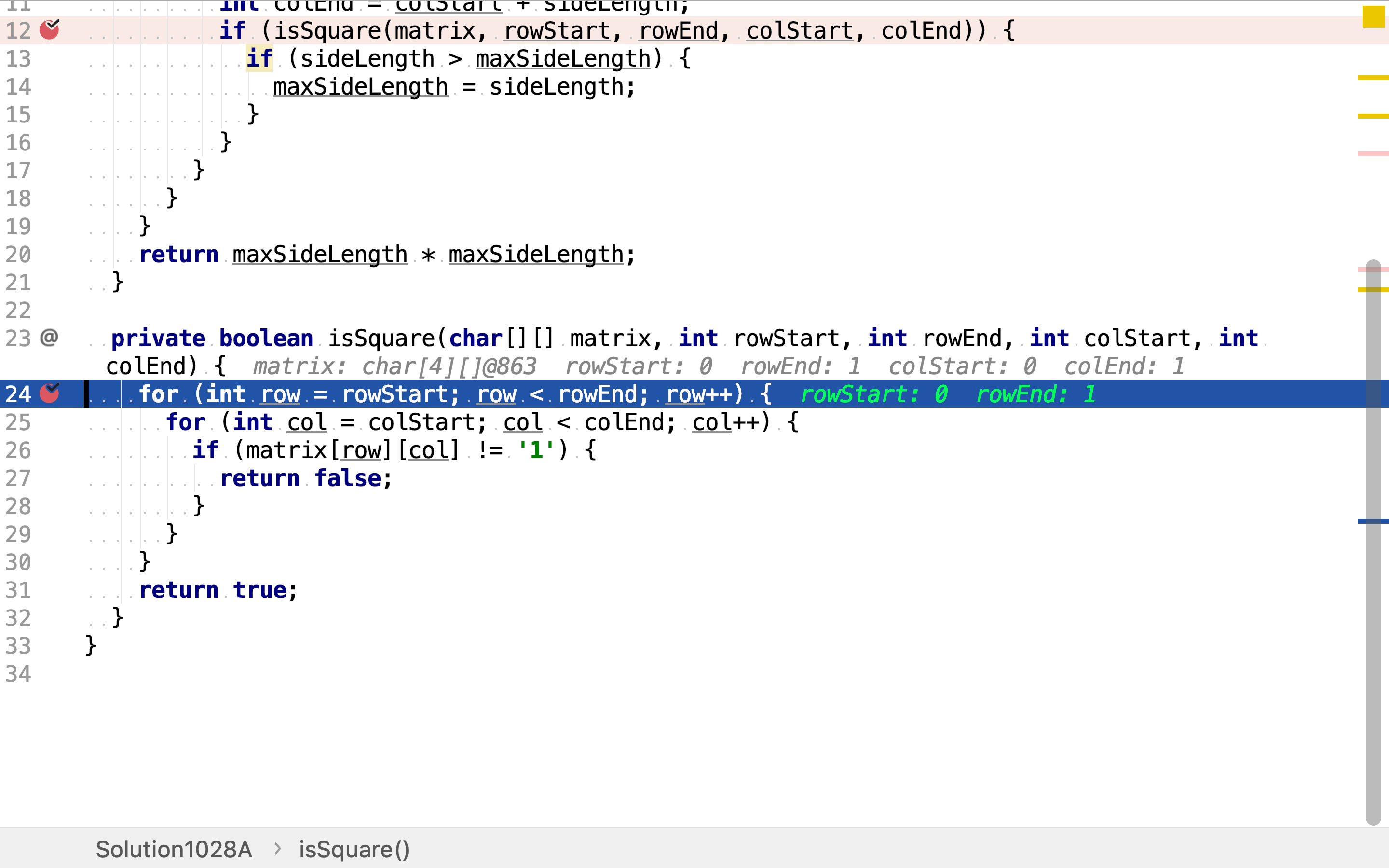
复杂度分析
时间复杂度
时间复杂度是:
空间复杂度
使用了六个变量,空间复杂度是:
动态规划法
「动态规划法」一般形式就是:
- 将一个问题拆分为若干个更小的问题
- 解决若干个更小的问题
- 将若干个更小的问题归併为一个大问题的解
- 若干个更小的问题可以继续拆分,直至问题足够小
正方形有且仅有一个左上⻆,以每一个点为左上⻆的最大正方形所组成的集合一定包含了全局最大正方形。所以,先逐一求出每个点为左上⻆的最大正方形,再一次遍历求出其中最大的正方形。
以左上⻆第一个点(0, 0)为左上⻆的最大正方形有三种情形:
- 边长为0,因为左上⻆第一个点值为0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
- 边长为1,左上⻆第一个点为1但右方
(0, 1),下方(1, 0)和右下方(1, 1)三个点都是0
1 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
- 边长为以右方点
(0, 1),下方点(1,0)和右下方点(1,1)为左上⻆点的最大正方形中最小边长加1
1 1 1 0
1 1 1 1
1 1 1 1
0 1 1 1
第二种情形可以合併到第三种情形,正方形左上⻆第一个点是0等同于边长为为0的正方形。
依此类推,以点(0, 1)为左上⻆的最大正方形:
- 边长为0,如果点
(0, 1)的值为0
- 边长为以右方点(0, 2)
、下方点(1, 1)和右下方点(1, 2)`为左上⻆的最大正方形中最小边长加1
用函数符号表示。为横坐标,取值范围。为从坐木田一火,取值范围。为点(r, c)的值,取值范围。为以点(r, c)为左上⻆的最大正方形边长。则:
将函数的调用以树状形式展示出来,可以发现有很多函数值为重用使用。这𥚃可以缓存重用函数值,以大幅减少计算量。
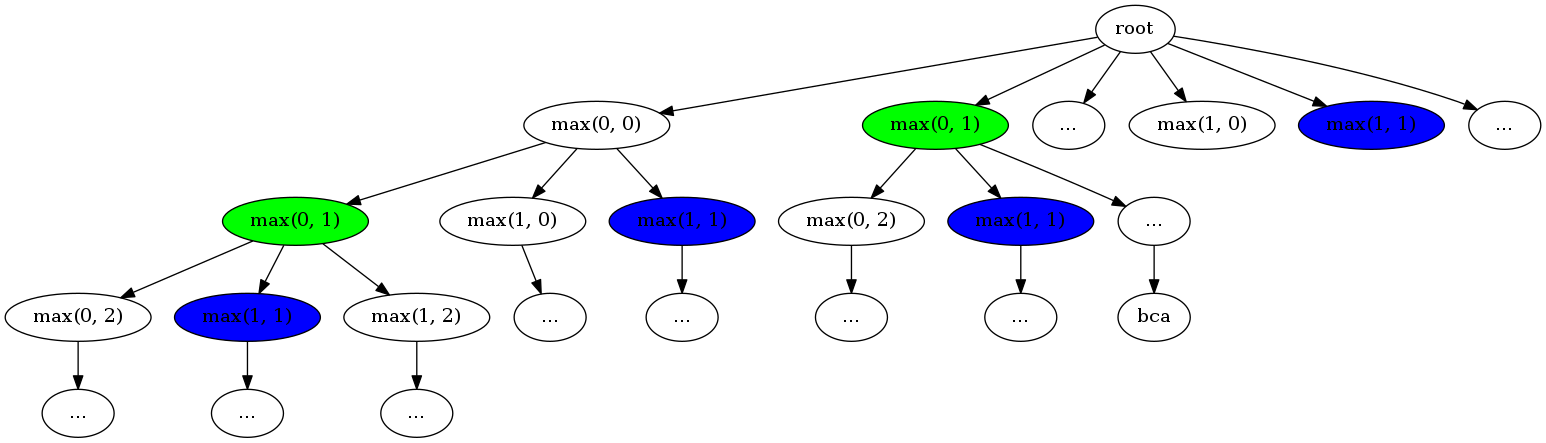
代码
package io.github.rscai.leetcode.bytedance.dynamic;
import java.util.HashMap;
import java.util.Map;
import java.util.function.BiFunction;
public class Solution1028B {
public int maximalSquare(char[][] matrix) {
BiFunction<Integer, Integer, Integer> maxSideLengthStartAt = new BiFunction<Integer, Integer, Integer>() {
private Map<String, Integer> cache = new HashMap<>();
@Override
public Integer apply(Integer row, Integer col) {
String key = String.format("%d-%d", row, col);
if (cache.containsKey(key)) {
return cache.get(key);
}
Integer result = doApply(row, col);
cache.put(key, result);
return result;
}
private Integer doApply(Integer row, Integer col) {
if (row >= matrix.length || col >= matrix[row].length) {
return 0;
}
if ('0' == matrix[row][col]) {
return 0;
}
return 1 + Math
.min(apply(row + 1, col + 1),
Math.min(apply(row + 1, col),
apply(row, col + 1)));
}
};
int maxSideLength = 0;
for (int row = 0; row < matrix.length; row++) {
for (int col = 0; col < matrix[row].length; col++) {
int sideLength = maxSideLengthStartAt.apply(row, col);
if (sideLength > maxSideLength) {
maxSideLength = sideLength;
}
}
}
return maxSideLength * maxSideLength;
}
}
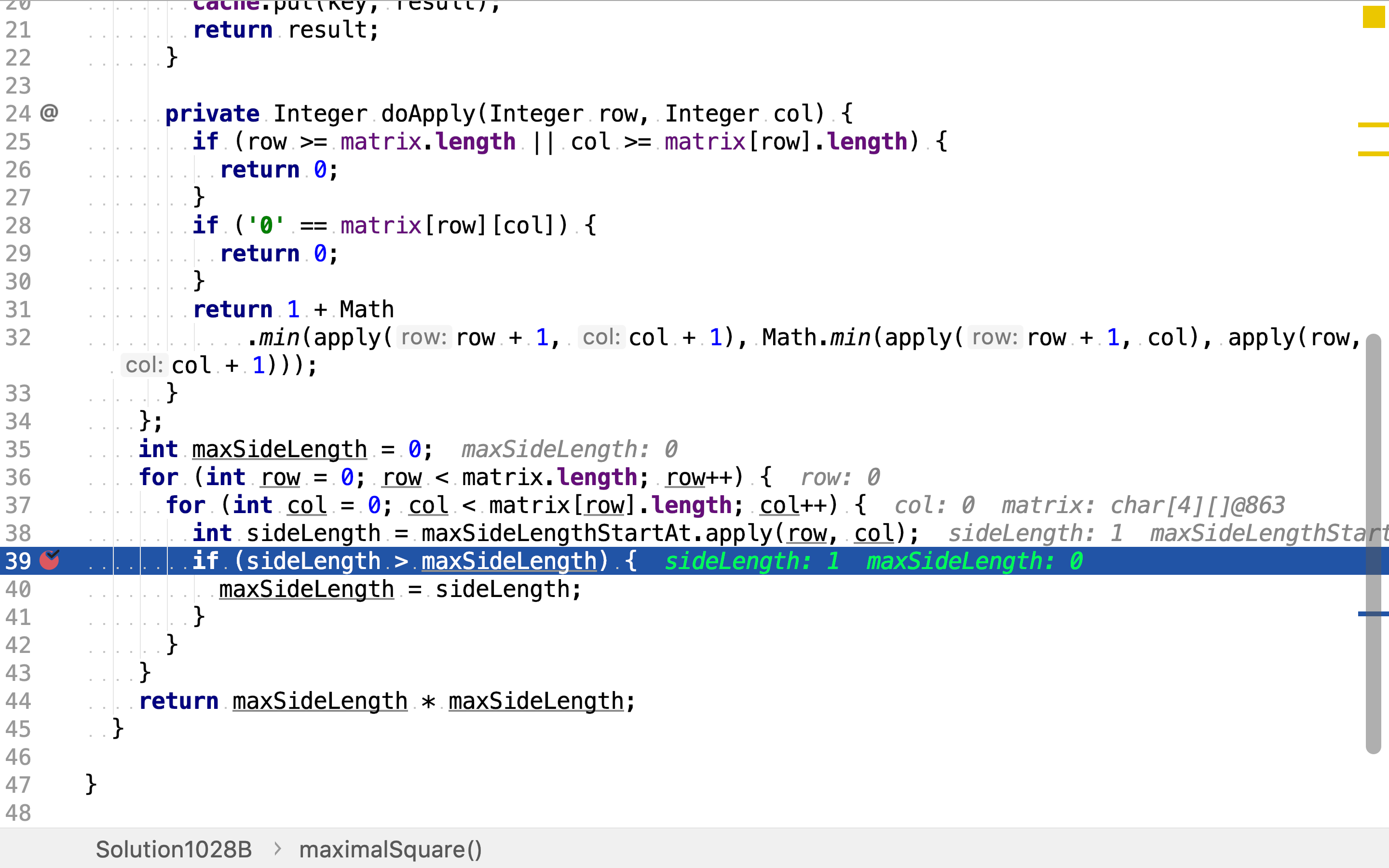
首先,逐一求出以每个点为左上⻆的最大正方形边长。
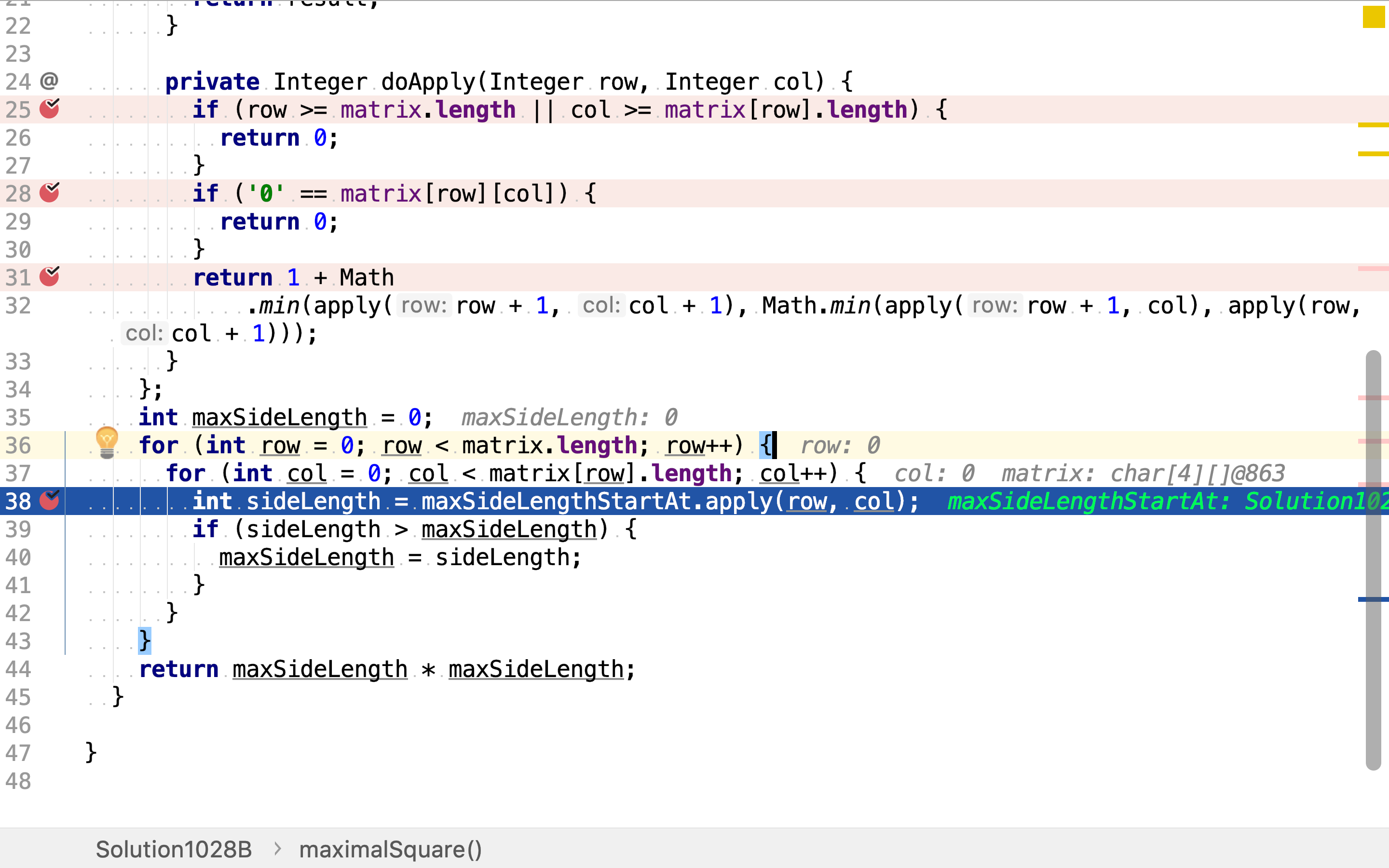
然后,再求出最大边长。
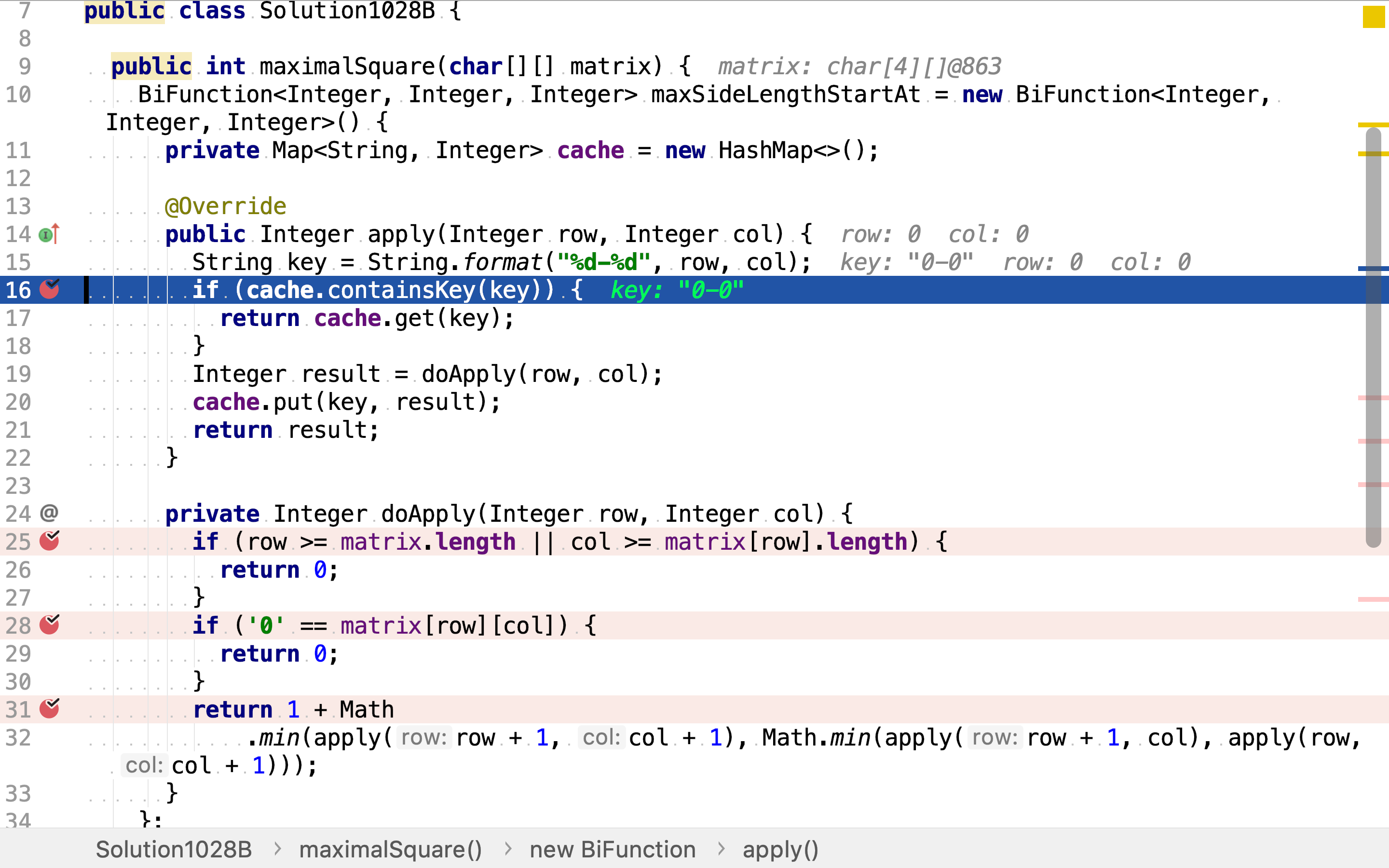
其缓存了以某个点为左上⻆最大正方形边长的值,在计算以某个点为左上⻆最大正方形边长时,先检索是否已缓存了值。
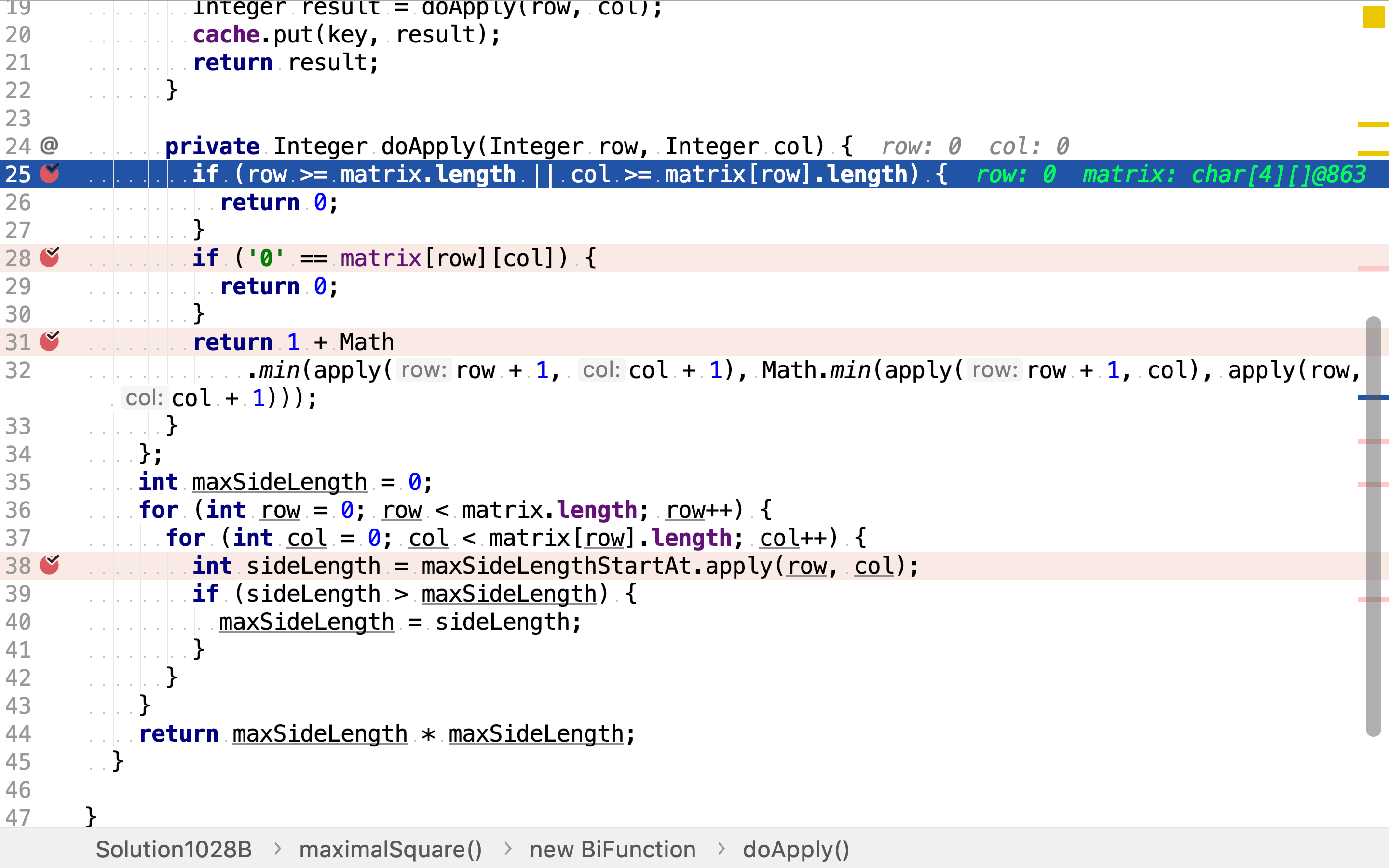
若无缓存,则计算之。这𥚃有三种情况:
- 轮入点超出了矩阵,其值一定是0。
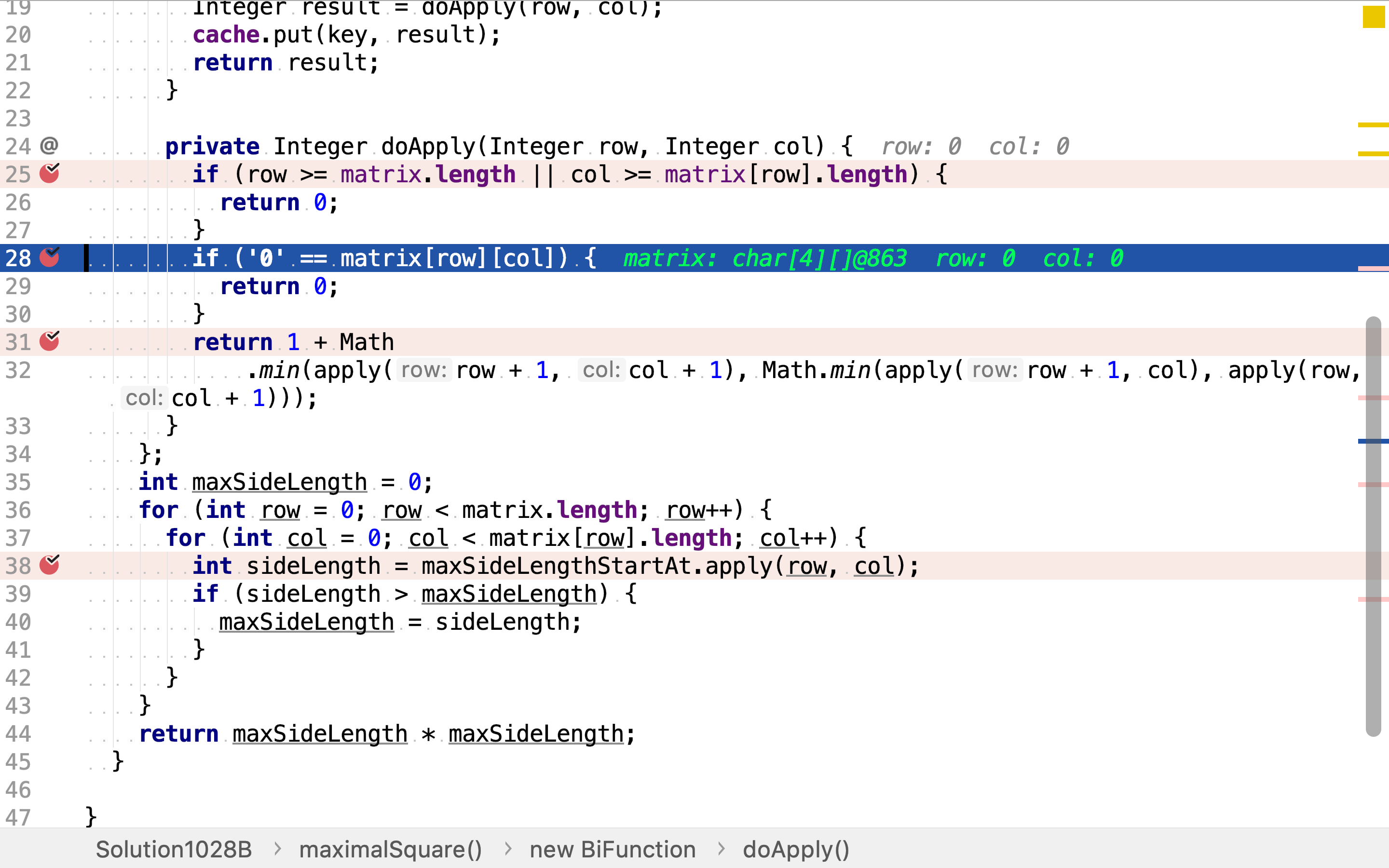
- 轮入点的值为0,则以其为左上⻆的最大正方形边长为0。
- 轮入点的值为1,则以其为左上⻆的最大正方形边长为以右方点、下方点和右下方点为左上⻆的最大正方形边长中最小的值加1。
复杂度分析
时间复杂度
所有拆分出来的子问题都求以矩阵中某一点为轮入的函数值,且函数值都被缓存重用。所以实际上其只做了跟矩阵大小相当的计算。时间复杂度为:
空间复杂度
其缓存了所有的轮入的函数值。空间复杂度为:
一次遍历实现动态规划
上面的递归实现可以使用一次循环实现。
package io.github.rscai.leetcode.bytedance.dynamic;
public class Solution1028C {
public int maximalSquare(char[][] matrix) {
int rows = matrix.length;
if (rows == 0) {
return 0;
}
int cols = matrix[0].length;
if (cols == 0) {
return 0;
}
int maxSideLength = 0;
int[][] maxSideLengths = new int[rows][cols];
for (int row = rows - 1; row >= 0; row--) {
for (int col = cols - 1; col >= 0; col--) {
if ('1' == matrix[row][col]) {
int maxSideLengthOfRight = 0;
int maxSideLengthOfDown = 0;
int maxSideLengthOfRightDown = 0;
if (col + 1 < cols) {
maxSideLengthOfRight = maxSideLengths[row][col + 1];
}
if (row + 1 < rows) {
maxSideLengthOfDown = maxSideLengths[row + 1][col];
}
if (col + 1 < cols && row + 1 < rows) {
maxSideLengthOfRightDown = maxSideLengths[row + 1][col + 1];
}
int maxSideLengthAtCurrent = 1 + Math
.min(maxSideLengthOfRight, Math.min(maxSideLengthOfDown, maxSideLengthOfRightDown));
maxSideLengths[row][col] = maxSideLengthAtCurrent;
if (maxSideLengthAtCurrent > maxSideLength) {
maxSideLength = maxSideLengthAtCurrent;
}
}
}
}
return maxSideLength * maxSideLength;
}
}












