最小栈

题目

设计一个支持 push，pop，top 操作，并能在常数时间内检索到最小元素的栈。

• push(x) -- 将元素 x 推入栈中。
• pop() -- 删除栈顶的元素。
• top() -- 获取栈顶元素。
• getMin() -- 检索栈中的最小元素。

示例:

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

元素和最小值结对法

将「入栈元素」和「其入栈后栈内最小值」组成一对，入栈、出栈操作都是操作对。

举个例子，创建一个栈，初始为空，不存在最小值。

当压入值-2时，最小值变为-2。所以同时压入值-2和最小值-2。

当压入值0，最小值依旧为-2。所以同时压入值0和最小值-2。

当压入值-3时，最小值变为-3。所以同时压入值-3和最小值-3。

将值和最小值结对压入栈，保证栈顶元素就是最小值。

当弹出元素时，将值和最小值一同弹出。之前最小值从-2变为-3是因为值-3的加入，现在-3被移出栈了，最小值也就回复到之前的-2。

代码实现

使用JDK提供的ArrayList来实现有序列表，栈就只能在一端增加删除元素的有序列表。

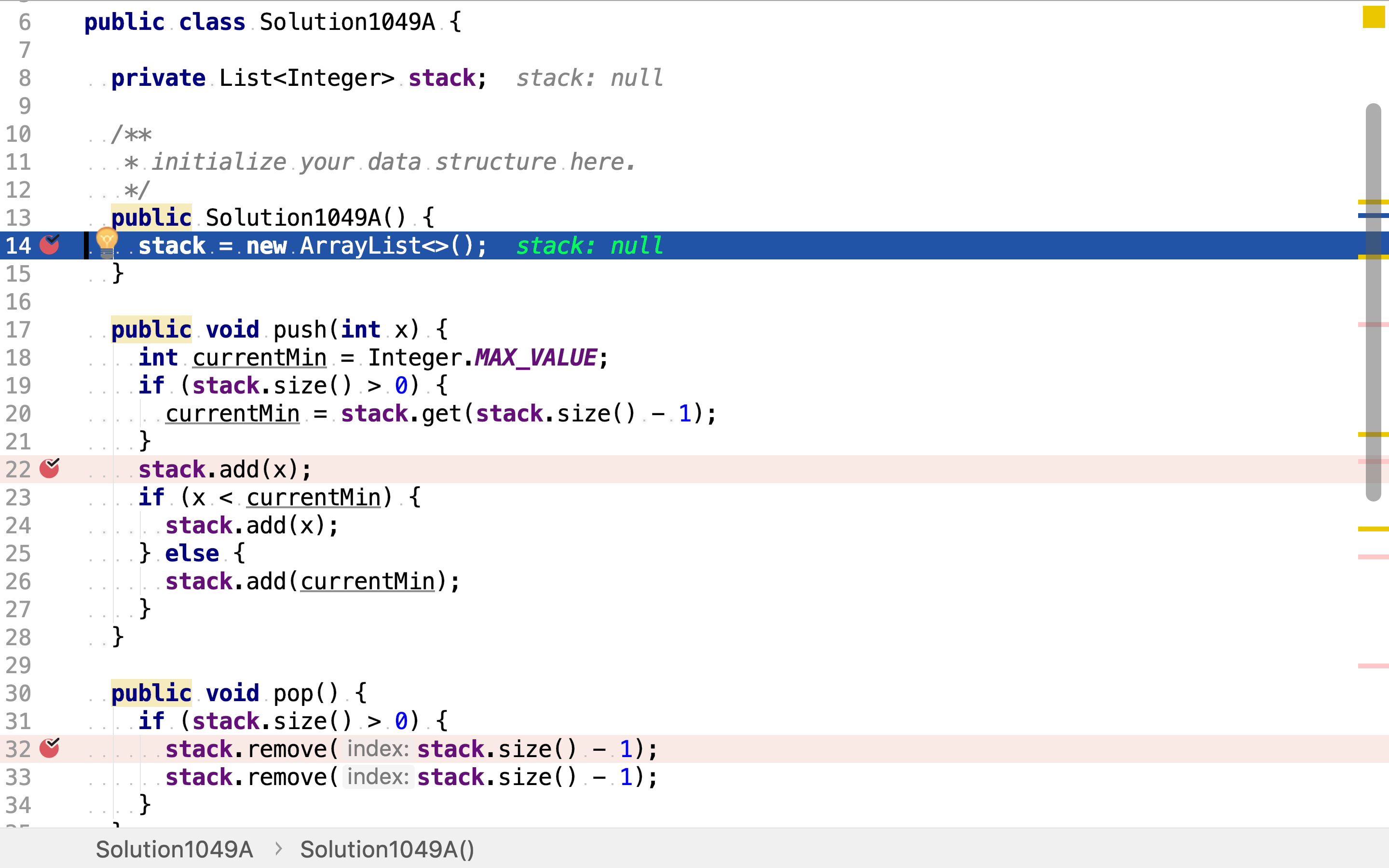
入栈的时候将值和最小值成对入栈。最小值通过取之前最小值和当前压入值之中最小的值得到。

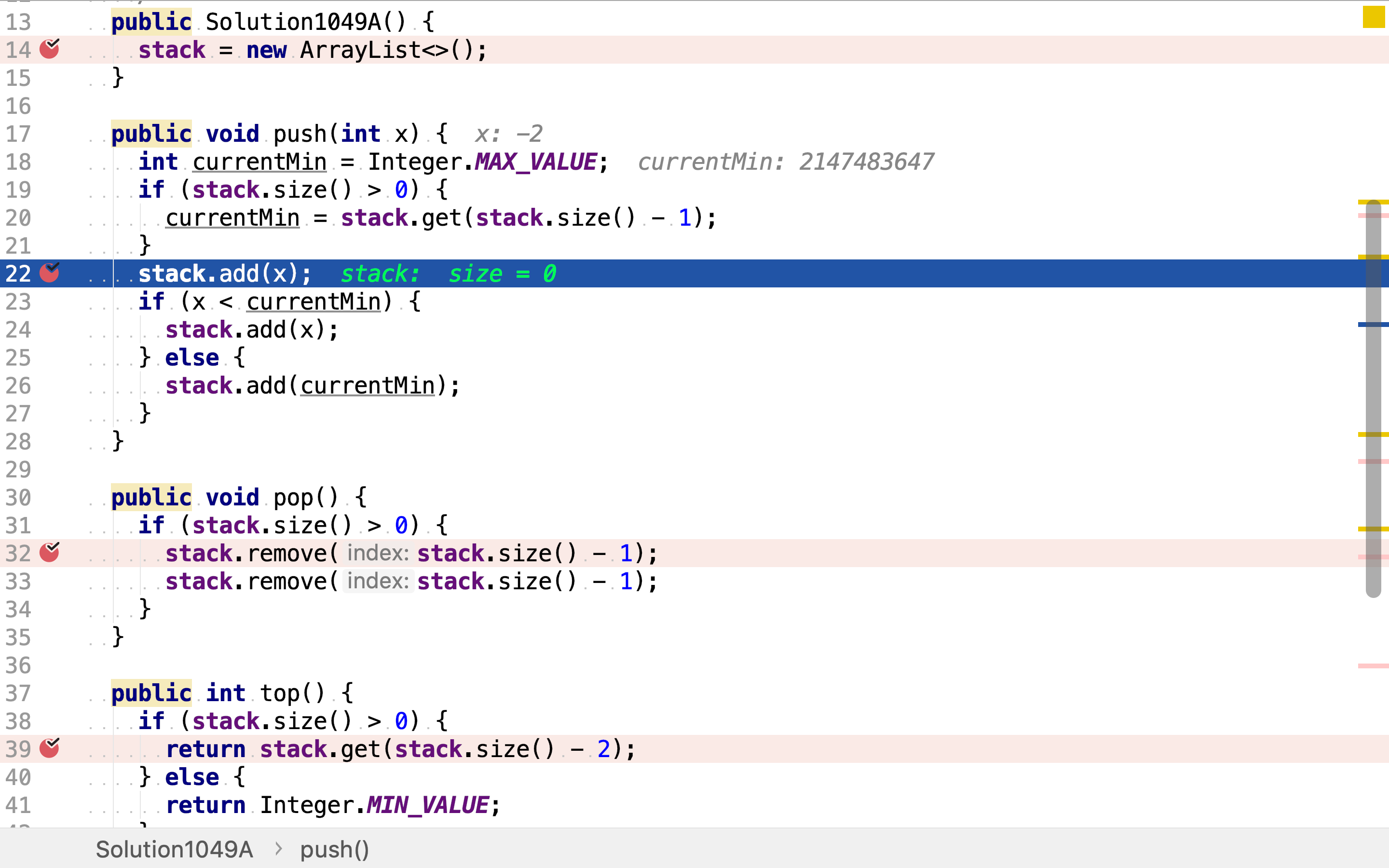
出栈的时候也成对出栈。

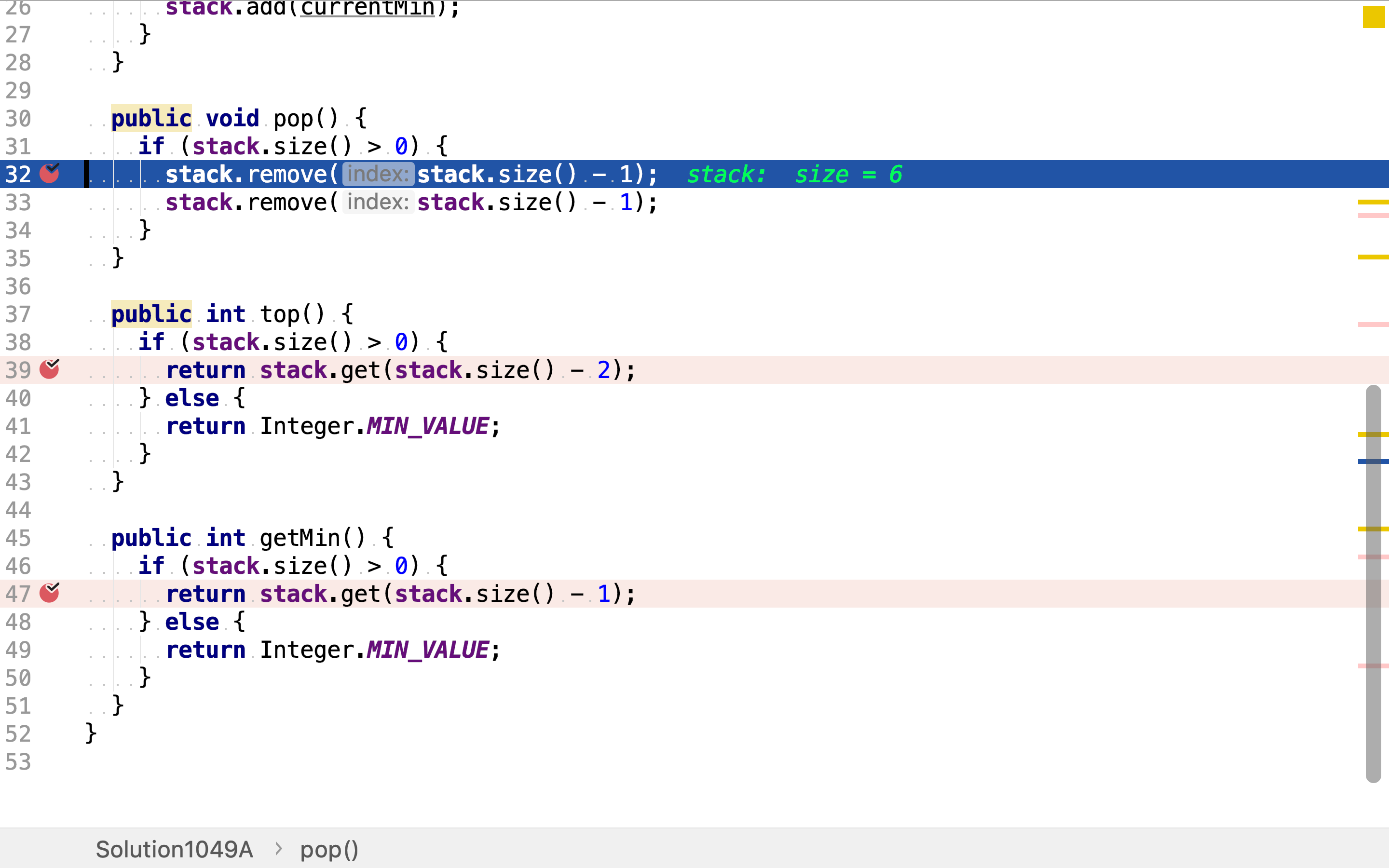
值和最小值是成对压入、弹出的，栈顶元素是最值，从顶往下第二个元素就是罗辑上的「栈顶」元素。

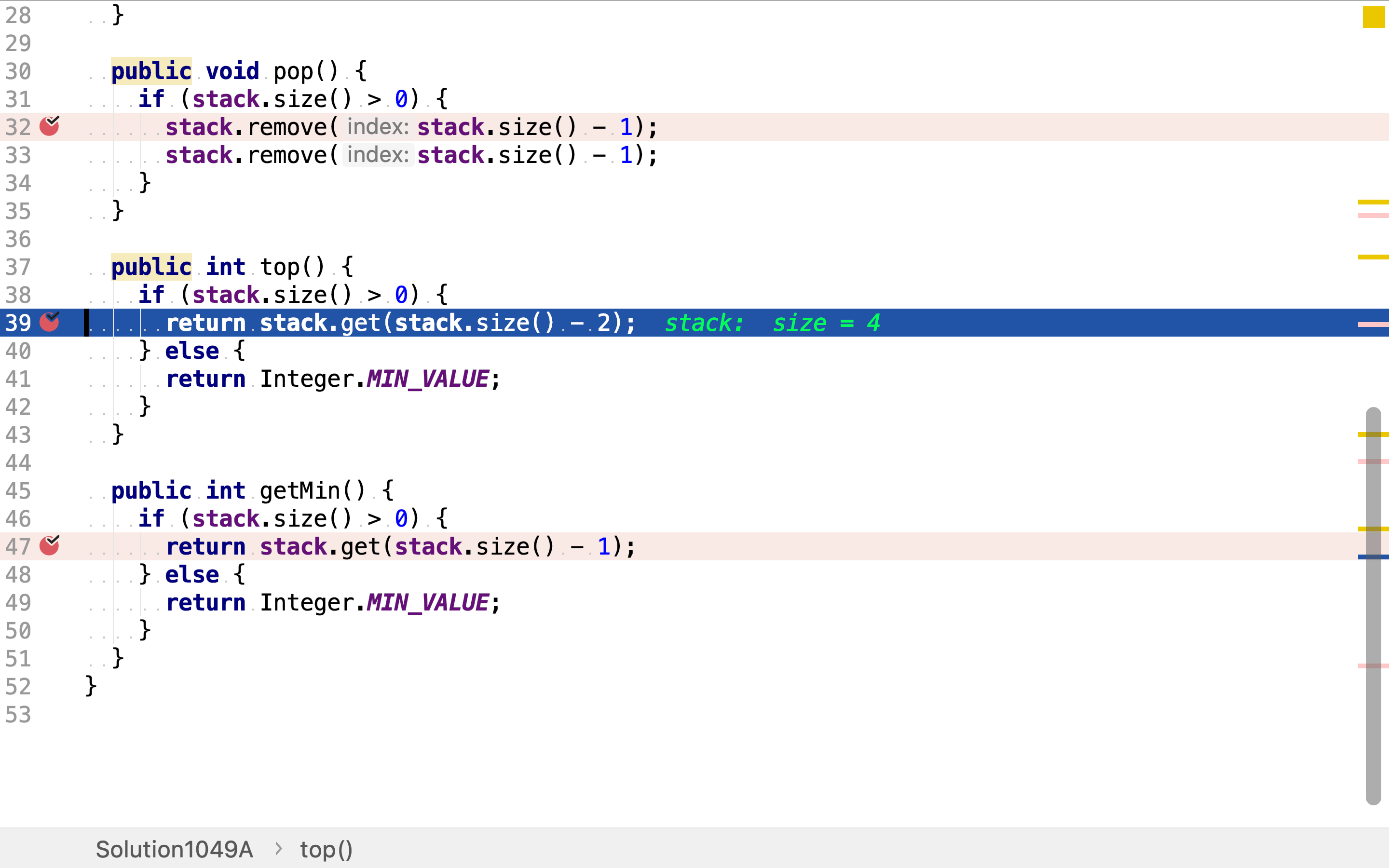
值和最小值是成对压入、弹出的，栈顶元素就是最小值。

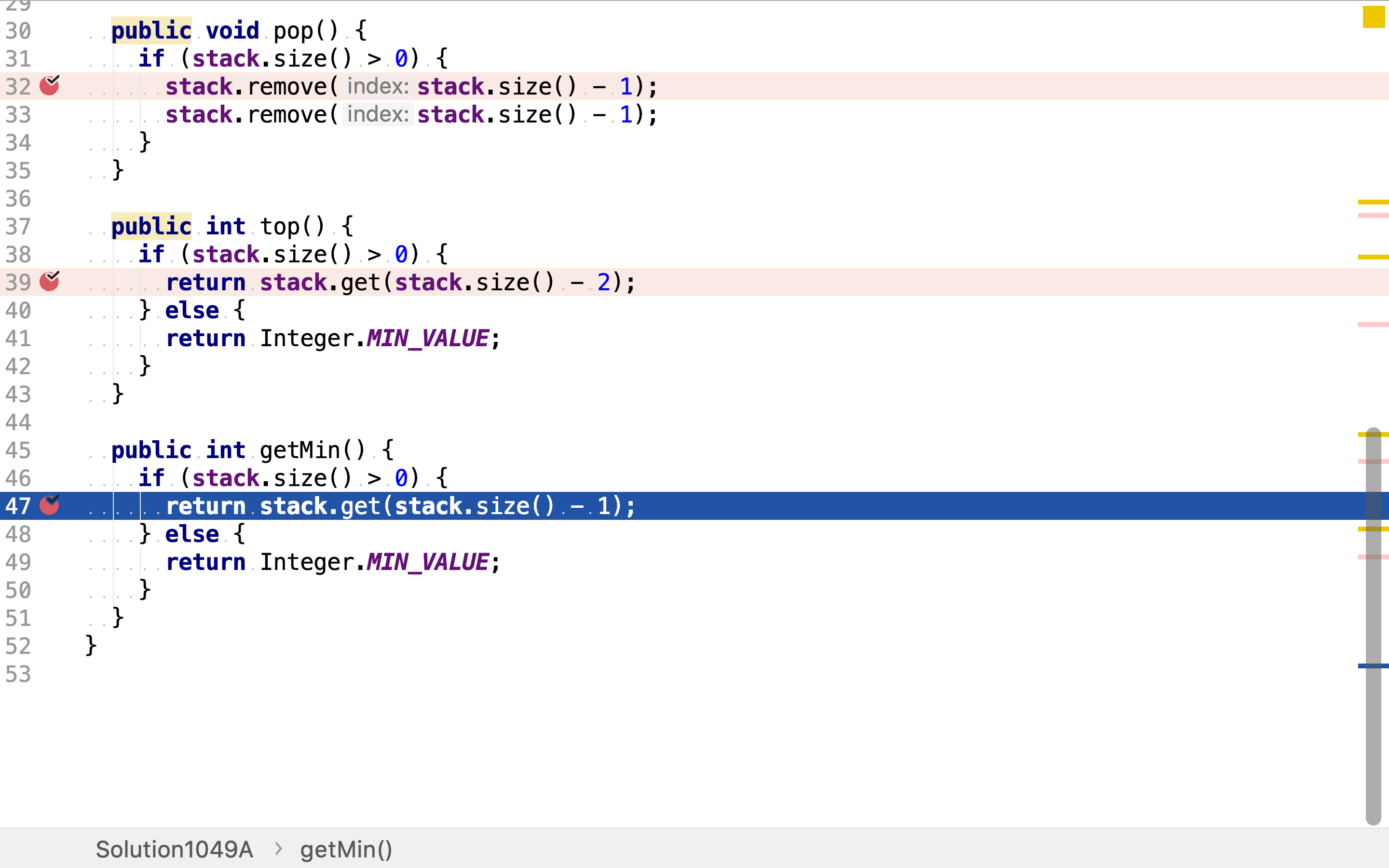
复杂度分析

时间复杂度

push只在栈顶操作，且每次都是固定压入两个元素（值和最小值），跟栈中的数据量无关。所以时间复杂度为$\mathcal{O}(1)$。

pop也只在栈顶操作，且每次都是固定弹出两个元素（值和最小值），跟栈中数据量无关。所以时间复杂度为$\mathcal{O}(1)$。

top固定读取从顶往下第二个元素，跟栈中数据量无关。所以时间复杂度为$\mathcal{O}(1)$。

getMin固定读取栈顶元素，跟栈中数据量无关。所以时间复杂度为$\mtahcal{O}(1)$。

空间复杂度

本结构将每个值都扩展为两个值组成的对，假设值的数据量为$n$，则栈中将有$2n$个元素。空间复杂度为$\mathcal{O}(2n)$，消掉常量为$\mathcal{O}(n)$。

双栈法

创建两个栈，一个用于存储值，另一个用于存储最小值。

举个例子，创建两个栈dataStack和minValueStack。

把值-2压入dataStack时，最小值变为-2，将最小值-2同时压入minValueStack。

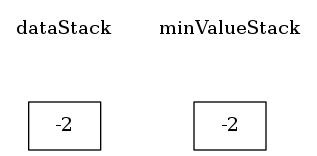
把值0压入dataStack时，最小值没有发生变化，所以就不压入minValueStack。

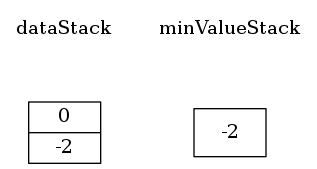
把值-3压入dataStack时，最小值变为-3，所以把-3同时压入minValueStack。

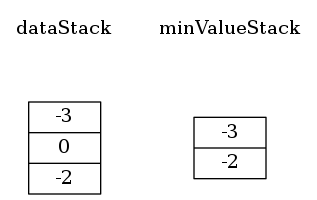
minValueStack栈顶元素就是最小值。

从dataStack弹出值时，要检查minValueStack栈顶元素是否等于dataStack栈顶元素，若是则表明「当前最小值」被移出了dataStack，minValueStack要相应地将其弹出。

代码实现

使用JDK提供的ArrayList实现两个栈，dataStack存储值，minValueStack存储最小值。

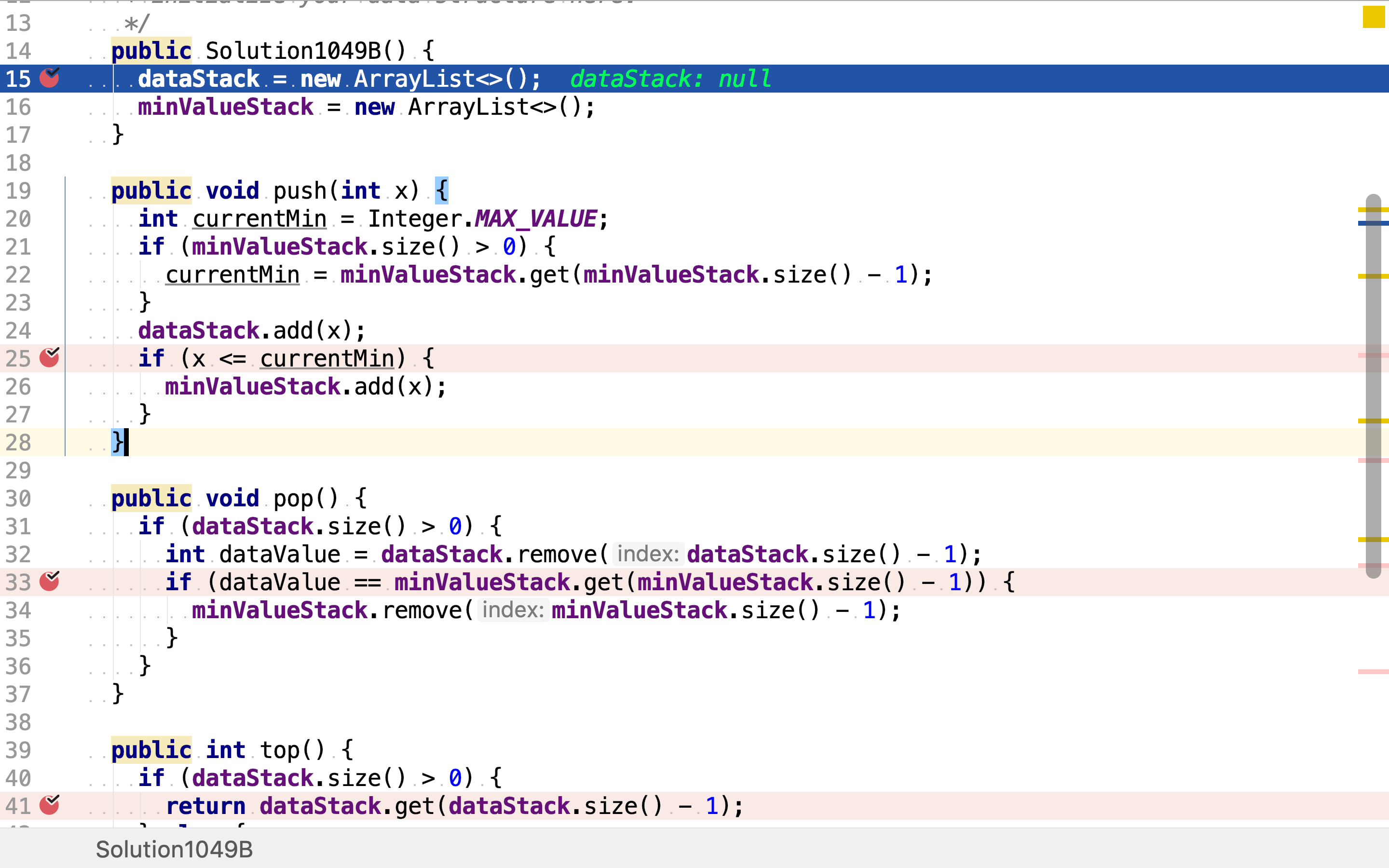
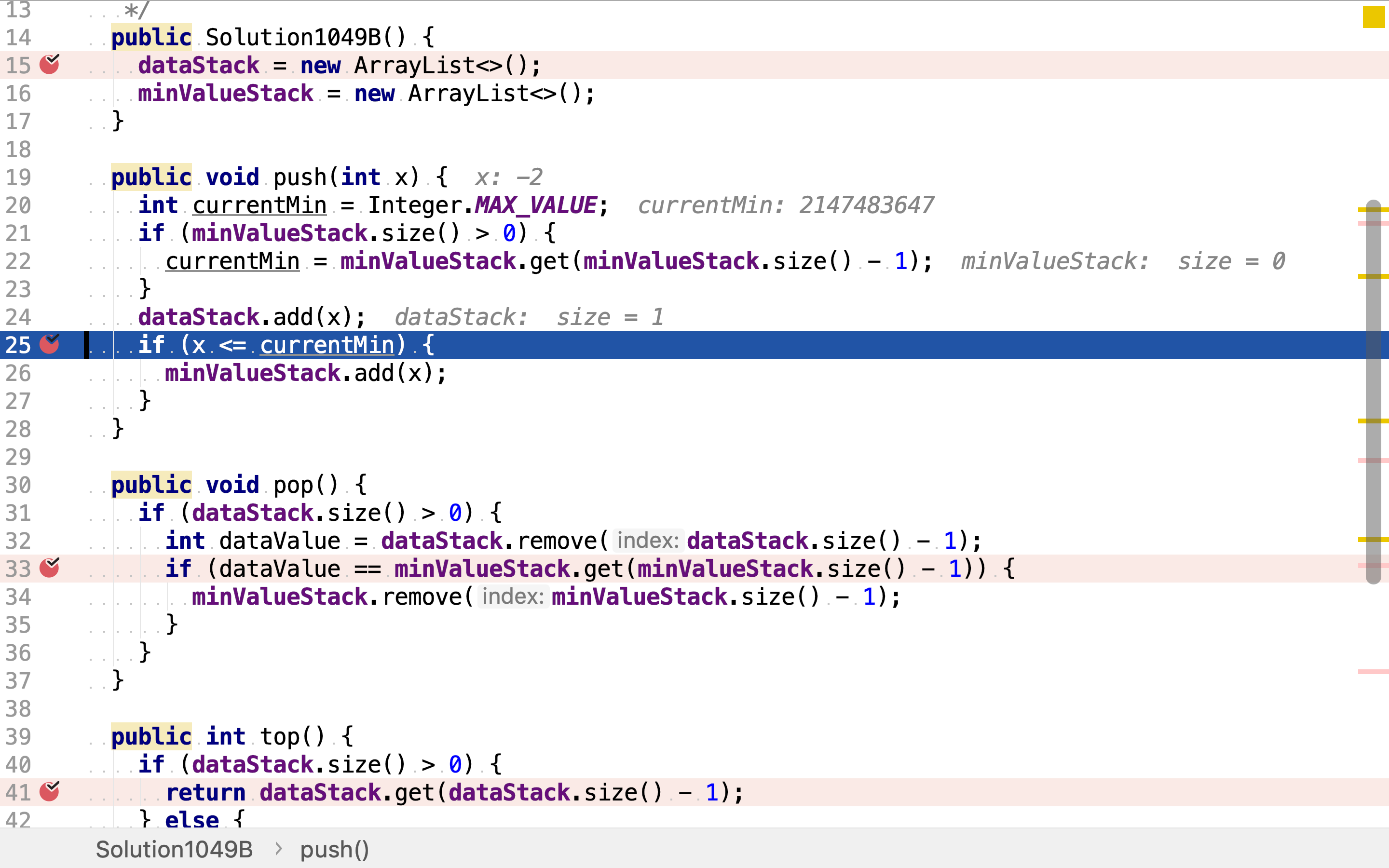
压入值时，先将值压入dataStack，再比较新压入值跟当前最小值。若新压入值小于或等于当前最小值，则最小值被改变，将新值同时压入minValueStack。

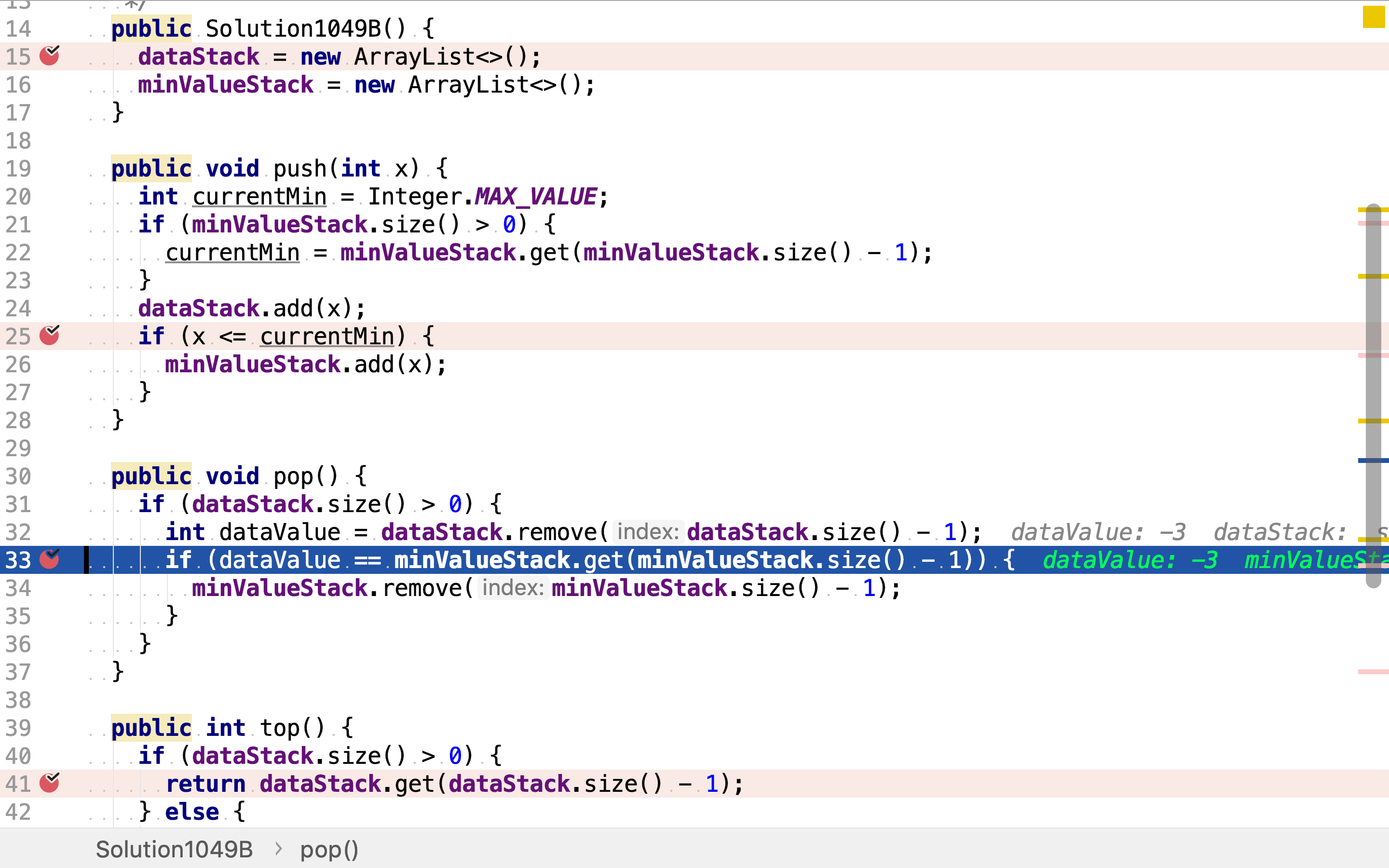
弹出值时，除了将dataStack栈顶元素弹出，同时若minValueStack栈顶元素等于dataStack弹出元素，则意味着minValueStack栈顶的最小值被移除了，所以要同步弹出minValueStack栈顶元素。

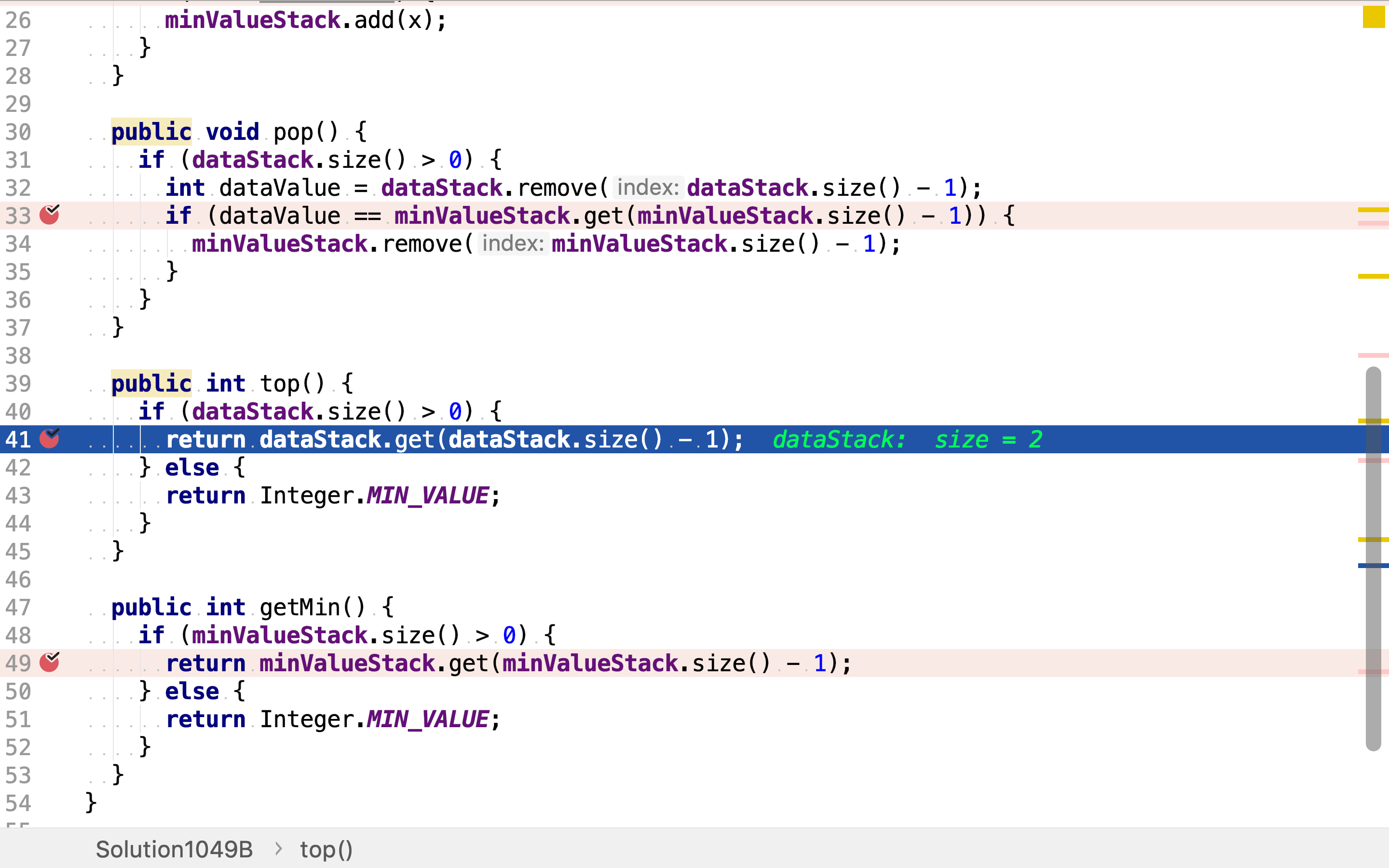
dataStack专门存储值，所以dataStack栈顶元素即即最后压入元素。

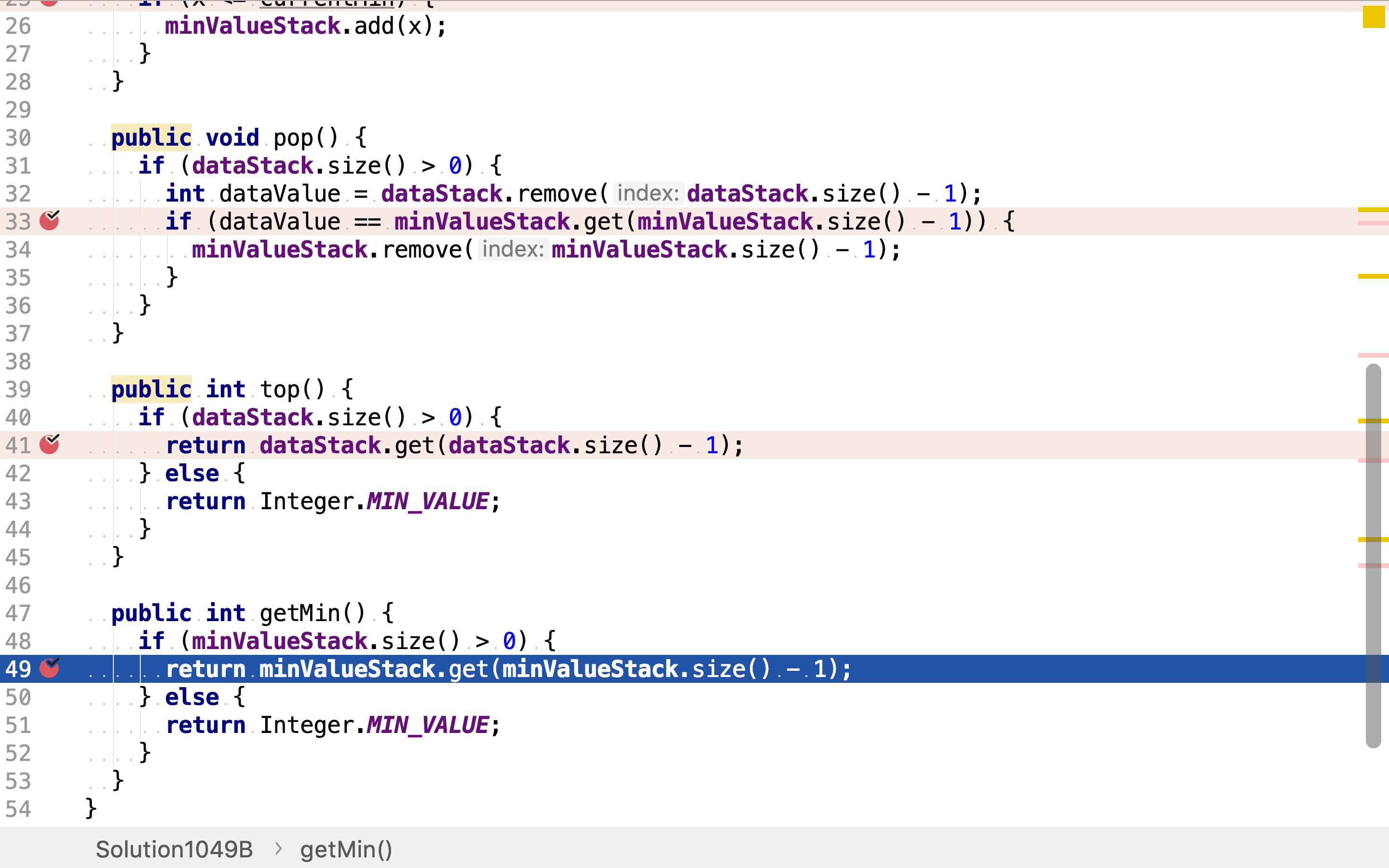
minValueStack专门存储最小值，minValueStack栈顶元素即最小值。

复复杂分析

时间复杂度

push操作最多在两个栈中分别压入一个元素，时间复杂度为$\mathcal{O}(1)$。

pop操作最多从两个栈中分别弹出栈顶元素，时间复杂度为$\mathcal{O}(1)$。

top操作直接从栈dataStack读取栈顶元素，时间复杂度为$\mathcal{O}(1)$。

getMin操作直接从栈minValueStack读取栈顶元素，时间复杂度为$\mathcal{O}(1)$。

空间复杂度

本结构使用两个栈，假设值的数据量为$n$，则dataStack佔用$n$个存储空间，minValueStack最坏情况下（所有值都相等或值以降序顺序压入）佔用$n$个存储空间。总体空间复杂度为$\mathcal{O}(n)$。