相交链表
题目
编写一个程序,找到两个单链表相交的起始节点。
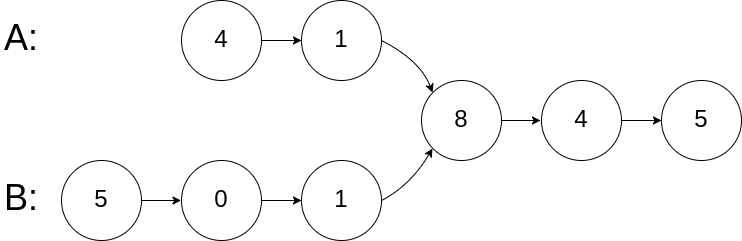
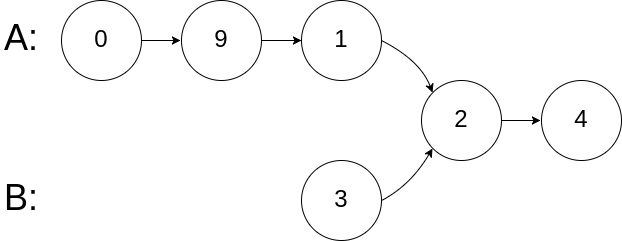
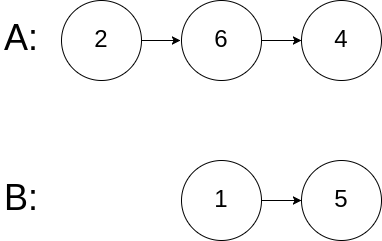
如下面的两个链表:
在节点 c1 开始相交。
示例 1:
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3 输出:Reference of the node with value = 8 输入解释:相交节点的值为 8 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。示例2:
输入:intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1 输出:Reference of the node with value = 2 输入解释:相交节点的值为 2 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [0,9,1,2,4],链表 B 为 [3,2,4]。在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。示例3:
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2 输出:null 输入解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。由于这两个鍊表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。 解释:这两个链表不相交,因此返回 null。注意:
- 如果两个鍊表没有交点,返回 null.
- 在返回结果后,两个鍊表仍须保持原有的结构。
- 可假定整个鍊表结构中没有循环。
- 程序尽量满足 O(n) 时间复杂度,且仅用 O(1) 内存。
记录访问历史法
先遍历其中一个链表,并把访问过的节点都记录到一个集合中。然后,再遍历另一个链表。遍历第二个链表时,每个节点都要检查是否已在第一个链表中被访问过(已被记录到集合中)。第二个链表中遇到的第一个在第一个链表中已被访问的节点就是两个链表的交会点。
代码
package io.github.rscai.leetcode.bytedance.linktree;
/**
* Merge sort
*/
public class Solution1040A {
public ListNode sortList(ListNode head) {
int length = 0;
ListNode current = head;
while (current != null) {
length++;
current = current.next;
}
return mergeSort(head, length);
}
private ListNode mergeSort(ListNode head, int length) {
if (length == 0) {
return head;
}
if (length == 1) {
return head;
}
Object[] headLengths = binarySplit(head, length);
ListNode firstHead = (ListNode) headLengths[0];
int firstLength = (Integer) headLengths[1];
ListNode secondHead = (ListNode) headLengths[2];
int secondLength = (Integer) headLengths[3];
ListNode sortedFirst = mergeSort(firstHead, firstLength);
ListNode sortedSecond = mergeSort(secondHead, secondLength);
return merge(sortedFirst, sortedSecond);
}
private Object[] binarySplit(ListNode head, int length) {
int firstLength = Math.round(length / 2.0F);
int secondLength = length - firstLength;
ListNode secondHead = head;
ListNode firstTail = head;
for (int i = 0; i < firstLength; i++) {
firstTail = secondHead;
secondHead = secondHead.next;
}
firstTail.next = null;
return new Object[]{head, firstLength, secondHead, secondLength};
}
private ListNode merge(ListNode firstHead, ListNode secondHead) {
ListNode mergedHead = null;
ListNode mergedTail = null;
ListNode firstCurrent = firstHead;
ListNode secondCurrent = secondHead;
while (firstCurrent != null || secondCurrent != null) {
if (firstCurrent == null) {
ListNode secondNext = secondCurrent.next;
secondCurrent.next = null;
ListNode[] headAndTail = append(mergedHead, mergedTail, secondCurrent);
mergedHead = headAndTail[0];
mergedTail = headAndTail[1];
secondCurrent = secondNext;
} else if (secondCurrent == null) {
ListNode firstNext = firstCurrent.next;
firstCurrent.next = null;
ListNode[] headAndTail = append(mergedHead, mergedTail, firstCurrent);
mergedHead = headAndTail[0];
mergedTail = headAndTail[1];
firstCurrent = firstNext;
} else if (firstCurrent.val < secondCurrent.val) {
ListNode firstNext = firstCurrent.next;
firstCurrent.next = null;
ListNode[] headAndTail = append(mergedHead, mergedTail, firstCurrent);
mergedHead = headAndTail[0];
mergedTail = headAndTail[1];
firstCurrent = firstNext;
} else {
ListNode secondNext = secondCurrent.next;
secondCurrent.next = null;
ListNode[] headAndTail = append(mergedHead, mergedTail, secondCurrent);
mergedHead = headAndTail[0];
mergedTail = headAndTail[1];
secondCurrent = secondNext;
}
}
return mergedHead;
}
private ListNode[] append(ListNode head, ListNode tail, ListNode node) {
if (tail == null) {
head = node;
tail = head;
} else {
tail.next = node;
tail = node;
}
return new ListNode[]{head, tail};
}
}
复杂度分析
时间复杂度
其分别遍历了两个链表各一次,时间复杂度为。
空间复杂度
其记录了其中一个链表所有节点的访问纪录。空间复杂度为。
指针偏移法
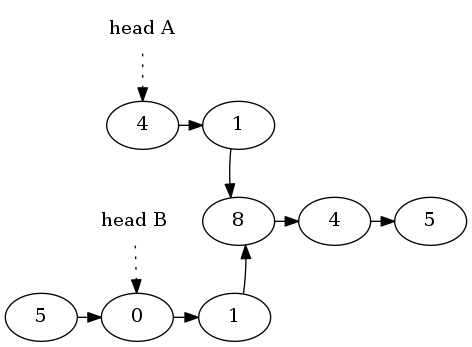
从链表尾部开始计算,相交点在两个链表中的位置是相同的。从链表头开始计算位置,则当两个链表长度相等时,相交点在两个链表中的位置也是相同的。
对于不相同的两个相交链表,如果较长的一方将头指针向后偏移两链表长度差值,则就转换成了两个长度相等且相交的链表了。
举个例子,给定如下相交链表。A链表长度5,B链表长度6。如果将B链表的头指针向后移到1(两链表长度差值为1),则转换成两个长度相等且相交的链表。
然后,再逐位比较两个链表中的节点。第一个相等的节点即为相交点。
代码
package io.github.rscai.leetcode.bytedance.linktree;
/**
* Quick sort
*/
public class Solution1040B {
public ListNode sortList(ListNode head) {
return quickSort(head);
}
private ListNode quickSort(ListNode head) {
if (head == null) {
return head;
}
if (head.next == null) {
return head;
}
ListNode[] lists = divide(head);
ListNode first = lists[0];
ListNode pivot = lists[1];
ListNode second = lists[2];
ListNode sortedFirst = quickSort(first);
ListNode sortedSecond = quickSort(second);
ListNode sortedHead = sortedFirst;
ListNode sortedTail = sortedHead;
while (sortedTail != null && sortedTail.next != null) {
sortedTail = sortedTail.next;
}
if (sortedTail != null) {
sortedTail.next = pivot;
} else {
sortedHead = pivot;
sortedTail = pivot;
}
pivot.next = sortedSecond;
return sortedHead;
}
private ListNode[] divide(ListNode head) {
ListNode pivot = head;
ListNode firstHead = null;
ListNode firstTail = firstHead;
ListNode secondHead = null;
ListNode secondTail = secondHead;
ListNode current = head.next;
pivot.next = null;
while (current != null) {
ListNode next = current.next;
current.next = null;
if (current.val < pivot.val) {
if (firstTail == null) {
firstTail = current;
firstHead = firstTail;
} else {
firstTail.next = current;
firstTail = firstTail.next;
}
} else {
if (secondTail == null) {
secondTail = current;
secondHead = secondTail;
} else {
secondTail.next = current;
secondTail = secondTail.next;
}
}
current = next;
}
return new ListNode[]{firstHead, pivot, secondHead};
}
}
首先,分别求出两个链表的长度。
然后,将较长的一个链表的头指针向后移动长度差值。
再然后,比较两个链表相同位置上的节点。第一个相同的节点即为所求相会点。
复杂度分析
时间复杂度
length遍历一遍链表以求出长度,其时间复杂度为。然后,再依序再遍历一次两个链表(最坏情况,相会在尾端)。整体时间复杂度为。
空间复杂度
使用了四个变量lengthA, lengthB, currentA和currentB。空间复杂度为。