UTF-8 编码验证

题目

UTF-8 中的一个字符可能的长度为 1 到 4 字节，遵循以下的规则：

1. 对于 1 字节的字符，字节的第一位设为0，后面7位为这个符号的unicode码。
2. 对于 n 字节的字符 (n > 1)，第一个字节的前 n 位都设为1，第 n+1 位设为0，后面字节的前两位一律设为10。剩下的没有提及的二进制位，全部为这个符号的unicode码。

这是 UTF-8 编码的工作方式：

  Char. number range  |        UTF-8 octet sequence
     (hexadecimal)    |              (binary)
  --------------------+---------------------------------------------
  0000 0000-0000 007F | 0xxxxxxx
  0000 0080-0000 07FF | 110xxxxx 10xxxxxx
  0000 0800-0000 FFFF | 1110xxxx 10xxxxxx 10xxxxxx
  0001 0000-0010 FFFF | 11110xxx 10xxxxxx 10xxxxxx 10xxxxxx

给定一个表示数据的整数数组，返回它是否为有效的 utf-8 编码。

注意:

输入是整数数组。只有每个整数的最低 8 个有效位用来存储数据。这意味着每个整数只表示 1 字节的数据。

示例 1:

data = [197, 130, 1], 表示 8 位的序列: 11000101 10000010 00000001.

返回 true 。
这是有效的 utf-8 编码，为一个2字节字符，跟着一个1字节字符。

示例 2:

data = [235, 140, 4], 表示 8 位的序列: 11101011 10001100 00000100.

返回 false 。
前 3 位都是 1 ，第 4 位为 0 表示它是一个3字节字符。
下一个字节是开头为 10 的延续字节，这是正确的。
但第二个延续字节不以 10 开头，所以是不符合规则的。

确定有限状态机法

确定有限状态机是解决正则语言、编码检验解柝的一个很有利的数学模型。

确定有限状态自动机

在计算理论中，确定有限状态自动机或确定有限自动机（英语：deterministic finite automaton, DFA）是一个能实现状态转移的自动机。对于一个给定的属于该自动机的状态和一个属于该自动机字母表 $\Sigma$ 的字元，它都能根据事先给定的转移函式转移到下一个状态（这个状态可以是先前那个状态）。

基础概念

定义

确定有限状态自动机 ${\mathcal {A}}$ 是由

• 一个非空有限的状态集合 $Q$
• 一个输入字母表 $\Sigma$ （非空有限的字元集合）
• 一个转移函式 $\delta :Q\times \Sigma \rightarrow Q$（例如： $\delta \left(q,\sigma \right)=p,\left(p,q\in Q,\sigma \in \Sigma \right)$）
• 一个开始状态 $s\in Q$
• 一个接受状态的集合 $F\subseteq Q$

所组成的5-元组。因此一个DFA可以写成这样的形式： ${\mathcal {A}}=\left(Q,\Sigma ,\delta ,s,F\right)$。

工作方式（非正式的语意)

确定有限状态自动机从起始状态开始，一个字元接一个字元地读入一个字串 $w\in \Sigma ^{*}$（这里的 ${}^{*}$指示Kleene星号算子。），并根据给定的转移函式一步一步地转移至下一个状态。在读完该字串后，如果该自动机停在一个属于F的接受状态，那么它就接受该字串，反之则拒绝该字串。

扩充转移函式

为了在保证严谨的前提下，方便地叙述关于DFA的内容，我们定义如下扩充的转移函式：$\delta ^{*}:Q\times \Sigma ^{*}\rightarrow Q$。

• 其中$\delta ^{*}\left(q,w\right)$是自动机从状态q顺序读入字串w后达到的状态
• 扩充转移函式递回的定义为：
  • $\delta ^{*}\left(q,\epsilon \right)=q$
  • $\delta ^{*}\left(q,u\sigma \right)=\delta (\delta ^{*}(q,u),\sigma ),\forall u\in \Sigma ^{*},\sigma \in \Sigma$

工作方式（正式的语意）

对于一个确定有限状态自动机 ${\mathcal {A}}=\left(Q,\Sigma ,\delta ,s,F\right)$，如果 $\delta ^{*}\left(s,w\right)\in F$，我们就说该自动机接受字串w，反之则表明该自动机拒绝字串w。

被一个确定有限自动机接受的语言（或者叫「被辨识的语言」）定义为： ${\mathcal {L}}({\mathcal {A}})=\{w\in \Sigma ^{*}|{\mathcal {A}}~接受字串 ~w\}，$也就是由所有被接受的字串组成的集合。

参考

• 确定有限状态自动机

针对本题，定义：

• 一个非空有限的状态集合{start, twoByteFirst, threeByteFirst, threeByteSecond, fourByteFirst, fourByteSecond, fourByteThird}
• 一个轮入字母表{0xxxxxxx, 110xxxxx, 1110xxxx, 11110xxx, 10xxxxxx}
• 一个转移函数

• 一个开始状态 start
• 一个接受状态的集合 {start}

举个例子，轮入整数序列[197, 130, 1], 表示 8 位的序列: 11000101 10000010 00000001。

• state初始为start；
• 输入第一个8位值11000101，其符合110xxxxx，所以转移状态至twoByteFirst
• 输入第二个8位值10000010，其符合10xxxxxx，所以转移状态至start
• 输入第三个8位值00000001，其符合0xxxxxxx，所以保持状态为start

最终状态停留在start，属于接受状态集合，所以该整数序列是有效的UTF-8编码。

代码实现

将所有状态值都定义为常量，

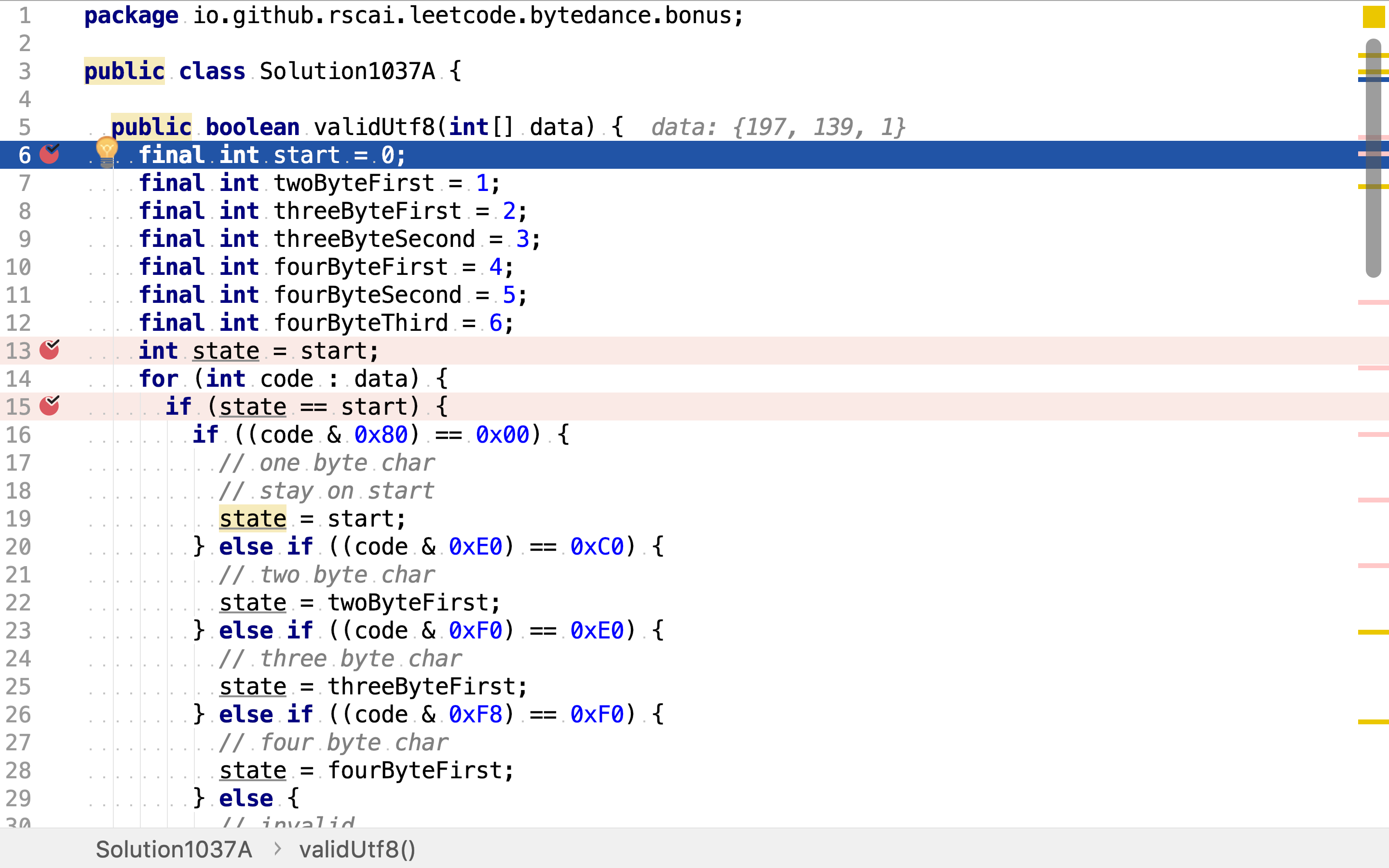
状态初始化为start，

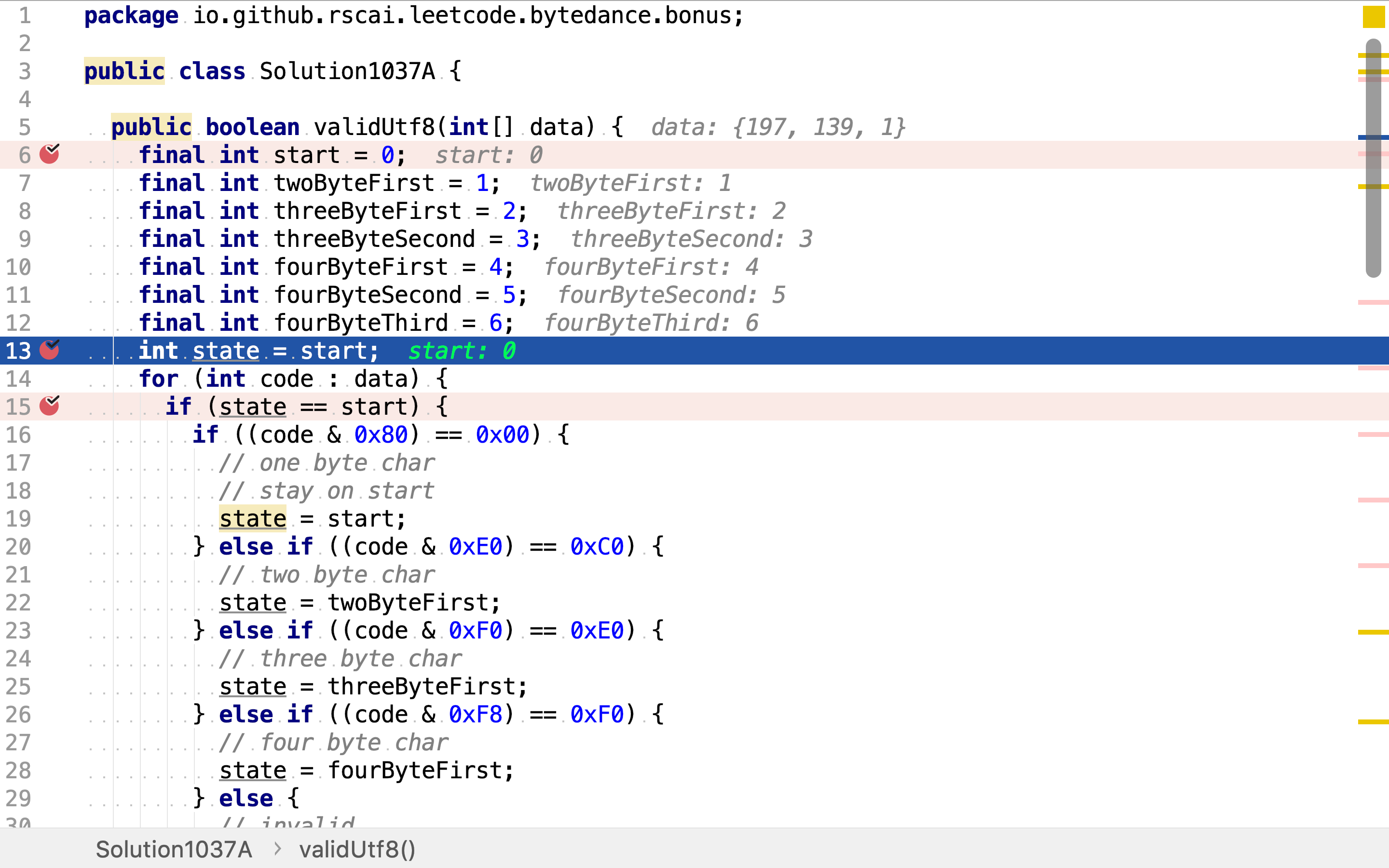
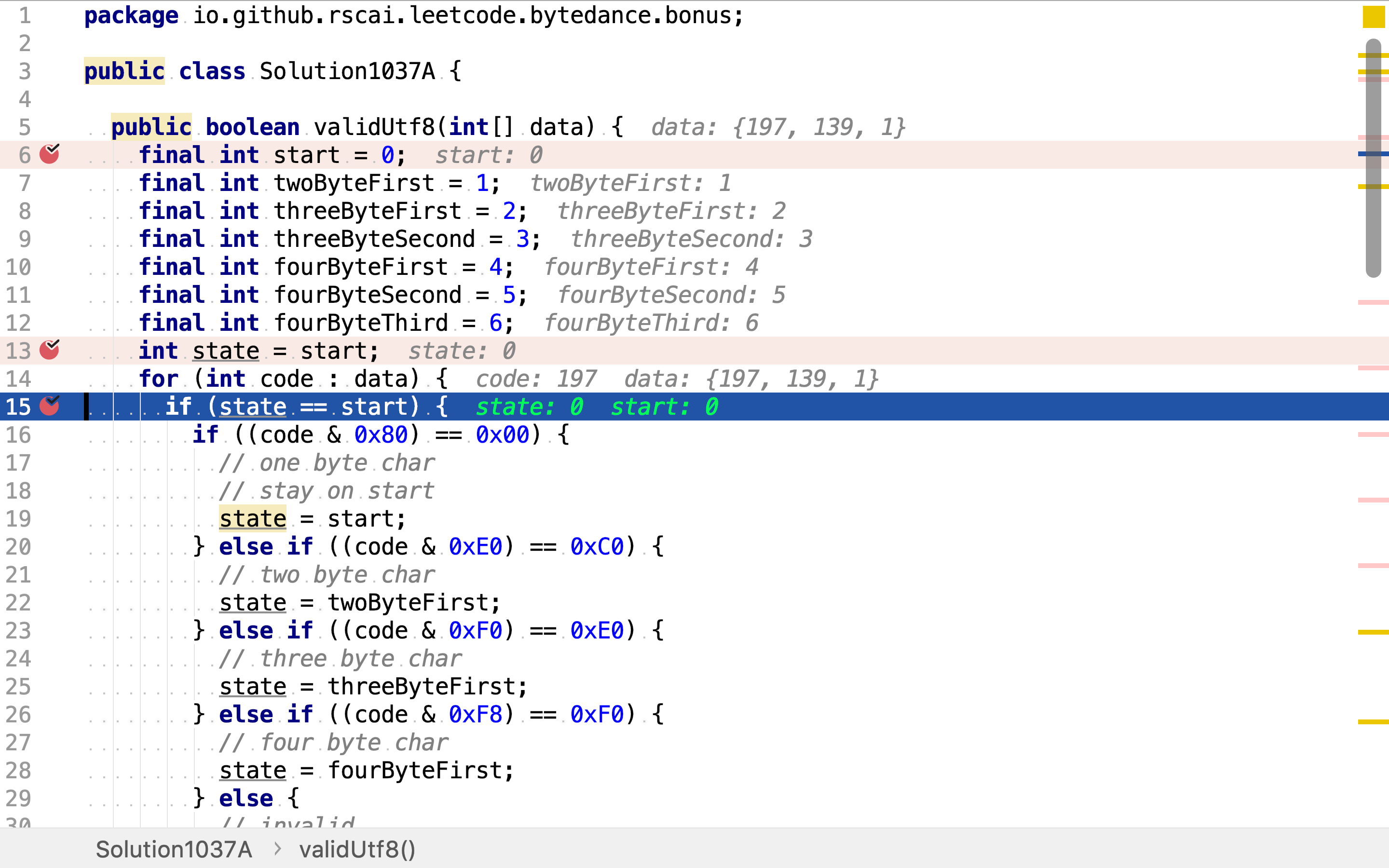
使用for循环逐一输入整数，驱动「确定有限状态机」

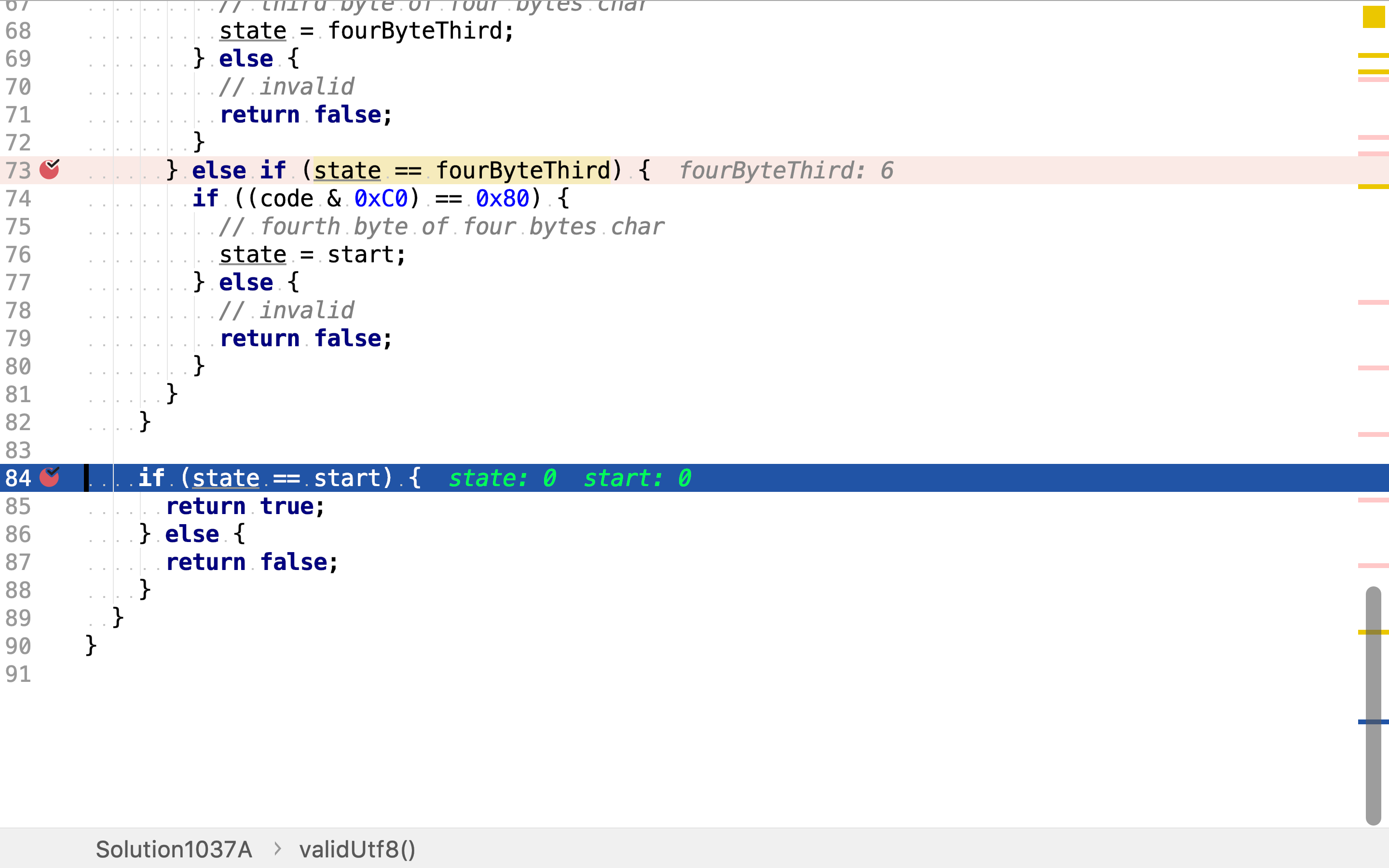
最后，判断状态是否为可接受状态。

复杂度分析

时间复杂度

本演算法只遍历了一遍整数序列，所以时间复杂度为$\mathcal{O}(n)$。

空间复杂度

使用了一个变量state，所以空间复杂度为$\mathcal{O}(1)$。