最长连续序列

题目

给定一个未排序的整数数组，找出最长连续序列的长度。

要求算法的时间复杂度为 O(n)。

示例:

输入: [100, 4, 200, 1, 3, 2]
输出: 4
解释: 最长连续序列是 [1, 2, 3, 4]。它的长度为 4。

快速排序法

先使用「快速排序」将无序数组转换为有序递增数组，再一次遍历找出最长连续序列。

快速排序

快速排序（英语：Quicksort），又称划分交换排序（partition-exchange sort），简称快排，一种排序演算法，最早由东尼·霍尔提出。在平均状况下，排序$n$个项目要${\displaystyle \ O(n\log n)}$（大O符号）次比较。在最坏状况下则需要${\displaystyle O(n^{2})}$次比较，但这种状况并不常见。事实上，快速排序${\displaystyle \Theta (n\log n)}$通常明显比其他演算法更快，因为它的内部回圈（inner loop）可以在大部分的架构上很有效率地达成。

代码

Arrays.sort实现了Dual-Pivot快速排序。

    /*
     * Sorting methods. Note that all public "sort" methods take the
     * same form: Performing argument checks if necessary, and then
     * expanding arguments into those required for the internal
     * implementation methods residing in other package-private
     * classes (except for legacyMergeSort, included in this class).
     */

    /**
     * Sorts the specified array into ascending numerical order.
     *
     * <p>Implementation note: The sorting algorithm is a Dual-Pivot Quicksort
     * by Vladimir Yaroslavskiy, Jon Bentley, and Joshua Bloch. This algorithm
     * offers O(n log(n)) performance on many data sets that cause other
     * quicksorts to degrade to quadratic performance, and is typically
     * faster than traditional (one-pivot) Quicksort implementations.
     *
     * @param a the array to be sorted
     */
    public static void sort(int[] a) {
        DualPivotQuicksort.sort(a, 0, a.length - 1, null, 0, 0);
    }

复杂度分析

时间复杂度

Arrays.sort实现的Dual-Pivot快速排序时间复杂度为$\mathcal{O}(n \log{n})$，一次遍历数组时间复杂度为$\mathcal{O}(n)$。总体时间复杂度为：

$$\begin{aligned} C_{time} &= \mathcal{O}(n \log{n}) + \mathcal{O}(n) \\ &= \mathcal{O}(n \log{n}) \end{aligned}$$

空间复杂度

Arrays.sort创建一个临时数组用于排序。所以空间复杂度为$\mathcal{O}(n)$。

        // Use or create temporary array b for merging
        int[] b;                 // temp array; alternates with a
        int ao, bo;              // array offsets from 'left'
        int blen = right - left; // space needed for b
        if (work == null || workLen < blen || workBase + blen > work.length) {
            work = new int[blen];
            workBase = 0;
        }
        if (odd == 0) {
            System.arraycopy(a, left, work, workBase, blen);
            b = a;
            bo = 0;
            a = work;
            ao = workBase - left;
        } else {
            b = work;
            ao = 0;
            bo = workBase - left;
        }

动态规划法

动态规划

动态规划（英语：Dynamic programming，简称DP）是一种在数学、管理科学、电脑科学、经济学和生物资讯学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。

动态规划常常适用于有重叠子问题和最佳子结构性质的问题，动态规划方法所耗时间往往远少于朴素解法。

动态规划背后的基本思想非常简单。大致上，若要解一个给定问题，我们需要解其不同部分（即子问题），再根据子问题的解以得出原问题的解。

通常许多子问题非常相似，为此动态规划法试图仅仅解决每个子问题一次，从而减少计算量：一旦某个给定子问题的解已经算出，则将其记忆化储存，以便下次需要同一个子问题解之时直接查表。这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。

概述

动态规划在寻找有很多重叠子问题的情况的最佳解时有效。它将问题重新组合成子问题。为了避免多次解决这些子问题，它们的结果都逐渐被计算并被储存，从简单的问题直到整个问题都被解决。因此，动态规划储存递回时的结果，因而不会在解决同样的问题时花费时间。

动态规划只能应用于有最佳子结构的问题。最佳子结构的意思是局部最佳解能决定全域最佳解（对有些问题这个要求并不能完全满足，故有时需要引入一定的近似）。简单地说，问题能够分解成子问题来解决。

适用情况

1. 最佳子结构性质。如果问题的最佳解所包含的子问题的解也是最佳的，我们就称该问题具有最佳子结构性质（即满足最佳化原理）。最佳子结构性质为动态规划演算法解决问题提供了重要线索。
2. 无后效性。即子问题的解一旦确定，就不再改变，不受在这之后、包含它的更大的问题的求解决策影响。
3. 子问题重叠性质。子问题重叠性质是指在用递回演算法自顶向下对问题进行求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。动态规划演算法正是利用了这种子问题的重叠性质，对每一个子问题只计算一次，然后将其计算结果储存在一个表格中，当再次需要计算已经计算过的子问题时，只是在表格中简单地检视一下结果，从而获得较高的效率。

参考

• 动态规划
• Dynamic Programming

一个整数所处于的连续子序列等于以其前继值为边的连续序列加其自身再加以甚后继值为边缘点的连续序列。递推公式为：

$$f(n) = f(n-1) + 1 + f(n+1)$$

举个例子，给定数组[100, 4, 200, 1, 3, 2]。100所处的连续序列长度等于以99为右边端点的连续序列长度加100自身长度1再加以101为左边端点的连续序列长度。依此类推，4所处的连续序列长度等于以3为右边端点连续序列长度加自身长度1再加以5为左边端点的连续序列长度。

将子问题之间的关系以树的形式展现，可以发现有很多子树是重复的，即这些子问题的解被依赖多次。存储些子问题的解可以避免重复计算。

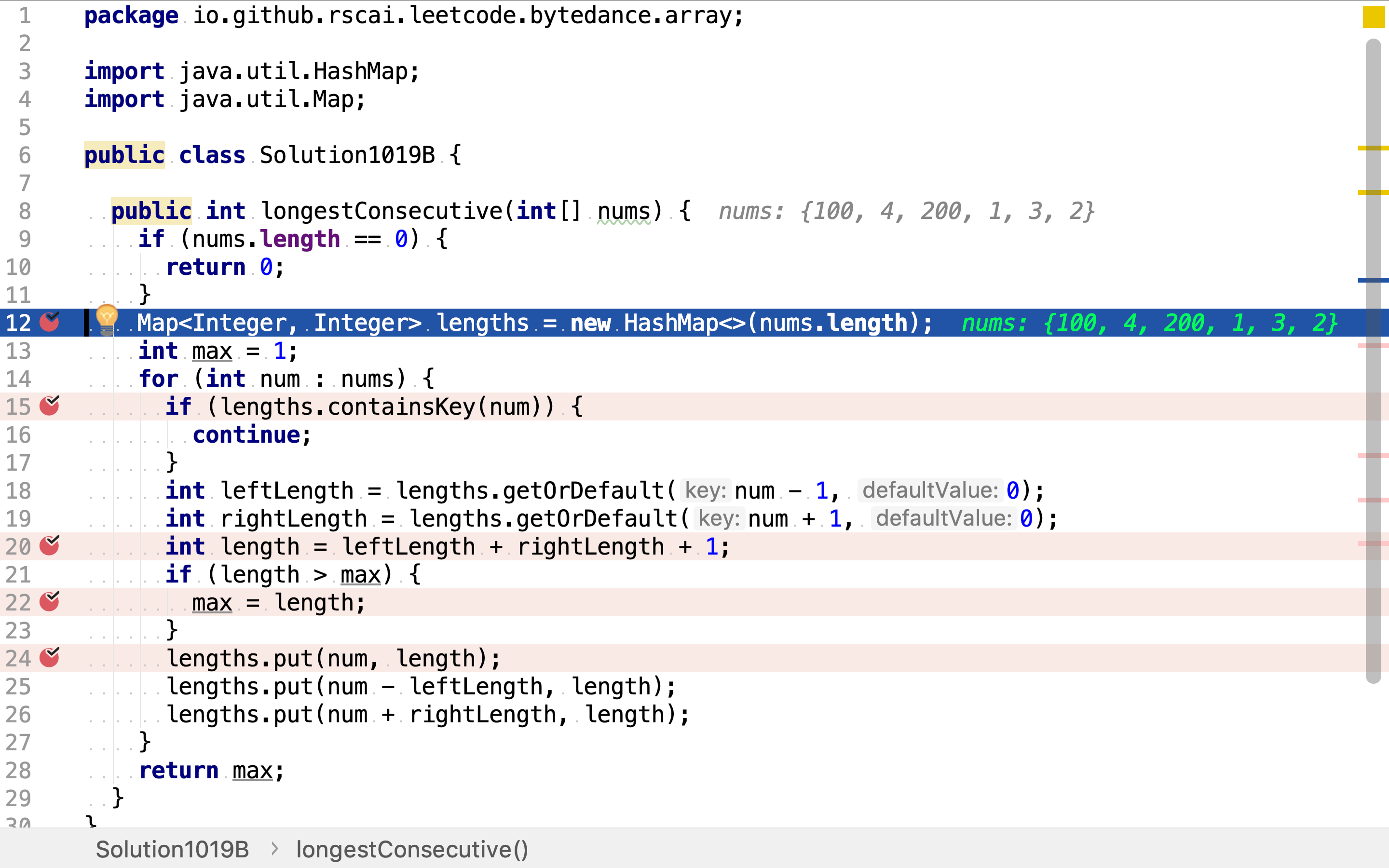
代码

首先，创建一个HashMap用以存储子问题的解。

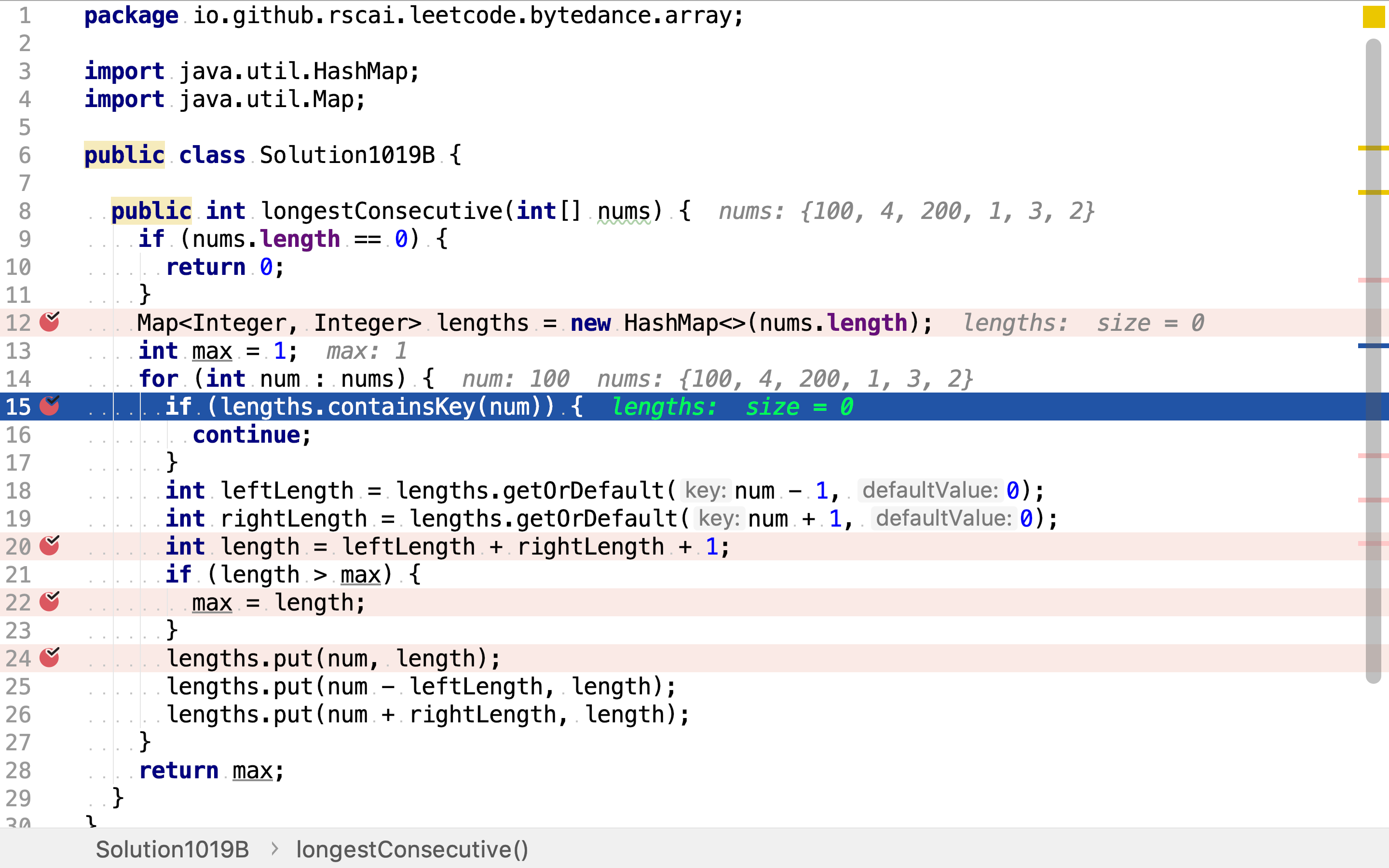
然后，遍历数组，逐一计算子问题--包含某个元素的最长连续序列长度及边缘端点。若该子问题已被计算过（HashMap中已包含该问题的解）则略过；

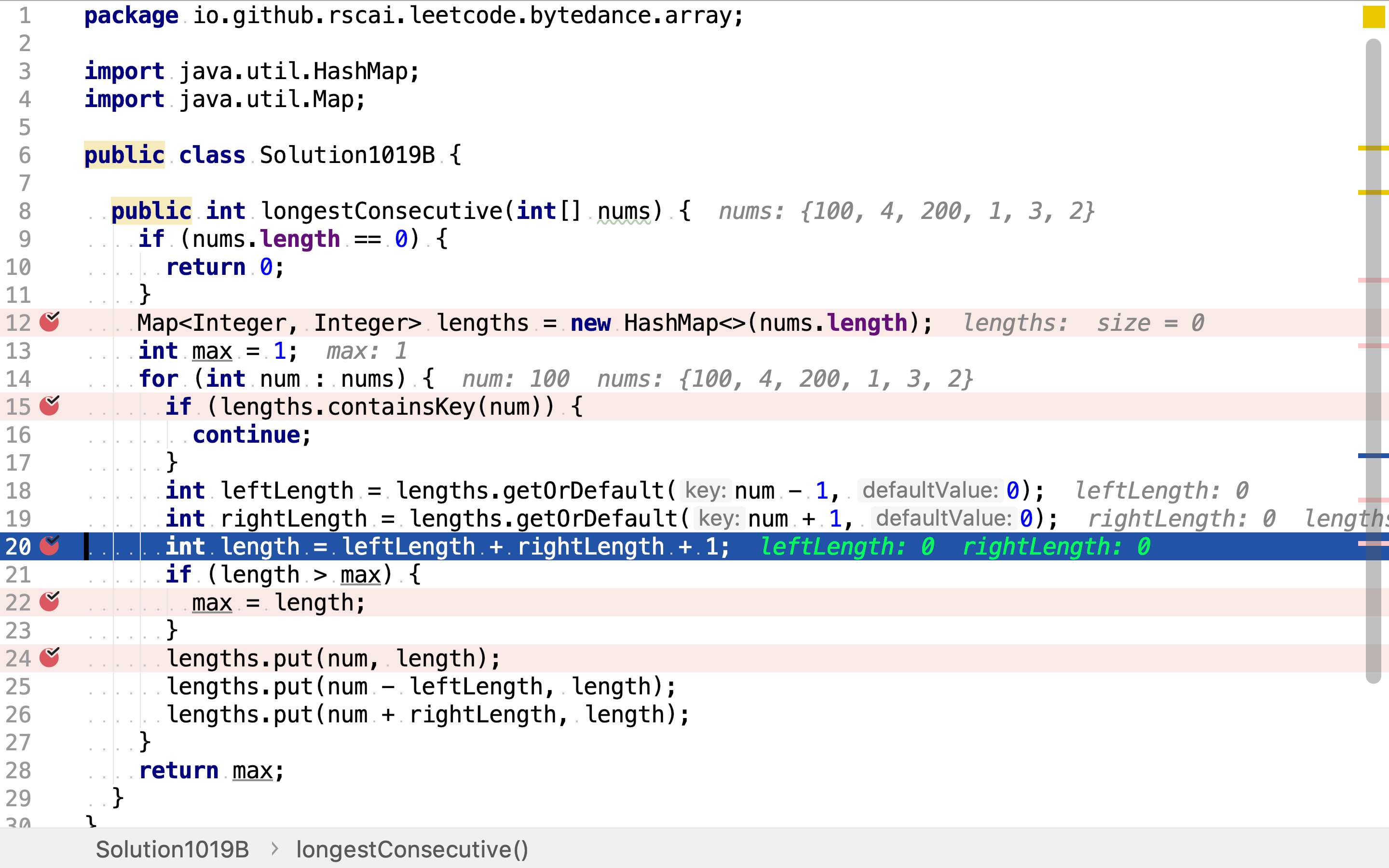
否则，计算该子问题。计算方法为：以其前继为边缘端点的连续序列长度加上以其后继为边缘端点的连续序列长度再加上自身长度1。

将子问题解存储起来。同时得到了该点所处最长连续序列的左右边缘点的解，同时也存储起来。连续序列之间存在互相包含关系，如[1, 2, 3]包含[1, 2]。

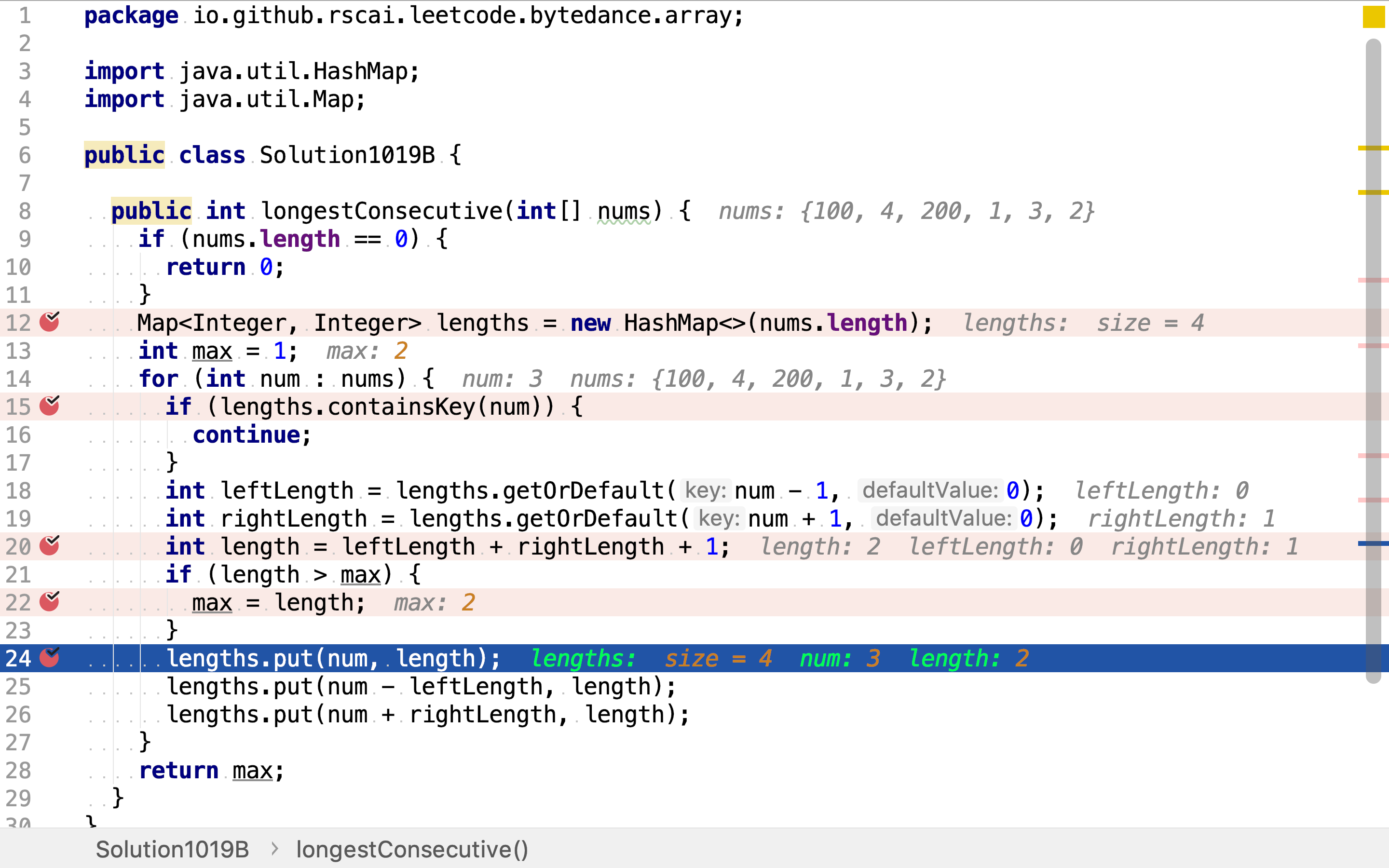
在计算子问题的同时，寻找最长连续子序列。

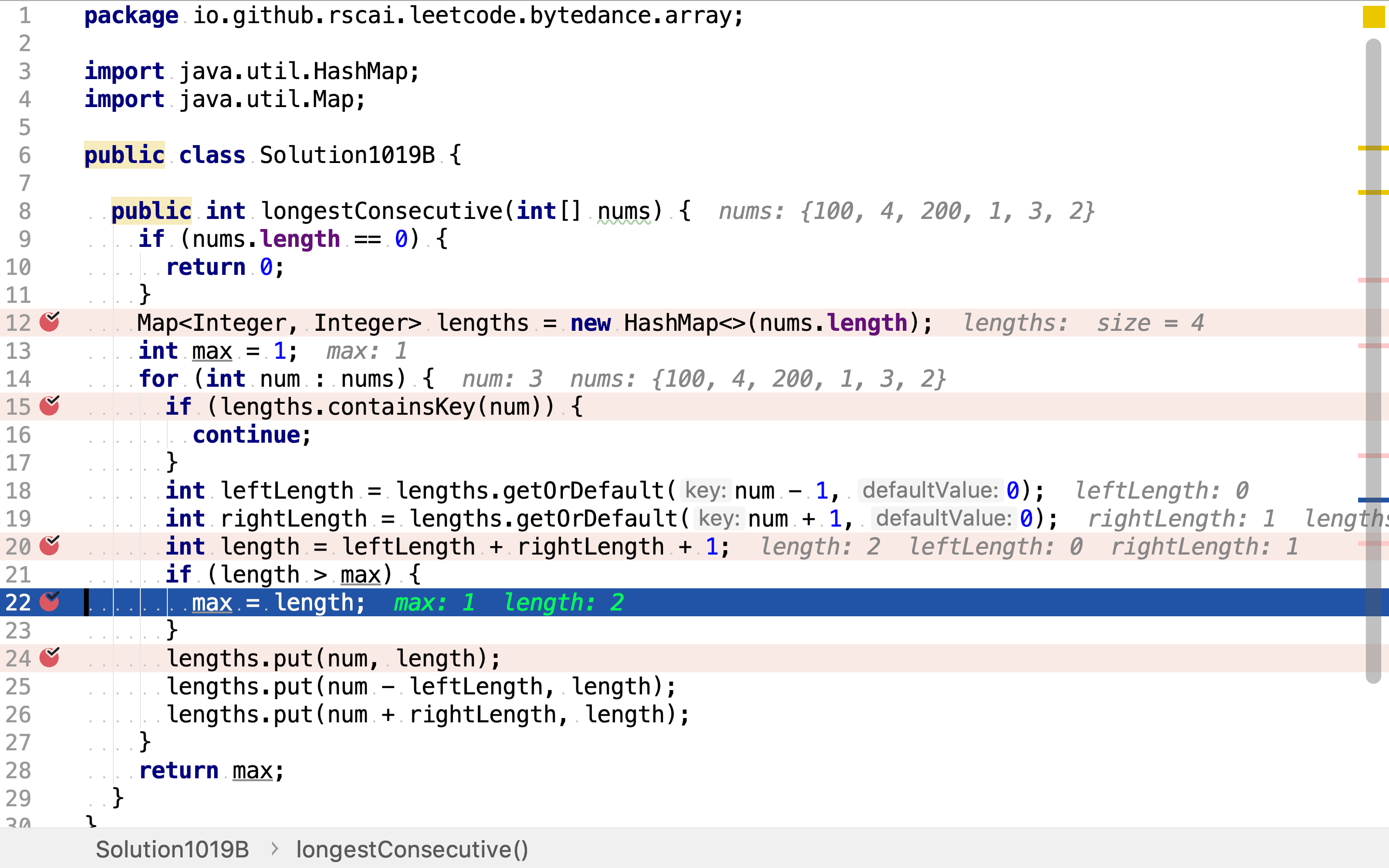
复杂度分析

时间复杂度

本演算法祇遍历了一次数组，HashMap的读写操作都是常数时间复杂度。所以：

$$\begin{aligned} C_{time} &= \mathcal{O}(n) + \mathcal{O}(1) \\ &= \mathcal{O}(n) \end{aligned}$$

空间复杂度

假设数组长度为$n$，HashMap最多保存$n$个键值对。空间复杂度为$\mathcal{O}(n)$。

参考

• 快速排序