最长公共前缀

题目

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 ""。

示例 1:
输入: ["flower","flow","flight"]
输出: "fl"
示例 2:
输入: ["dog","racecar","car"]
输出: ""
解释: 输入不存在公共前缀。
说明:

所有输入只包含小写字母 a-z 。

逐列扫描法

把字符串水平放罝并堆叠起来，得到一个行列表。

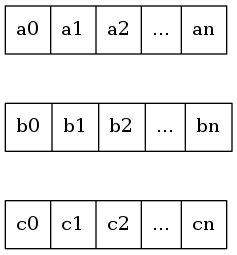
从左往右逐一扫描，当遇到值不相同列时，从头到该列前一列组成的子串即是最长公共前缀。

举个例子，给定三个字符串["flower","flow","flight"]。将字符中水平放置并堆叠起来，得到：

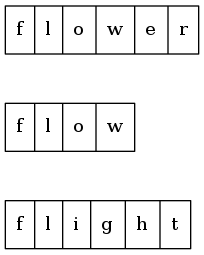
从左往右逐列扫描。第一列中，三个字符串的字符都相同。

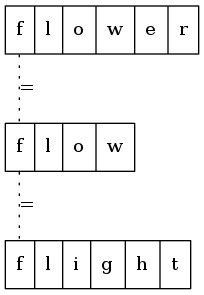
第二列中，三个字符串的字符也都相同。

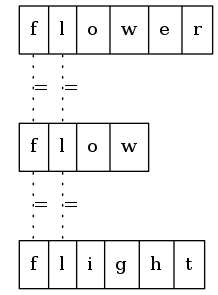
第三列中，三个字符串的字符不相同。

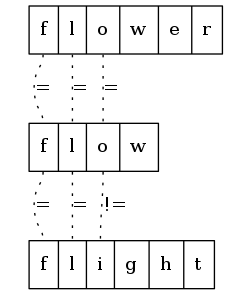
所以，最长公共前缀是从头开始至第二列的子串fl。

代码实现

package io.github.rscai.leetcode.bytedance.string; public class Solution1014A { public String longestCommonPrefix(String[] strs) { if (strs.length == 0) { return ""; } for (int i = 0; i < strs[0].length(); i++) { char ch = strs[0].charAt(i); for (String str : strs) { if (str.length() <= i || ch != str.charAt(i)) { return strs[0].substring(0, i); } } } return strs[0]; } }

如果输入的字符串数量是零，则最长公共前缀就是空串。

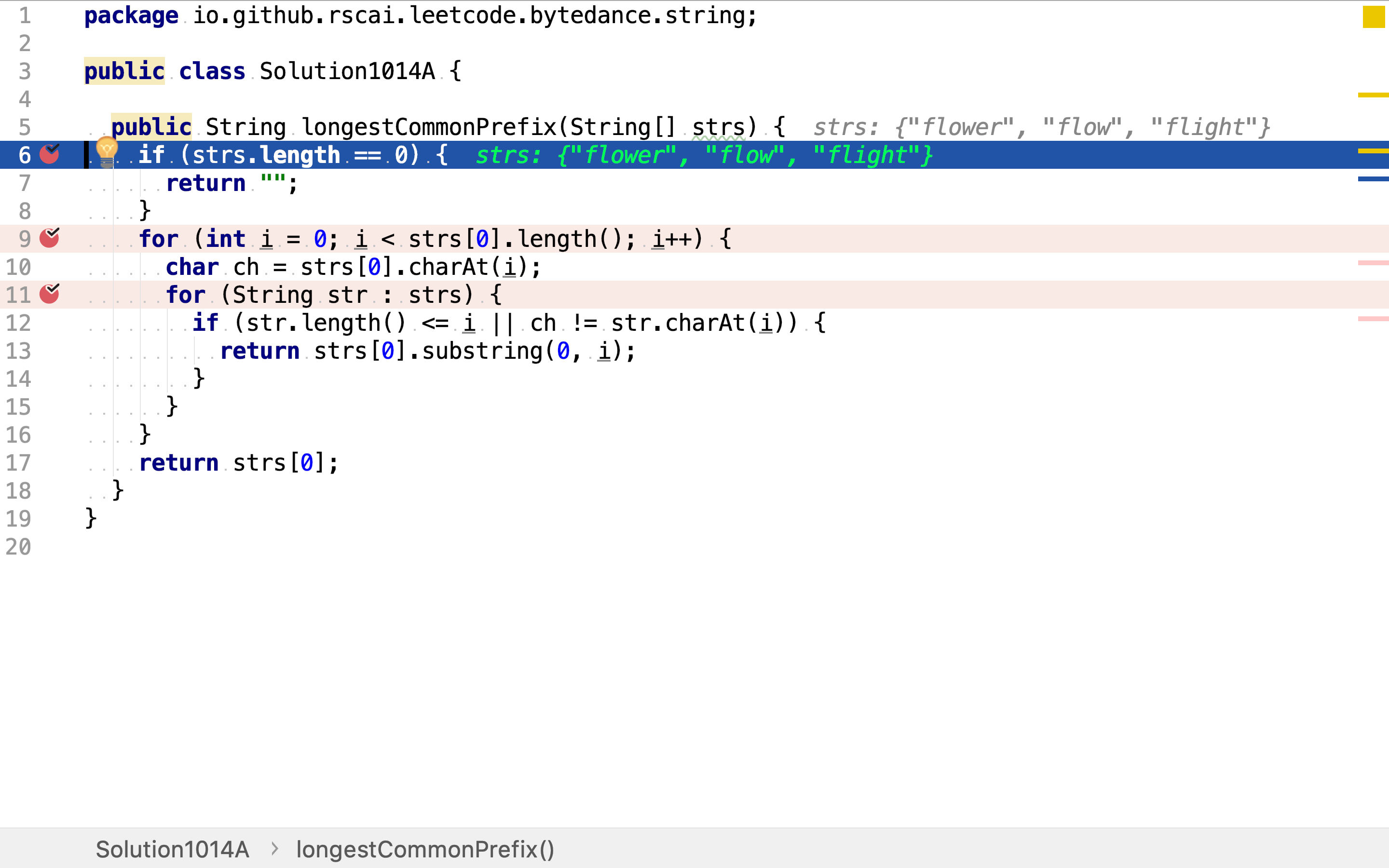
从头往后逐列扫描

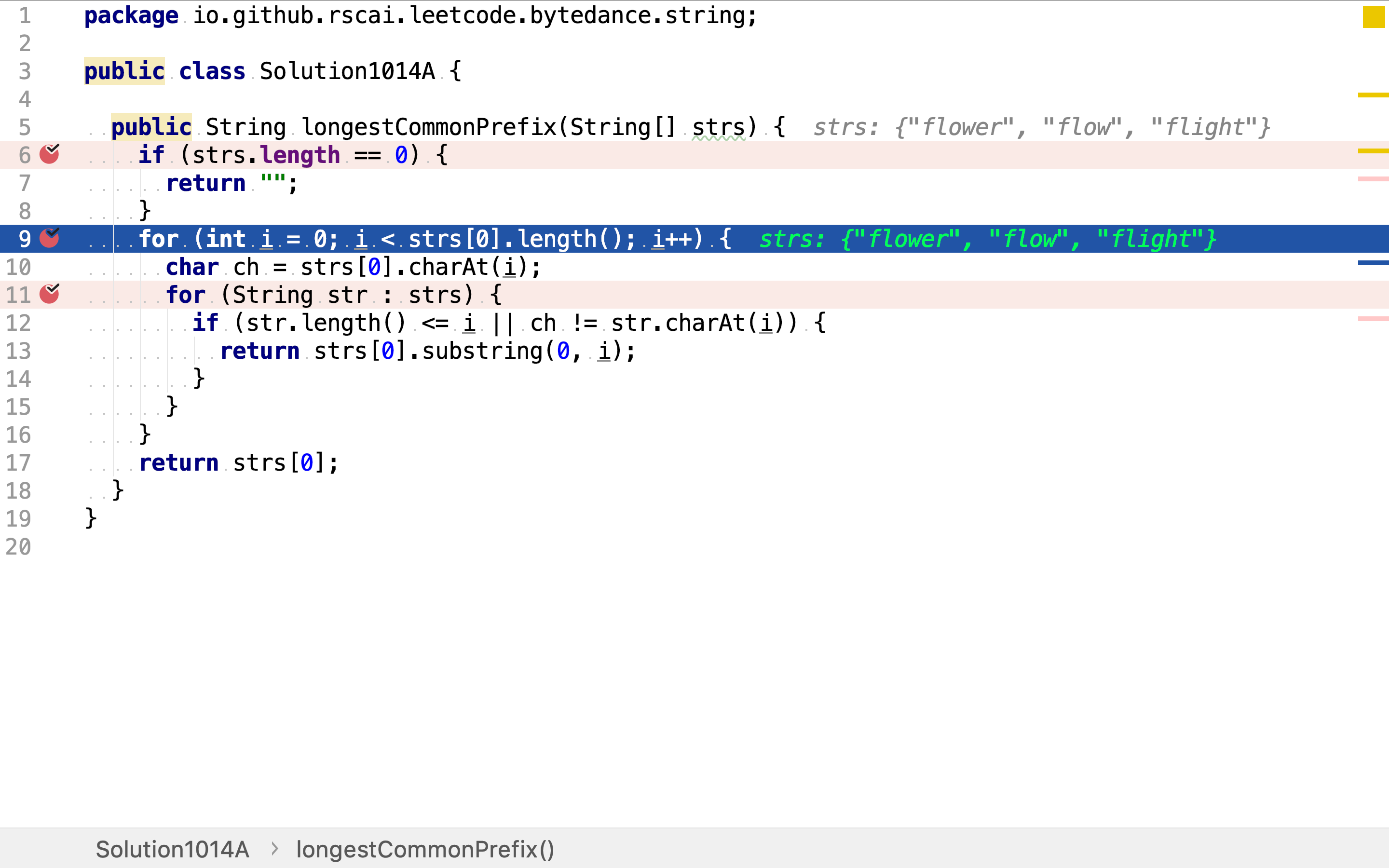
当遇到第一列字符不相同的列时，就可确定最长公共前缀了：

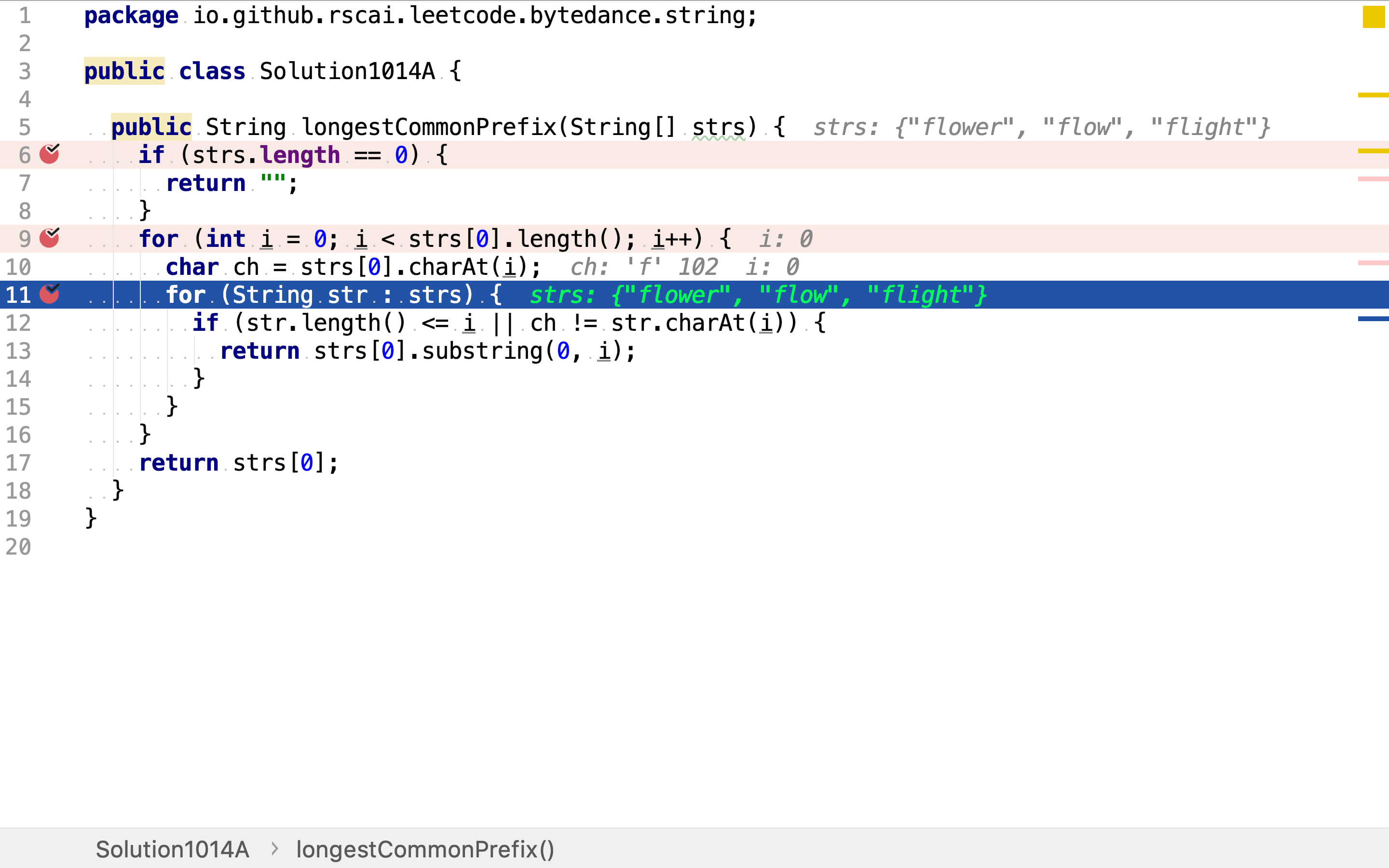
复杂度分析

时间复杂度

最坏情况下，所有字符中都是相同的，则本演算法要遍历所有字符串中的所有字符。设所有字符串中字符数量和为 $n$ ，则时间复杂度为 $\mathcal{O}(n)$ 。

空间复杂度

只使用了两个变量i, ch，所以空间复杂度为 $\mathcal{O}(1)$ 。

分治法

在电脑科学中，分治法是建基于多项分支递回的一种很重要的演算法范式。字面上的解释是「分而治之」，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合併。

这个技巧是很多高效演算法的基础，如排序演算法（快速排序、合併排序）、傅立叶变换（快速傅立叶变换）。

另一方面，理解及设计分治法演算法的能力需要一定时间去掌握。正如以归纳法去证明一个理论，为了使递回能够推行，很多时候需要用一个较为概括或复杂的问题去取代原有问题。而且并没有一个系统性的方法去适当地概括问题。

分治法这个名称有时亦会用于将问题简化为只有一个细问题的演算法，例如用于在已排序的列中寻找其中一项的折半搜寻演算法（或是在数值分析中类似的勘根演算法）。这些演算法比一般的分治演算法更能有效地执行。其中，假如演算法使用尾部递回的话，便能转换成简单的回圈。但在这广义之下，所有使用递回或回圈的演算法均被视作「分治演算法」。因此，有些作者考虑「分治法」这个名称应只用于每个有最少两个子问题的演算法。而只有一个子问题的曾被建议使用减治法这个名称。

分治演算法通常以数学归纳法来验证。而它的计算成本则多数以解递回关系式来判定。

优势

解决困难问题

分治演算法是一个解决复杂问题的好工具，它可以把问题分解成若干个子问题，把子问题逐个解决，再组合到一起形成大问题的答案。比如，汉诺塔问题如果採用分治演算法，可以把高度为n的塔的问题转换成高度为n-1的塔来解决，如此重复，直至问题化简到可以很容易的处理为止。

实现

回圈递回

在每一层递回上都有三个步骤：

分解：将原问题分解为若干个规模较小，相对独立，与原问题形式相同的子问题。

解决：若子问题规模较小且易于解决时，则直接解。否则，递回地解决各子问题。

合併：将各子问题的解合併为原问题的解。

举个例子，给定四个字符串["flower", "flow", "flexible", "flexion"]。将其不断一分为二，直至每一份只包含一个字符串。

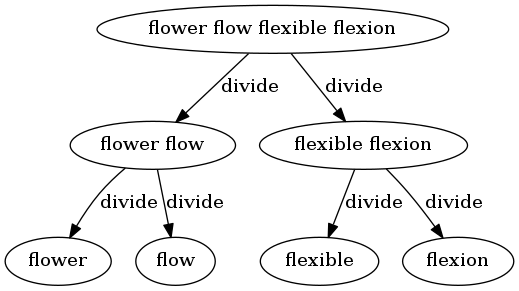
然后，分别处理「治」每一份：

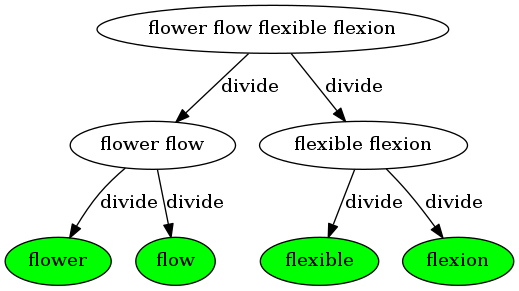
再然后，将每一小份的处理结果向上归併。「最长公共前缀」问题的归併就是取两个字符串的最长公共前缀：

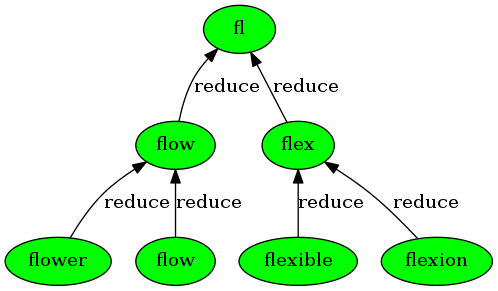
归併到最后仅剩一个结果时，该结果就是所求解。

代码实现

package io.github.rscai.leetcode.bytedance.string; public class Solution1014B { public String longestCommonPrefix(String[] strs) { if (strs.length == 0) { return ""; } return longestCommonPrefix(strs, 0, strs.length); } private String longestCommonPrefix(String[] strs, int start, int end) { if (end - start == 1) { return strs[start]; } int mid = (end + start) / 2; String firstCommonPrefix = longestCommonPrefix(strs, start, mid); String secondCommonPrefix = longestCommonPrefix(strs, mid, end); return commonPrefix(firstCommonPrefix, secondCommonPrefix); } private String commonPrefix(String first, String second) { int minLength = Math.min(first.length(), second.length()); for (int i = 0; i < minLength; i++) { if (first.charAt(i) != second.charAt(i)) { return first.substring(0, i); } } return first.substring(0, minLength); } }

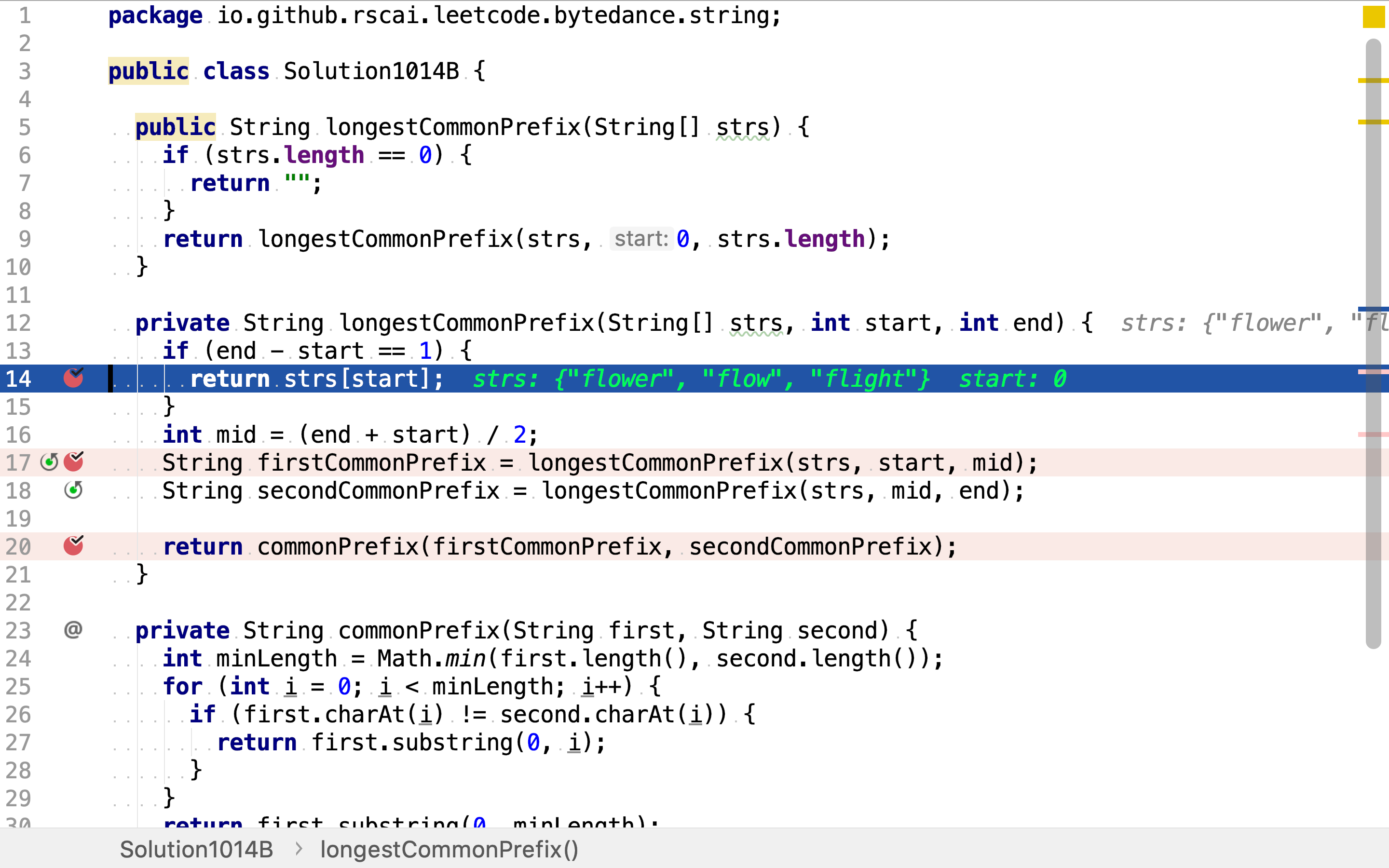
首先，使用二分法将字符串列表逐渐拆分，并计算拆分后的字符串的最长公共前缀。

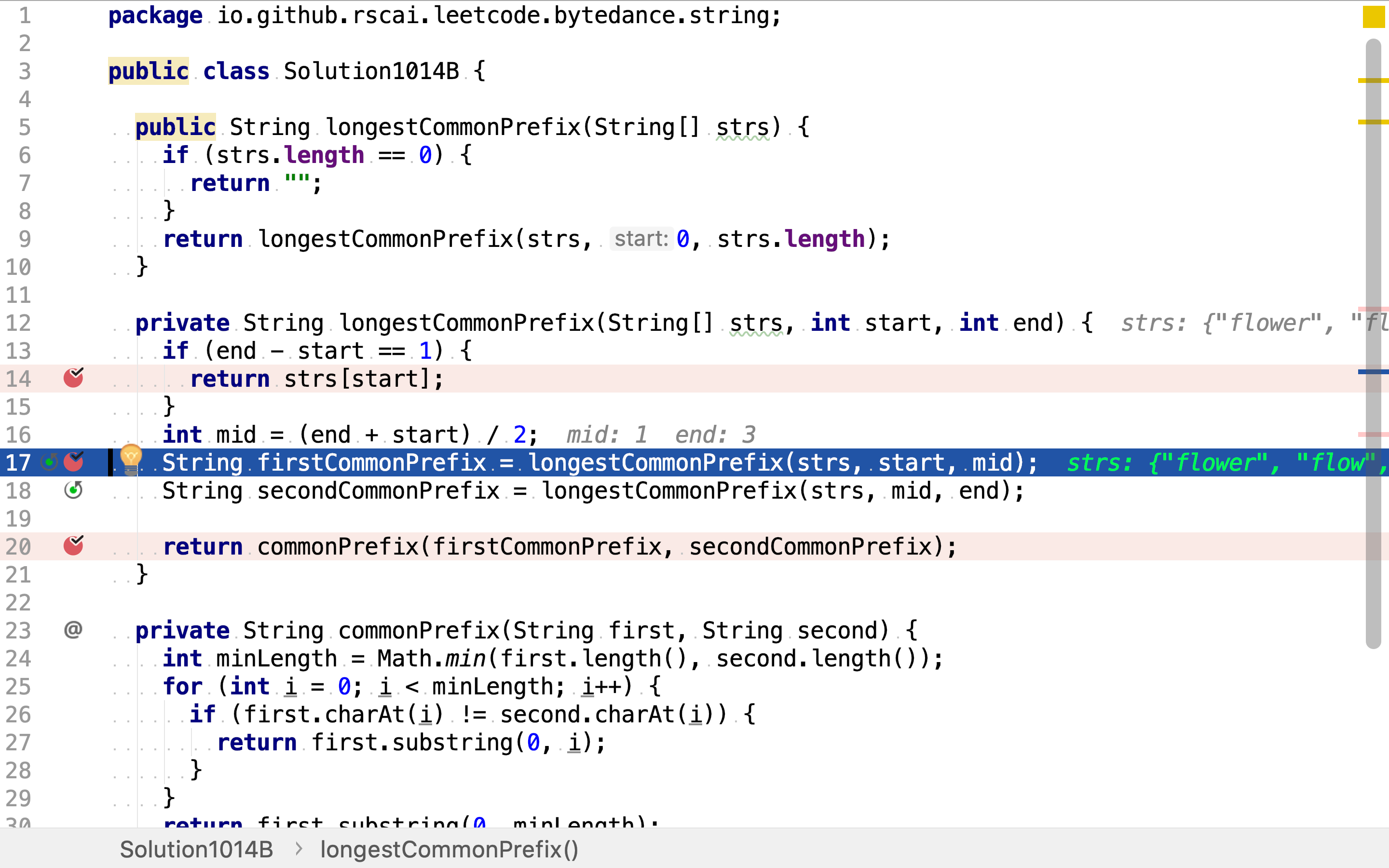
当仅剩一条字符串时，停止拆分。一条字符串的最长公共前缀即其自身。

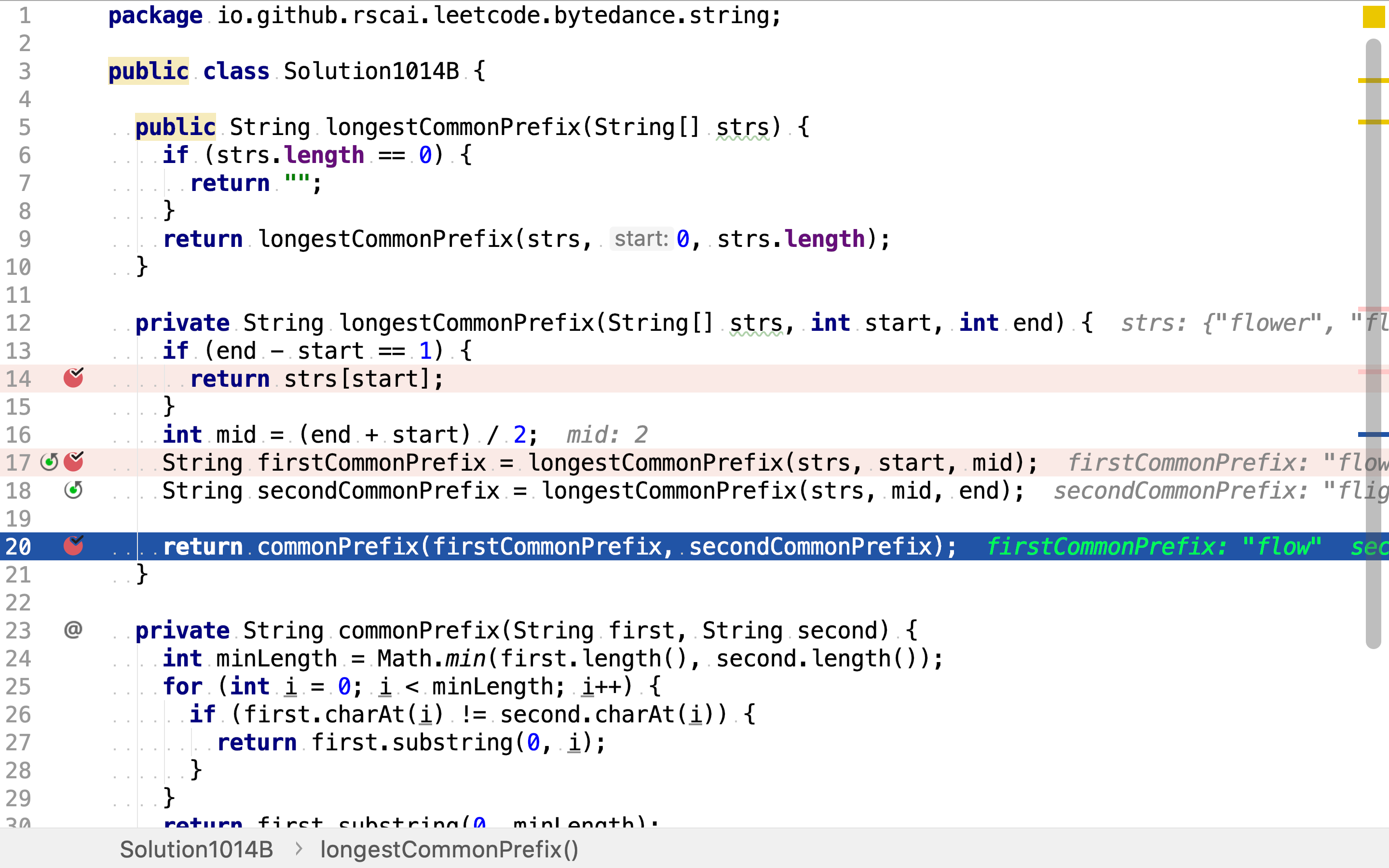
然后，归併结果。两组字符串各自最长公共前缀的最长公共前缀即所有字符串的最长公共前缀。