三数之和
题目
给定一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?找出所有满足条件且不重复的三元组。
注意:答案中不可以包含重复的三元组。
例如, 给定数组 nums = [-1, 0, 1, 2, -1, -4],
满足要求的三元组集合为:
[
[-1, 0, 1],
[-1, -1, 2]
]
穷举法
使用穷举法罗列所有三元组组合。三元组由以下步骤产生:
- 从数组中取出一个整数
- 再从上个取出的整数后面取出一个整数
- 再从上个取出的整数后面取出一个整数
**为避免产生重复的三元组,每个整数都是从三元组中上一个整数之后的剩余整数中选取。(但元素值有重复的,所以依旧会有重复的三元组,但数量大幅减少了。)
然后再选取出和为0的三元组。
举个例子,给定整数数组[-1, 0, 1, 2, -1, -4]。
- 首先,从数组中取出一个整数。有
-1, 0, 1, 2四种选择。因为是三元组且第二个和第三个整数是从第一个整数之后的整数中选取的。所以第一个整数之后的剩余整数不能少于2。
- 然后,从第一个整数之后的剩余整数中选取一个整数。若第一个整数选了第一个-1,则第二个整数有
0, 1, 2, -1四种选择;若第一个整数选了第二个0,则第二个整数有1, 2, -1三种选择;依此类推。。。
- 最后,从第二个整数之后的剩余整数中选取一个整数。若第二个整数选了第二个0,则第三个整数有
1, 2, -1, -4四种选择;若第二个整数选了第三个1,则第三个整数有2, -1, -4三种选择。

代码
package io.github.rscai.leetcode.bytedance.array;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.HashSet;
import java.util.List;
import java.util.Set;
public class Solution1020A {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> result = new ArrayList<>();
for (int i = 0; i < nums.length - 2; i++) {
for (int j = i + 1; j < nums.length - 1; j++) {
for (int k = j + 1; k < nums.length; k++) {
if (nums[i] + nums[j] + nums[k] == 0) {
result.add(Arrays.asList(nums[i], nums[j], nums[k]));
}
}
}
}
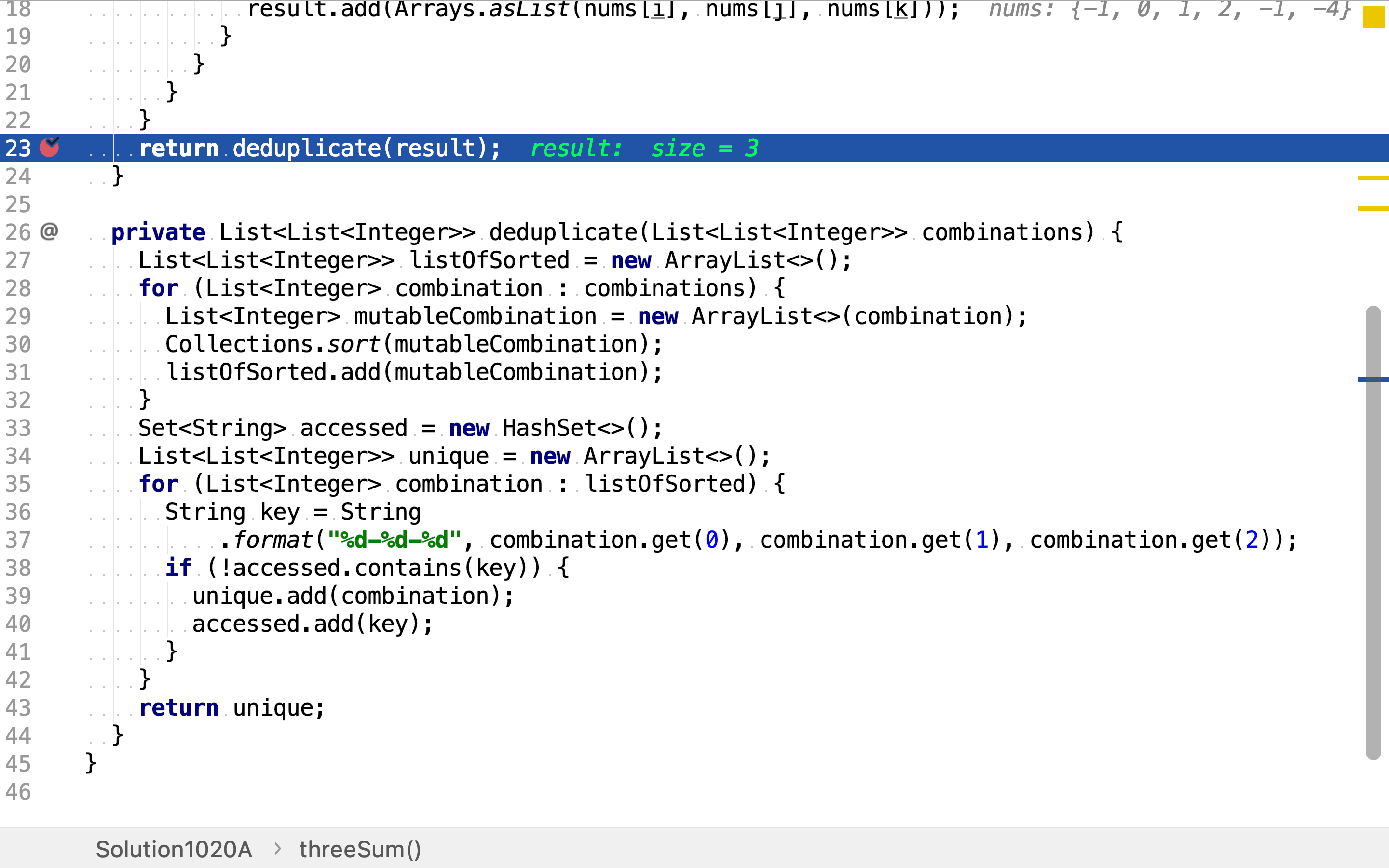
return deduplicate(result);
}
private List<List<Integer>> deduplicate(List<List<Integer>> combinations) {
List<List<Integer>> listOfSorted = new ArrayList<>();
for (List<Integer> combination : combinations) {
List<Integer> mutableCombination = new ArrayList<>(combination);
Collections.sort(mutableCombination);
listOfSorted.add(mutableCombination);
}
Set<String> accessed = new HashSet<>();
List<List<Integer>> unique = new ArrayList<>();
for (List<Integer> combination : listOfSorted) {
String key = String
.format("%d-%d-%d", combination.get(0), combination.get(1), combination.get(2));
if (!accessed.contains(key)) {
unique.add(combination);
accessed.add(key);
}
}
return unique;
}
}
首先,罗列三元组中第一个整数的所有选择。
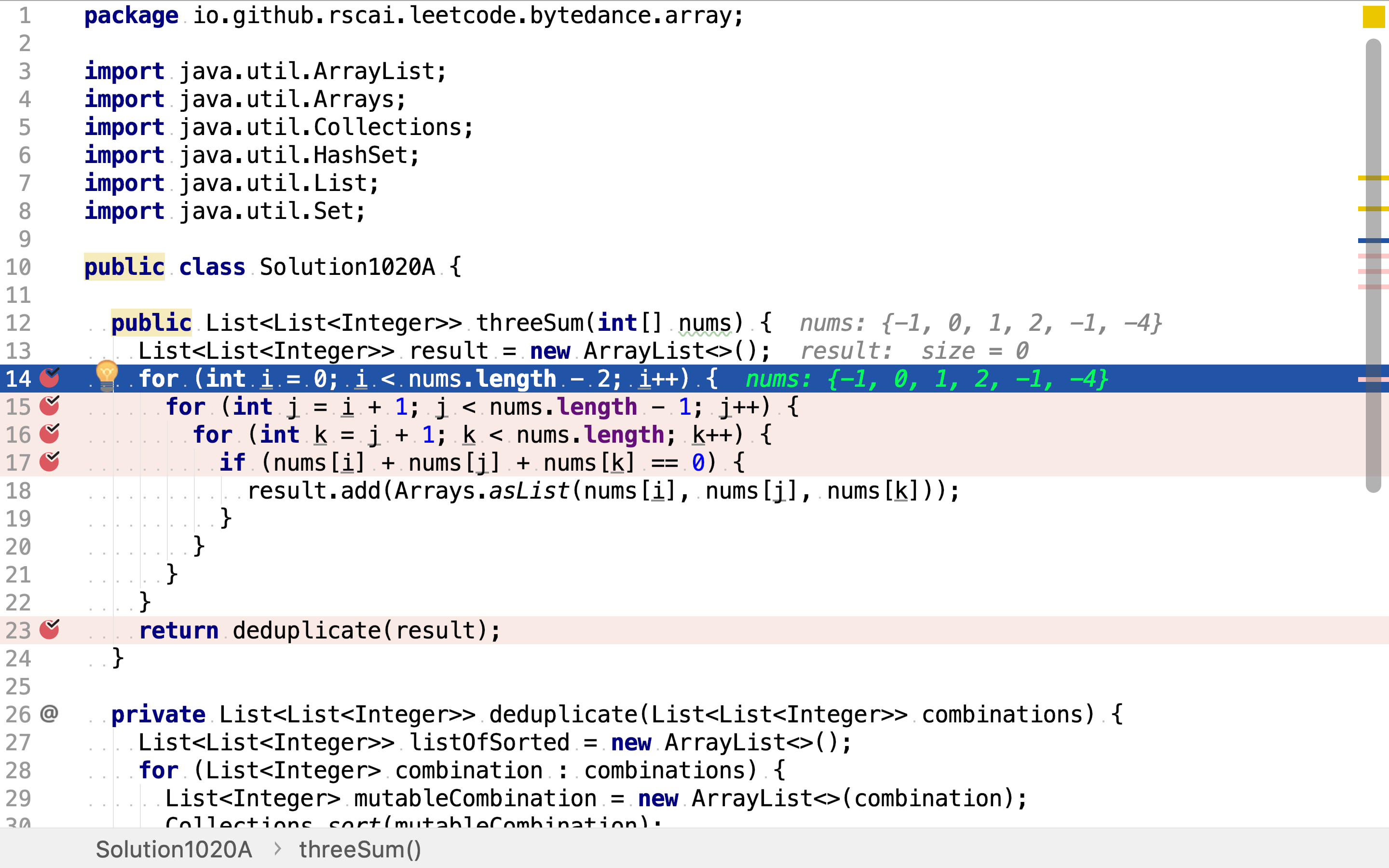
然后,从第一个整数之后的剩余整数中罗列三元组中第二个整数的所有选择。
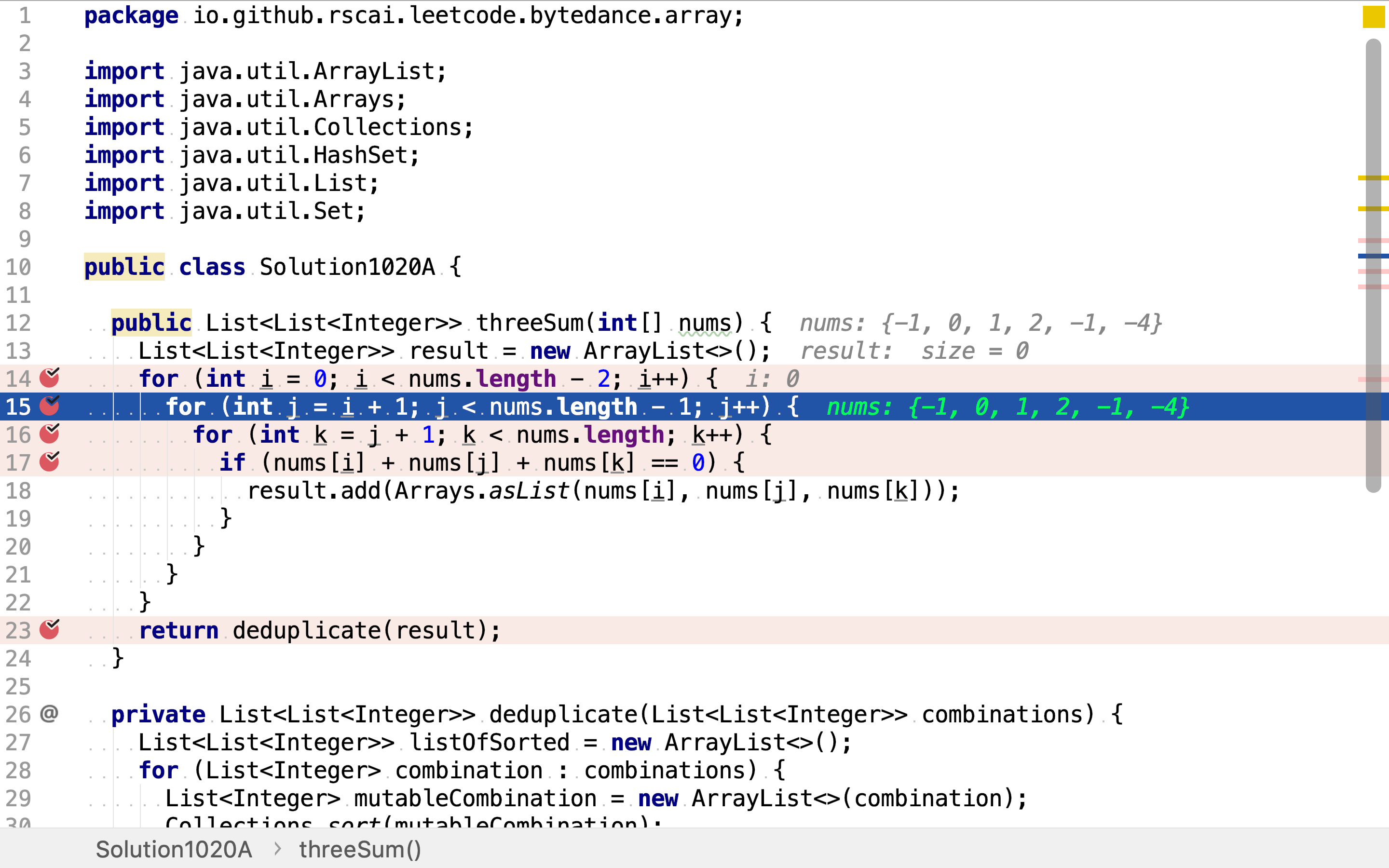
再然后,从第二个整数之后的剩余整数中罗列三元组中第三个整数的所有选择。
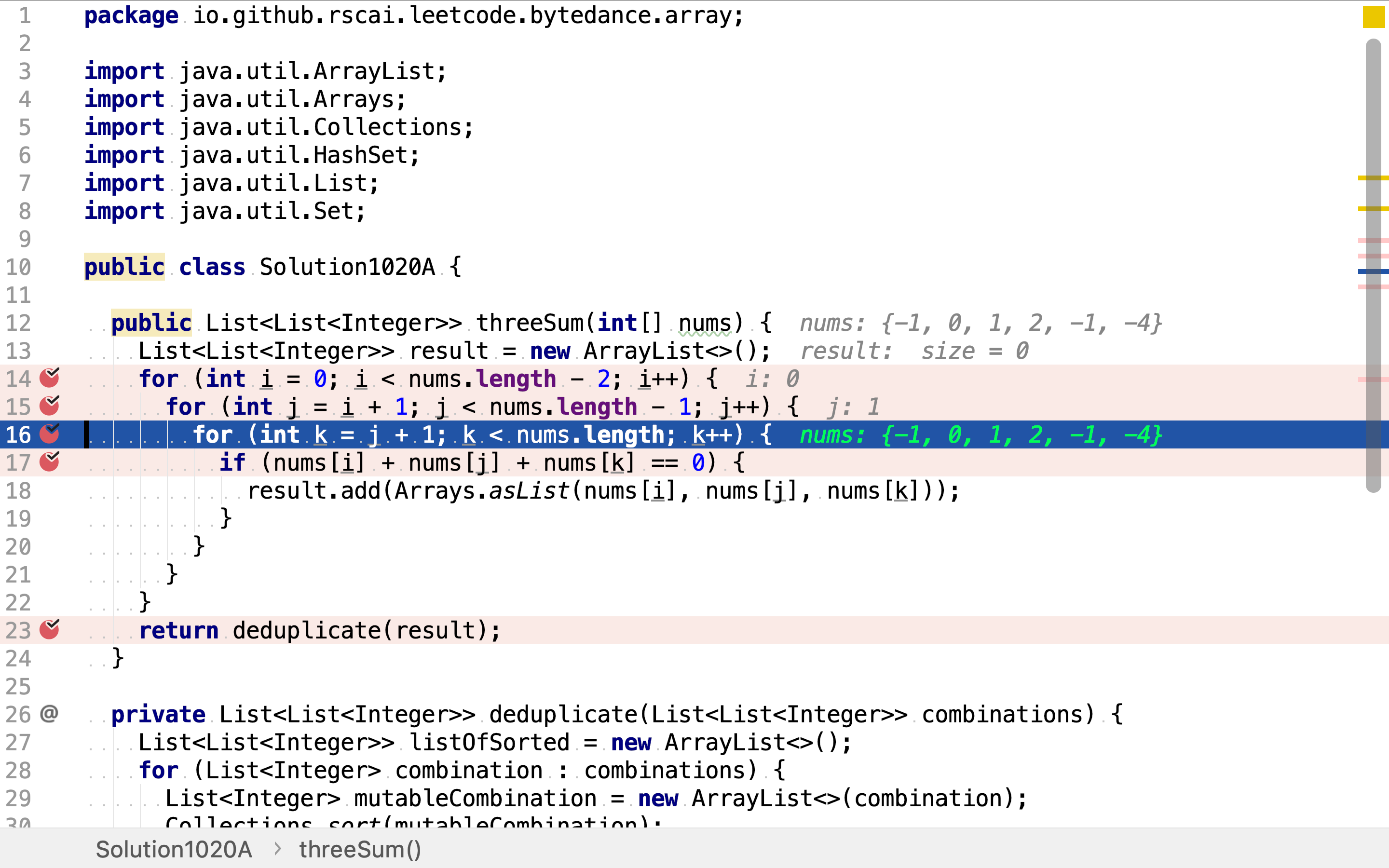
罗列出三元组后,再逐一检测其和是否为0。
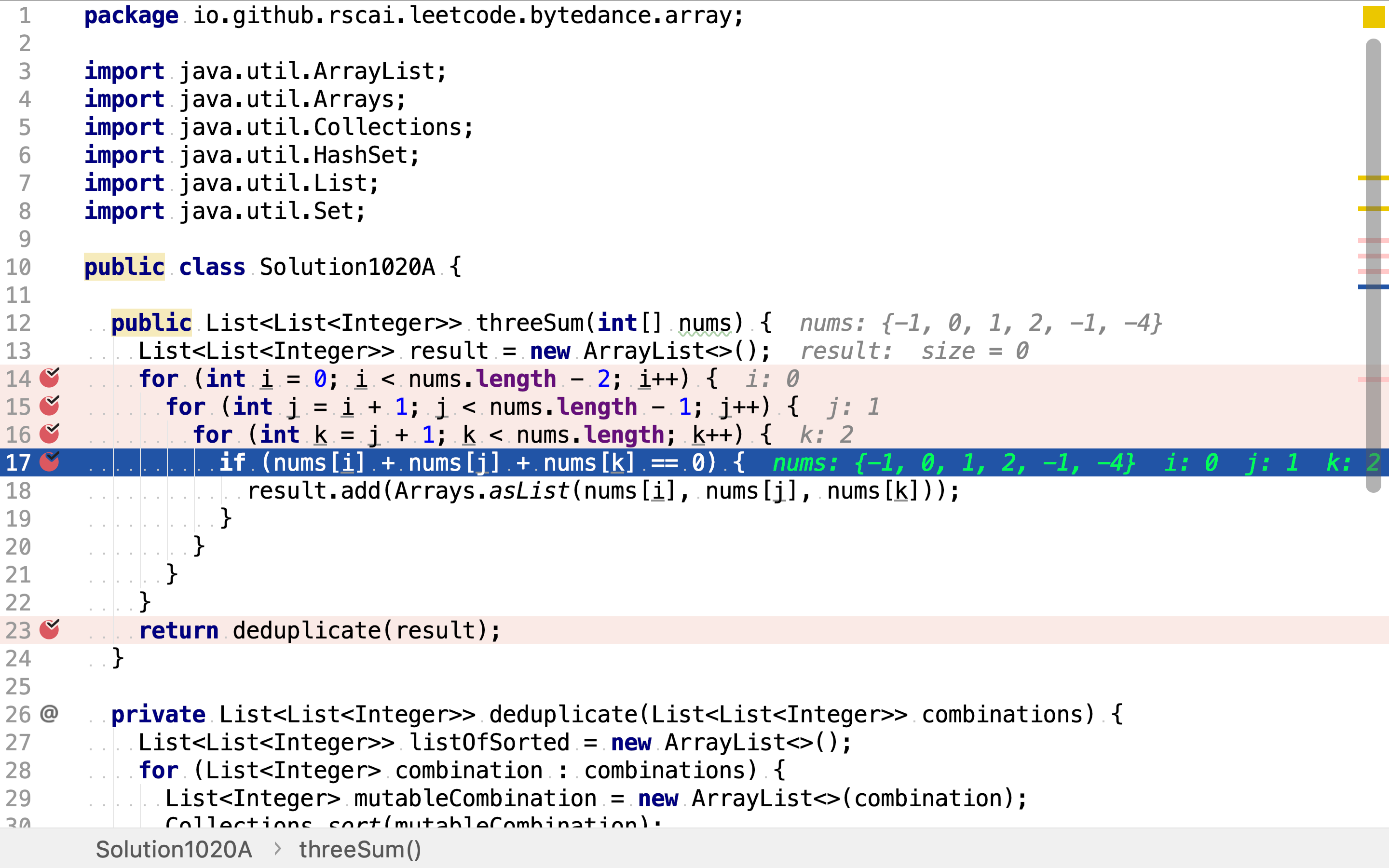
最后,再去除重复的三元组。在罗列所有三元组时已经避免了由重复元素组成的三元组,但不同的元素可以包含相同的整数值,所以依旧需要去一次重复。
复杂度分析
时间复杂度
其罗列了所有的组合,所有组合数为。所以,时间复杂度为:
空间复杂度
最多有个三元组。空间复杂度为:
排序加双指针法
先对无序的输入数组排序。然后以穷举法罗列出三元组中第一个整数的所有取值可能。因为整数序列是有序递增的,且第二个及第三个整数一定不小于第一个整数。所以,如果第一个整数大于0:
- 则第二个和第三个整数也大于0,其和一定也大于0。
- 以第一个整数后续整数为第一个整数的三元组和一定大于0。
所以,在罗列第一个整数所有取值时可以直接排除大于0及其后续的整数。
举个例子,给定数组[-1, 0, 1, 2, -1, -4]。按升序排序后得到[-4, -1, -1, 0, 1, 2]。第一个整数的可选取值有-4, -1, -1, 0。
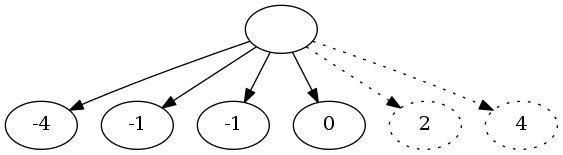
所求三元组的和为0,所以第二个和第三个整数的和等于第一个整数的负值。
举个例子,假设第一个整数是-4,第二个和第三个整数的和需为4。分别使用两个指针second和third指向第二个和第三个整数,second从剩余有序整数序列头部开始,third从剩余有序整数序列尾部开始。头部和尾部整数的和为3,小于所求值4。
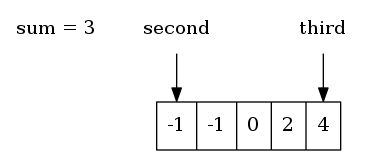
因为剩余整数序列是有序的,所有有以下性质:
- 当
second向后移动一位,third固定不变,则两个指针所指整数的和会增大
- 当
third向前移动一位,second固定不变,则两个指针所指整数的和会减小
所以,当发现第二个和第三个整数和小于期望值时,应将second指针向后移动一位。
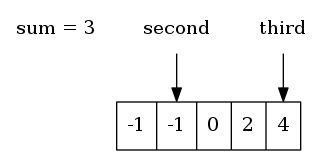
为去除重复三元组,相同值不应在同一位置出现多次。所以,此时应略过第二个-1,将second继续后移一位。
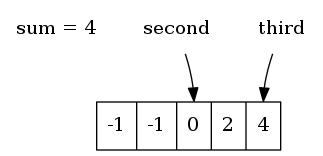
第二个和第三个整数的和为4,找到了个和为0的三元组。将second和third指针分别向后和向前移动一位,以寻找其它拥有相同「第一个整数」的三元组。
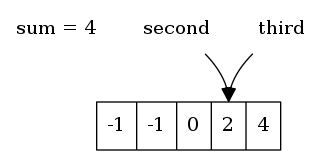
second和third指针指向了同一个元素,这表明已组探索了所有可行的第二个和第三个整数组合。
代码
package io.github.rscai.leetcode.bytedance.array;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.List;
public class Solution1020B {
public List<List<Integer>> threeSum(int[] nums) {
List<Integer> sortedNums = new ArrayList<>();
for (int num : nums) {
sortedNums.add(num);
}
Collections.sort(sortedNums);
List<List<Integer>> result = new ArrayList<>();
for (int firstIndex = 0; firstIndex < sortedNums.size() - 2; firstIndex++) {
if (sortedNums.get(firstIndex) > 0) {
break;
}
if (firstIndex > 0 && sortedNums.get(firstIndex).equals(sortedNums.get(firstIndex - 1))) {
continue;
}
int secondIndex = firstIndex + 1;
int thirdIndex = sortedNums.size() - 1;
while (thirdIndex > secondIndex) {
if (secondIndex > firstIndex + 1 && sortedNums.get(secondIndex)
.equals(sortedNums.get(secondIndex - 1))) {
secondIndex++;
continue;
}
if (thirdIndex < sortedNums.size() - 1 && sortedNums.get(thirdIndex).equals(sortedNums
.get(thirdIndex + 1))) {
thirdIndex--;
continue;
}
int sum = sortedNums.get(firstIndex) + sortedNums.get(secondIndex) + sortedNums.get(thirdIndex);
if (sum == 0) {
result.add(Arrays
.asList(sortedNums.get(firstIndex), sortedNums.get(secondIndex), sortedNums.get(thirdIndex)));
secondIndex++;
thirdIndex--;
} else if (sum < 0) {
secondIndex++;
} else {
thirdIndex--;
}
}
}
return result;
}
}
首先,对整数序列按升序排序。
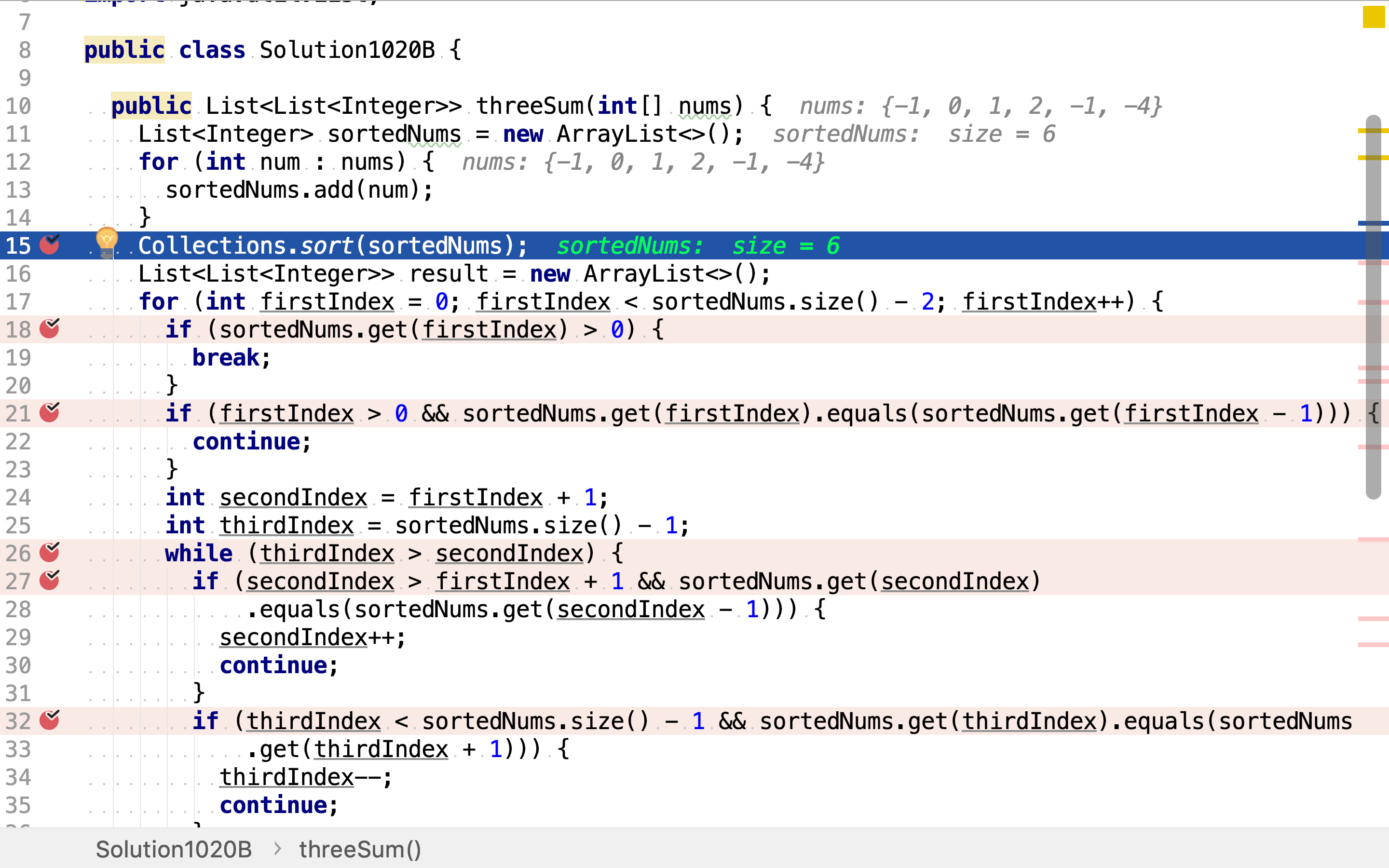
然后,从小到大罗列三元组中第一个整数的所有可能取值。如果第一个整数都已经大于0,则可直接排除。
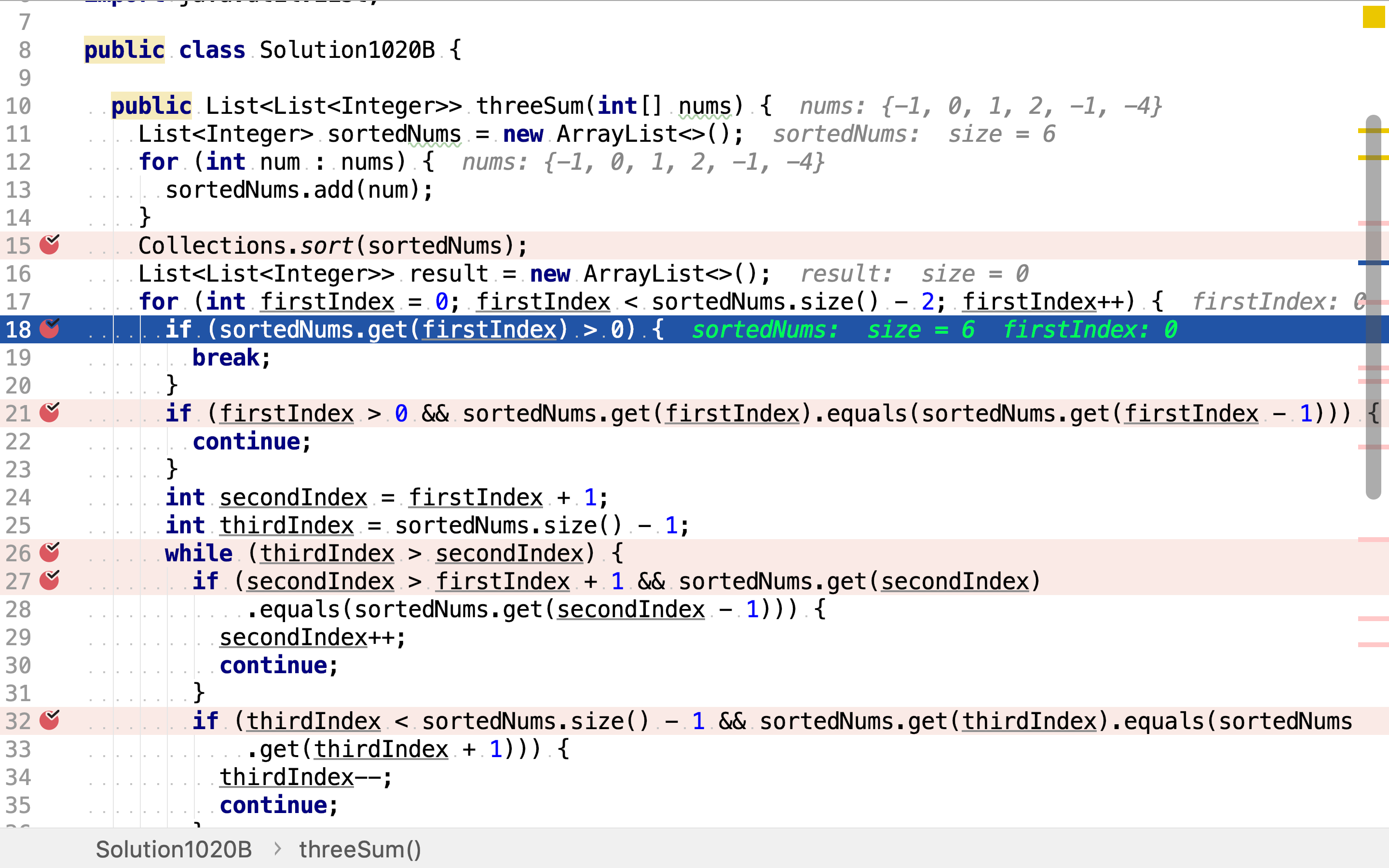
再然后,跳过重复的「第一个整数」取值,三元组中不同位置可以出现相同的值,但同一个位置不能出现重复的值。
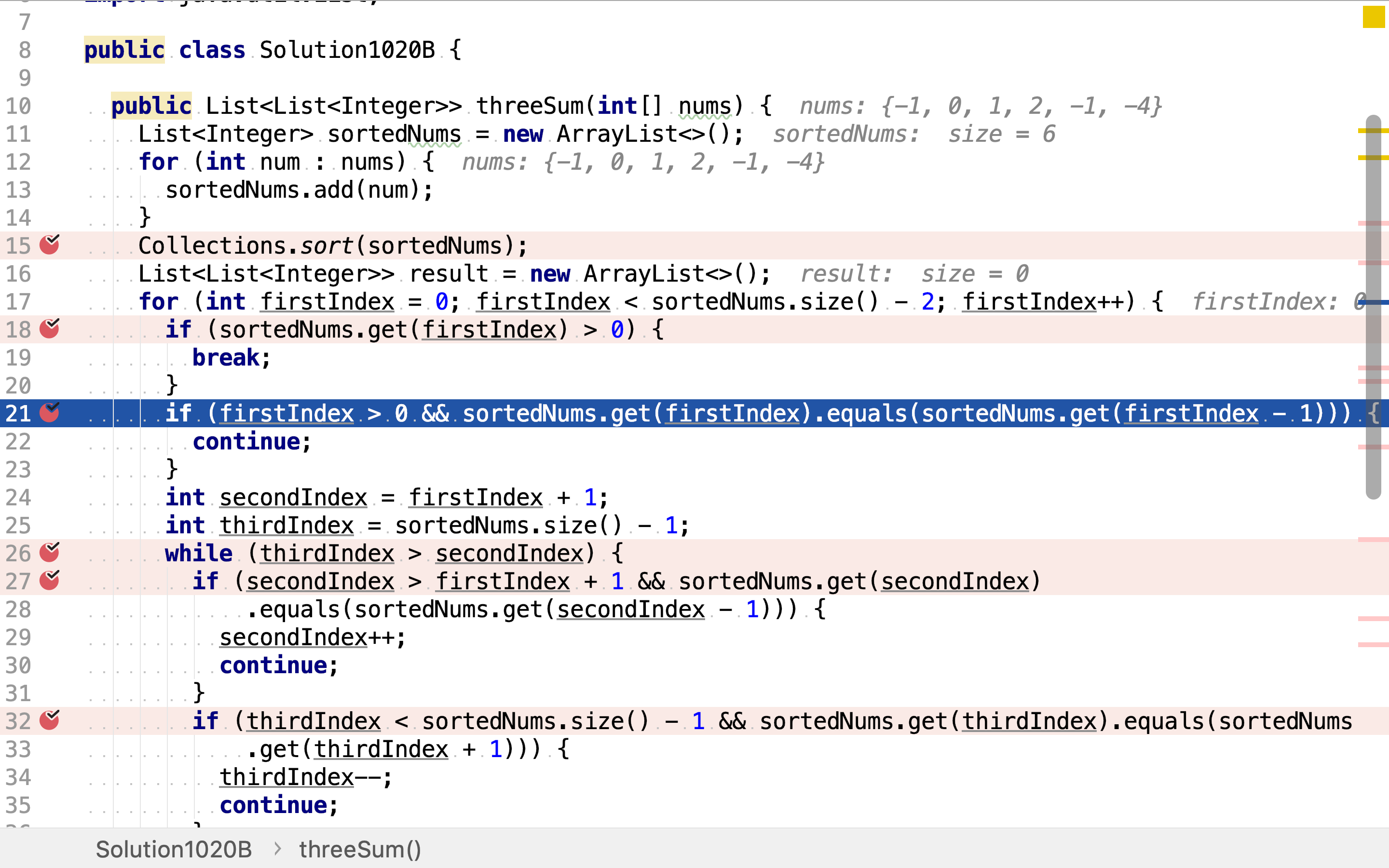
再然后,使用双指针探索第二个和第三个整数的组合。
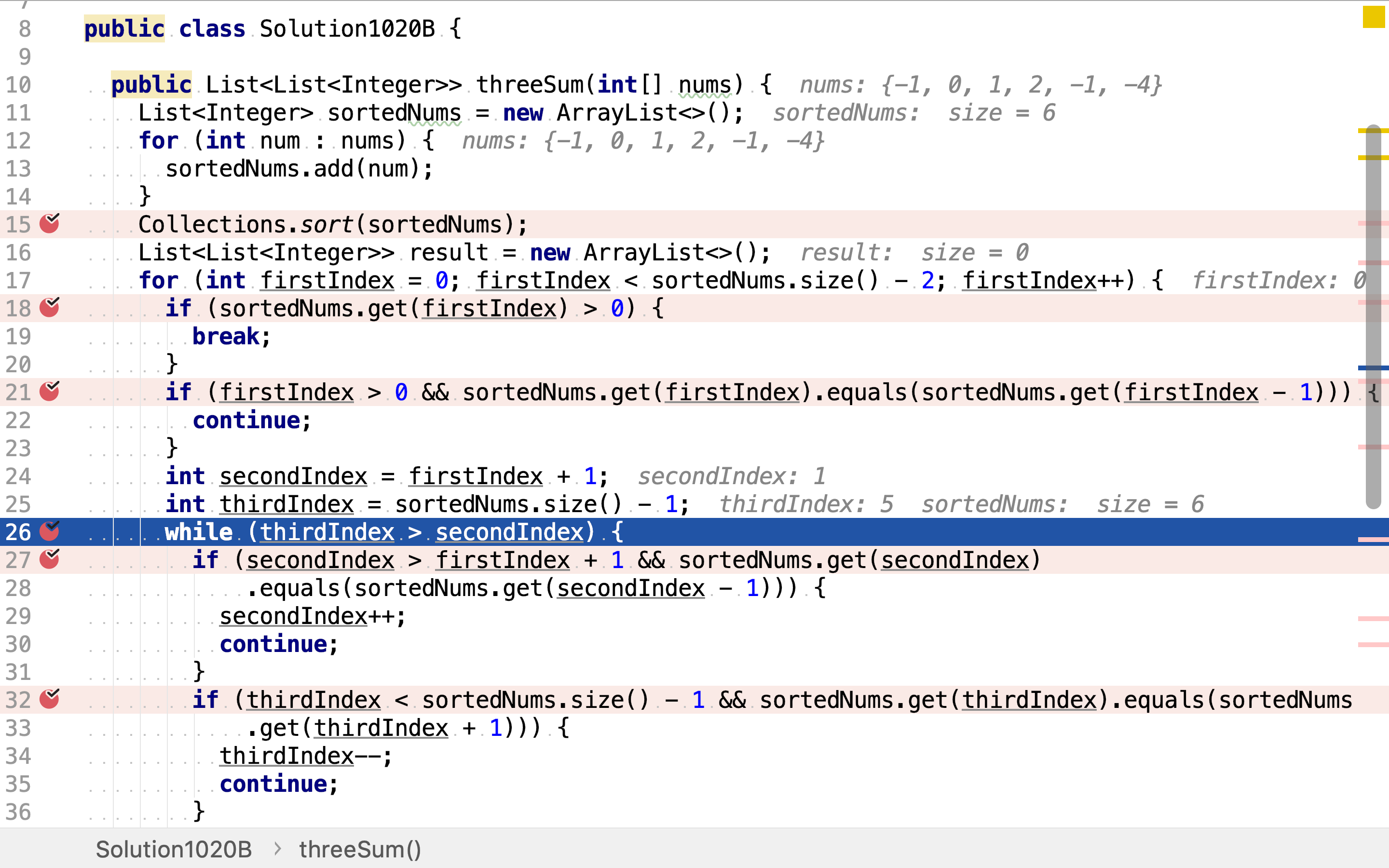
跳过重复的「第二个整数」。
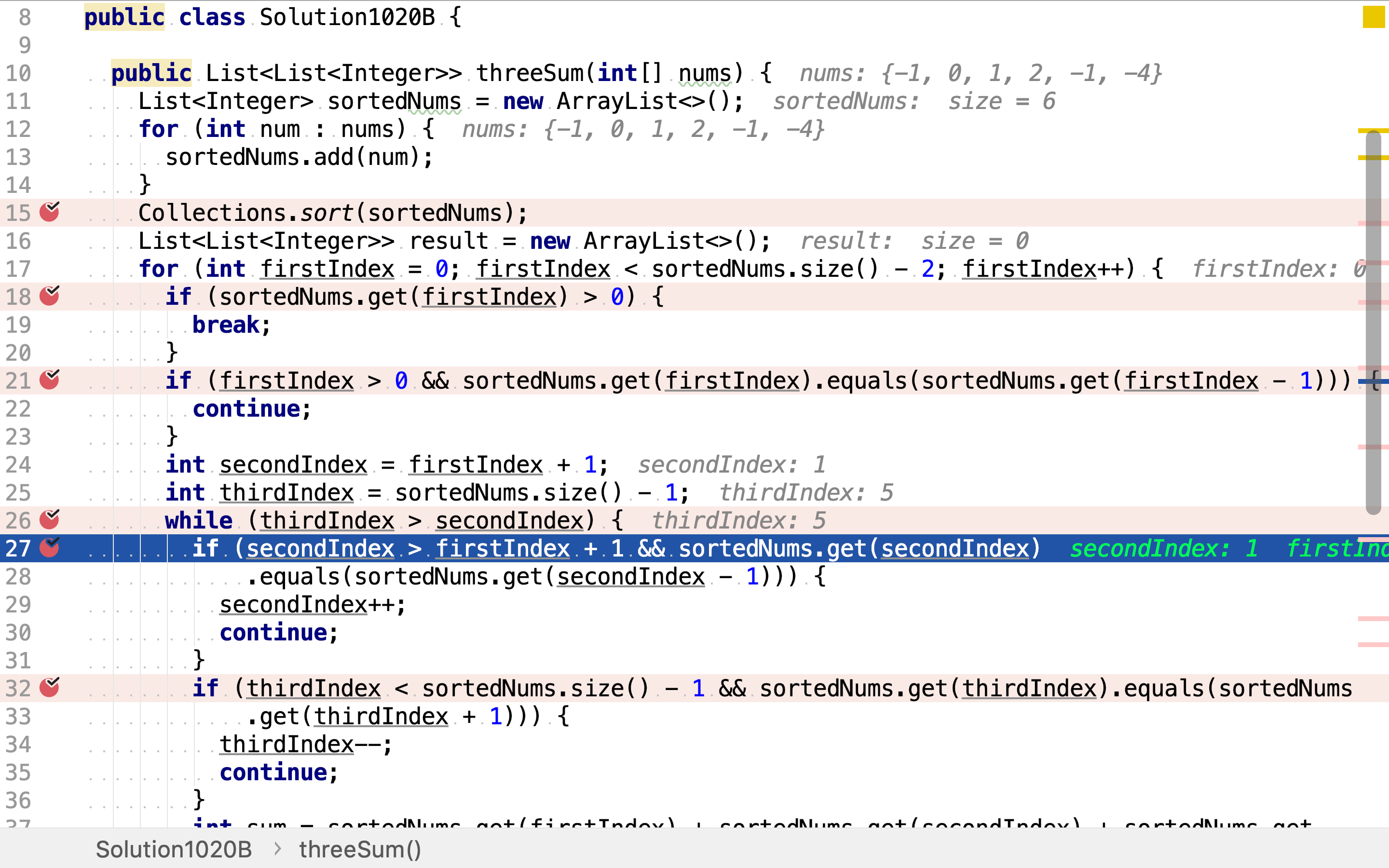
跳过重复的「第三个整数」。
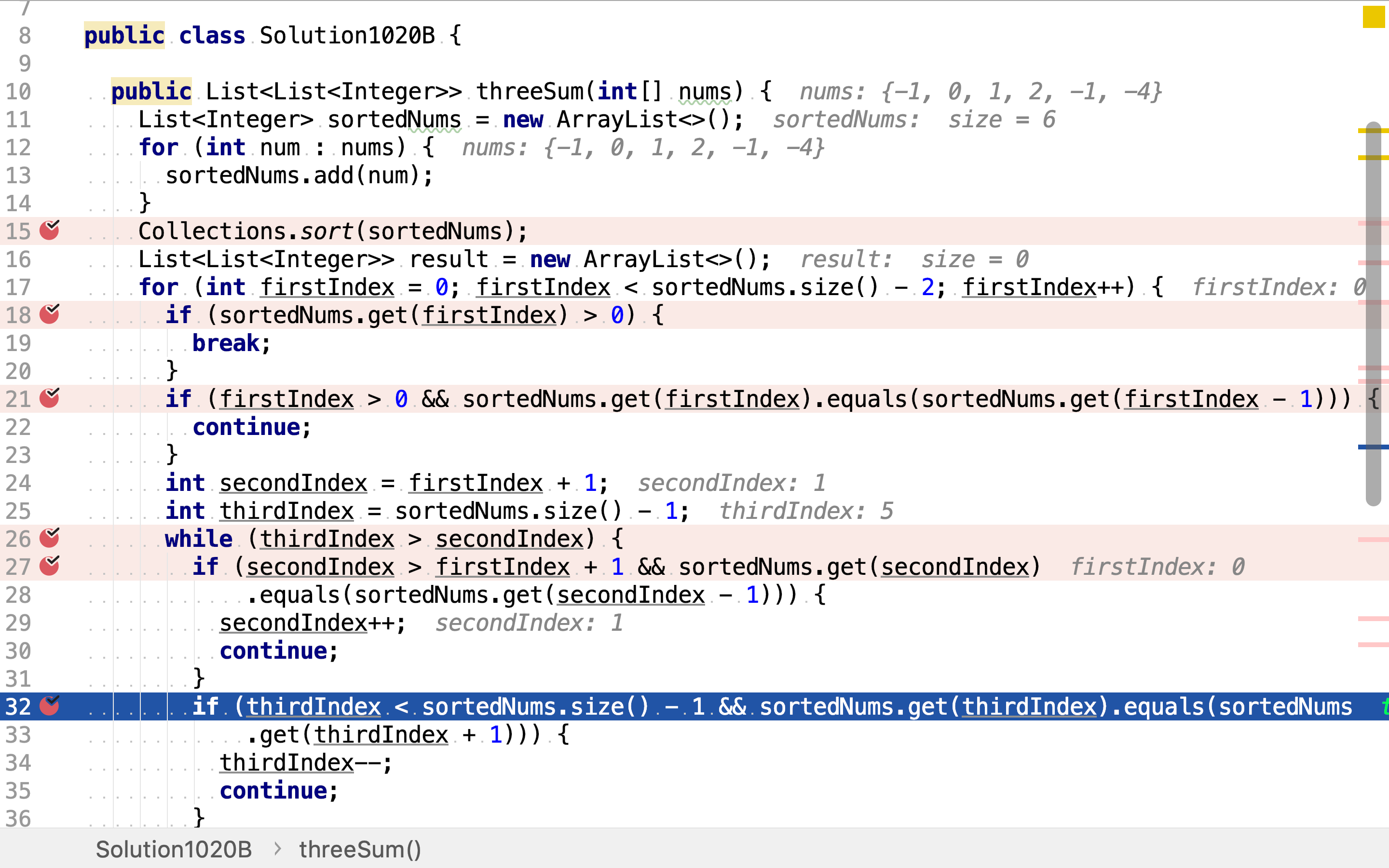
如果三整数和为0,则意味着找到一个符合要求的「三元组」,second和third指针分别向后和向前移动一位。
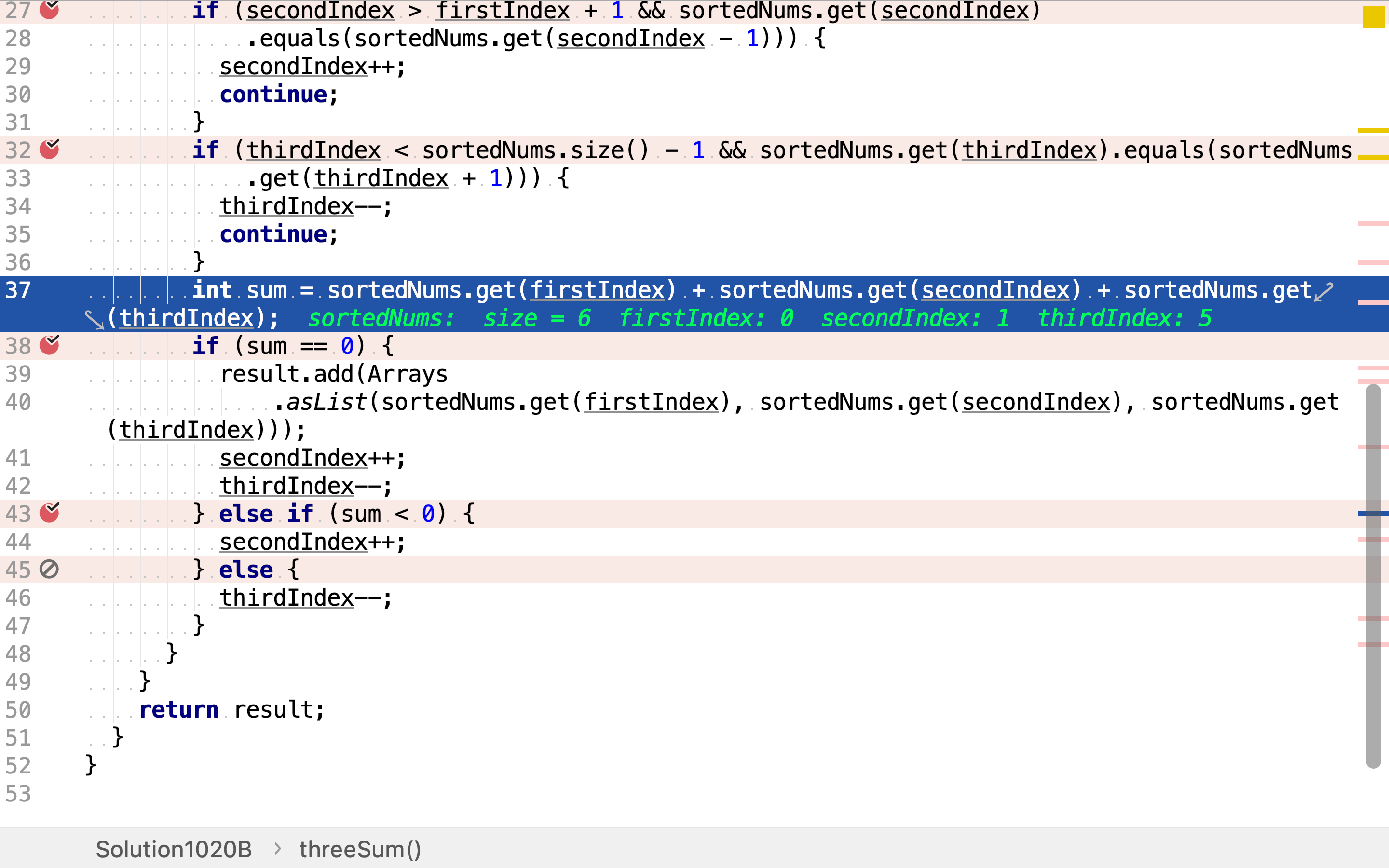
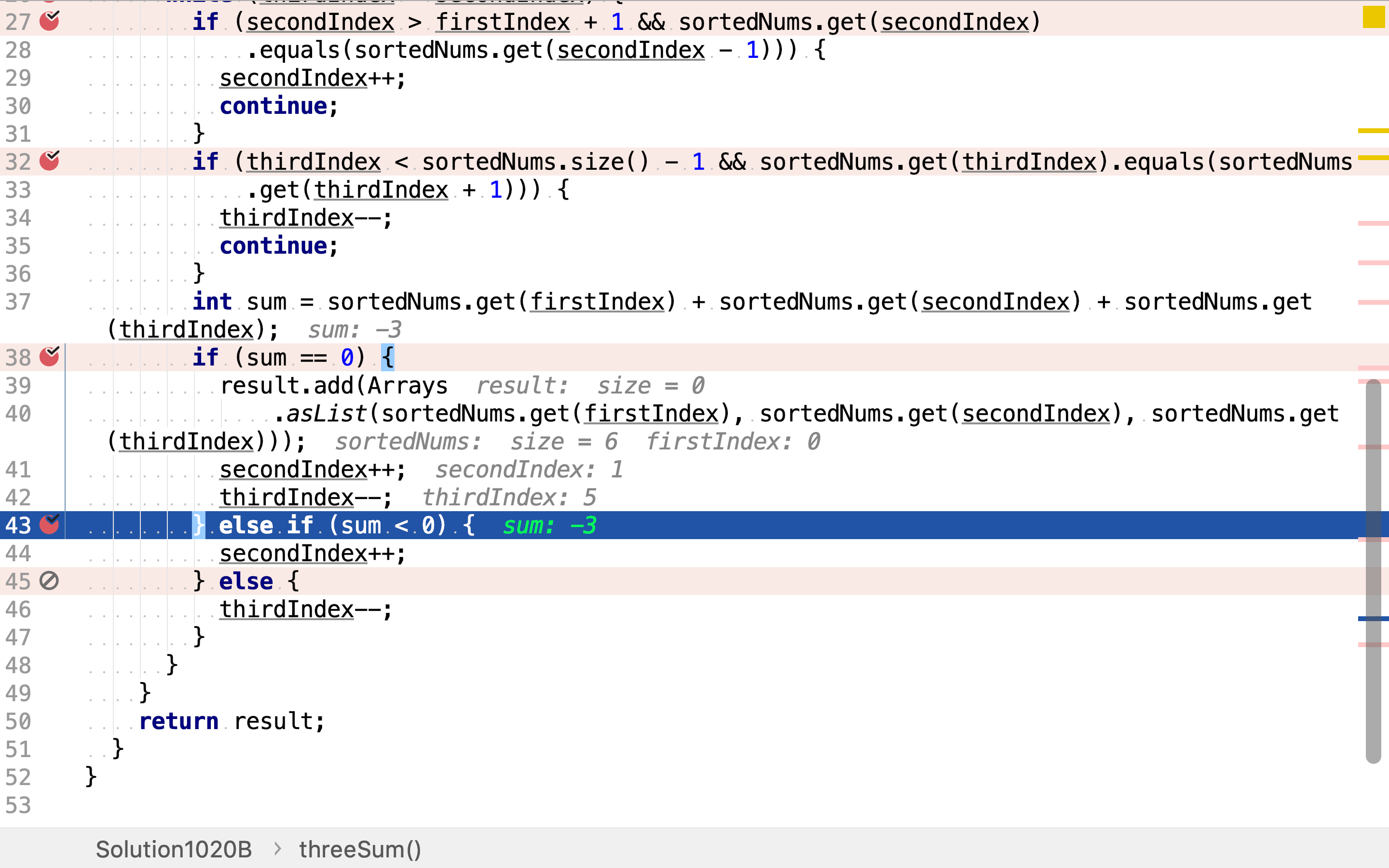
如果三整数和小于0,意味着第二个和第三个整数的和过小,将second指针向后移一位。
如果三整数和大于0,意味着第二个和第三个整数的和过大,将third指针向前移一位。
复杂度分析
时间复杂度
JDK实现的「快速排序」时间复杂度为。在罗列第一个整数时遍历了一遍整数序列。针对每一个「第一个整数」取值,其仅遍历一遍剩余序列就得到了所有可行的第二个和第三个整数组合。所以,整体时间复杂度为:
空间复杂度
构造了一个有序的整数序列,使用用了三个指针分别指向第一、第二和第三个整数,还保存了所有可行的三元组(最多可达个三元组)。所以,空间复杂度为:


















