岛屿的最大面积

题目

给定一个包含了一些 0 和 1的非空二维数组grid, 一个 岛屿 是由四个方向 (水平或垂直) 的 1 (代表土地) 构成的组合。你可以假设二维矩阵的四个边缘都被水包围着。

找到给定的二维数组中最大的岛屿面积。 (如果没有岛屿，则返回面积为0。)

示例1：

[[0,0,1,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,1,1,0,1,0,0,0,0,0,0,0,0],
[0,1,0,0,1,1,0,0,1,0,1,0,0],
[0,1,0,0,1,1,0,0,1,1,1,0,0],
[0,0,0,0,0,0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,0,1,1,0,0,0,0]]

对于上面这个给定矩阵应返回6。注意答案不应该是11，因为岛屿只能包含水平或垂直的四个方向的‘1’。

示例2：

[[0,0,0,0,0,0,0,0]]

对于上面这个给定的矩阵, 返回0。

注意: 给定的矩阵grid的长度和宽度都不超过50。

深度优先搜寻法

地图中的岛屿可以视为图，求最大的岛屿即为求最大的连通分量。依次以图中每个点为起点遍历图，即可获取所有连通分量。

深度优先搜寻

深度优先搜寻演算法（英语：Depth-First-Search，DFS）是一种用于遍历或搜寻树或图的演算法。沿着树的深度遍历树的节点，尽可能深的搜寻树的分支。当节点v的所在边都己被探寻过，搜寻将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个行程反覆进行直到所有节点都被存取为止。属于盲目搜寻。

实现方法

  1. 首先将根节点放入伫列中。
  2. 从伫列中取出第一个节点，并检验它是否为目标。
    • 如果找到目标，则结束搜寻并回传结果。
    • 否则将它某一个尚未检验过的直接子节点加入伫列中。
  3. 重复步骤2。
  4. 如果不存在未检测过的直接子节点。
    • 将上一级节点加入伫列中。
    • 重复步骤2。
  5. 重复步骤4。
  6. 若伫列为空，表示整张图都检查过了——亦即图中没有欲搜寻的目标。结束搜寻并回传「找不到目标」。

举个例子，给定如下以二维整数数组表示的图：

[[0,0,1,0,0,0,0,1,0,0,0,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]

依次以每个点为起点，深度优先搜寻。假设现在(1, 7)为起点进行深度优先搜寻。

[[0,0,1,0,0,0,0,1,0,0,0,0,0],
 [0,0,0,0,0,0,0,A,1,1,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]

获取(1, 7)相邻的点[(0,7),(1,8)]：

[[0,0,1,0,0,0,0,B,0,0,0,0,0],
 [0,0,0,0,0,0,0,A,1,1,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]

然后，依次以(0,7)为起点，获取未访问的相邻点。(0,7)仅有一个相邻点(0,7)但已被访问。

再然后，以(1,8)为起点，获取未访问的相邻点。(1,8)有两个相邻点，且其中(1,9)未被访问。

[[0,0,1,0,0,0,0,B,0,0,0,0,0],
 [0,0,0,0,0,0,0,A,C,D,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]

再然后，以(1,9)为起点，获取未访问的相邻点。(1,9)仅有一个相邻点但已被访问。至此，完成图中一个连通分量的深度优先搜寻。依次以图中每个点为起点，重复上述深度优先搜寻就可以遍历图中所有连通分量。

最后，从所有连通分量中取节点数最多的即为最大岛屿。

代码

package io.github.rscai.leetcode.bytedance.array; import java.util.ArrayList; import java.util.HashSet; import java.util.List; import java.util.Set; public class Solution1034A { public int maxAreaOfIsland(int[][] grid) { int rows = grid.length; int cols = grid[0].length; int maxArea = 0; for (int row = 0; row < rows; row++) { for (int col = 0; col < grid[row].length; col++) { Set<Integer> accessed = new HashSet<>(); int area = depthFirstTraversal(row, col, grid, accessed).size(); if (area > maxArea) { maxArea = area; } } } return maxArea; } private Set<Integer> depthFirstTraversal(int row, int col, int[][] grid, Set<Integer> accessed) { int rows = grid.length; int cols = grid[0].length; if (grid[row][col] == 0) { return accessed; } accessed.add(row * cols + col); List<int[]> childrenPoints = children(grid, new int[]{row, col}); for (int[] point : childrenPoints) { int address = point[0] * cols + point[1]; if (!accessed.contains(address)) { accessed.add(address); accessed = depthFirstTraversal(point[0], point[1], grid, accessed); } } return accessed; } private List<int[]> children(int[][] grid, int[] parent) { int rows = grid.length; int cols = grid[0].length; List<int[]> children = new ArrayList<>(); int row = parent[0]; int col = parent[1]; if (row - 1 >= 0 && grid[row - 1][col] == 1) { children.add(new int[]{row - 1, col}); } if (row + 1 < rows && grid[row + 1][col] == 1) { children.add(new int[]{row + 1, col}); } if (col - 1 >= 0 && grid[row][col - 1] == 1) { children.add(new int[]{row, col - 1}); } if (col + 1 < cols && grid[row][col + 1] == 1) { children.add(new int[]{row, col + 1}); } return children; } }

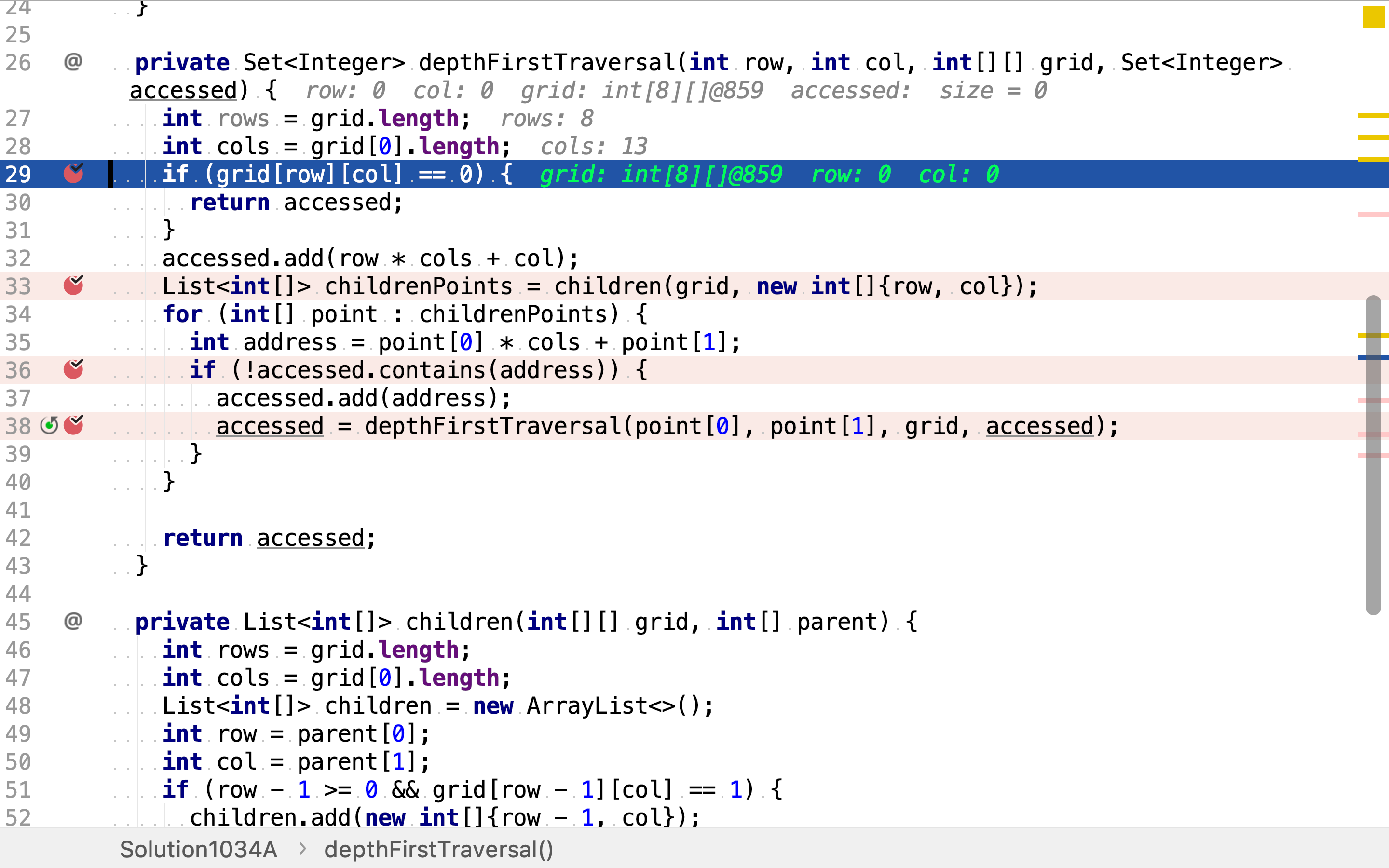
依次以每个点为起点，深度优先搜寻。

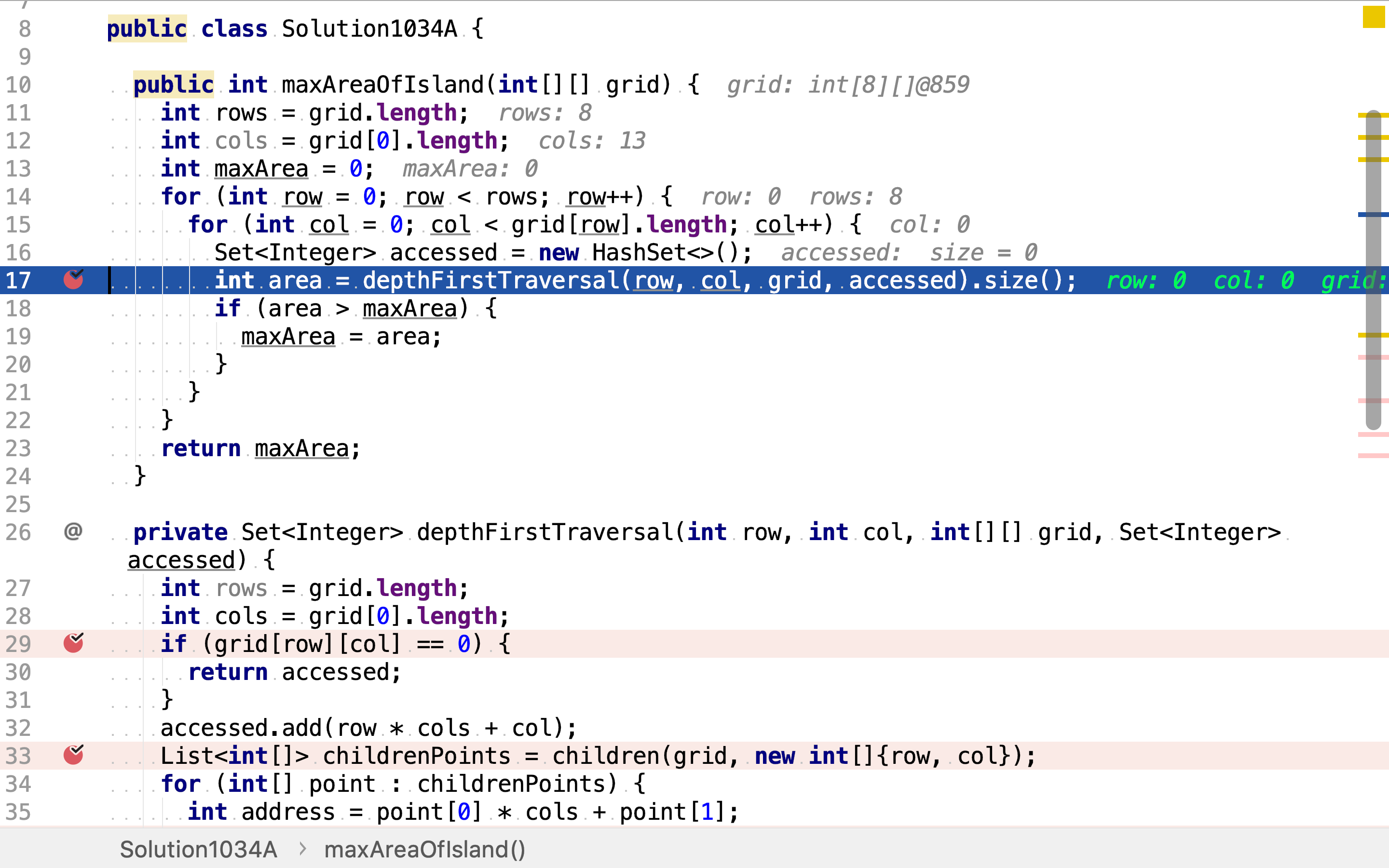
debug-A1

深度优先搜寻是一个递归方法。其先获取相邻的点，

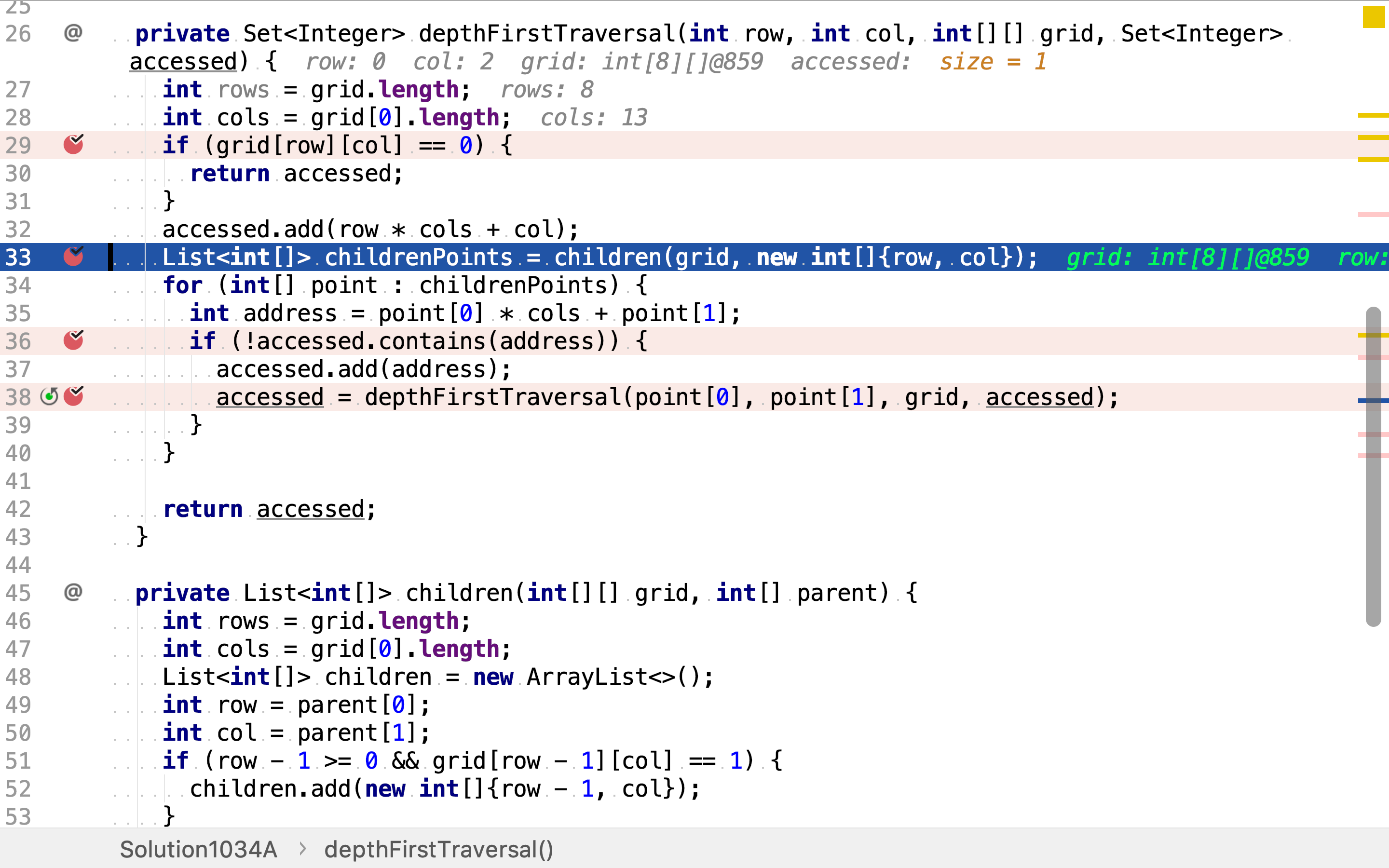
debug-A3

然后，排除掉已访问过的点。

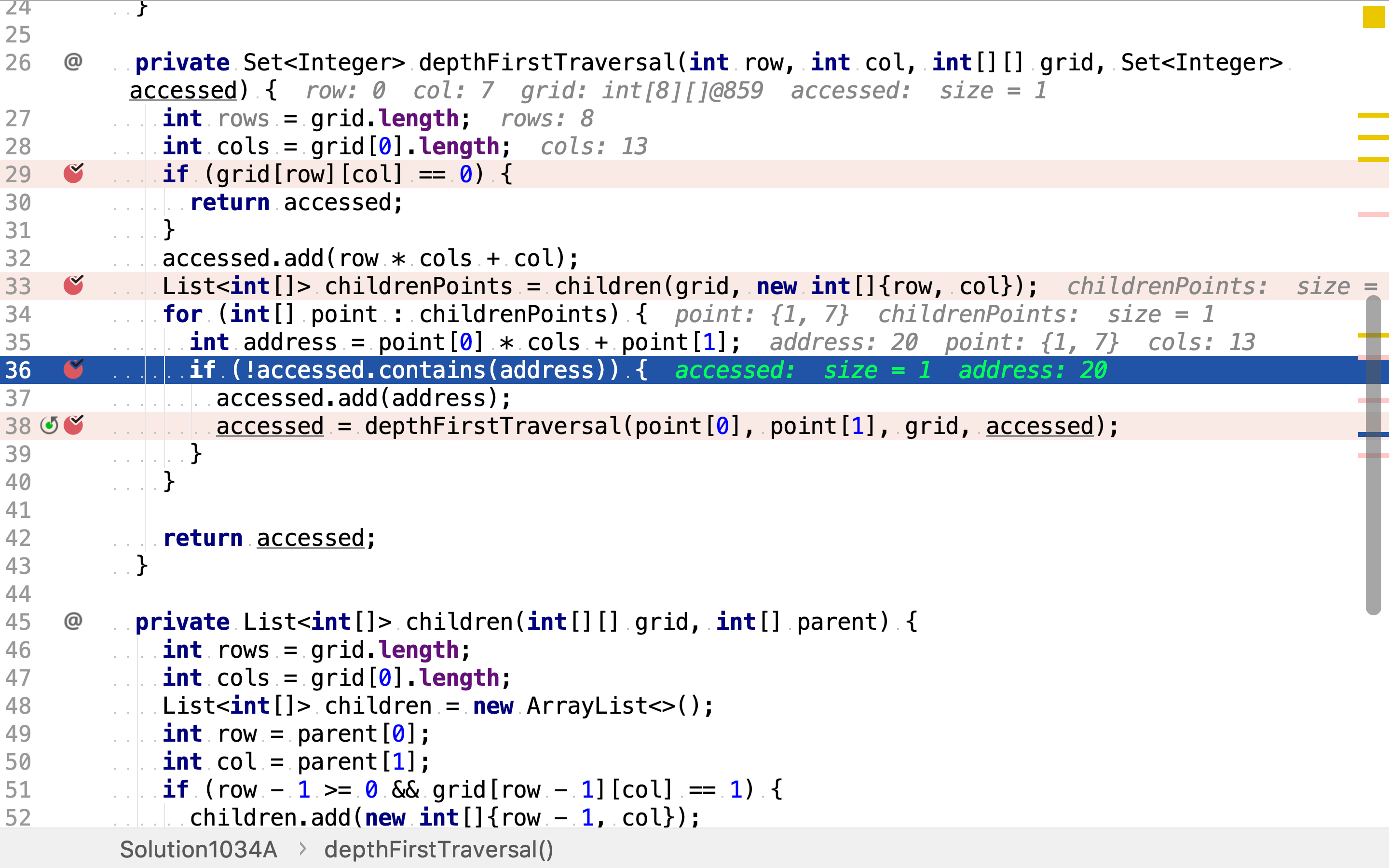
debug-A4

再然后，以相邻点为起点，递归调用深度优先搜寻。

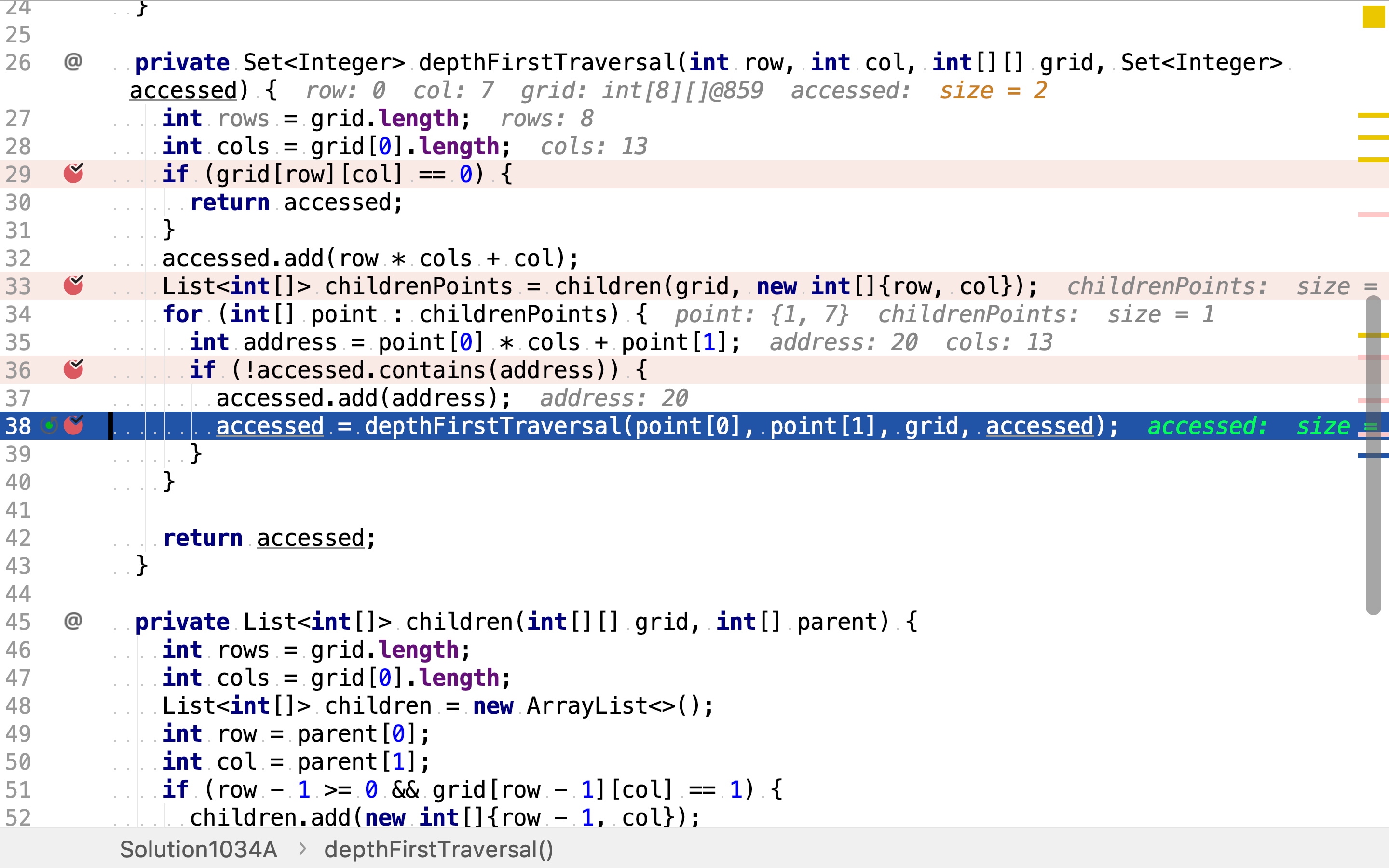
debug-A5

递归终止条件为无未访问的相邻点，或起点为空。

debug-A2

复杂度分析

时间复杂度

本演算法依次以每个点为起点深度优先搜寻。设二维数组点总数为，则其执行了次深度优先搜寻。每次深度优先搜寻最多访问了个点。所以，时间复杂度为。

空间复杂度

深度优先搜寻时保存了所有已访问过的点，其最多为。空间复杂度为。

一次遍历

在上述中演算法中，同一个连通分量会被搜寻多次。如果，在某个点被首次搜寻后将其移除，则不会有任何连通分被重复搜寻。任意点也不会被重复搜寻。

举个例子，给定如下以二维数组表示的图：

[[0,0,1,0,0,0,0,1,0,0,0,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]

按照上述演算法，连通分量[(0,7),(1,7),(1,8),(1,9)]会被搜寻四次。若在首次访问点时，即将其清除，则该分量仅会被搜寻一次。

以(0,7)为起点时，该连通分量第一次被搜寻到。

[[0,0,1,0,0,0,0,A,0,0,0,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]

获取其相邻点，同时将自身清除（置为-1）。

[[0,0,1,0,0,0,0,,0,0,0,0,0],
 [0,0,0,0,0,0,0,B,1,1,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]

继续以相邻点为起点，继续深度优先搜寻。

[[0,0,1,0,0,0,0,-1,0,0,0,0,0],
 [0,0,0,0,0,0,0,-1,-1,-1,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]

代码

package io.github.rscai.leetcode.bytedance.array; public class Solution1034B { public int maxAreaOfIsland(int[][] grid) { int rows = grid.length; int cols = grid[0].length; int maxArea = 0; for (int row = 0; row < rows; row++) { for (int col = 0; col < grid[row].length; col++) { int area = depthFirstTraversal(row, col, grid); if (area > maxArea) { maxArea = area; } } } return maxArea; } private int depthFirstTraversal(int row, int col, int[][] grid) { int rows = grid.length; int cols = grid[0].length; if (grid[row][col] == 0) { return 0; } int count = 1; grid[row][col] = -1; int[] child = oneChildren(grid, row, col); while (child != null) { grid[child[0]][child[1]] = -1; count = count + depthFirstTraversal(child[0], child[1], grid); child = oneChildren(grid, row, col); } return count; } private int[] oneChildren(int[][] grid, int row, int col) { int rows = grid.length; int cols = grid[0].length; if (row - 1 >= 0 && grid[row - 1][col] == 1) { return new int[]{row - 1, col}; } if (row + 1 < rows && grid[row + 1][col] == 1) { return new int[]{row + 1, col}; } if (col - 1 >= 0 && grid[row][col - 1] == 1) { return new int[]{row, col - 1}; } if (col + 1 < cols && grid[row][col + 1] == 1) { return new int[]{row, col + 1}; } return null; } }

依次以每个点为起点，深度优先搜寻。

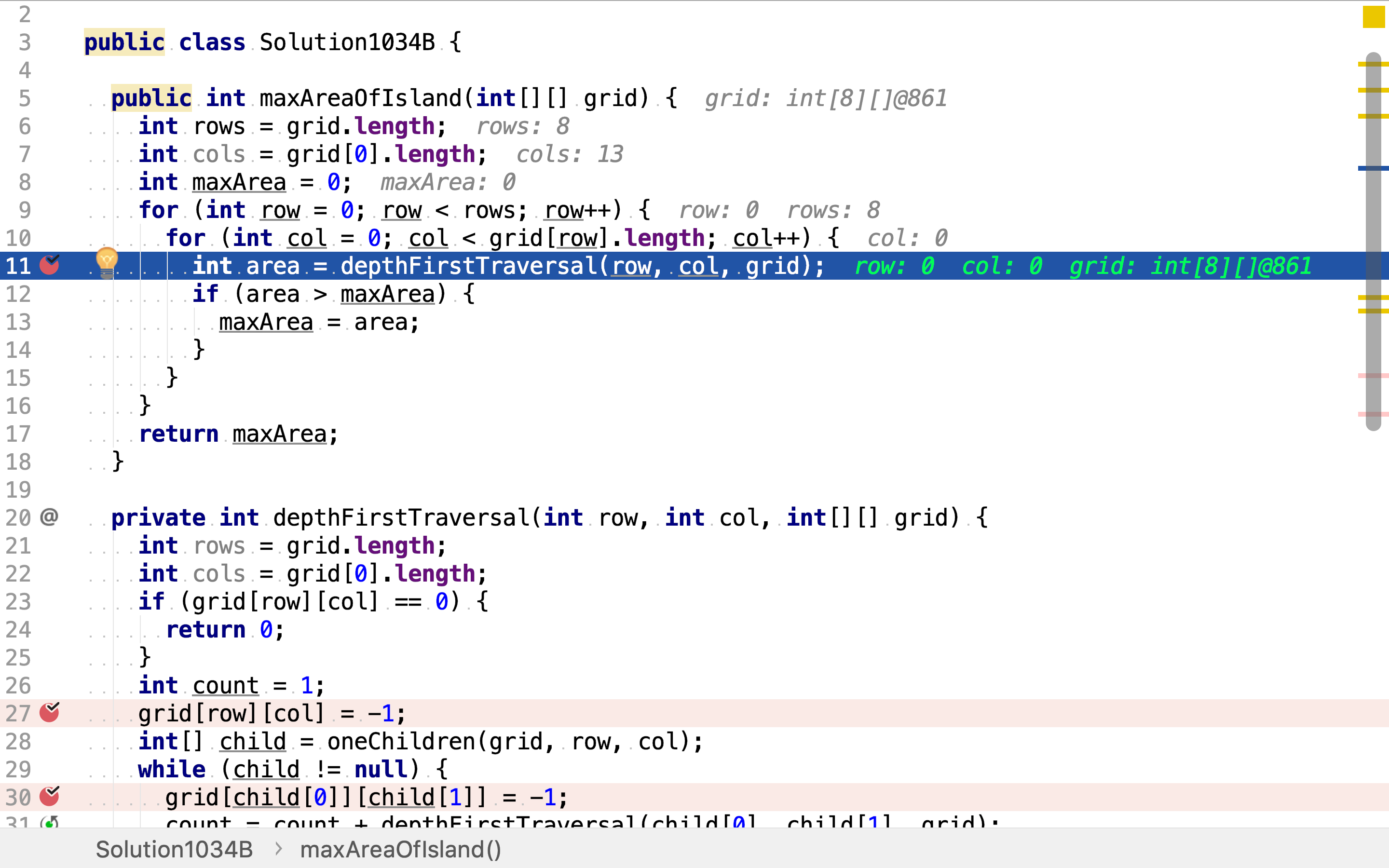
debug-B2

首次访问时点时，将其置为-1（已访问），以区分空点0。

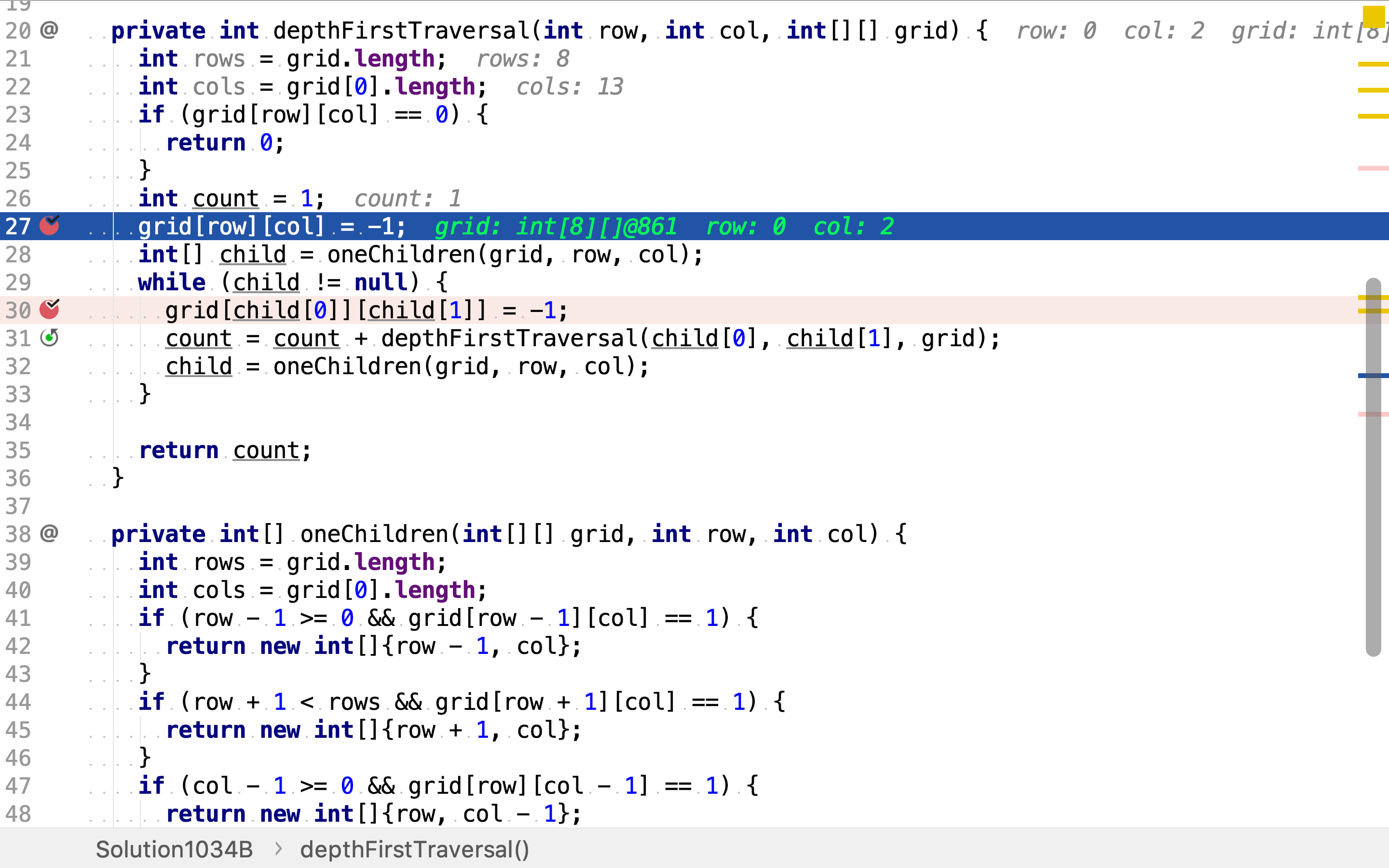
debug-B2

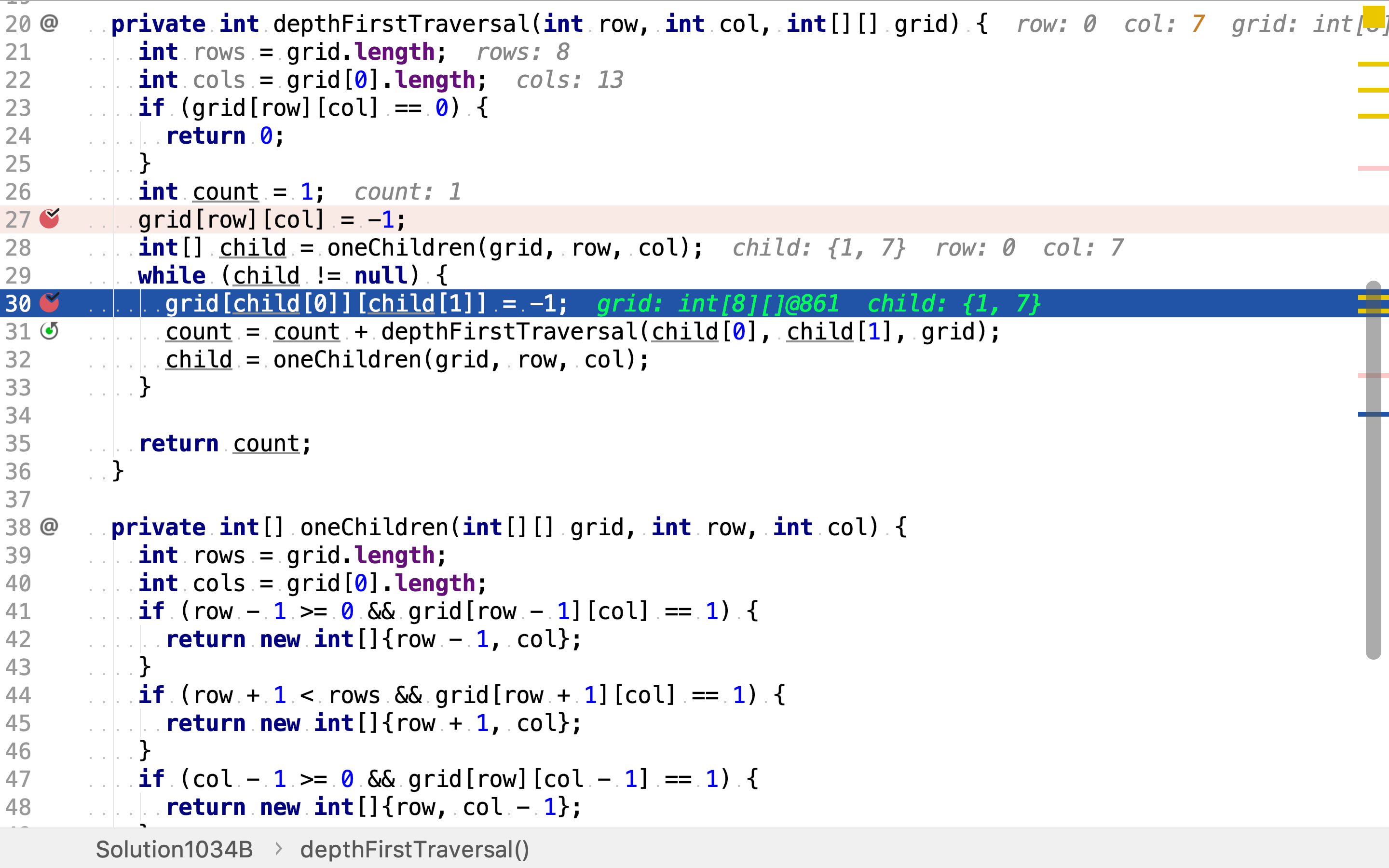
debug-B3

复杂度分析

时间复杂度

每个点至多被访问五次，第一次从1转为-1，第二至第五次被以上下左右点的相邻点被检测。时间复杂度为。

空间复杂度

每个点的已访问状态是重用输入值空间的，另外使用了常数量的变量。空间复杂度为。

参考

results matching ""

    No results matching ""