最长连续递增序列

题目

给定一个未经排序的整数数组，找到最长且连续的的递增序列。

示例 1:

输入: [1,3,5,4,7]
输出: 3
解释: 最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的，因为5和7在原数组里被4隔开。

示例 2：

输入: [2,2,2,2,2]
输出: 1
解释: 最长连续递增序列是 [2], 长度为1。

注意： 数组长度不会超过10000。

穷举法

先罗列所有的连续序列组合，再过泸出升序序列，最后计算所有升序序列长度并求出最大值。

举个例子，给定数组[1,3,5,4,7]。一组「头」「尾」位置就能唯一确定一个连续序列。「头」位置有五种选择，「尾」位置受制于「头」位置，祇能选择「头」位置及以后的位置。当「头」位置为1时，「尾」位置有五种选择；当「头」位置是3时，「尾」位置有四种选择。将所有连续序列以树的形式展现为：

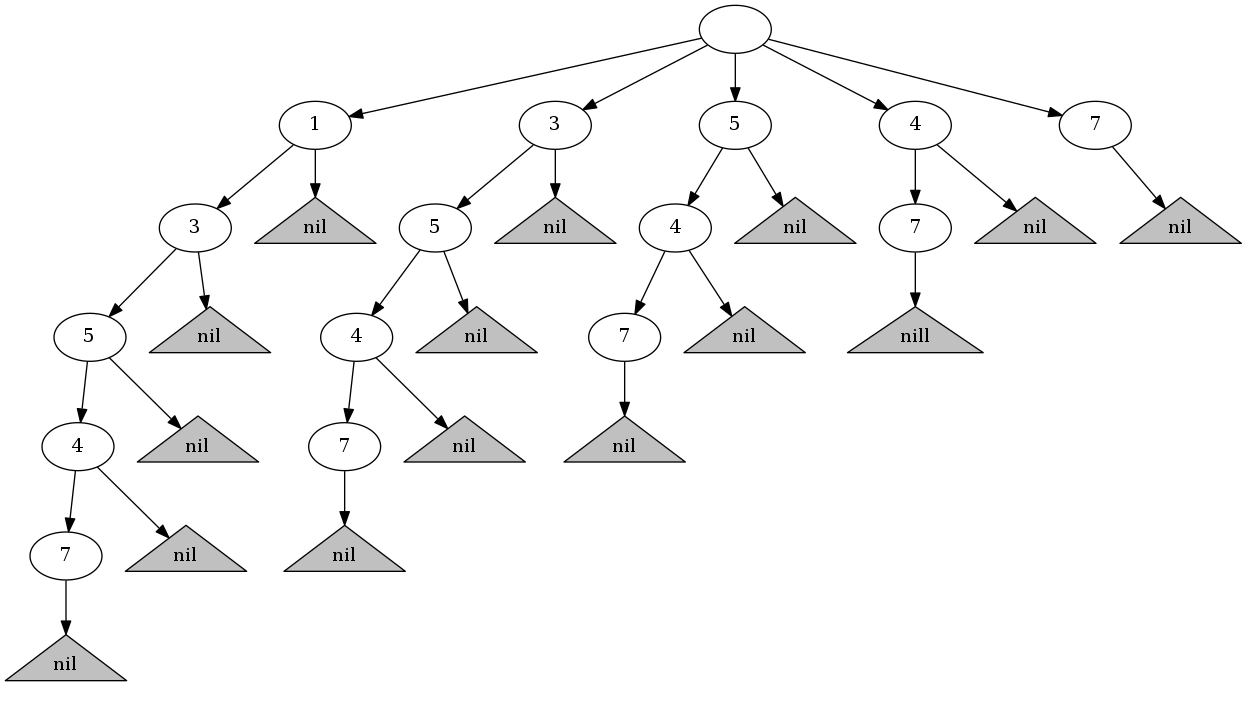
从根节点到nil叶子节点之间的路径即是一个连续序列。

代码

首先，罗列所有的「头」位置选择。

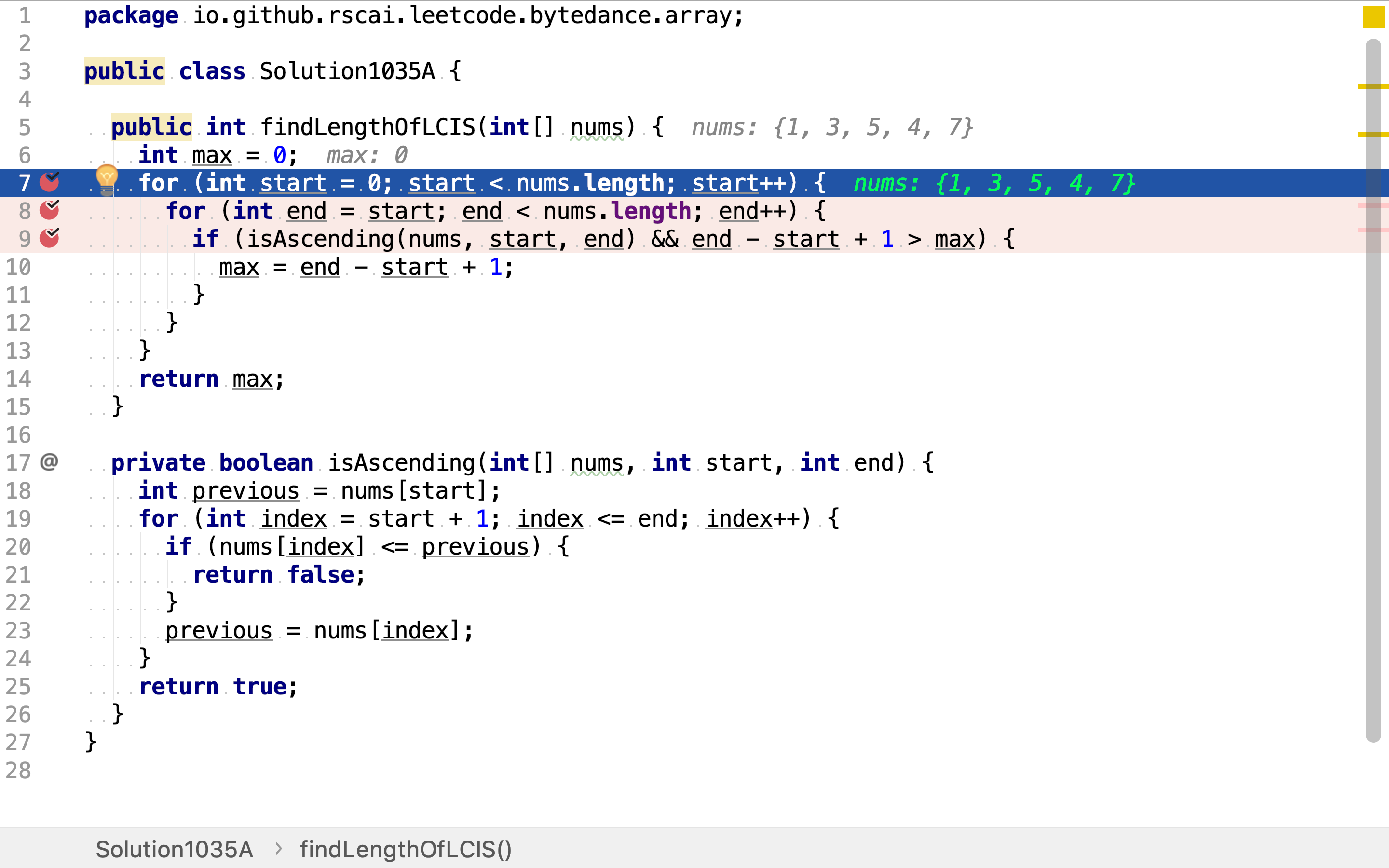
然后，依据「头」位置罗列所有「尾」位置的选择。一组「头」「尾」位置唯一确定一个连续序列。

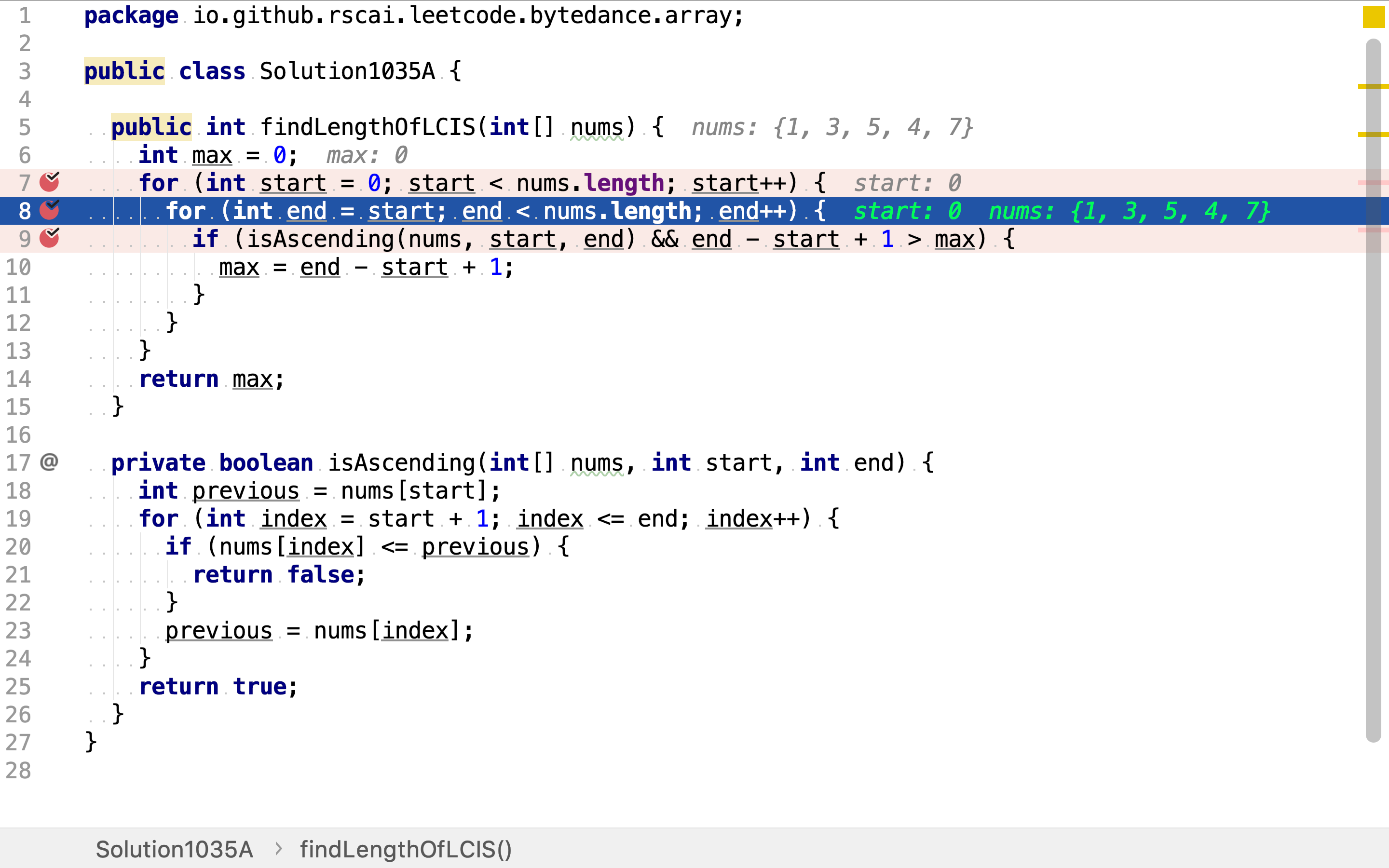
最后，过泸连续递增的序列并计算长度，其中最大长度即为所求解。

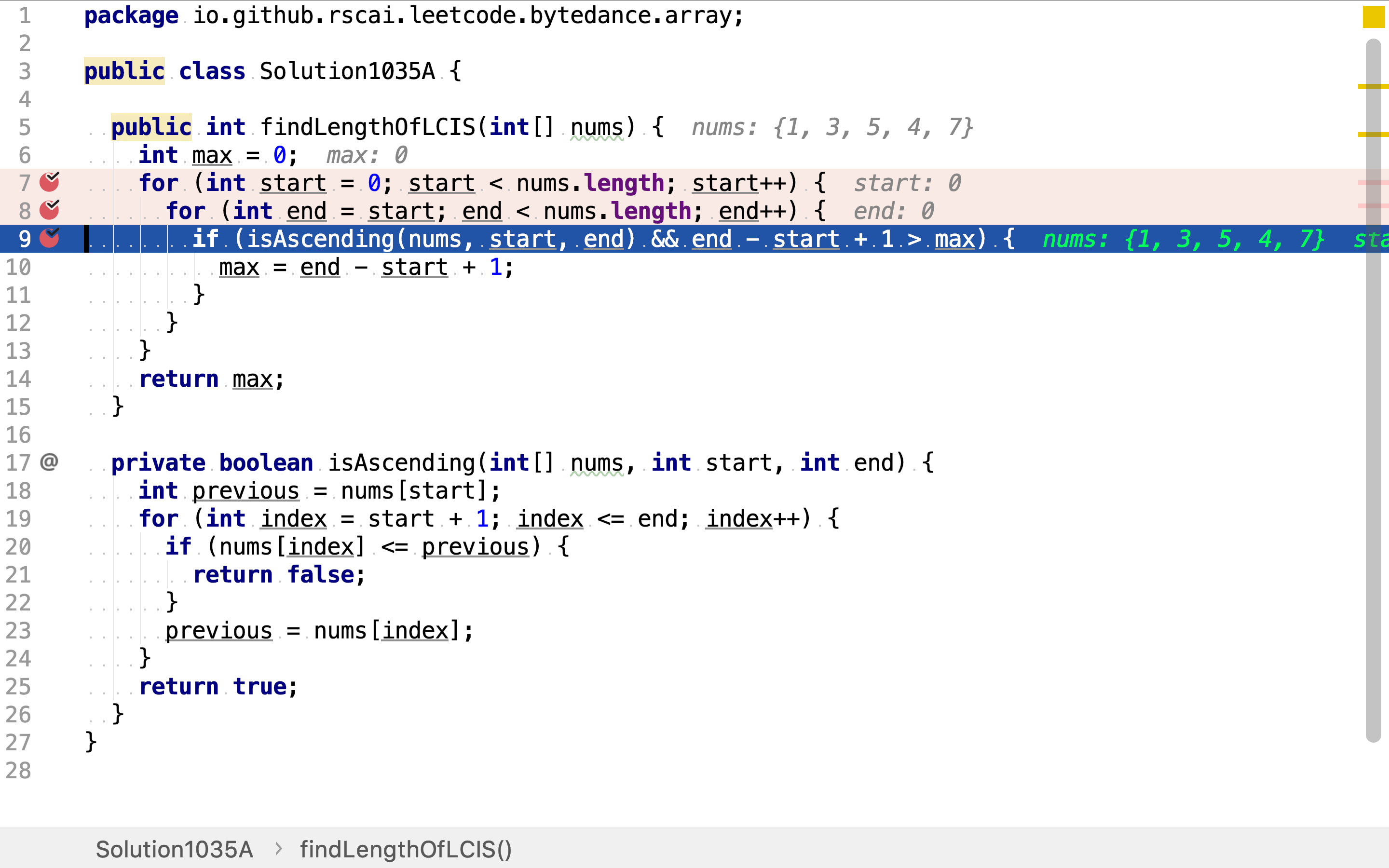
复杂度分析

时间复杂度

设数组长度为$n$，则总共有$\frac{n(n+1)}{2}$个连续序列组合。时间复杂度为$\mathcal{O}(n^2)$。

空间复杂度

使用了一个变量max，空间复杂度为$\mathcal{O}(1)$。

贪婪法

贪婪演算法（英语：greedy algorithm），又称贪心演算法，是一种在每一步选择中都採取在目前状态下最好或最佳（即最有利）的选择，从而希望导致结果是最好或最佳的演算法。比如在旅行推销员问题中，如果旅行员每次都选择最近的城市，那这就是一种贪婪演算法。

贪婪演算法在有最佳子结构的问题中尤为有效。最佳子结构的意思是局部最佳解能决定全域最佳解。简单地说，问题能够分解成子问题来解决，子问题的最佳解能递推到最终问题的最佳解。

细节

1. 建立数学模型来描述问题。
2. 把求解的问题分成若干个子问题。
3. 对每一子问题求解，得到子问题的局部最佳解。
4. 把子问题的解局部最佳解合成原来解问题的一个解。

实现该演算法的过程： 从问题的某一初始解出发；while 能朝给定总目标前进一步 do，求出可行解的一个解元素； 最后，由所有解元素组合成问题的一个可行解。

用贪婪法解本题的步骤为：

1. 求出第一毎䀆量长的连续递增子序列
2. 求出数组剩余部份中最长的连续递增子序列
3. 求第1和第2步中较长的子序列即为解

第2步递归套用1至3步。

代码

用一次遍历实现上述递归操作。从数组头部开始寻找第一个连续递增子序列，其尾部检测方法即「是否大于前方元素」。

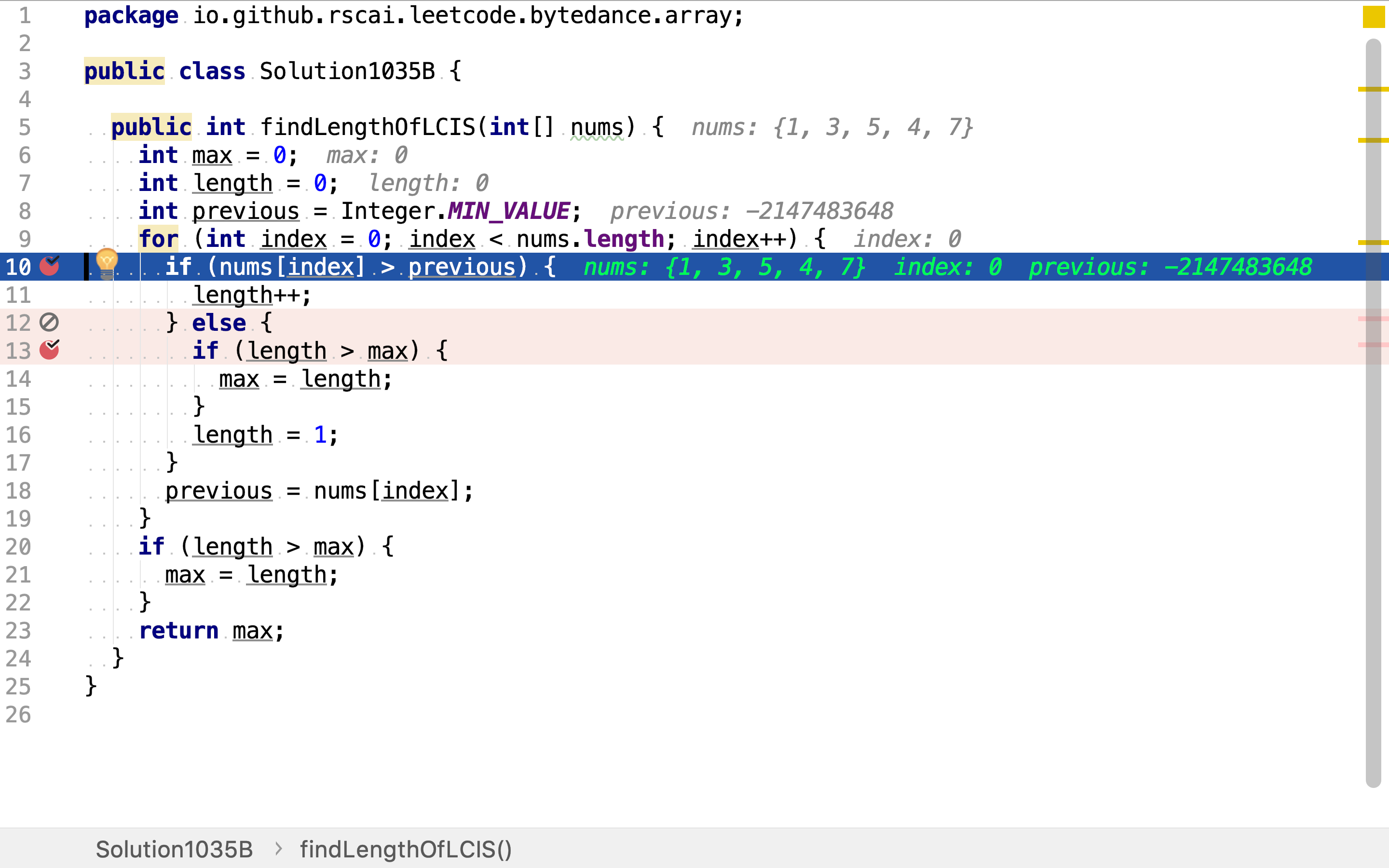
找到第一个连续递增子序列后，以「尾」部元素后一个元素为第二个连续递增子序的「头」，继续寻找下一个连续子序列。同时，先检测已找到的连续递增子序列是否为当前最长。

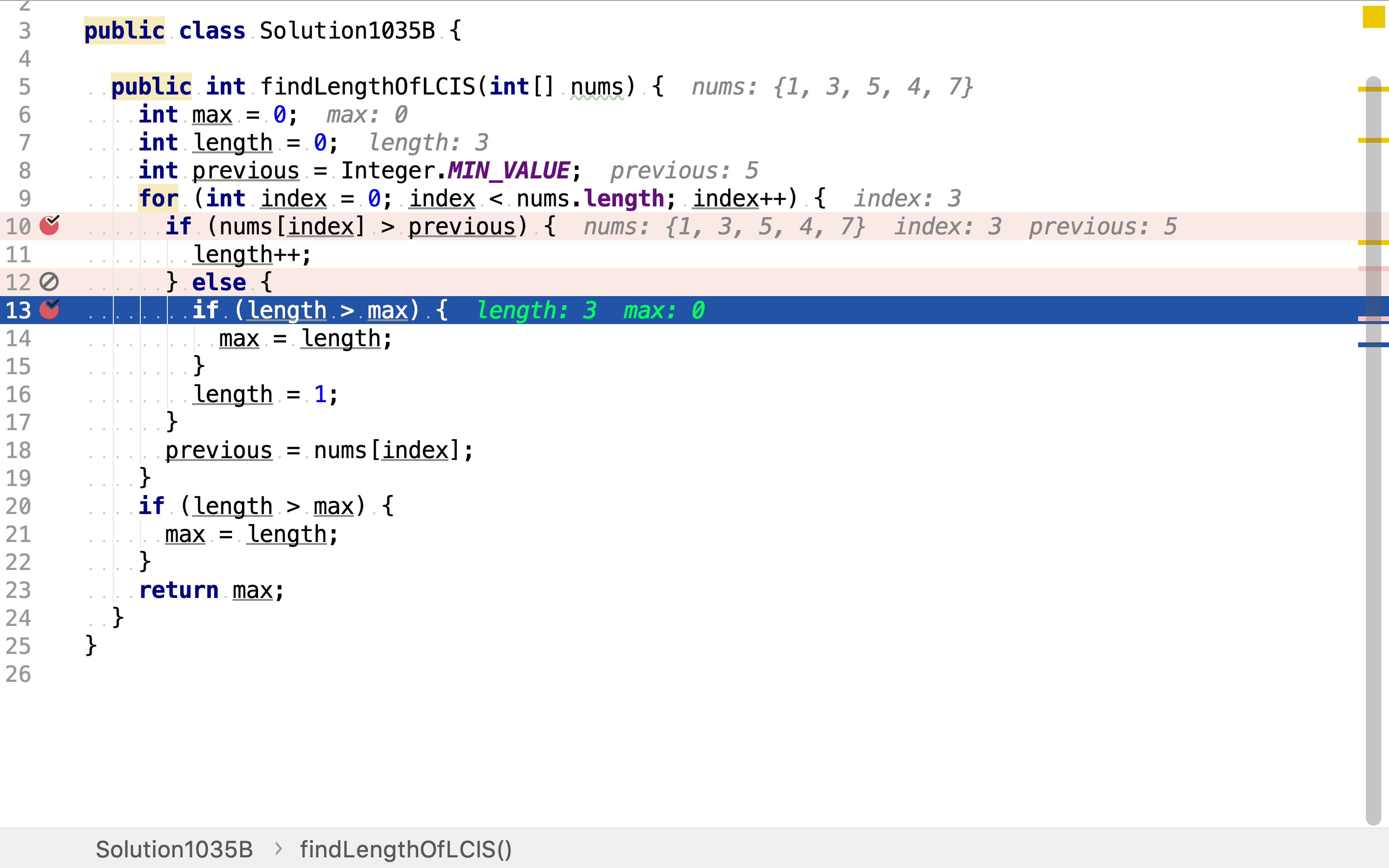
复杂度分析

时间复杂度

祇遍历了一遍数组，时间复杂度为$\mathcal{O}(n)$。

空间复杂度

使用了三个变量max, length, previous，空间复杂度为$\mathcal{O}(1)$。

参考

• 贪婪演算法