俄罗斯套娃信封问题
题目
给定一些标记了宽度和高度的信封,宽度和高度以整数对形式 (w, h) 出现。当另一个信封的宽度和高度都比这个信封大的时候,这个信封就可以放进另一个信封里,如同俄罗斯套娃一样。
请计算最多能有多少个信封能组成一组“俄罗斯套娃”信封(即可以把一个信封放到另一个信封里面)。
说明:
不允许旋转信封。
示例:
输入: envelopes = [[5,4],[6,4],[6,7],[2,3]]
输出: 3
解释: 最多信封的个数为 3, 组合为: [2,3] => [5,4] => [6,7]。
穷举法
给定个信封,分别取个信封排列。再过泸可以嵌套的信封排列。最后取其中嵌套信封最多的排列。
在个元素中取个元素组合排列的数量为。
举个例子,给定四个信封[[5,4],[6,4],[6,7],[2,3]]。套娃信封可以是由一个信封、两个信封、三个信封或四个信封组成。逐一罗列从四个信封中取出一个、两个、三个和四个信封的排列。
从四个信封中取出一个信封有四种排列:
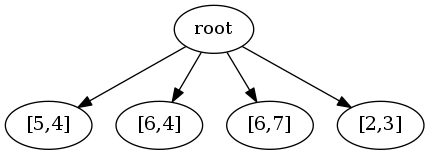
从四个信封中取出两个信封有十二种排列:

代码
package io.github.rscai.leetcode.bytedance.dynamic;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class Solution1031A {
public int maxEnvelopes(int[][] envelopes) {
int envelopeCount = envelopes.length;
int max =0;
List<int[]> envelopeInList = new ArrayList<>(envelopeCount);
for (int index = 0; index < envelopeCount; index++) {
envelopeInList.add(envelopes[index]);
}
for (int n = 1; n <= envelopeCount; n++) {
for (List<int[]> permutation : permute(envelopeInList, n)) {
if (isValid(permutation) && permutation.size() > max) {
max = permutation.size();
}
}
}
return max;
}
private List<List<int[]>> permute(List<int[]> elements, int n) {
List<List<int[]>> permutations = new ArrayList<>();
if (n == 0) {
permutations.add(Collections.emptyList());
}
for (int index = 0; index < elements.size(); index++) {
int[] firstElement = elements.get(index);
List<int[]> remainElements = new ArrayList<>();
remainElements.addAll(elements.subList(0, index));
remainElements.addAll(elements.subList(index + 1, elements.size()));
for (List<int[]> remainPermutation : permute(remainElements, n - 1)) {
List<int[]> permutation = new ArrayList<>();
permutation.add(firstElement);
permutation.addAll(remainPermutation);
permutations.add(permutation);
}
}
return permutations;
}
private boolean isValid(List<int[]> permutation) {
if (permutation.size() == 1) {
return true;
}
int[] outter = permutation.get(0);
for (int index = 1; index < permutation.size(); index++) {
int[] inner = permutation.get(index);
if (inner[0] >= outter[0] || inner[1] >= outter[1]) {
return false;
}
outter = inner;
}
return true;
}
}
首先,依次罗列所有的排列。
然后,过泸出可以嵌套在一起的排列,并求出其中信封数最大值。
排列用递归的方式实现。先将问题拆分为一个「简单的子问题」- 从可选集合𥚃取一个元素。当可选集合大于1时,「一个元素」有多种取值。
除去一个「简单的子问题」后,剩余一个更小的可选元素集合和更小的排列数。
再递归调用自身解决「其余问题」。
递归终止条件为为空。
复杂度分析
时间复杂度
在个元素中取个元素组合排列的数量为。本演算法罗列了从1到m的所有排列。所以,时间复杂度为:
空间复杂度
其罗列了所有的排列,空间复杂度为:
贪婪法
贪婪演算法(英语:greedy algorithm),又称贪心演算法,是一种在每一步选择中都採取在目前状态下最好或最佳(即最有利)的选择,从而希望导致结果是最好或最佳的演算法。
假设给定一个信封a,在选择一个信封放入a中时,选择了可容维信封数最多的信封,则将其放入a所组成的「套娃信封」数是最大。
递推公式:
其中,是以为最外层信封组成的「套娃信封」最大数,为能容纳的所有信封集合。
代码
package io.github.rscai.leetcode.bytedance.dynamic;
import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.List;
public class Solution1031B {
public int maxEnvelopes(int[][] envelopes) {
List<int[]> envelopeInList = new ArrayList<>(envelopes.length);
for (int[] envelope : envelopes) {
envelopeInList.add(envelope);
}
Collections.sort(envelopeInList, new Comparator<int[]>() {
@Override
public int compare(int[] left, int[] right) {
if (left[0] < right[0]) {
return -1;
} else if (left[0] > right[0]) {
return 1;
} else {
if (left[1] < right[1]) {
return -1;
} else if (left[1] > right[1]) {
return 1;
} else {
return 0;
}
}
}
});
int[] maxs = new int[envelopeInList.size()];
for (int index = 0; index < envelopeInList.size(); index++) {
int[] envelope = envelopeInList.get(index);
int canHoldMax = 0;
for (int k = index - 1; k >= 0; k--) {
int[] inner = envelopeInList.get(k);
if (envelope[0] > inner[0] && envelope[1] > inner[1] && maxs[k] > canHoldMax) {
canHoldMax = maxs[k];
}
}
maxs[index] = canHoldMax + 1;
}
int max = 0;
for (int value : maxs) {
if (value > max) {
max = value;
}
}
return max;
}
}
首先,将信封从小到大排序。因为信封的「尺寸」是一个二维向量,所以实际上无法以一维排序。这𥚃按一个近似的序列排序:先比较长,若长相等则比较寛。
然后,从小往大依次计算以每个信封为最外层信封所能组成的最大「套娃信封」。
一个信封所能组成的最大「套娃信封」由其所能容纳的所有信封中「套娃信封」值最大的再加1。因为所有信封都从小到大排序了(虽然是㧒近似的顺序排序的,但保证了右侧的信封绝不会小于左侧信封),所以「可容纳的信封」都在序列左侧。
最后,再遍历一遍,找出最大的「套娃信封」。
复杂度分析
时间复杂度
本演算法使用一次JDK中ArrayList的排序实现,其时间复杂度是。再两层循环遍历所有信封。时间复杂度为:
空间复杂度
使用了尺寸与轮入值相同的maxs存储子问题解。空间复杂度为:











