第k个排列
题目
给出集合
[1,2,3,…,n],其所有元素共有n!种排列。按大小顺序列出所有排列情况,并一一标记,当
n = 3时, 所有排列如下:
"123""132""213""231""312""321"给定
n和k,返回第k个排列。说明:
给定
n的范围是[1,9]。给定
k的范围是[1,n!]。
非固定进制法
我们可以将按大小顺序列出的所有排序视为非固定进制的整数。固定进制的整数,比如十进制整数,
- 每一位都在
0, 1, 2, 3, 4, 5, 6, 7, 8, 9之中循环 - 假设位数为,第个十进制整数中,第一位(从左往右数)的值为,第(,从0开始计)位止值为
排列的特点是,每一位的取值范围是不同的。假设是个元素排列,第一位的取值范围是个,第二位的取值范围是个,第三位的取值范围是,依此类推。
所以,将个元素所有排序按大小顺序列出,第个排序中,第位的值为。
代码实现
首先,按着公式计算每一位值的索引。
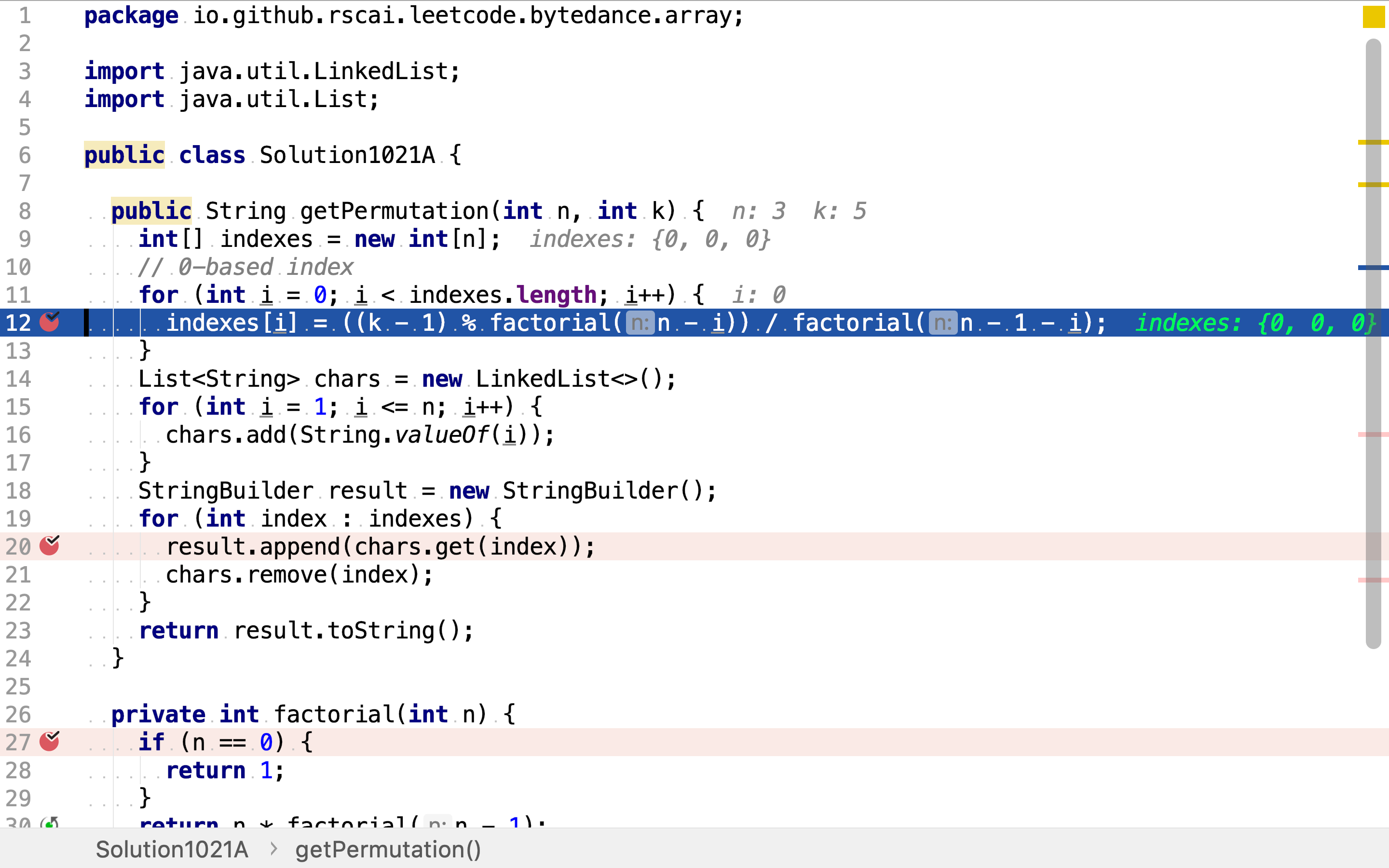
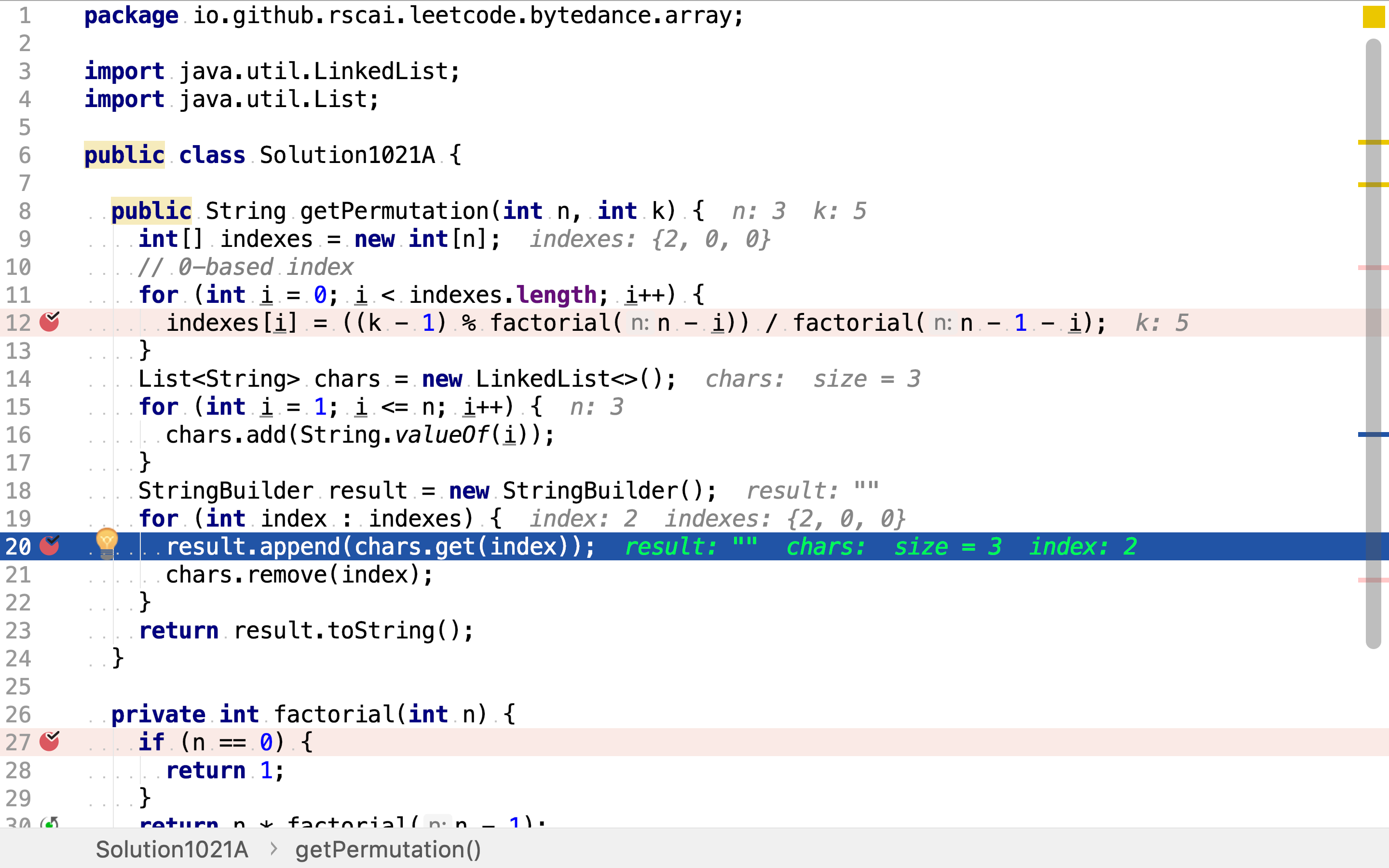
然后,获取每一位上的值。因为每一位上的候选值列表都不相同,而且受前面位上取值影响。所以,每决定一位的值,都要将其从候选列表中移除。
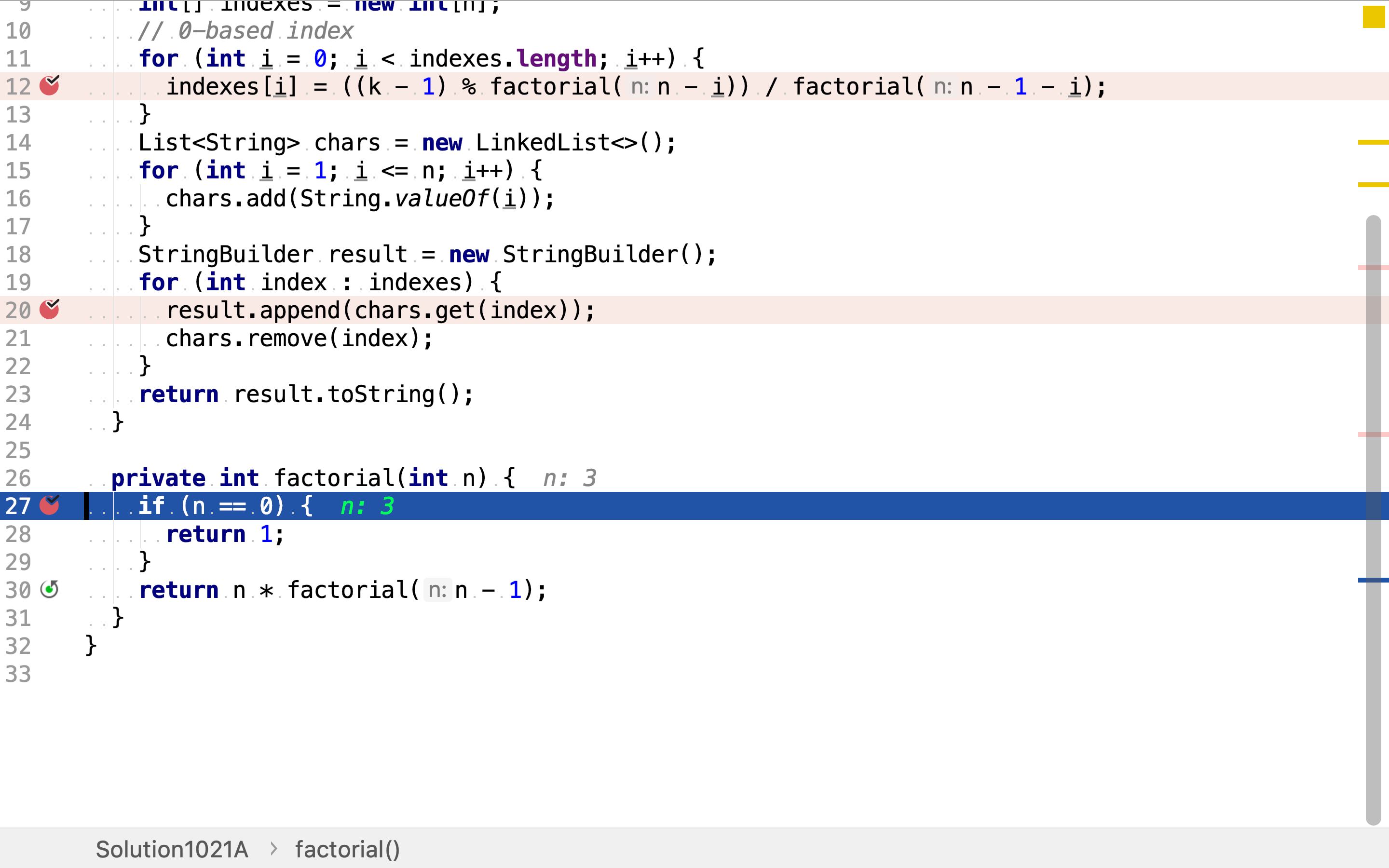
阶乘则以递归实现。
复杂度分析
时间复杂度
本演算法针对每一位都计算了两次阶乘。然后,遍历了每一位两次。时间复杂度为:
空间复杂度
使用了三个长度为的列表。空间复杂度为:
动态规划法
上述演算法时间复杂度发生在计算阶乘。阶乘是以递归实现的,将阶乘的递归以树的形式展现:
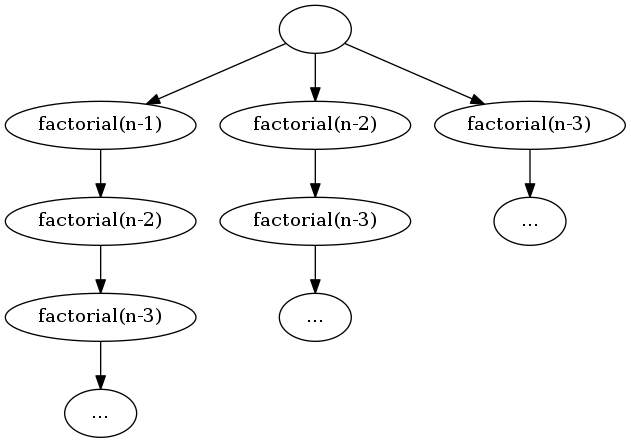
可以发现有很多子树是重复的,这意味着「有重复的子问题」,以以使用「动态规划」优化。
动态规划
动态规划(英语:Dynamic programming,简称DP)是一种在数学、管理科学、电脑科学、经济学和生物资讯学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
动态规划常常适用于有重叠子问题和最佳子结构性质的问题,动态规划方法所耗时间往往远少于朴素解法。
动态规划背后的基本思想非常简单。大致上,若要解一个给定问题,我们需要解其不同部分(即子问题),再根据子问题的解以得出原问题的解。
通常许多子问题非常相似,为此动态规划法试图仅仅解决每个子问题一次,从而减少计算量:一旦某个给定子问题的解已经算出,则将其记忆化储存,以便下次需要同一个子问题解之时直接查表。这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。
概述
动态规划在寻找有很多重叠子问题的情况的最佳解时有效。它将问题重新组合成子问题。为了避免多次解决这些子问题,它们的结果都逐渐被计算并被储存,从简单的问题直到整个问题都被解决。因此,动态规划储存递回时的结果,因而不会在解决同样的问题时花费时间。
动态规划只能应用于有最佳子结构的问题。最佳子结构的意思是局部最佳解能决定全域最佳解(对有些问题这个要求并不能完全满足,故有时需要引入一定的近似)。简单地说,问题能够分解成子问题来解决。
适用情况
- 最佳子结构性质。如果问题的最佳解所包含的子问题的解也是最佳的,我们就称该问题具有最佳子结构性质(即满足最佳化原理)。最佳子结构性质为动态规划演算法解决问题提供了重要线索。
- 无后效性。即子问题的解一旦确定,就不再改变,不受在这之后、包含它的更大的问题的求解决策影响。
- 子问题重叠性质。子问题重叠性质是指在用递回演算法自顶向下对问题进行求解时,每次产生的子问题并不总是新问题,有些子问题会被重复计算多次。动态规划演算法正是利用了这种子问题的重叠性质,对每一个子问题只计算一次,然后将其计算结果储存在一个表格中,当再次需要计算已经计算过的子问题时,只是在表格中简单地检视一下结果,从而获得较高的效率。
参考
代码实现
首先,一样地按着公式计算每一位值的索引。
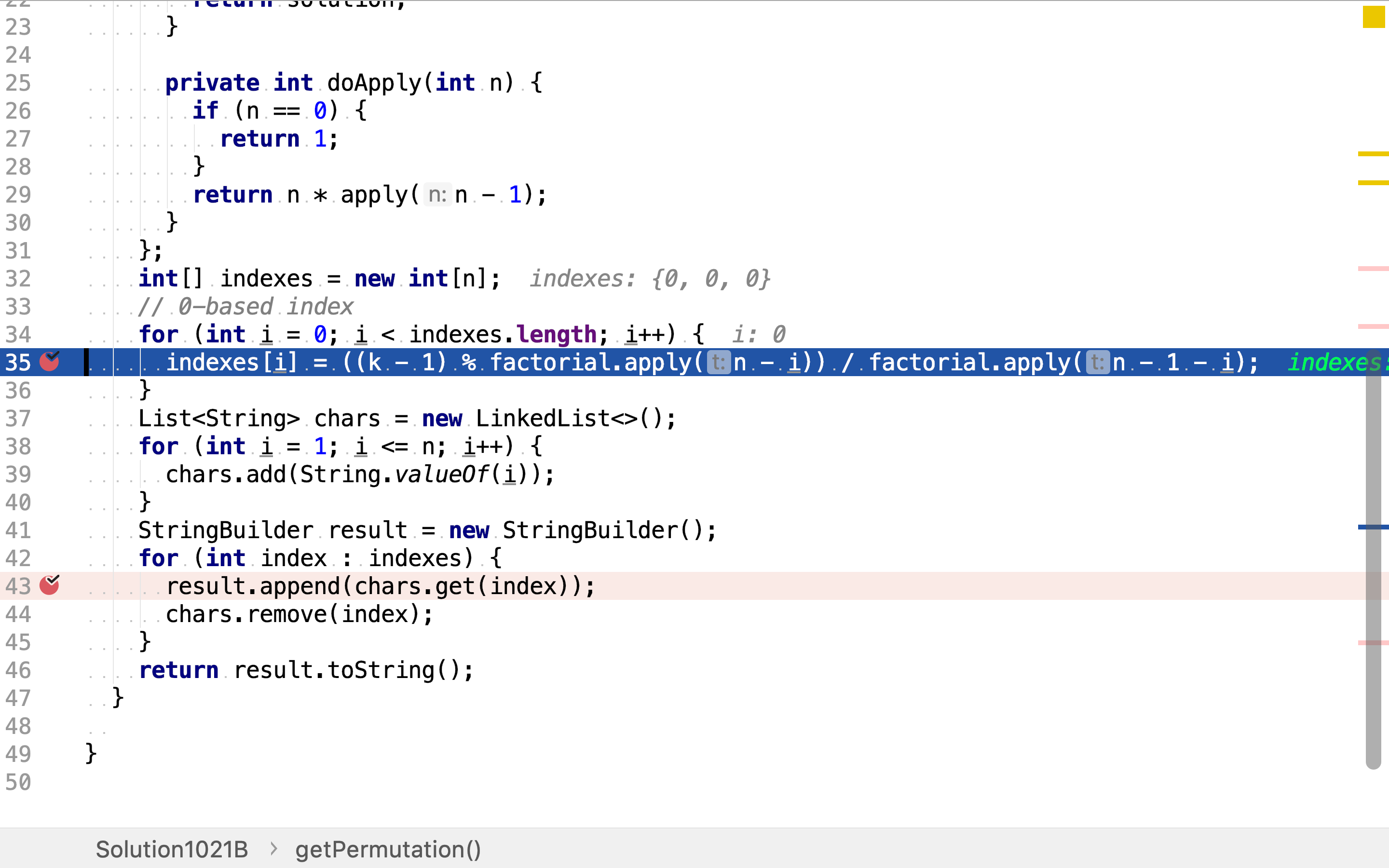
然后,获取每一位上的值。因为每一位上的候选值列表都不相同,而且受前面位上取值影响。所以,每决定一位的值,都要将其从候选列表中移除。
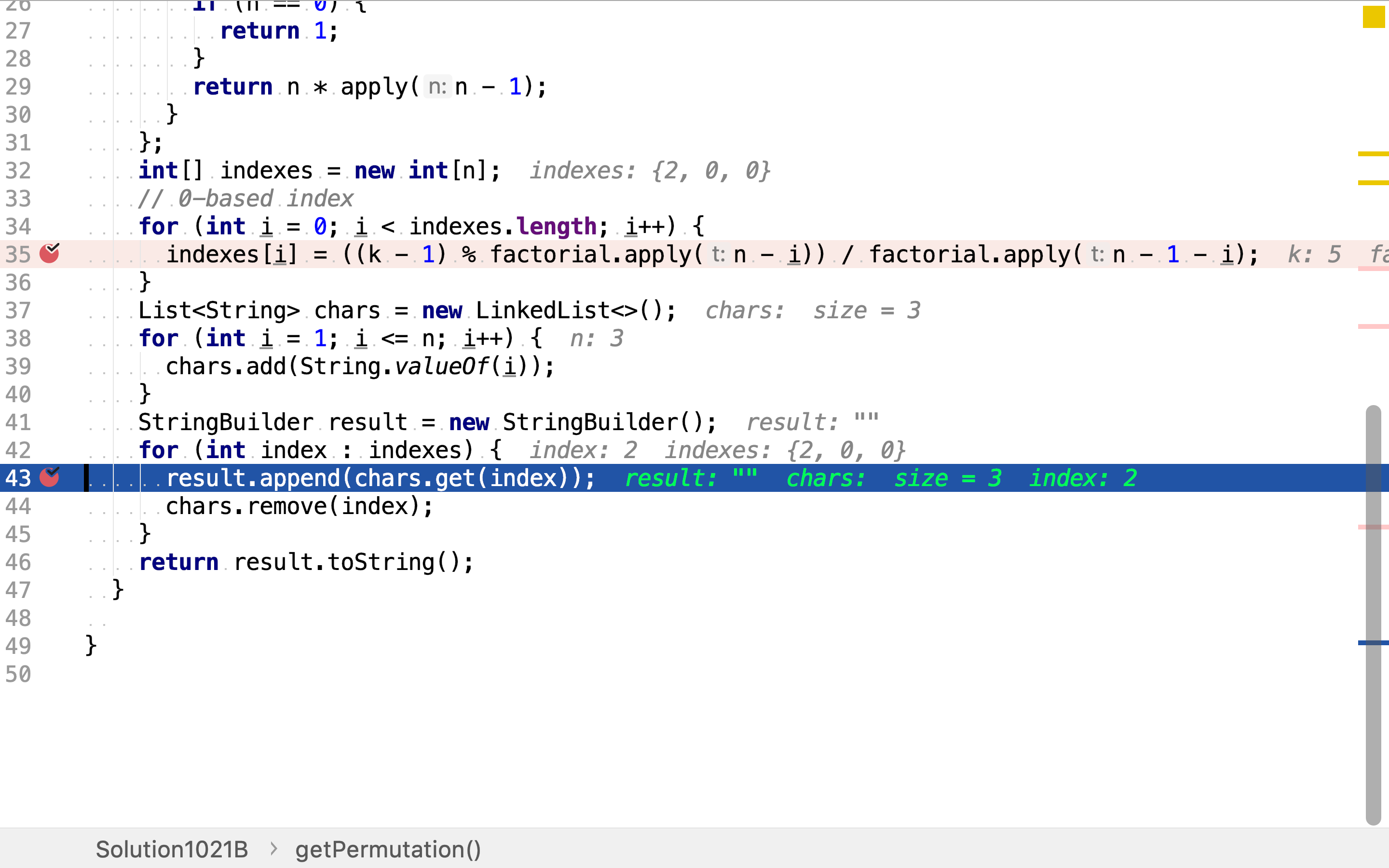
阶乘使用函数式实现,该函数使用HashMap存储函数值,从而实现「动态规划」避免重复计算。
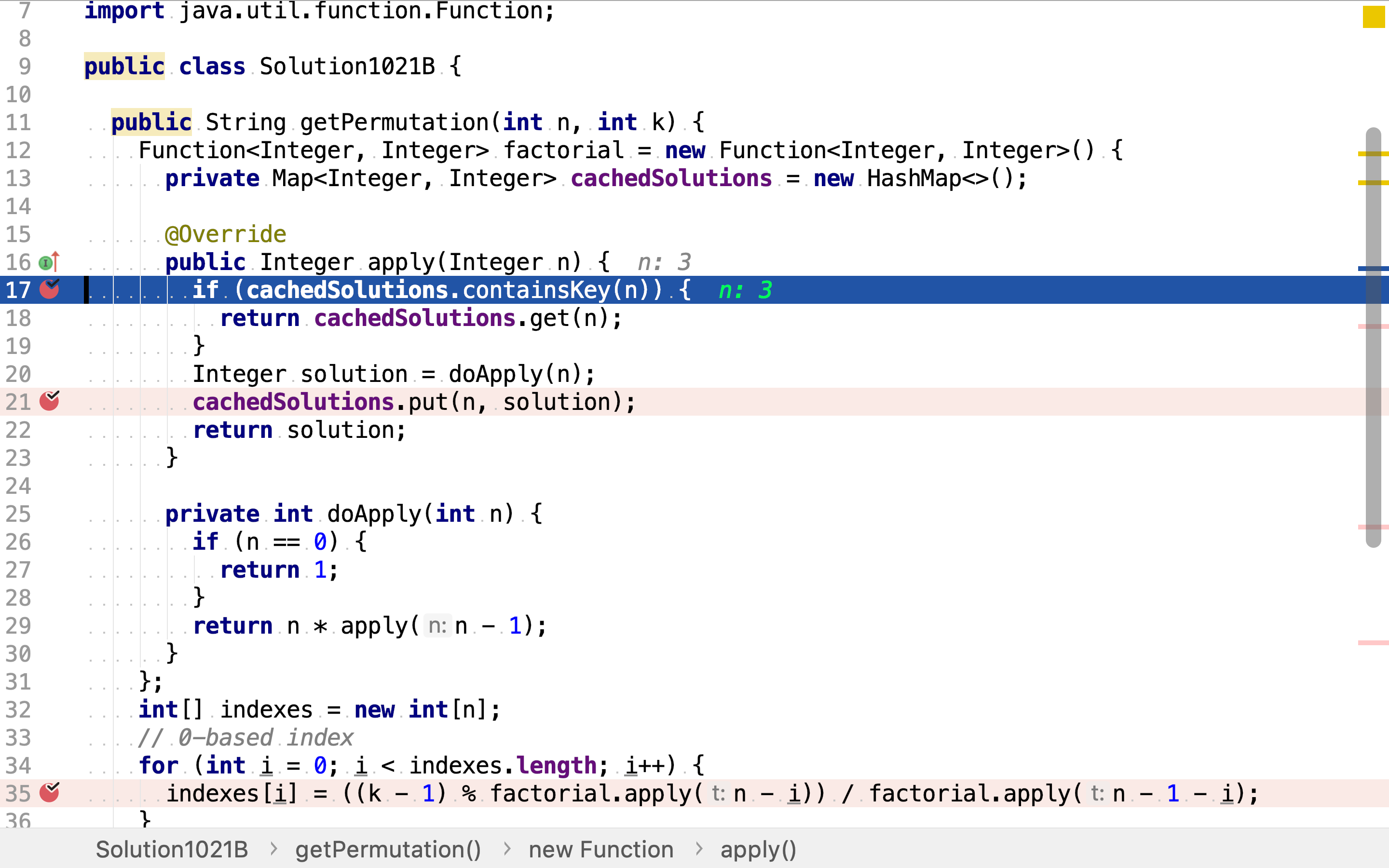
复杂度分析
时间复杂度
因为存储了阶乘函数的值,所以其实际祇执行了次乘。所以时间复杂度优化至。
空间复杂度
其最多存储了个函数值,所以空间复杂度依旧是。
一次遍历法
将上述演算法中所执行的阶乘以树的形式展现:

以深度优先从右往左后序遍历树(相当于从右往左依次按公式计算每第个排列上的每一位),得到factorial执行序列..., factorial(n-3), ..., factorial(n-3), factorial(n-2), ..., factorial(n-3), factorial(n-2), factorial(n-1),去掉重复得到..., factorial(n-3), factorial(n-2), factorial(n-1)。再从阶乘的定义可推。所以,当从右往左依次按公式计算每第个排列上的每一位时,祇需要保存之前两个factorial函数的值。
代码实现
通过公式可知计算第个排列中每一位的值都需要两个factorial的值,所以就建立两个变量去保存这两个factorial值。
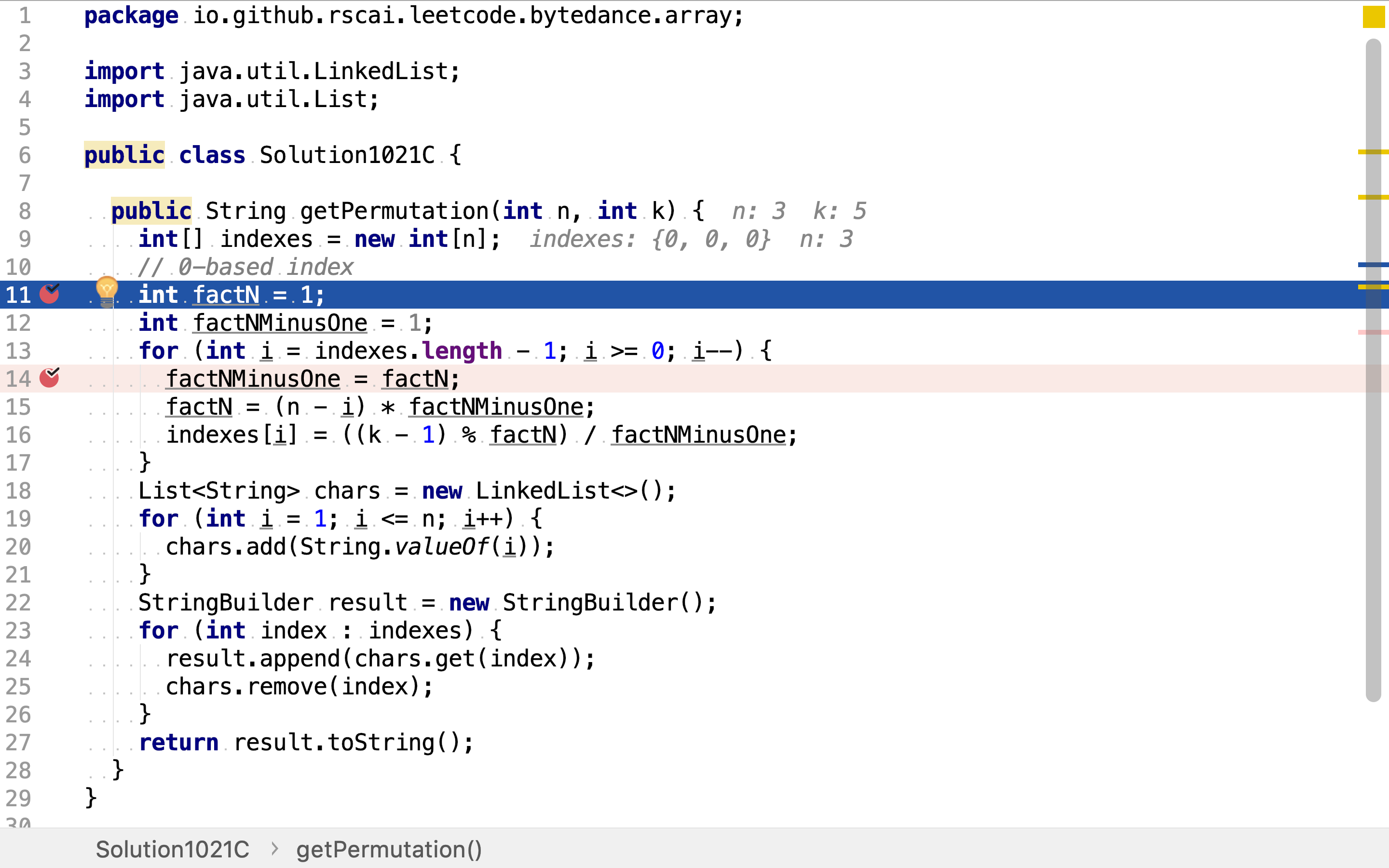
计算每一位时都需要两个factorial值,需每一个factorial值计算都需要前一个factorial值。比如,计算第位时,需计算factorial(n-1-i)和factorial(n-i),计算factorial(n-1-i)和factorial(n-i)时又分别需要计算factorial(n-1-i-1)和factorial(n-i-1)。其中factorial(n-1-i-1)和factorial(n-i-1)的值在计算后一位(从右往左计算每一位的值)值时已得到并保存,所以此轮无需重复计算。
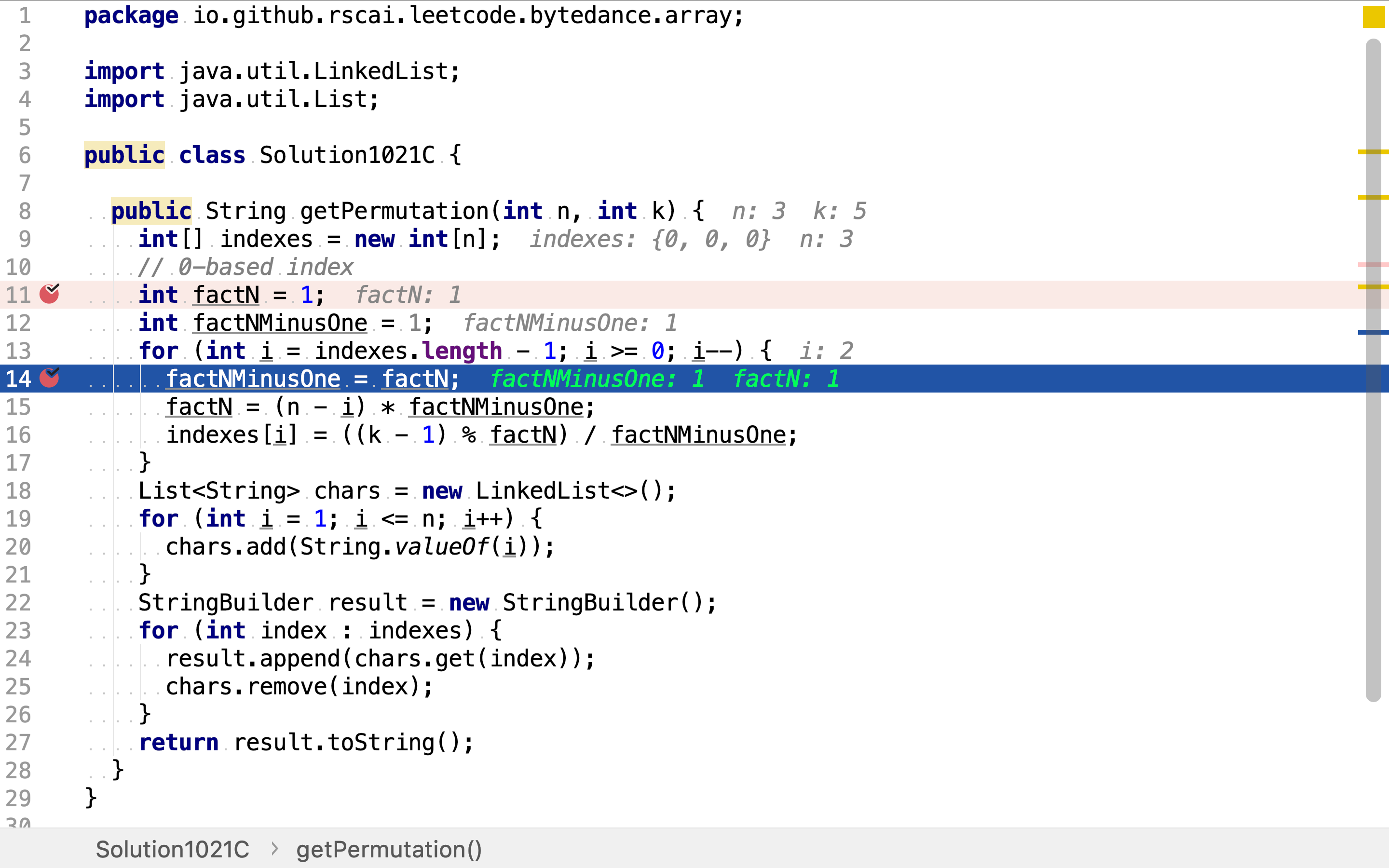
复杂度分析
时间复杂度
时间复杂度与「动态规划法」相同,。
空间复杂度
相较与「动态规划法」,本演算法祇保存了两个factorial的值,在计算阶乘环节其空间复杂度为。但其它部份的空间复杂度并没有降低,所以总体空间复杂度依旧为。