接雨水
题目
给定n个非负整数表示每个宽度为1的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
上面是由数组[0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接6 个单位的雨水(蓝色部分表示雨水)。感谢 Marcos 贡献此图。
示例:
输入: [0,1,0,2,1,0,1,3,2,1,2,1] 输出: 6
暴力法
对于每一根柱子,其上雨水可达的最大高度为其左右两边最高柱子中较低的一根柱子的高度,再减去柱子本身的高度即为两水的深度。
举个例子,给定如下柱图:
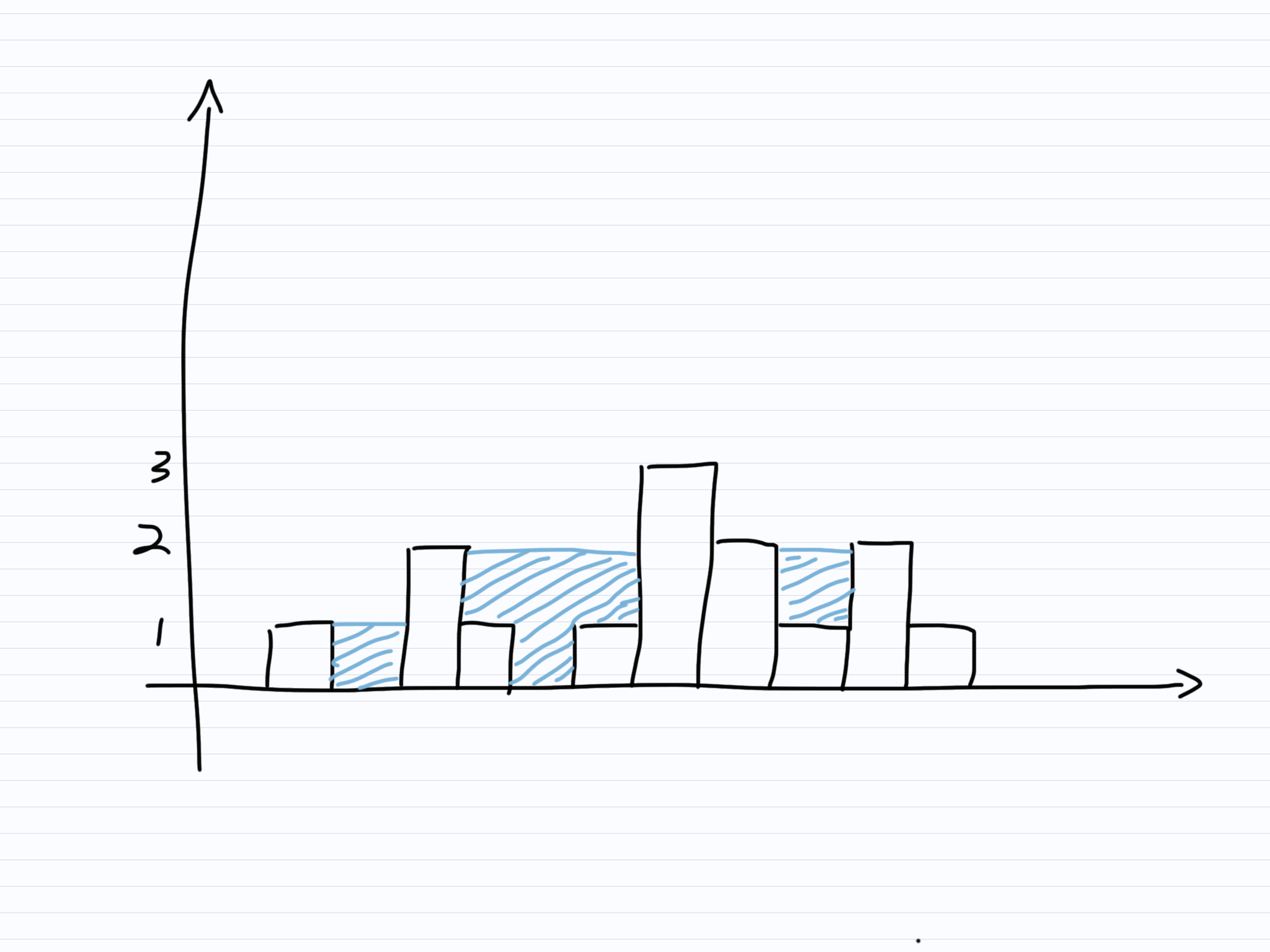
第1根柱子左边中最高的柱子高度为0,右边最高柱子高度为3,则其积水最大可达高度0。
第二根柱子左边最高柱子高度为1,右边最高柱子高度为3,则其积水最大可达高度1。再减去柱子本身高度0,则积水深度最大可达1。
第三根柱子左边最高柱子高度为1,右边最高柱子高度为3,则其积水最大可达高度为1。但其自身高度为2,则积水深度最大为0。
第四根柱子左边最高柱子高度为2,右边最高柱子高度为3,则其积水最大可达高度为2。减去自身高度1,则积水深度最大为1。
第五根柱子左边最高柱子高度为2,右边最高柱子高度为3,则其积水最大高度为2。减去自身高度0,积水最大深度为2。
。。。
代码实现
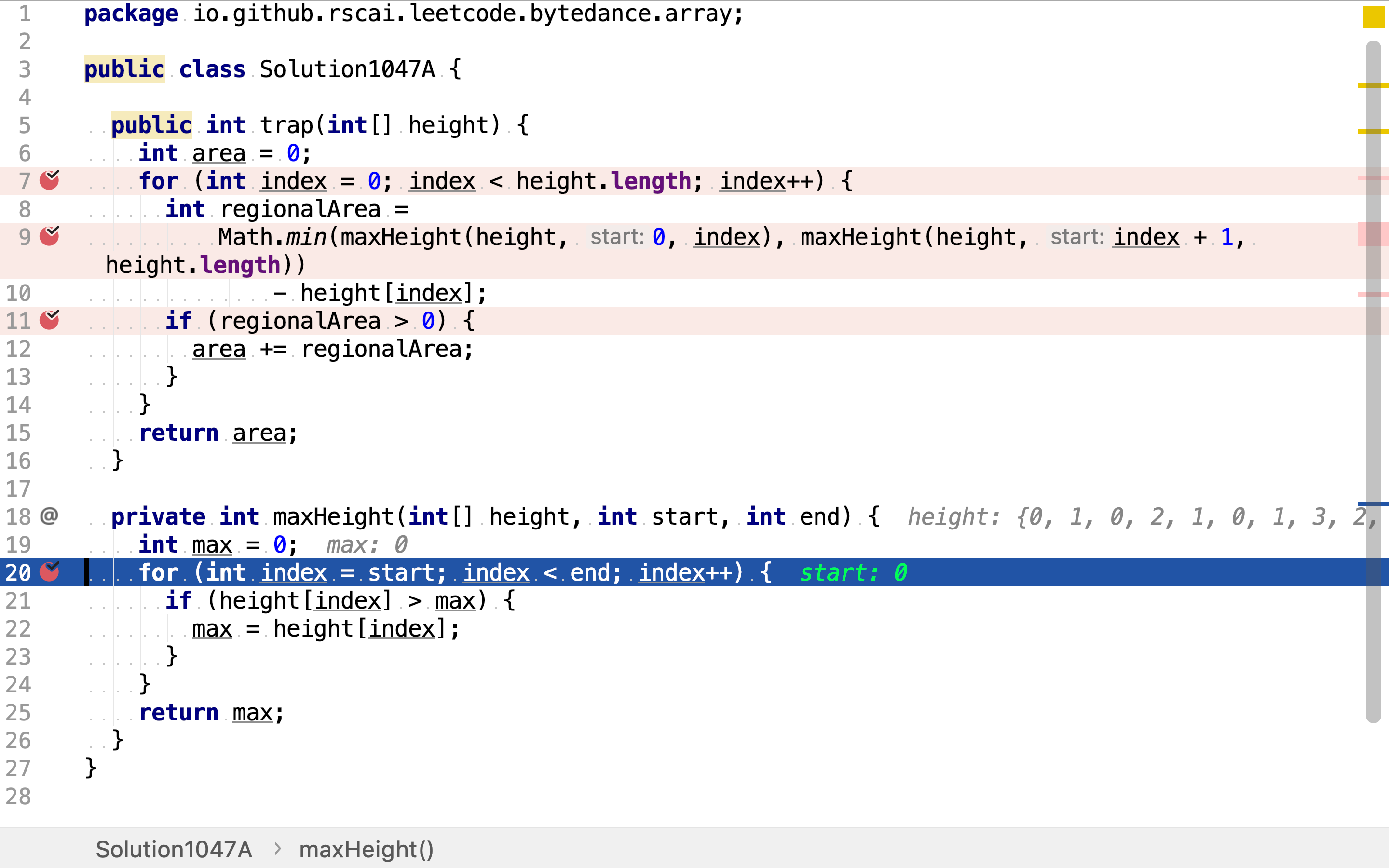
首先,遍历每根柱子。
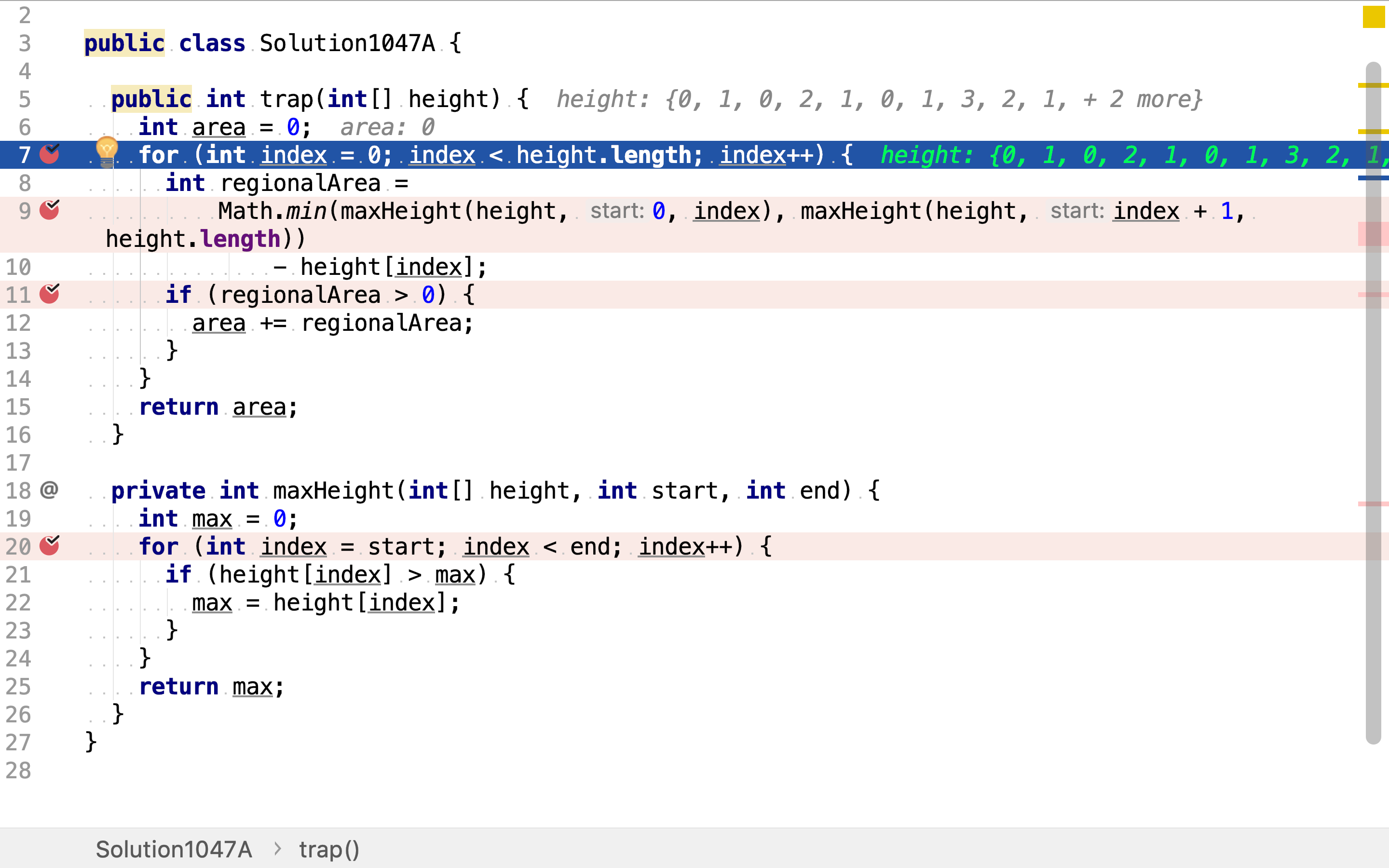
然后,针对每一根柱子,计算其左边最高柱子和右边最高柱子,取其中较低者再减去柱子本身的高度,得到本柱子上方积水的深度。
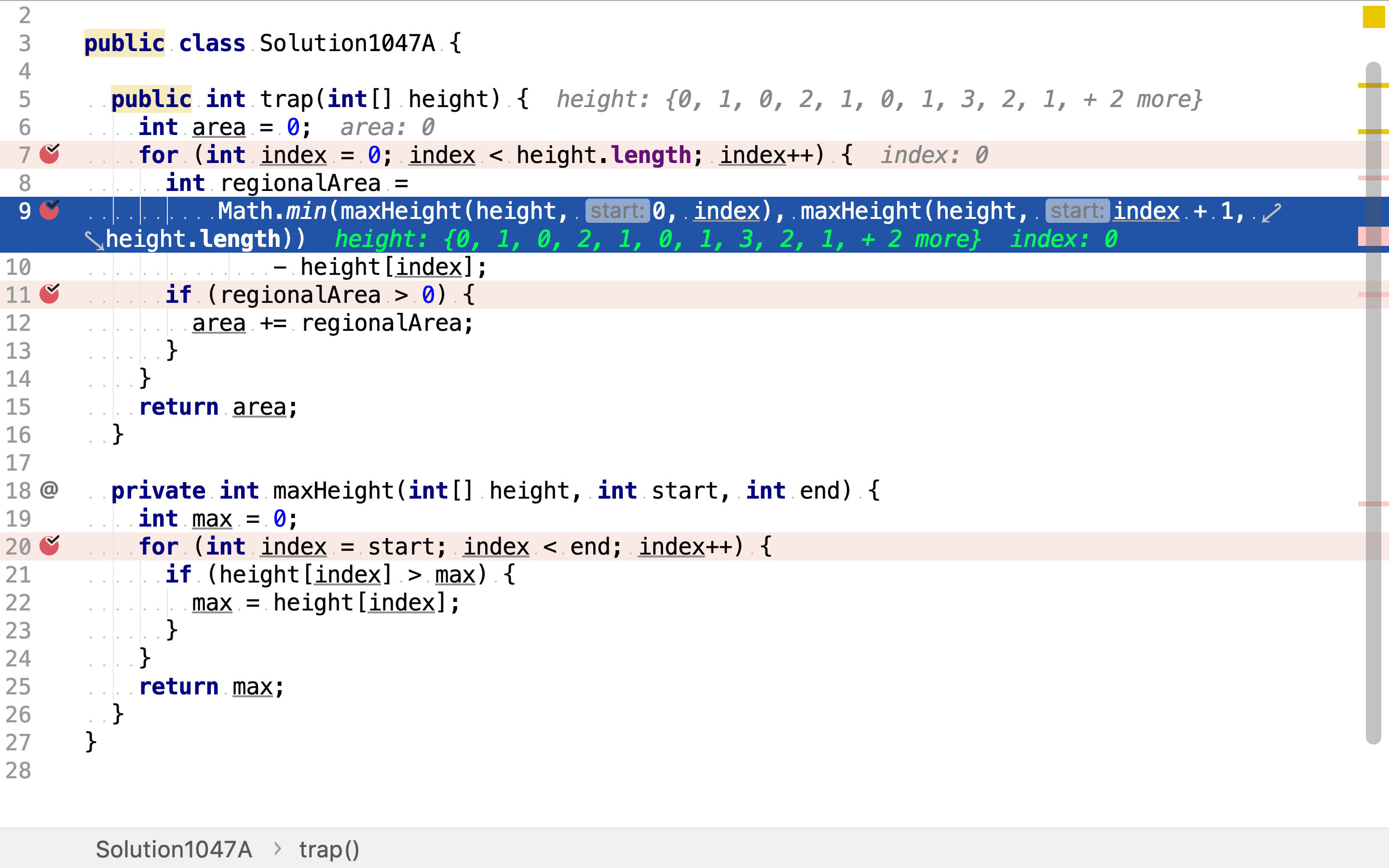
最后,累加积水深度。若积水深度为负数,则等同于0。
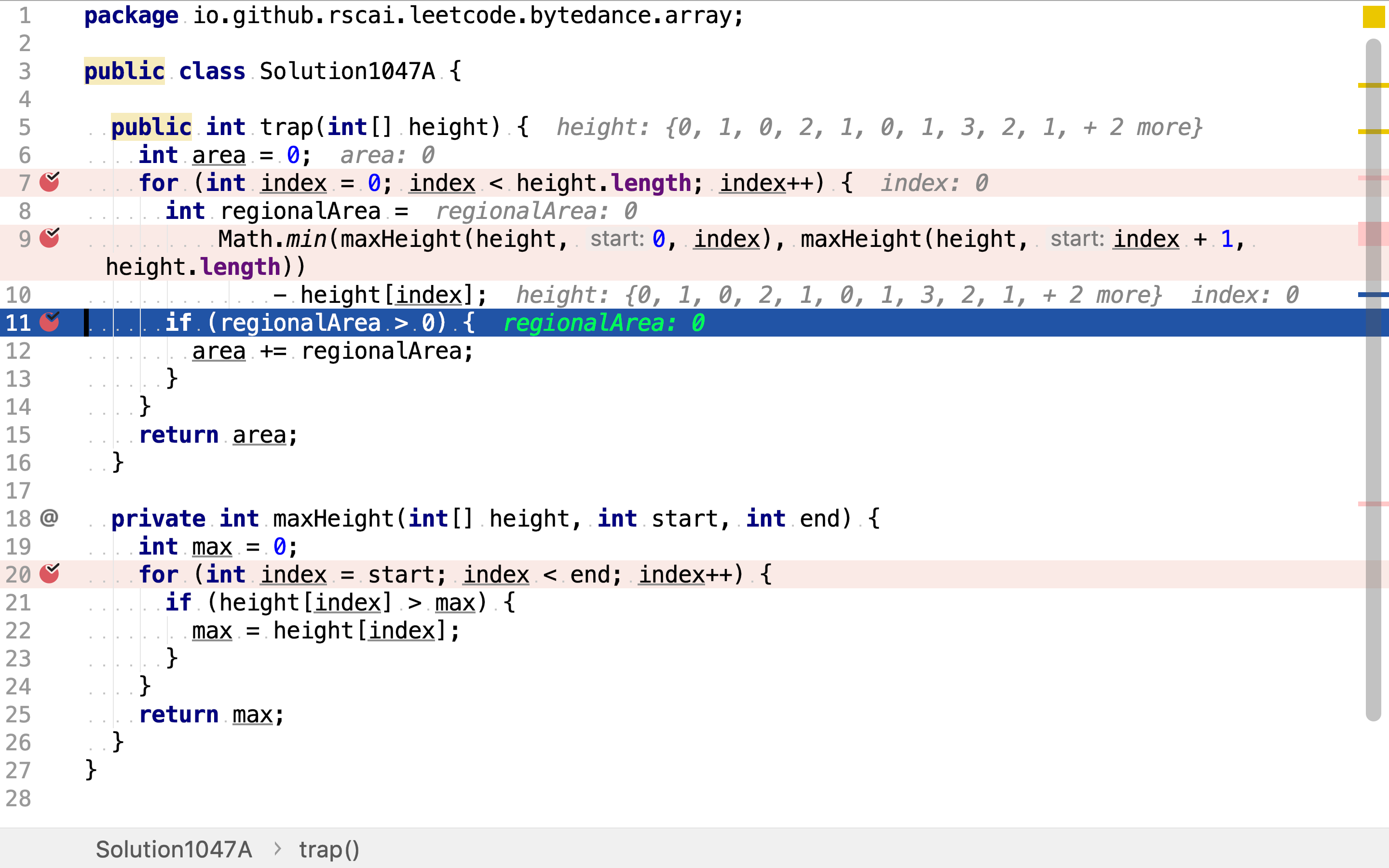
左边和右边的最高柱子由分别遍历左右所有柱子得到。
复杂度分析
时间复杂度
本演算法针对每根柱子都需要通过遍历一遍所有柱子找到左右两边最高的柱子。所以时间复杂度为。
空间复杂度
使用了三个变量area, index, regionalArea,空间复杂度为。
动态规划法
动态规划
动态规划(英语:Dynamic programming,简称DP)是一种在数学、管理科学、电脑科学、经济学和生物资讯学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
动态规划常常适用于有重叠子问题和最佳子结构性质的问题,动态规划方法所耗时间往往远少于朴素解法。
动态规划背后的基本思想非常简单。大致上,若要解一个给定问题,我们需要解其不同部分(即子问题),再根据子问题的解以得出原问题的解。
通常许多子问题非常相似,为此动态规划法试图仅仅解决每个子问题一次,从而减少计算量:一旦某个给定子问题的解已经算出,则将其记忆化储存,以便下次需要同一个子问题解之时直接查表。这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。
概述
动态规划在寻找有很多重叠子问题的情况的最佳解时有效。它将问题重新组合成子问题。为了避免多次解决这些子问题,它们的结果都逐渐被计算并被储存,从简单的问题直到整个问题都被解决。因此,动态规划储存递回时的结果,因而不会在解决同样的问题时花费时间。
动态规划只能应用于有最佳子结构的问题。最佳子结构的意思是局部最佳解能决定全域最佳解(对有些问题这个要求并不能完全满足,故有时需要引入一定的近似)。简单地说,问题能够分解成子问题来解决。
适用情况
- 最佳子结构性质。如果问题的最佳解所包含的子问题的解也是最佳的,我们就称该问题具有最佳子结构性质(即满足最佳化原理)。最佳子结构性质为动态规划演算法解决问题提供了重要线索。
- 无后效性。即子问题的解一旦确定,就不再改变,不受在这之后、包含它的更大的问题的求解决策影响。
- 子问题重叠性质。子问题重叠性质是指在用递回演算法自顶向下对问题进行求解时,每次产生的子问题并不总是新问题,有些子问题会被重复计算多次。动态规划演算法正是利用了这种子问题的重叠性质,对每一个子问题只计算一次,然后将其计算结果储存在一个表格中,当再次需要计算已经计算过的子问题时,只是在表格中简单地检视一下结果,从而获得较高的效率。
参考
柱子跟柱子之间的「左边柱子」和「右边柱子」有部份重叠。这些重叠的部份就是「动态规划」可以优化的地方。
举个例子,给定如下柱图:

第一根柱子上的积水深度由左边最高的柱子和右边最高的柱子决定。而左边柱子为空。右边柱子包括了第2,3,4,5,6,7,8,9,10,11根柱子,其最高的柱子为第2根与其余柱子中最高者之间的较高者。
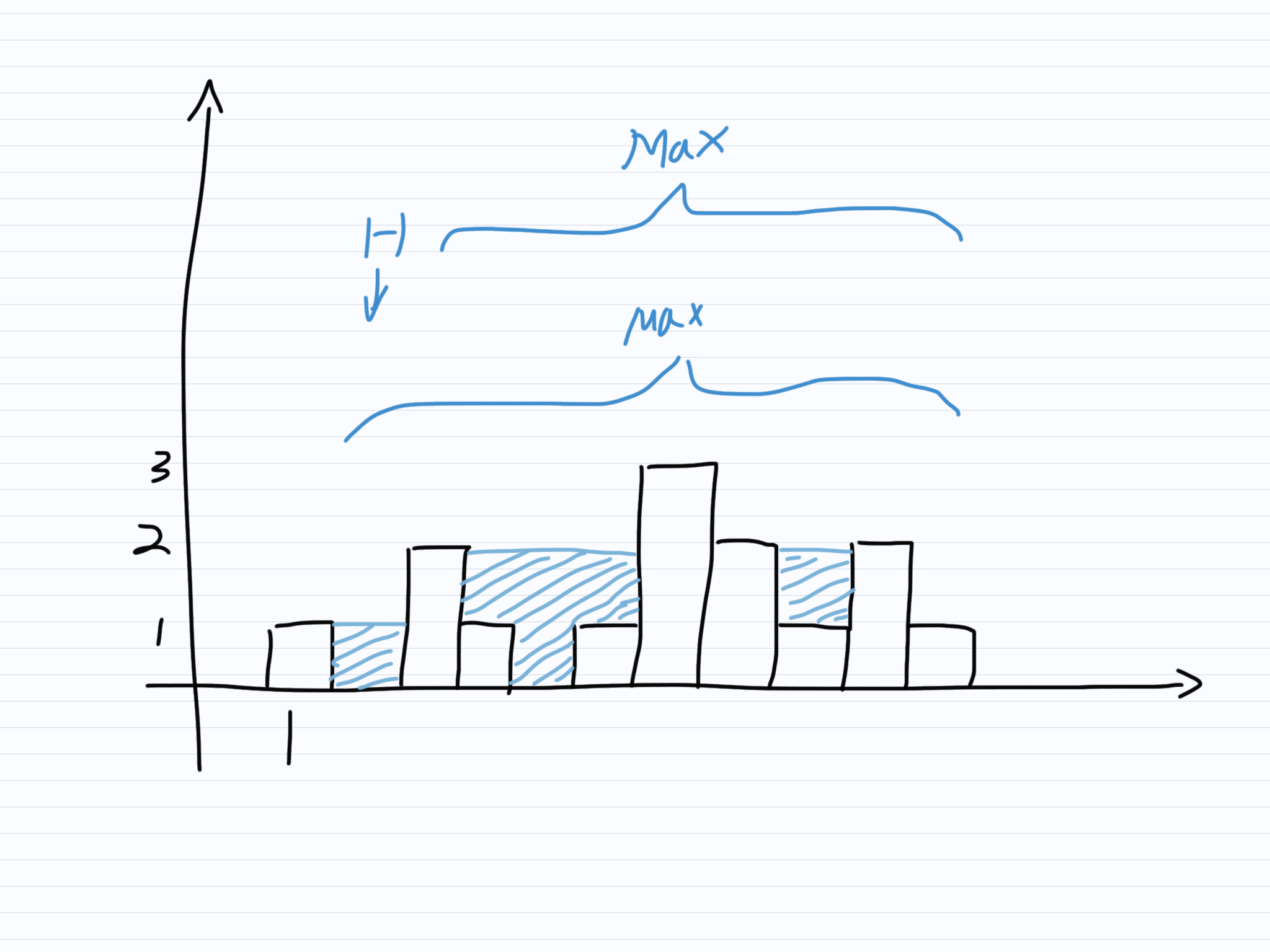
其余柱子中最高者则可运用递归法求得。相似地,第二根柱子上的积水深度由左边最高的柱子和右边最高的柱子决定,而左右两边最高的柱子都可运用递归法求得。
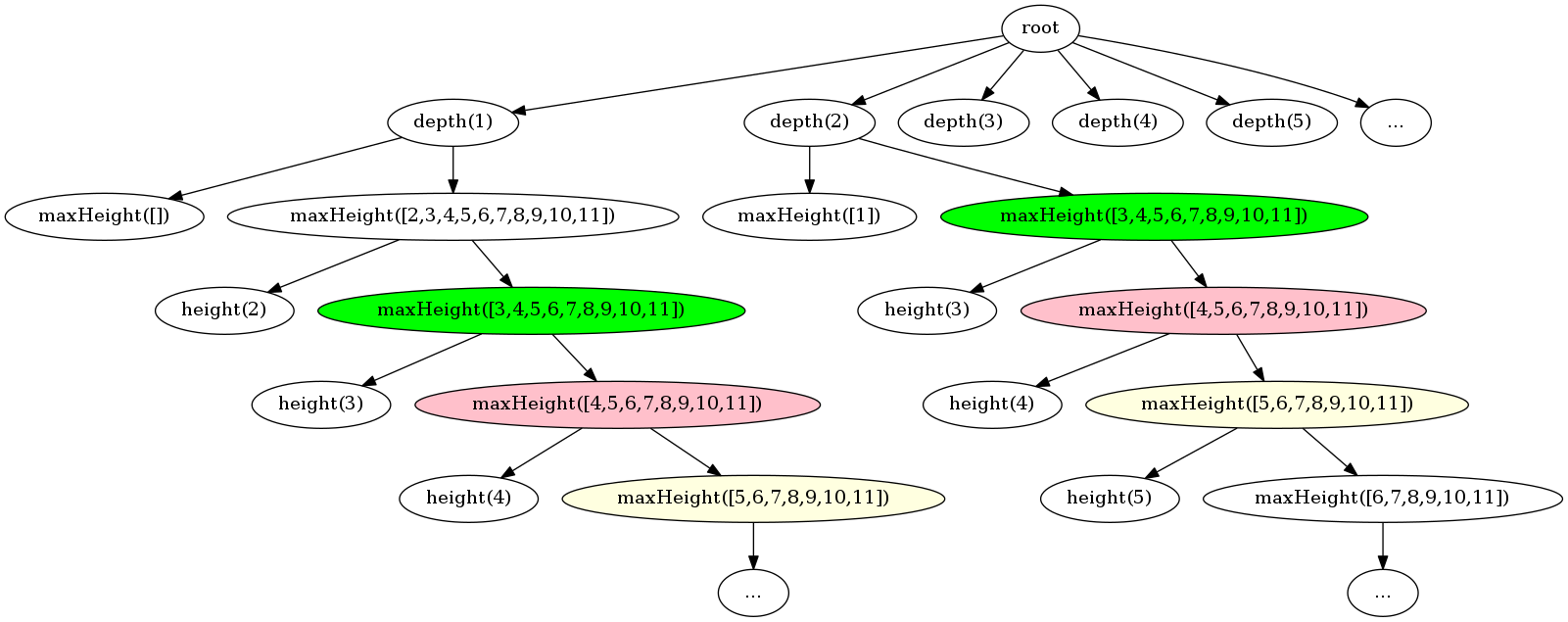
将所有子问题及其子问题以树的形式展现,可以直观地发现很多相同的子树,这些重复的子树就是「重叠的子问题」。将重重叠子问题的解保存以供后续使用,避免重复计算相同的问题,这正是「动态规划」的核心。
代码实现
大体上与暴力法相似,首先遍历每根柱子。
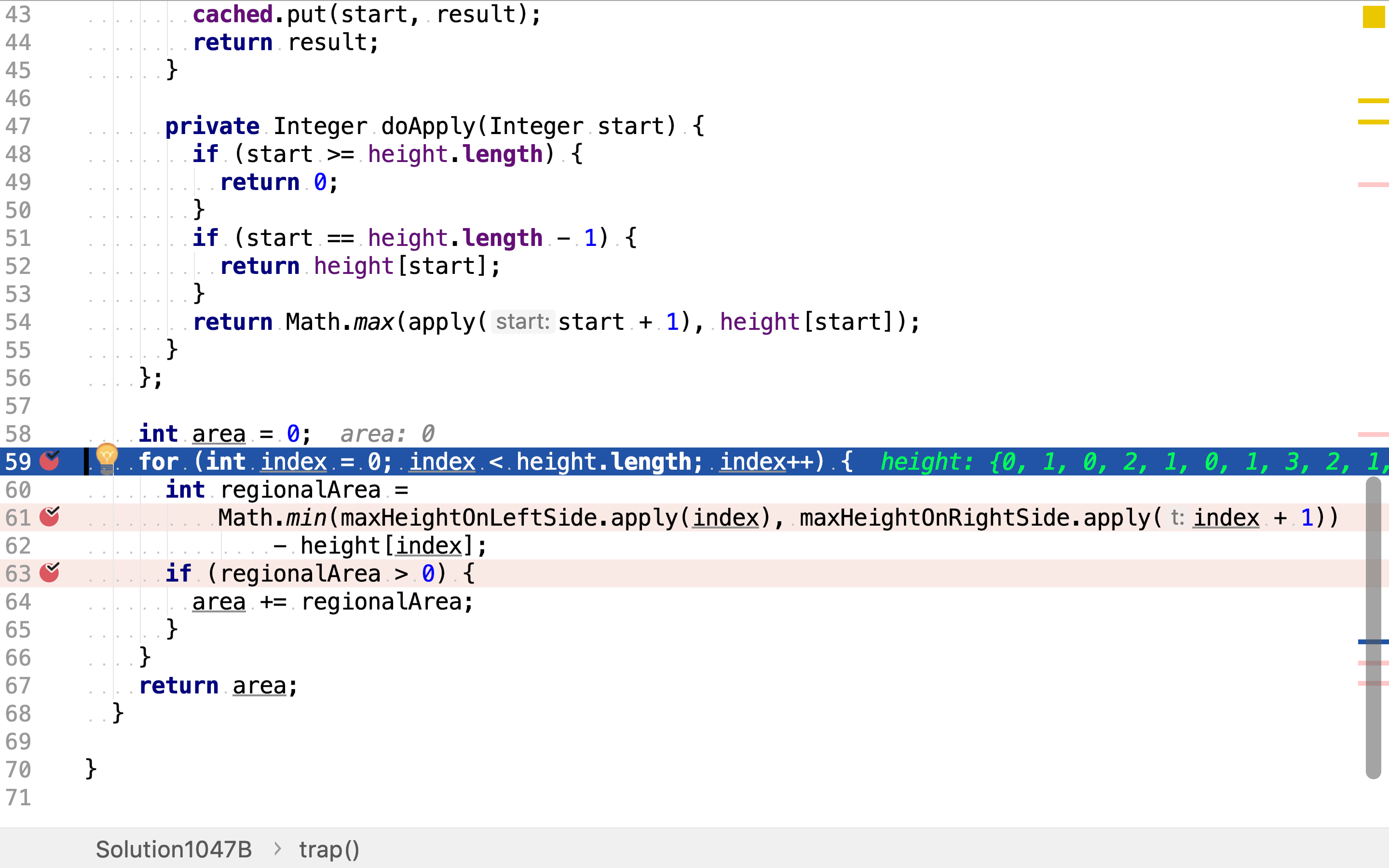
然后,针对每一根柱子,计算其左边最高柱子和右边最高柱子,取其中较低者再减去柱子本身的高度,得到本柱子上方积水的深度。
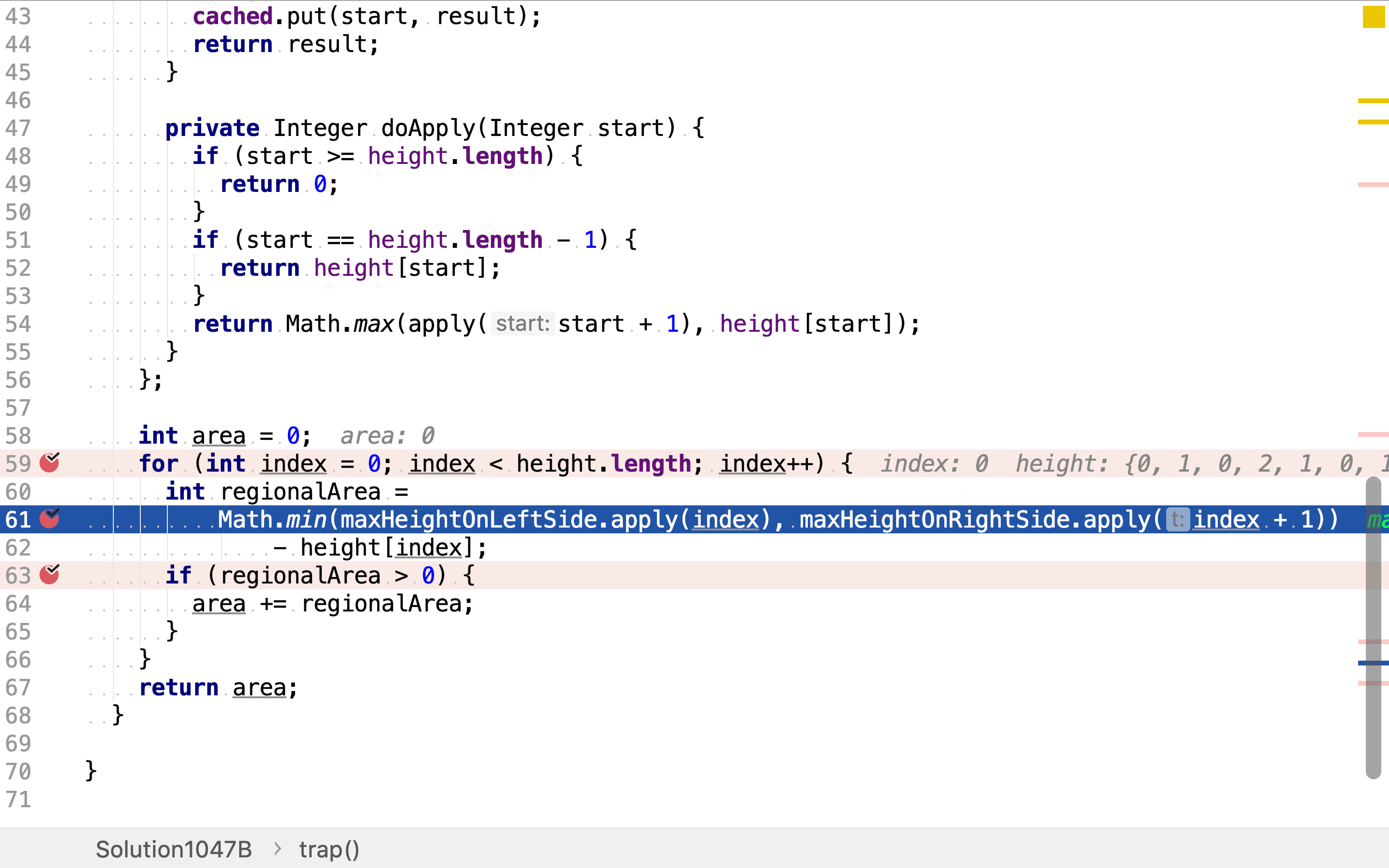
最后,累加积水深度。若积水深度为负数,则等同于0。
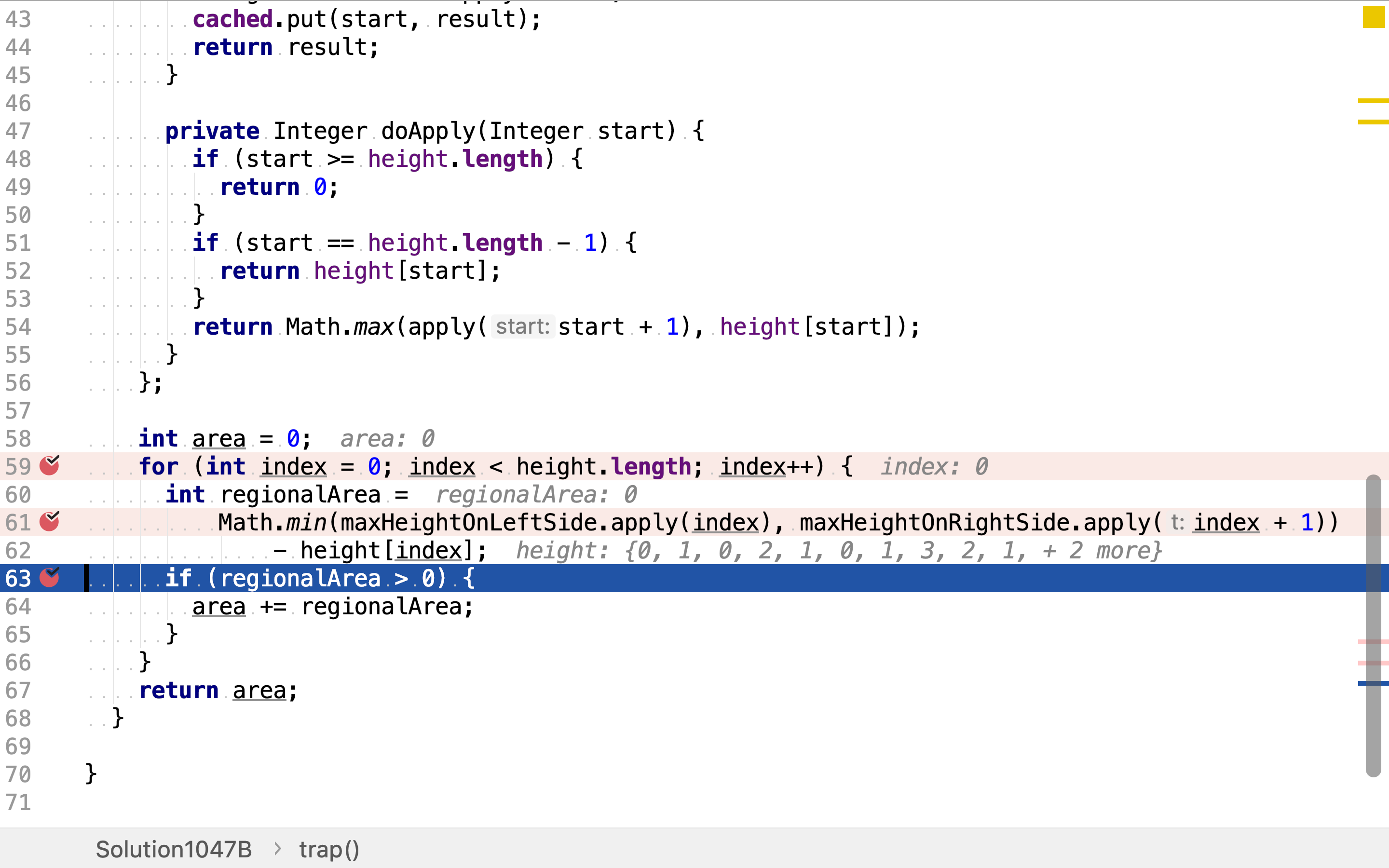
求左右边最高柱子的方法则使用带值缓存的函数实现。
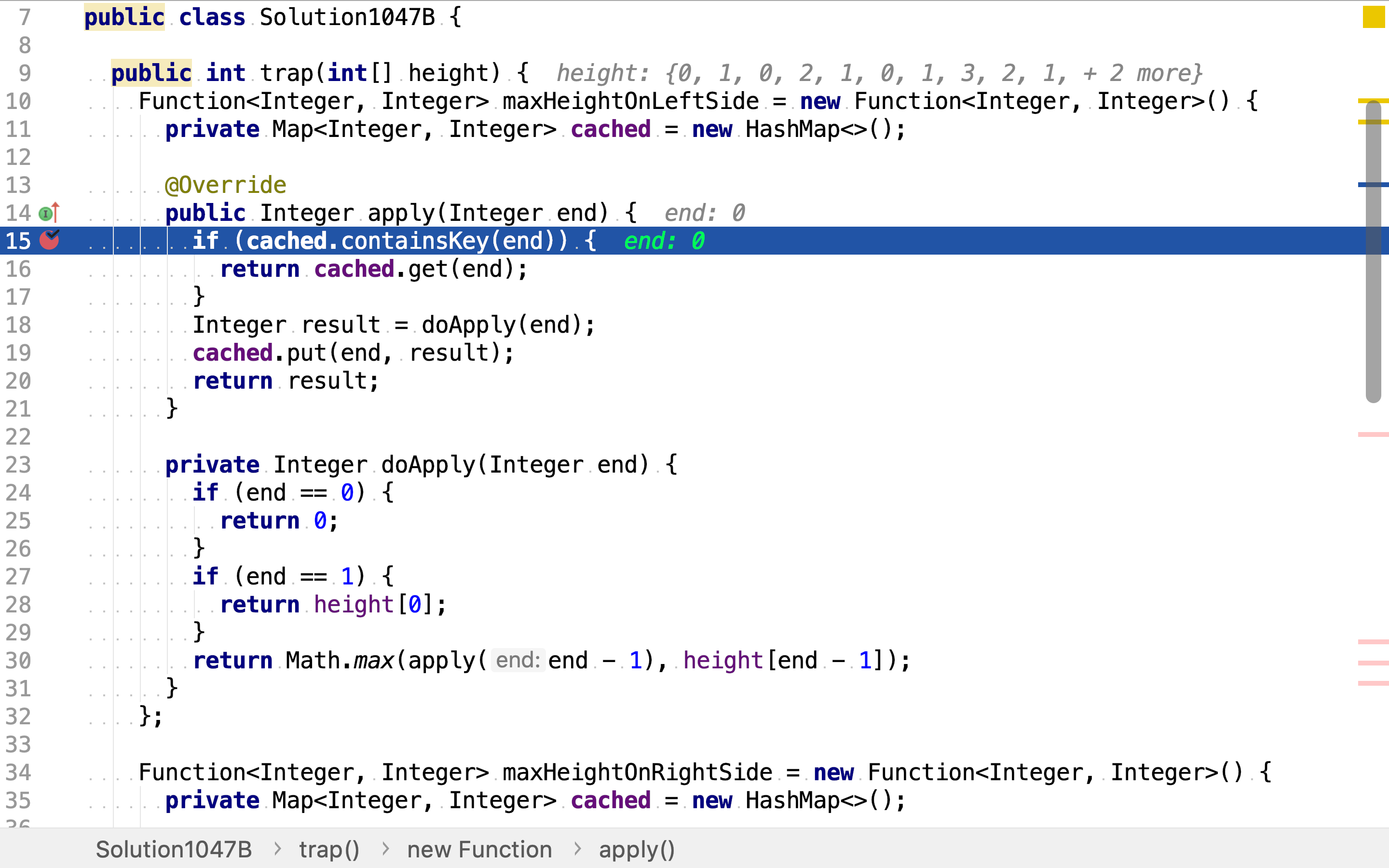
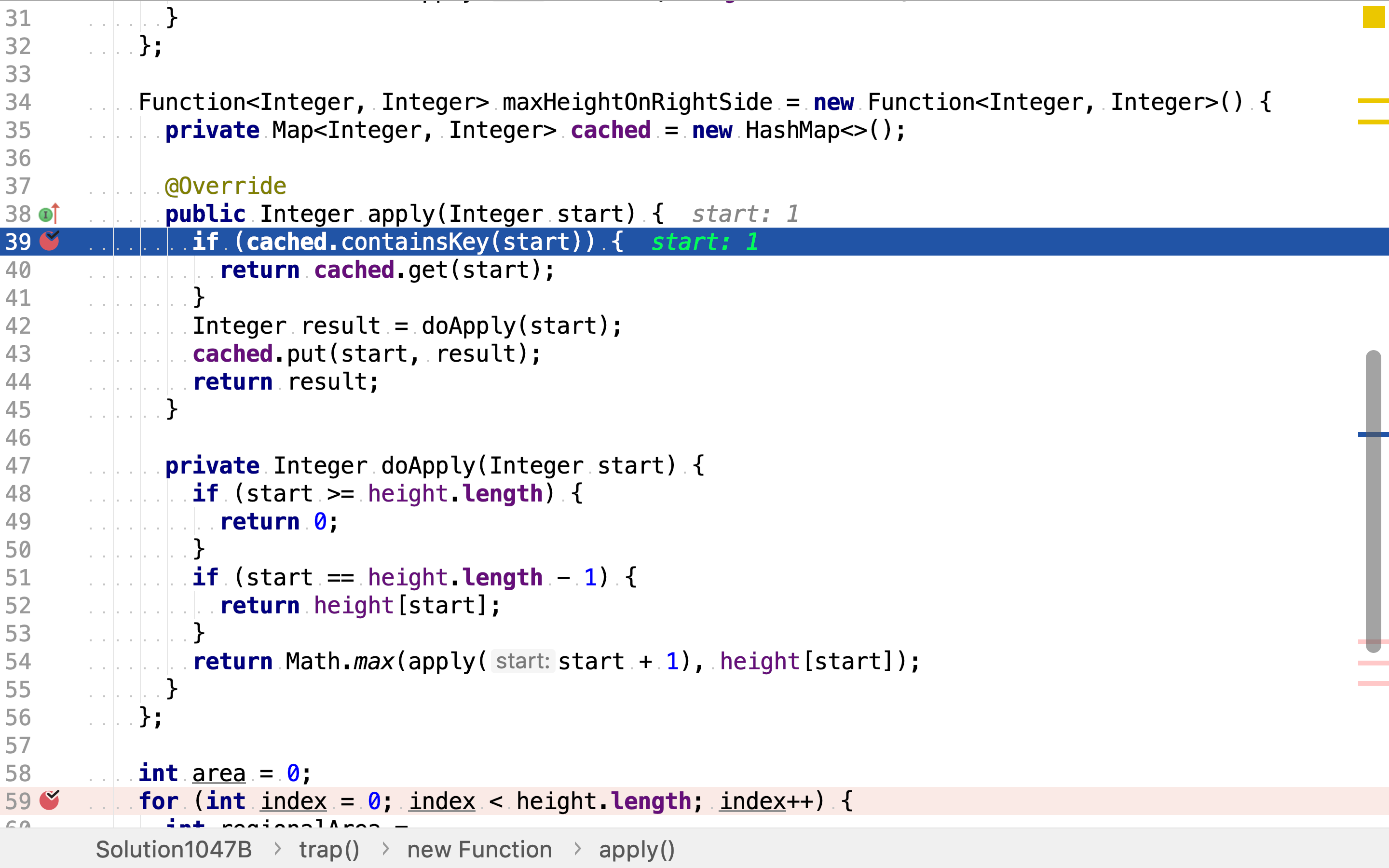
复杂度分析
时间复杂度
本演算法缓存了所有maxHeightOnLeftSide和maxHeightOnRightSide的值,所以实际上只遍历了一遍所有柱子。所以时间复杂度为。
空间复杂度
本演算法缓存了所有maxHeightOnLeftSide和maxHeightOnRightSide的值。所以空间复杂度是。
双指针法
要计算某一柱子上积水高度,并非一定要分别计算出左右边最高的柱子,而只需要计算出左右边最高柱子中的较低者。
使用左右两个指针,分别从左端和右端向中间移动。再将左指针左侧最大高度记为leftMaxHeight,右指针右侧最大高度记为rightMaxHeight。
当左指针指向柱子低于右指针柱子时,移动左指针;当左指针柱子高于右指针柱子时,移动右指针。
当移动左指针时,若所指柱子高于leftMaxHeight则更新之。且此时leftMaxHeight和rightMaxHeight中较低者即为左侧最高柱子和右侧最高柱子之中的较低者。
当移动右指针时,进行类似的操作。
举个例子,给定如下柱图:
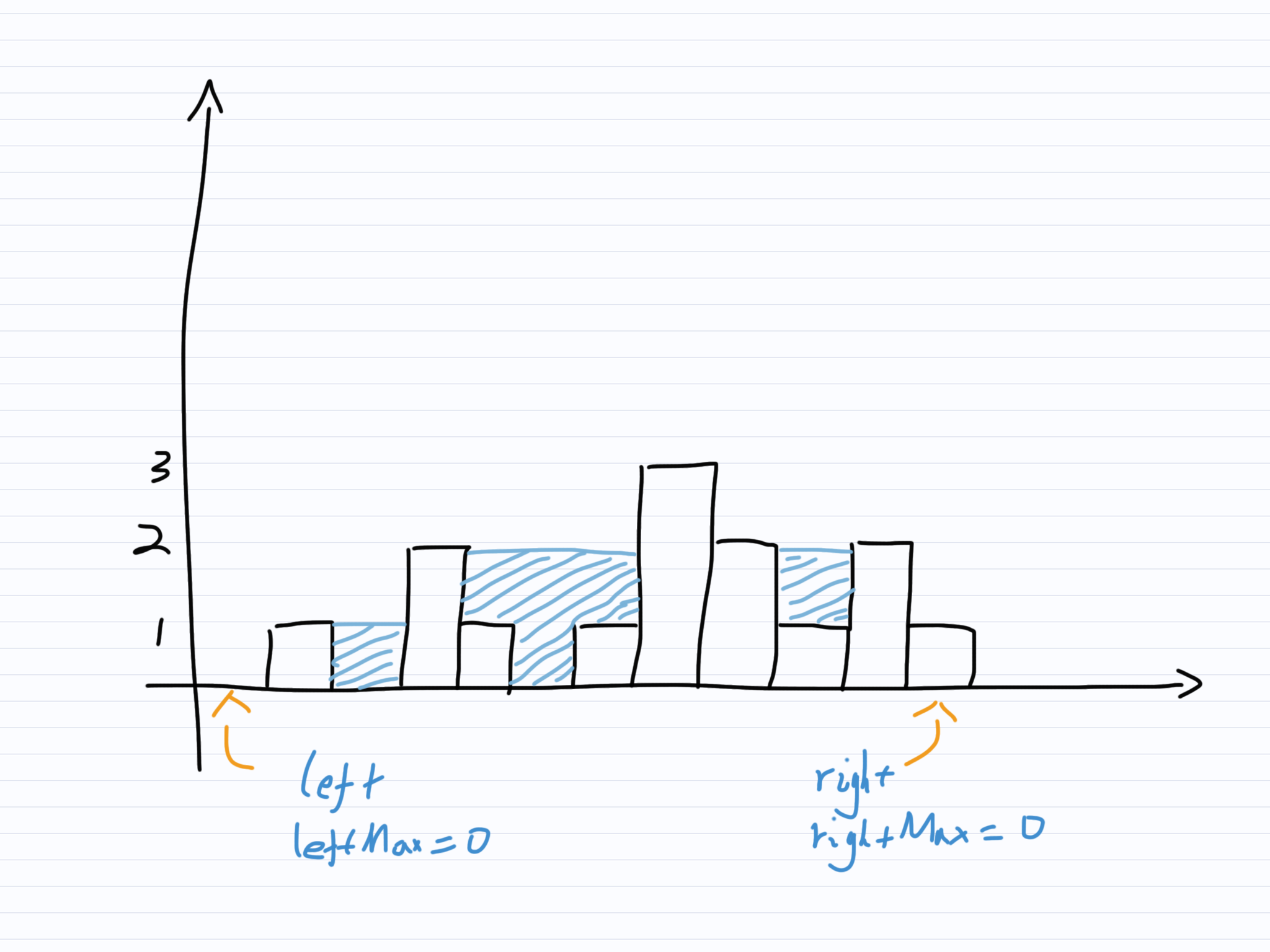
left, right指针初始分别指向头和尾端柱子,leftMax, rightMax初始为0。
比较左右指针所指柱子,左指针柱子低于右指针柱子,则移动左指针。移动指针前,若左指针所指柱子高于leftMax则更新leftMax,同累加左指针所指柱子上的积水深度。
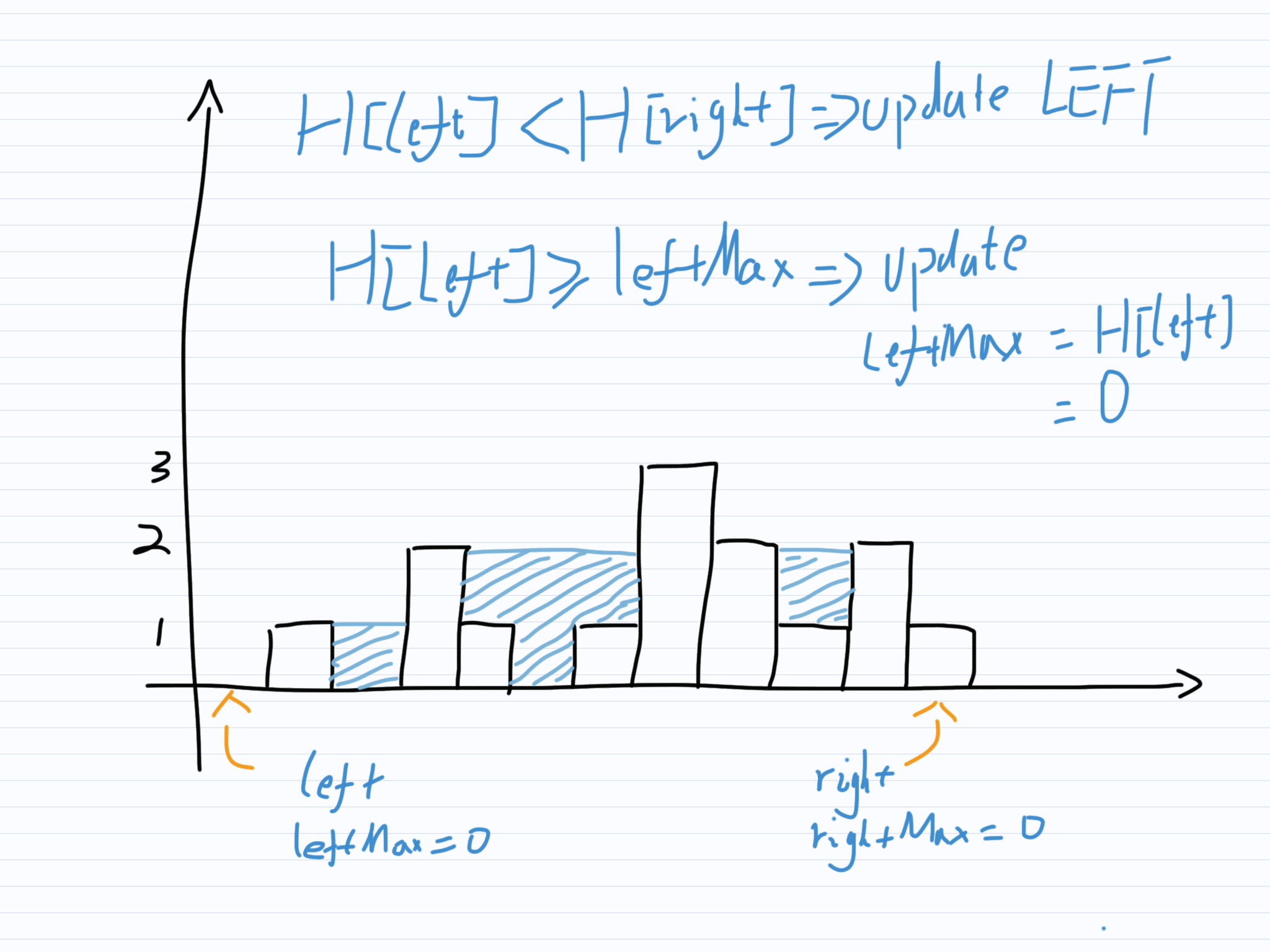
继续比较左右指针所指柱子,此时左指针所指柱子并没有低于右指针所指柱子,所以移动右指针。移动指针之前,若右指针所指柱子高于rightMax则更新rightMax。同时累计右指针所指柱子上的积水深度。
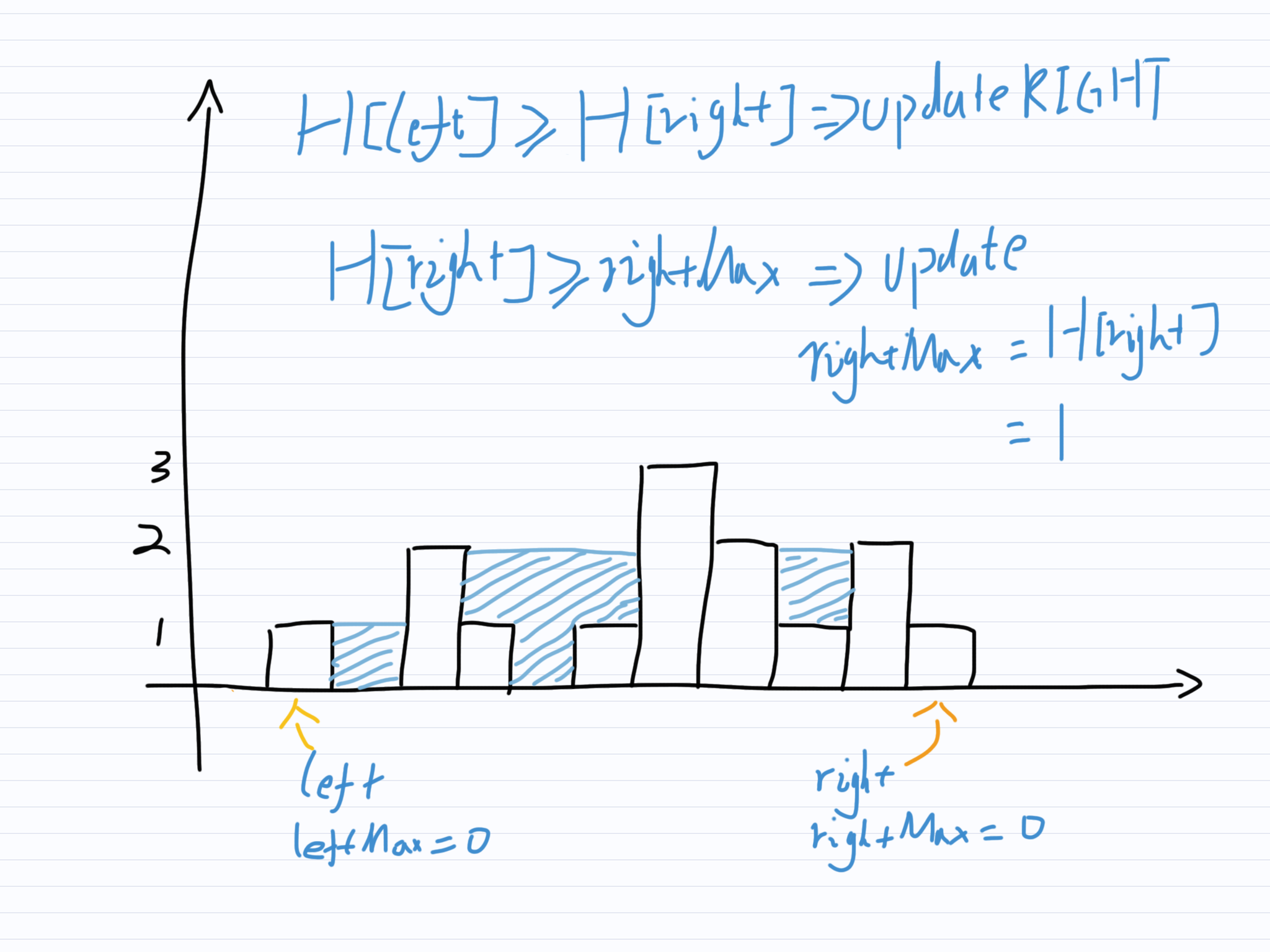
继续比较左右指针所指柱子,此时左指针所指柱子低于右指针所指柱子,移动左指针。移动左指针之前,若左指针所指柱子高于leftMax则更新leftMax。同时累计左指针所指柱子上的积水深度。

代码实现
首先,创建左右双指针分别指向头和尾。同时创建leftMaxHeight和rightMaxHeight。
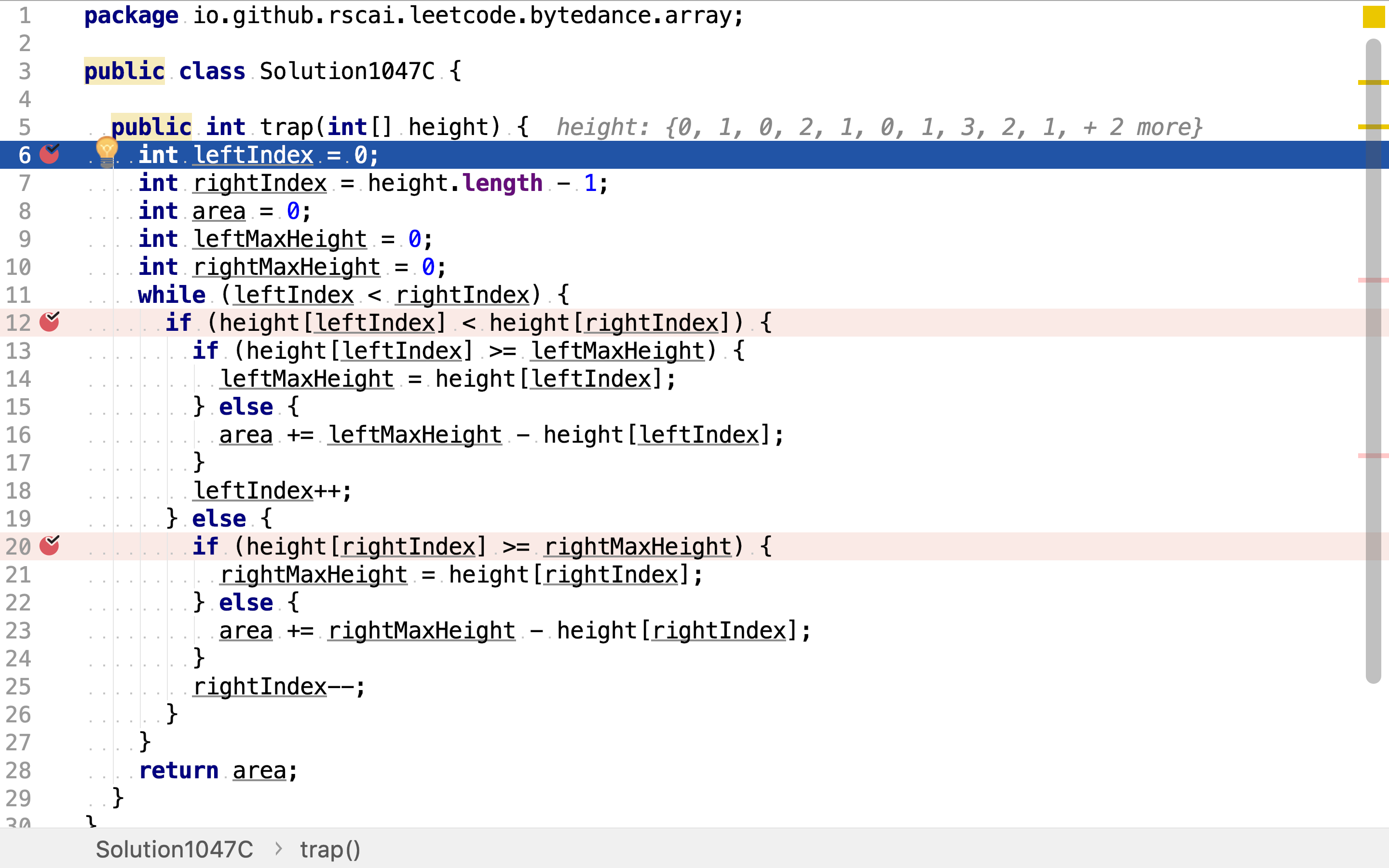
然后,向中间移动双指针。当左指针所指柱子低于右指针所指柱子时,移动左指针。若新的柱子高于leftMaxHeight则更新之;否则计算新柱子上积水深度并累计。
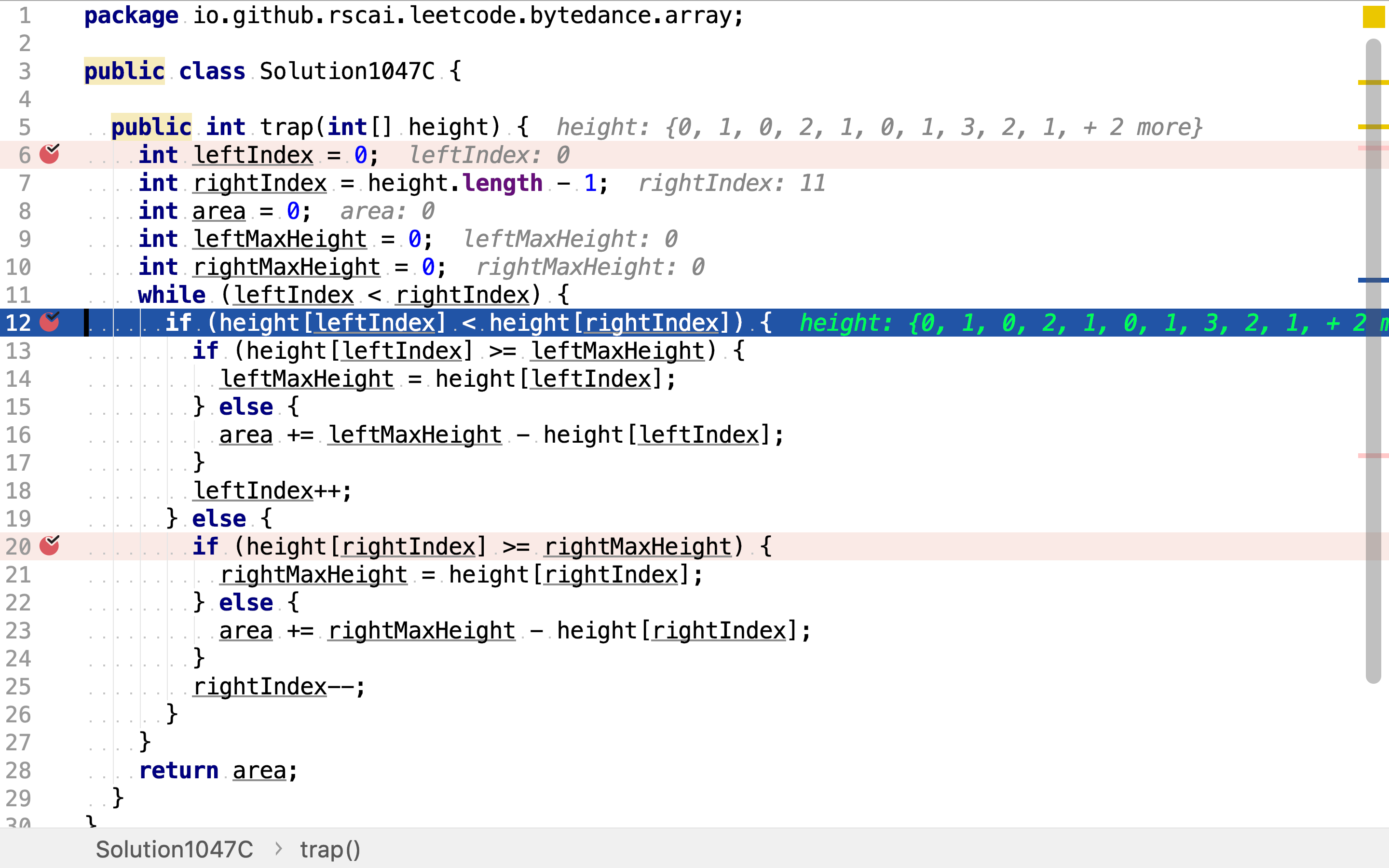
当左指针高于右指针时,移动右指针。若新的柱子高于rightMaxHeight则更新之;否则计算新柱子上积水深度并累计。
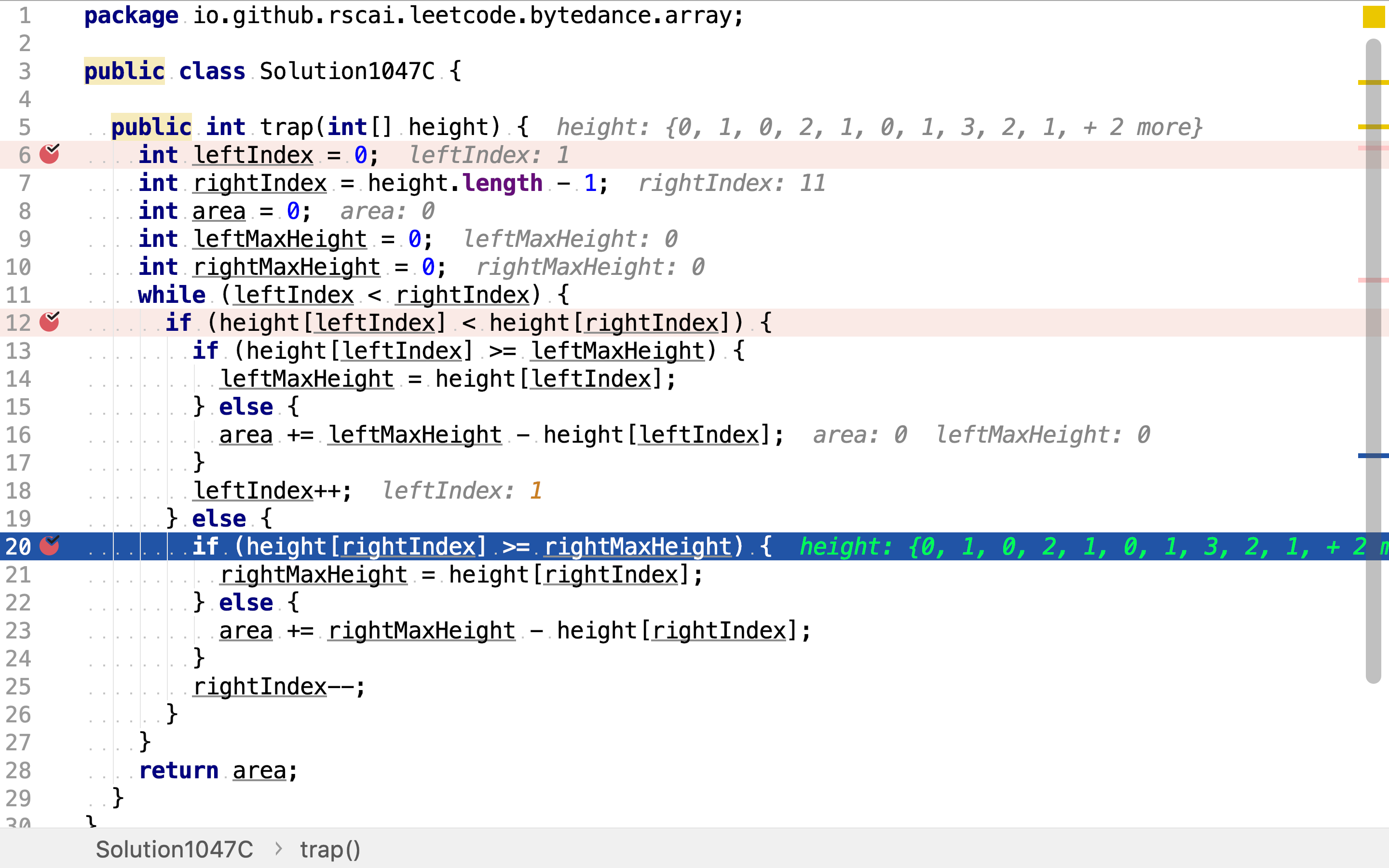
复杂度分析
时间复杂度
整共就遍历了一次所有柱子,所以时间复杂度是。
空间复杂度
使用了5个变量leftIndex, rightIndex, area, leftMaxHeight, rightMaxHeight,空间复杂度为。
