买卖股票的最佳时机 II

题目

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例1：

输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
    随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

示例2：

输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
    注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。
    因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例3：

输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

穷举法

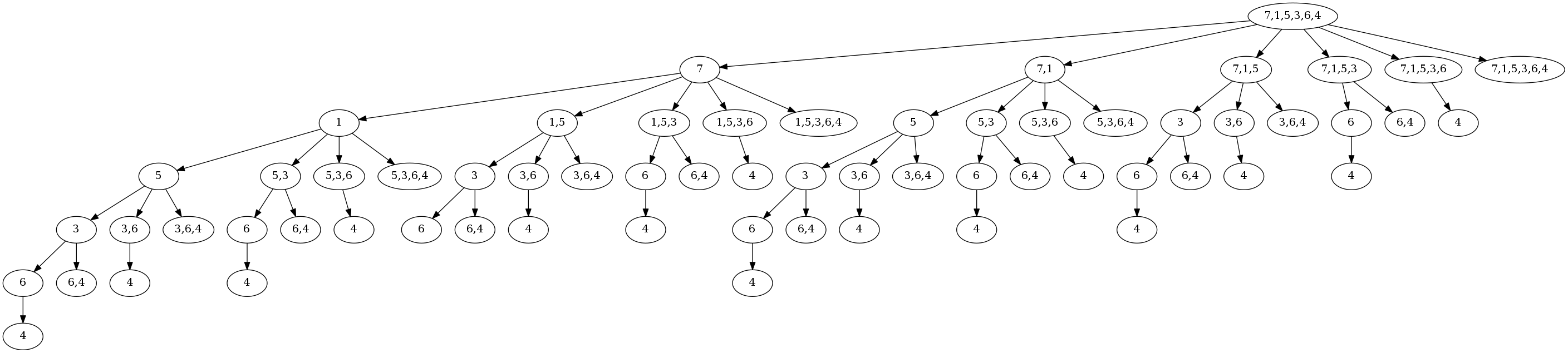
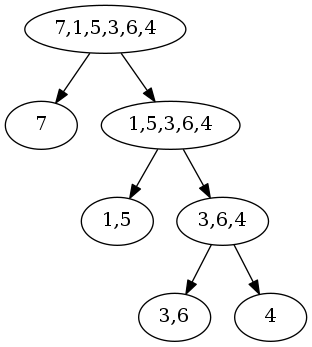
罗列所有的买卖组合，再计算其中利润最大的组合。多次买卖由第一次买卖和后续买卖组成，后续买卖只能在第一次卖出点之后发生。用树表示所有买卖组合，第一层为可选的第一次买卖组合（根节点为第零层，同一天买卖等同于当天不买卖），第N层为第N次买卖。

举个例子，给定价格序列[7, 1, 5, 3, 6, 4]。第一次买卖有六种选择：

  1. 以7的价格买入，以7的价格卖出。等同于第一天不买卖。
  2. 以7的价格买入，以1的价格卖出。
  3. 以7的价格买入，以5的价格卖出。
  4. 以7的价格买入，以3的价格卖出。
  5. 以7的价格买入，以6的价格卖出。
  6. 以7的价格买入，以4的价格卖出。

第二次买卖可行的选择由第一次买卖决定。第二次买卖的买入点一定是第一次买卖的卖出点后一天。依此类推。

代码

package io.github.rscai.leetcode.bytedance.dynamic; import java.util.stream.IntStream; import java.util.stream.Stream; public class Solution1043A { public int maxProfit(int[] prices) { Stream<IntStream> allProfitSeqs = profitSeqs(prices, 0); return allProfitSeqs.map(profitSeq -> profitSeq.sum()).mapToInt(Integer::valueOf).max() .orElse(0); } private Stream<IntStream> profitSeqs(int[] prices, int start) { if (start >= prices.length) { return Stream.of(IntStream.empty()); } Stream<IntStream> profitSeqs = Stream.empty(); int buyAt = start; for (int sellAt = buyAt; sellAt < prices.length; sellAt++) { int profit = prices[sellAt] - prices[buyAt]; Stream<IntStream> remainProfitSeqs = profitSeqs(prices, sellAt + 1); profitSeqs = Stream.concat(profitSeqs, remainProfitSeqs .map(remainProfitSeq -> IntStream.concat(IntStream.of(profit), remainProfitSeq))); } return profitSeqs; } }

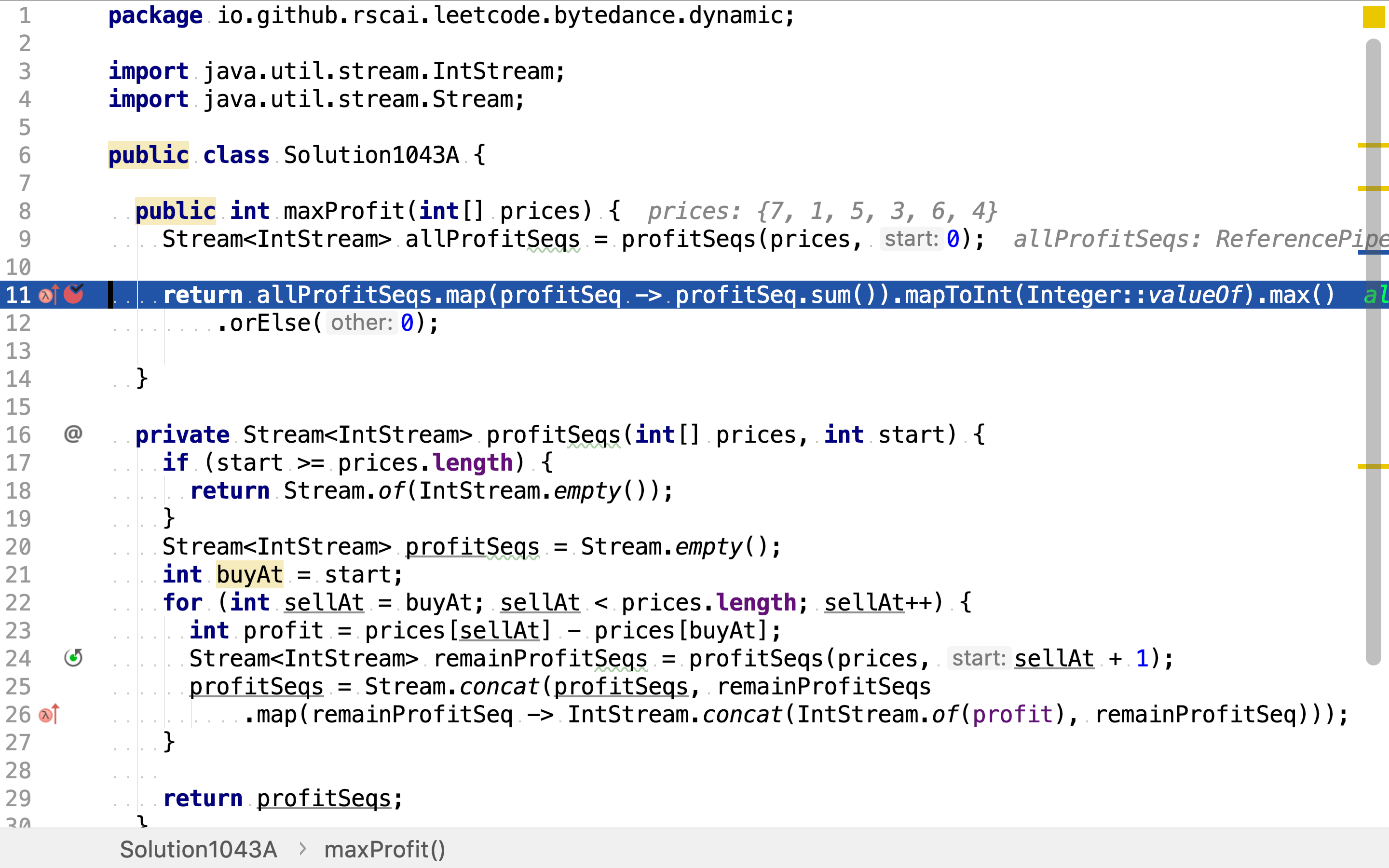
首先，在第一天买进，罗列出所有的卖出选择　包括当天卖出。

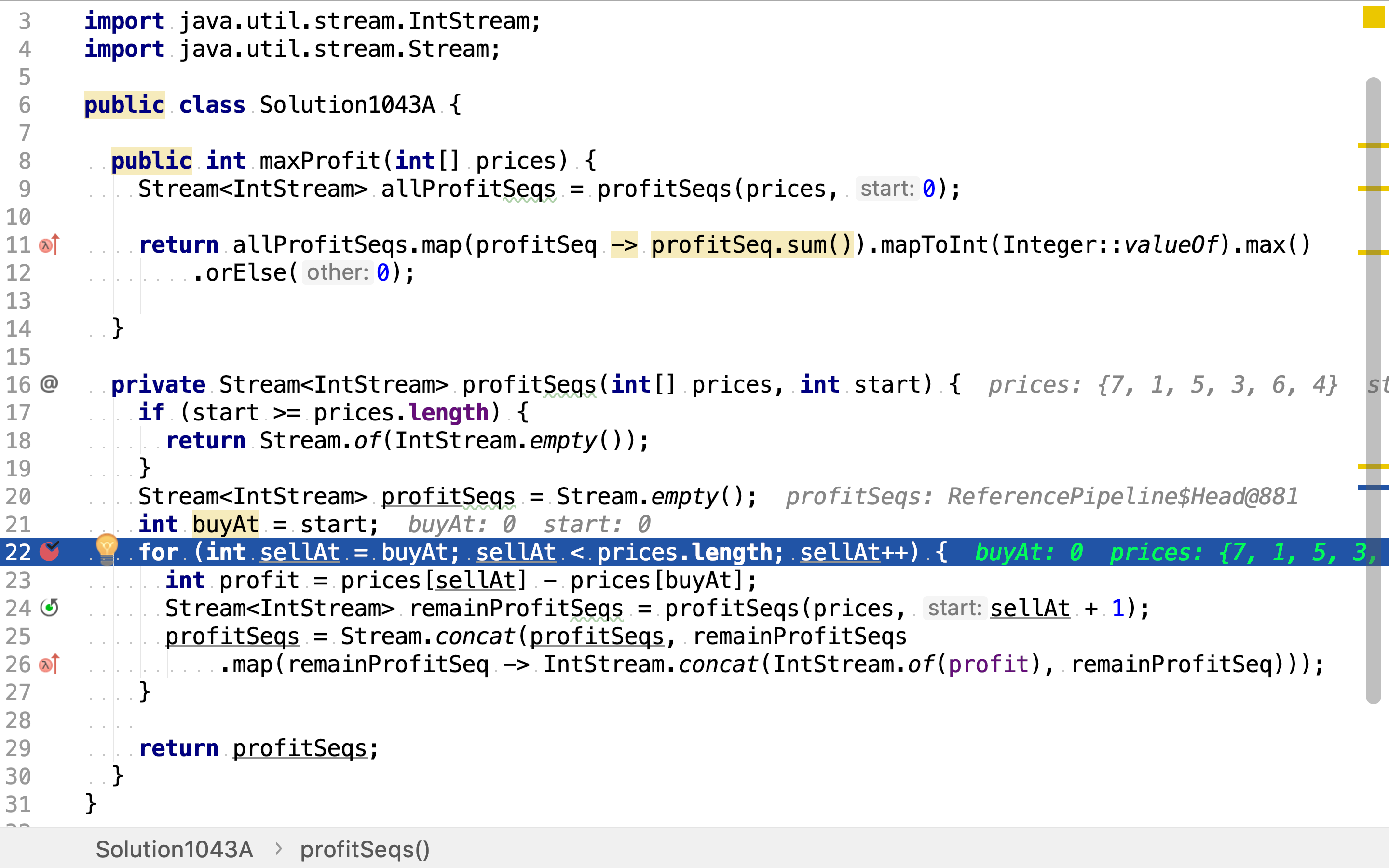
debug-A1

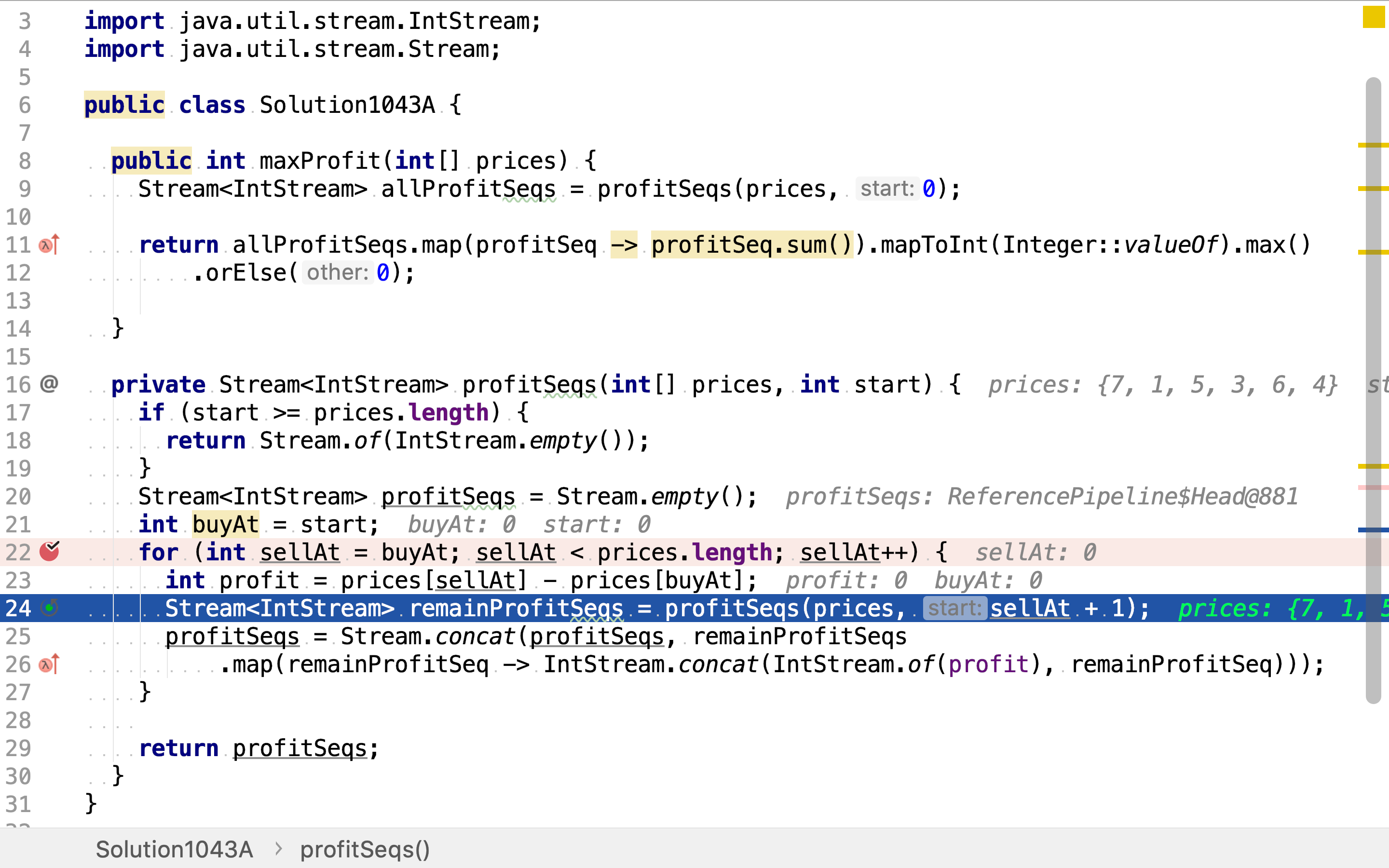
然后，罗列出在剩余价格序列中的买卖序列组合。剩余价格序列由这一次卖出点决定。所以不同的当次买卖产生不同的剩余价格序列，也产了不同的剩余买卖序列组合。

debug-A2

再然后，组合当次买卖与剩余买卖序列组合，构成新的买卖序列组合。

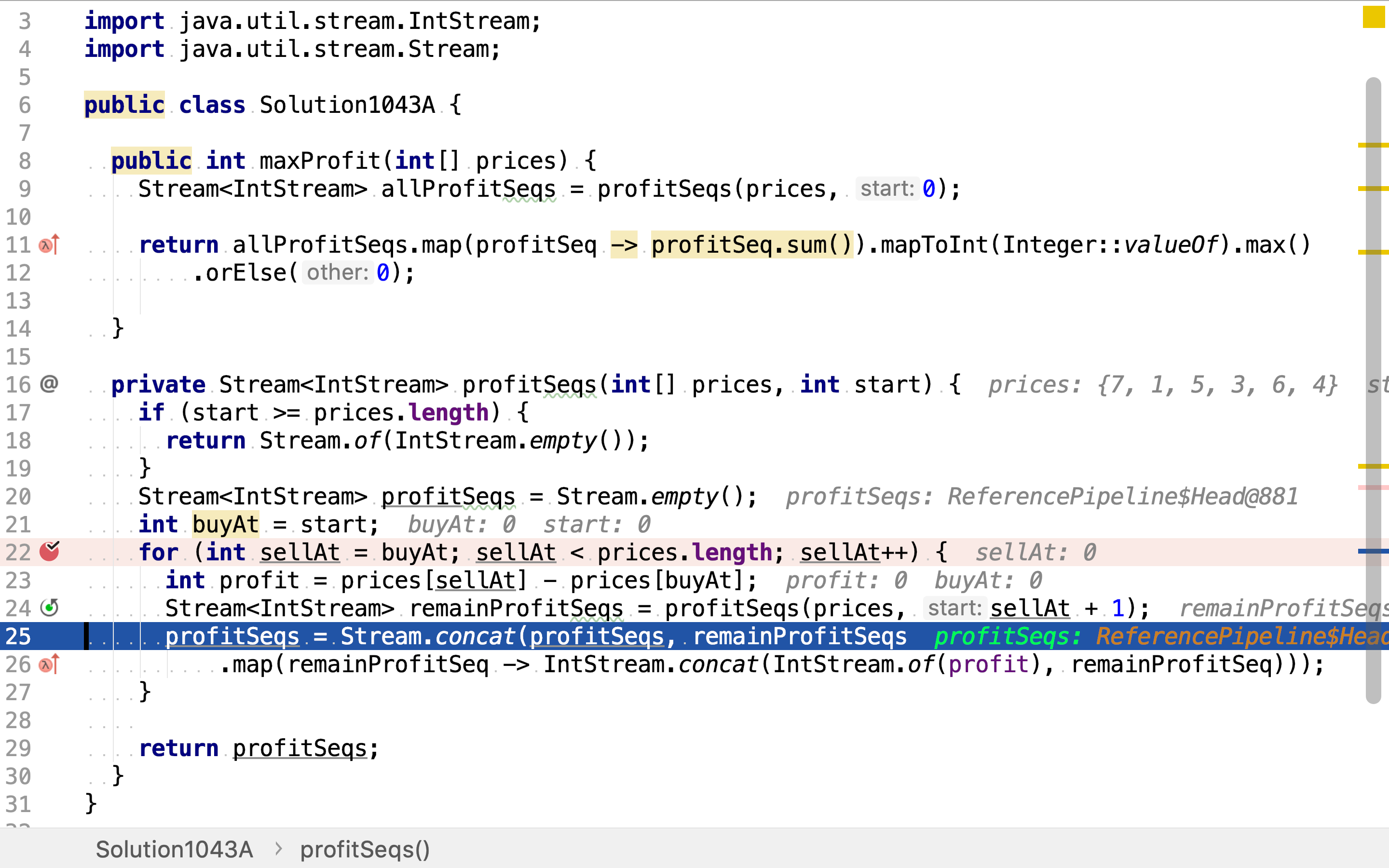
debug-A3

最后，合计所有的买卖序列产生的利润，从中取最大值。

debug-A4

复杂度分析

时间复杂度

时间复杂度为：

空间复杂度

空间复杂度等于树的最大深度，为

贪婪算法

在第一天买入，如果利润持续增加（第二天的价格大于今天）则持有。若利润下降（第二天价格低于当天）则卖出。（可同一天买卖，等同于当天不交易）。然后，在剩余价格序列中重复相同的操作。

举个例子，给定价格序列[7, 1, 5, 3, 6, 4]。

  • 第一次，在7买入，在7卖出。等同于不交易。剩余价格序列[1, 5, 3, 6, 4]
  • 第二次，在1买入，在5卖出。剩余价格序列[3, 6, 4]
  • 第三次，在3买入，在6卖出。剩余价格序列[4]
  • 第四次，在4买入，在4卖出。等同于交易。

代码

package io.github.rscai.leetcode.bytedance.dynamic; public class Solution1043B { public int maxProfit(int[] prices) { int maxProfit = 0; int remainStart = 0; while (remainStart < prices.length) { int[] profitAndRemainStart = profit(prices, remainStart); maxProfit = maxProfit + profitAndRemainStart[0]; remainStart = profitAndRemainStart[1]; } return maxProfit; } private int[] profit(int[] prices, int start) { int profit = 0; for (int sellAt = start + 1; sellAt < prices.length; sellAt++) { if (prices[sellAt] - prices[sellAt - 1] < 0) { return new int[]{profit, sellAt}; } else { profit = profit + prices[sellAt] - prices[sellAt - 1]; } } return new int[]{profit, prices.length}; } }

首先，在第一天买入，在利润开始下降前卖出（同天买卖等同于不交易）。得到利润和剩余价格序列（这𥚃用剩余价格序列开始下标）。

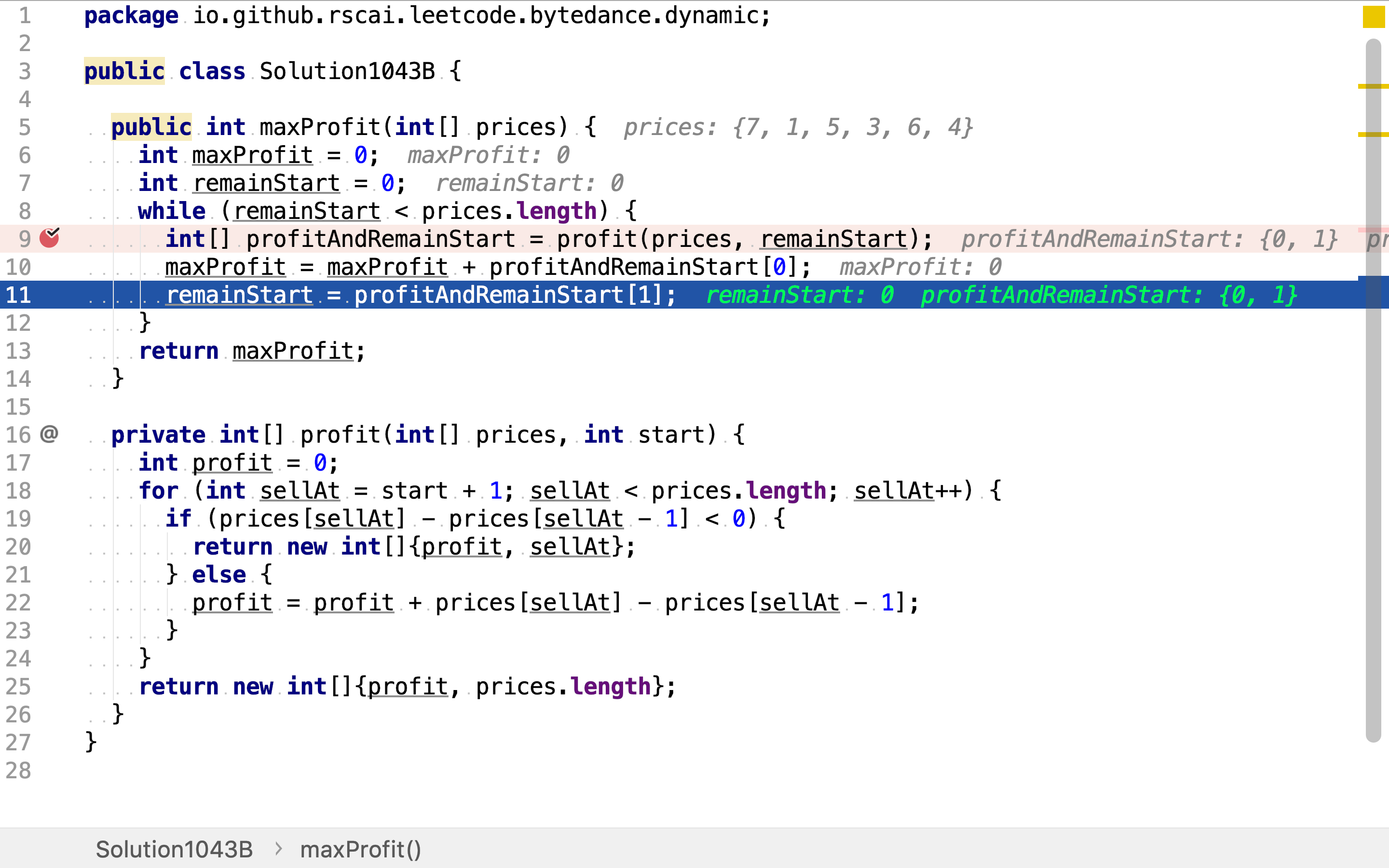
debug-B1

然后，如果剩余价格列表不空，则继续在第一天（剩余序列中的第一天）买入，在利润开始下降前卖出。得到利润和剩余价格序列。

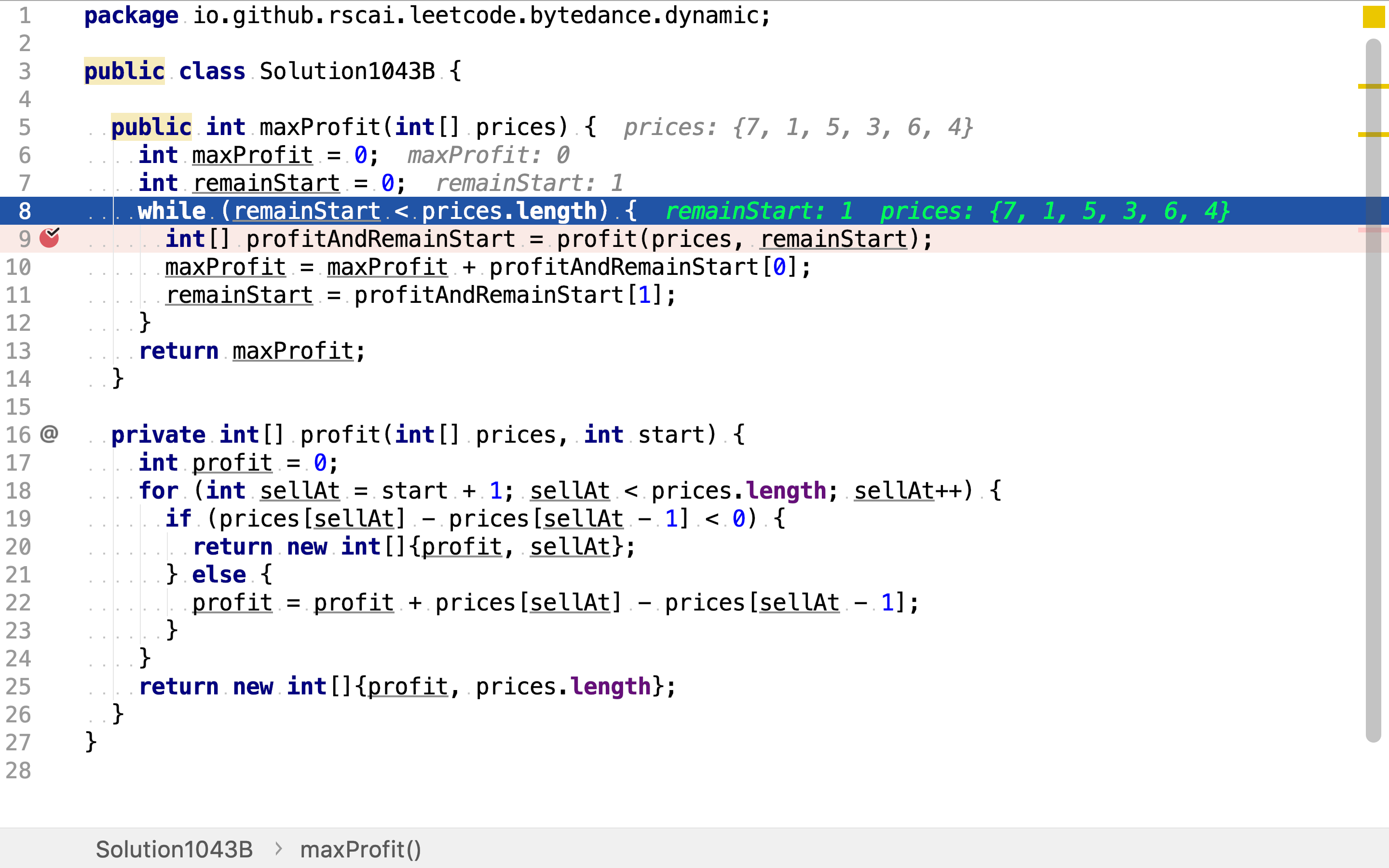
debug-B2

在第一天买入，如果价格在上升意味着利润增加，应继续持有。如果价格下降则意味着利润下降，应在价格下降前卖出。

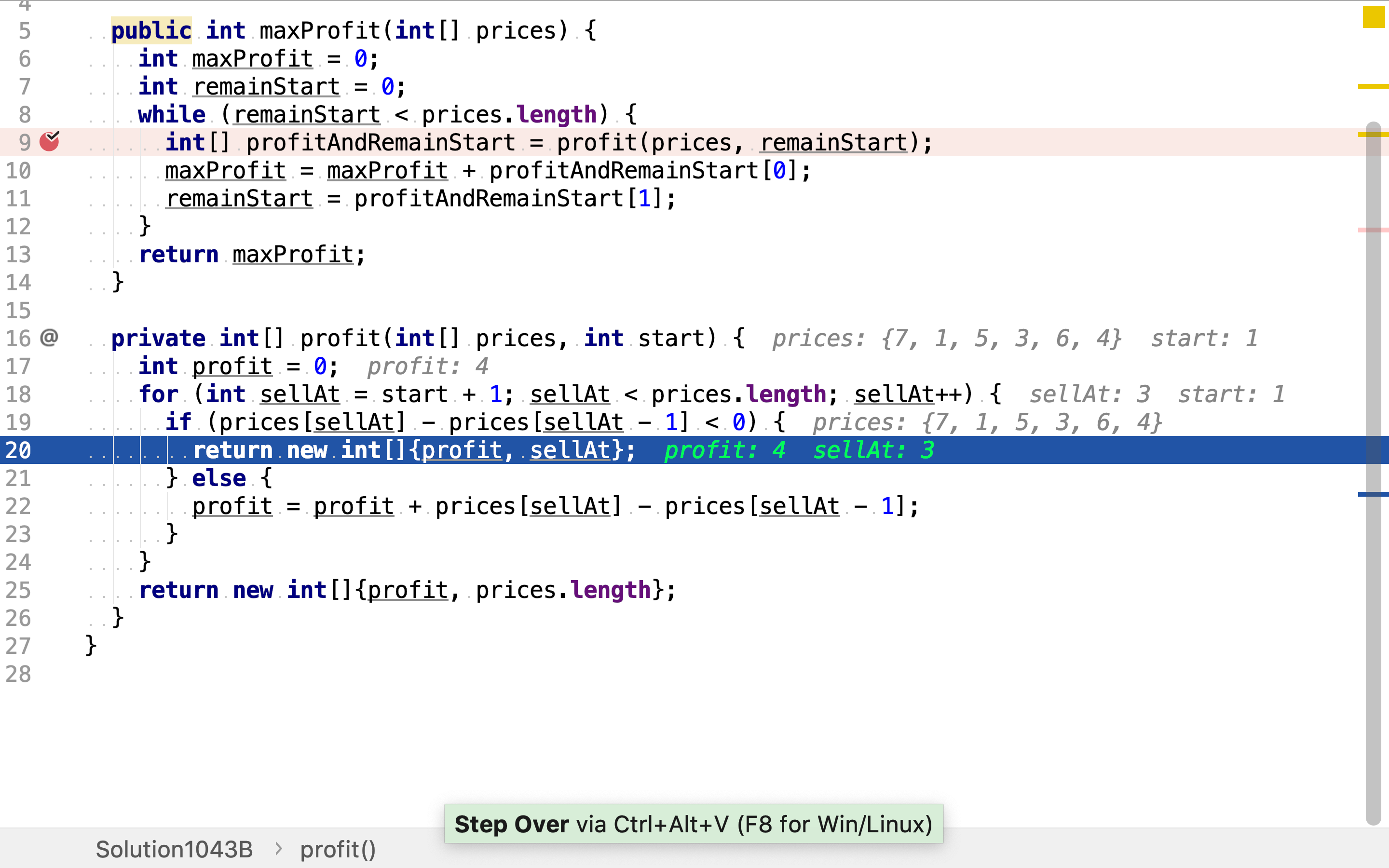
debug-B3

复杂度分析

时间复杂度

时间复杂度等于profit被调用的次数及每次profit中遍历价格序列的长度，其等于整个价格序列的长度。所以，时间复杂度为：

空间复杂度

只有三毎变量maxProfit, remainStart和profit。

results matching ""

    No results matching ""