翻转字符串里的单词

题目

给定一个字符串，逐个翻转字符串中的每个单词。

示例 1：

输入: "the sky is blue"
输出: "blue is sky the"

示例 2:

输入: " hello world! "
输出: "world! hello"
解释: 输入字符串可以在前面或者后面包含多余的空格，但是反转后的字符不能包括。

示例 3：

输入: "a good example"
输出: "example good a"
解释: 如果两个单词间有多余的空格，将反转后单词间的空格减少到只含一个。

说明：

• 无空格字符构成一个单词。
• 输入字符串可以在前面或者后面包含多余的空格，但是反转后的字符不能包括。
• 如果两个单词间有多余的空格，将反转后单词间的空格减少到只含一个。

进阶：

请选用 C 语言的用户尝试使用 O(1) 额外空间复杂度的原地解法。

解柝单词法

先将字符串中的单词一一解出，再将单词反序，最后将反序的单词拼接成字符串。

代码实现

先将字符串拆分为单词序列，

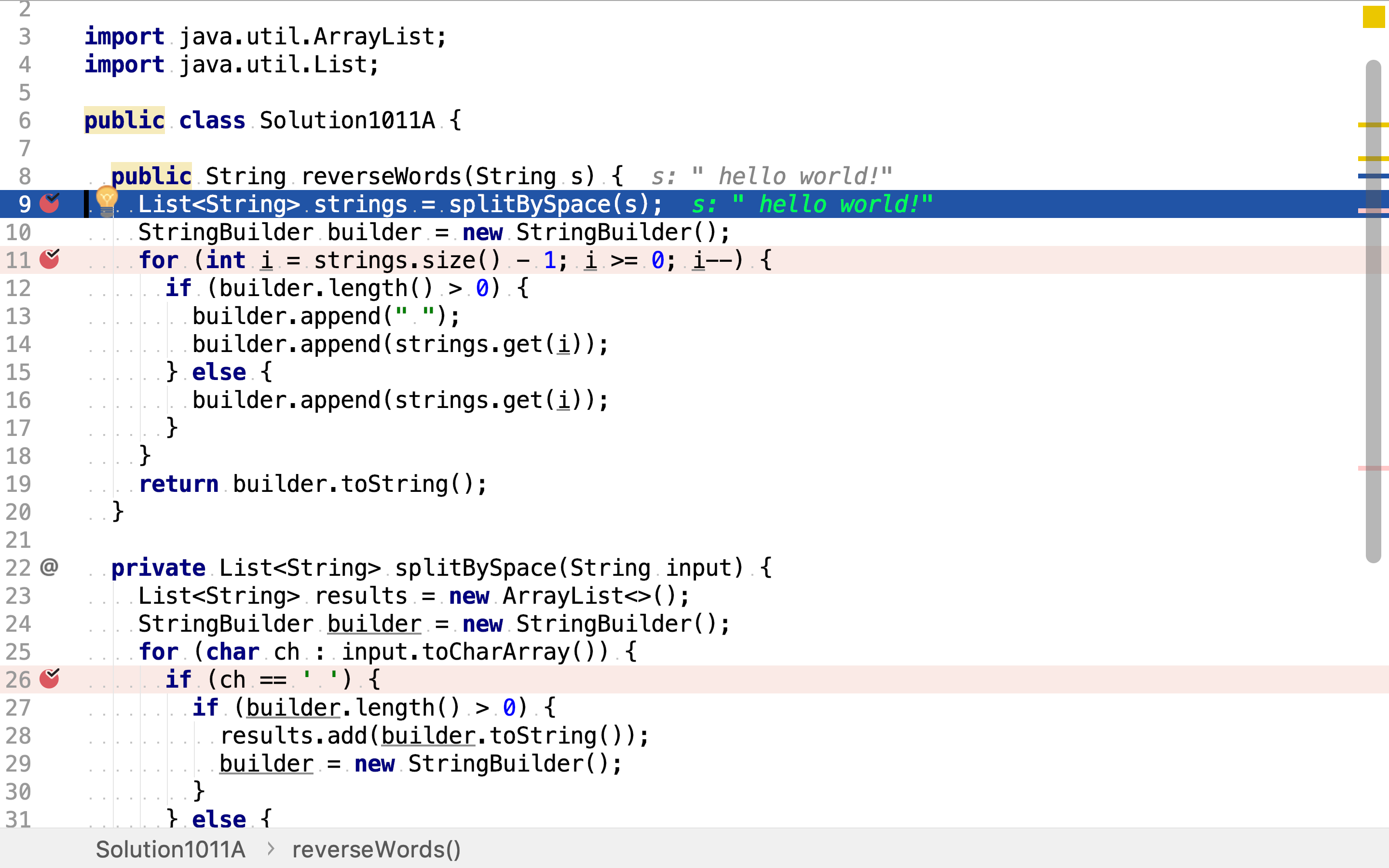
再将单词序列反序，并拼接成新的字符串。

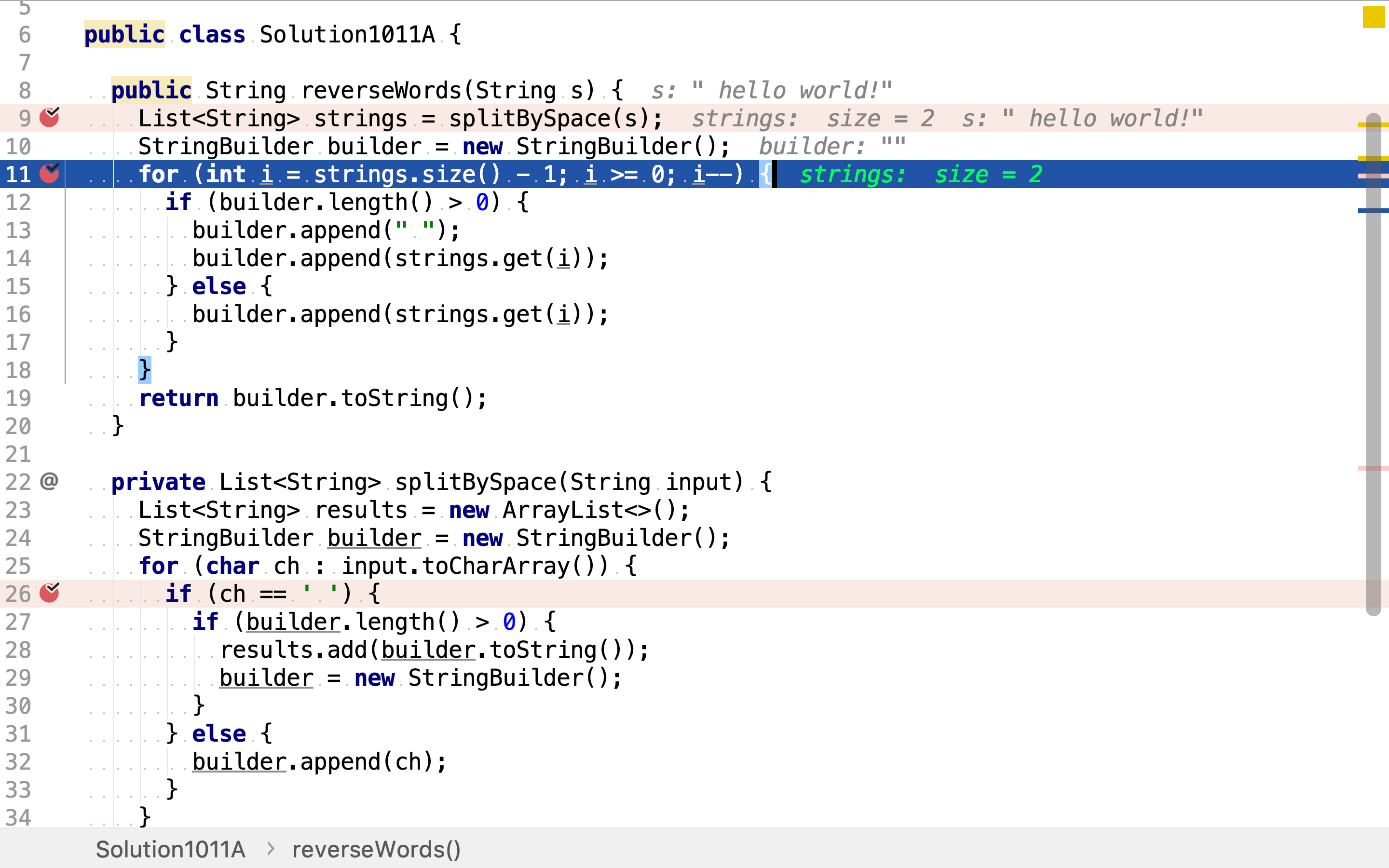
「单词拆分」使用「确定有限状态机」实现。

确定有限状态自动机

在计算理论中，确定有限状态自动机或确定有限自动机（英语：deterministic finite automaton, DFA）是一个能实现状态转移的自动机。对于一个给定的属于该自动机的状态和一个属于该自动机字母表 $\Sigma$ 的字元，它都能根据事先给定的转移函式转移到下一个状态（这个状态可以是先前那个状态）。

基础概念

定义

确定有限状态自动机 ${\mathcal {A}}$ 是由

• 一个非空有限的状态集合 $Q$
• 一个输入字母表 $\Sigma$ （非空有限的字元集合）
• 一个转移函式 $\delta :Q\times \Sigma \rightarrow Q$（例如： $\delta \left(q,\sigma \right)=p,\left(p,q\in Q,\sigma \in \Sigma \right)$）
• 一个开始状态 $s\in Q$
• 一个接受状态的集合 $F\subseteq Q$

所组成的5-元组。因此一个DFA可以写成这样的形式： ${\mathcal {A}}=\left(Q,\Sigma ,\delta ,s,F\right)$。

工作方式（非正式的语意)

确定有限状态自动机从起始状态开始，一个字元接一个字元地读入一个字串 $w\in \Sigma ^{*}$（这里的 ${}^{*}$指示Kleene星号算子。），并根据给定的转移函式一步一步地转移至下一个状态。在读完该字串后，如果该自动机停在一个属于F的接受状态，那么它就接受该字串，反之则拒绝该字串。

扩充转移函式

为了在保证严谨的前提下，方便地叙述关于DFA的内容，我们定义如下扩充的转移函式：$\delta ^{*}:Q\times \Sigma ^{*}\rightarrow Q$。

• 其中$\delta ^{*}\left(q,w\right)$是自动机从状态q顺序读入字串w后达到的状态
• 扩充转移函式递回的定义为：
  • $\delta ^{*}\left(q,\epsilon \right)=q$
  • $\delta ^{*}\left(q,u\sigma \right)=\delta (\delta ^{*}(q,u),\sigma ),\forall u\in \Sigma ^{*},\sigma \in \Sigma$

工作方式（正式的语意）

对于一个确定有限状态自动机 ${\mathcal {A}}=\left(Q,\Sigma ,\delta ,s,F\right)$，如果 $\delta ^{*}\left(s,w\right)\in F$，我们就说该自动机接受字串w，反之则表明该自动机拒绝字串w。

被一个确定有限自动机接受的语言（或者叫「被辨识的语言」）定义为： ${\mathcal {L}}({\mathcal {A}})=\{w\in \Sigma ^{*}|{\mathcal {A}}~接受字串 ~w\}，$也就是由所有被接受的字串组成的集合。

参考

• 确定有限状态自动机

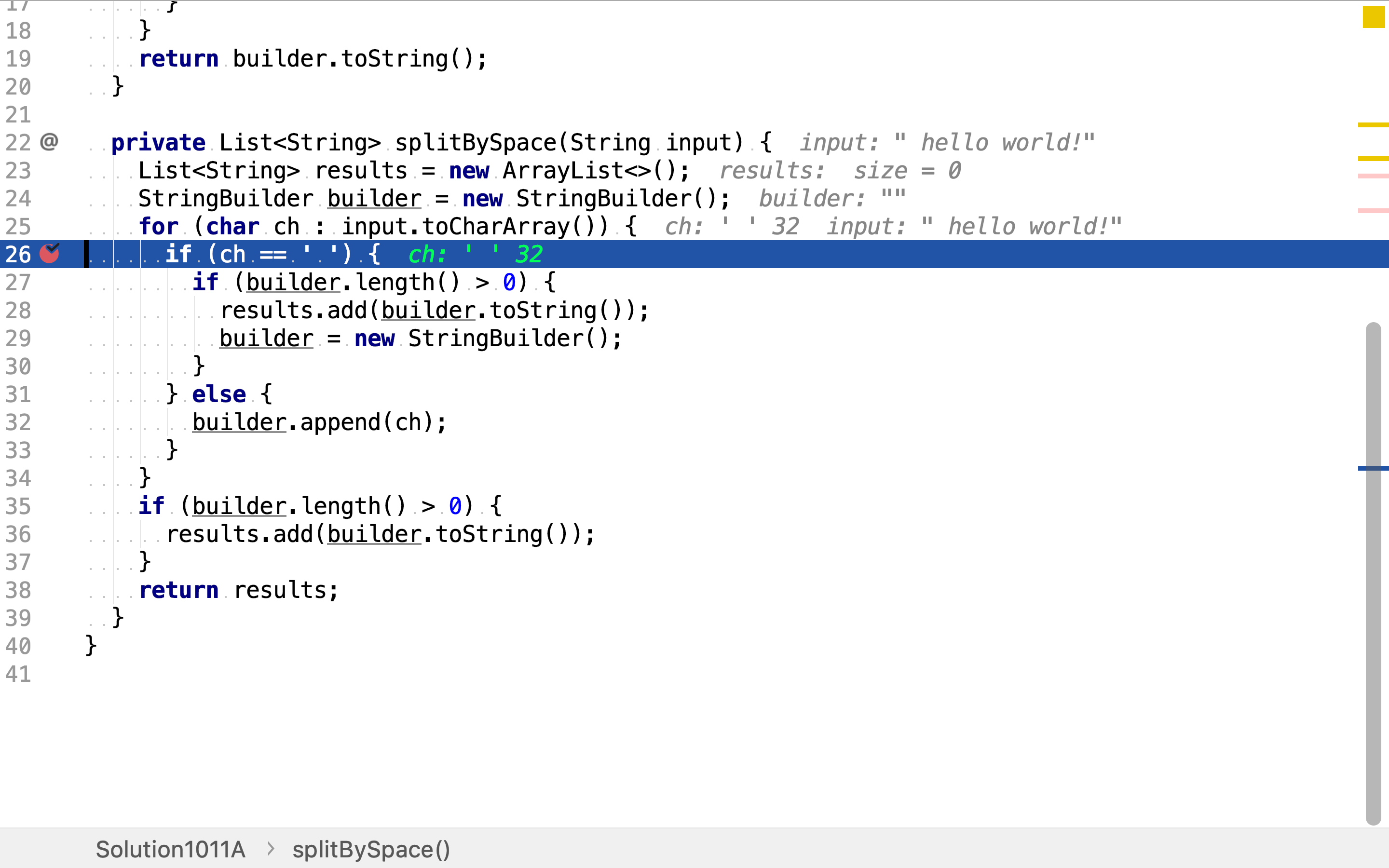
本例中，当遇到字符「空格」时，将暂存在builder中的字符较出为单词；当遇到非空格字符时，将其暂存至builder中。

复杂度分析

时间复杂度

拆解单词需遍历一遍输入字符串，反序构建字符串时遍历了一遍所有单词。所以时间复杂度为$\mathcal{O}(n)$。

空间复杂度

使用了变量strings, builder，其分别最多佔用n个空间。所以空间复杂度为$\mathcal{O}(n)$。