环形链表 II
题目
给定一个链表,返回链表开始入环的第一个节点。如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。
说明:不允许修改给定的链表。
示例1:
输入:head = [3,2,0,-4], pos = 1
输出:tail connects to node index 1
解释:链表中有一个环,其尾部连接到第二个节点。

示例2:
输入:head = [1,2], pos = 0
输出:tail connects to node index 0
解释:链表中有一个环,其尾部连接到第一个节点。

示例3:
输入:head = [1], pos = -1
输出:no cycle
解释:链表中没有环。

进阶:
你是否可以不用额外空间解决此题?
记录访问历史法
将访问过的节点放入一个集合中。每次访问节点时,都检查是否已被访问过(已在集合中)。若是,则其为环的入口点。
举个例子,给定如下链表:
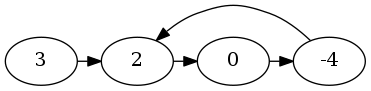
从头开始遍历,并将访问过的节点加入集合。

当䛀访问-4的后继时,发现其后继2已被访问过。所以2`就是入环点。
代码
package io.github.rscai.leetcode.bytedance.linktree;
/**
* Merge sort
*/
public class Solution1040A {
public ListNode sortList(ListNode head) {
int length = 0;
ListNode current = head;
while (current != null) {
length++;
current = current.next;
}
return mergeSort(head, length);
}
private ListNode mergeSort(ListNode head, int length) {
if (length == 0) {
return head;
}
if (length == 1) {
return head;
}
Object[] headLengths = binarySplit(head, length);
ListNode firstHead = (ListNode) headLengths[0];
int firstLength = (Integer) headLengths[1];
ListNode secondHead = (ListNode) headLengths[2];
int secondLength = (Integer) headLengths[3];
ListNode sortedFirst = mergeSort(firstHead, firstLength);
ListNode sortedSecond = mergeSort(secondHead, secondLength);
return merge(sortedFirst, sortedSecond);
}
private Object[] binarySplit(ListNode head, int length) {
int firstLength = Math.round(length / 2.0F);
int secondLength = length - firstLength;
ListNode secondHead = head;
ListNode firstTail = head;
for (int i = 0; i < firstLength; i++) {
firstTail = secondHead;
secondHead = secondHead.next;
}
firstTail.next = null;
return new Object[]{head, firstLength, secondHead, secondLength};
}
private ListNode merge(ListNode firstHead, ListNode secondHead) {
ListNode mergedHead = null;
ListNode mergedTail = null;
ListNode firstCurrent = firstHead;
ListNode secondCurrent = secondHead;
while (firstCurrent != null || secondCurrent != null) {
if (firstCurrent == null) {
ListNode secondNext = secondCurrent.next;
secondCurrent.next = null;
ListNode[] headAndTail = append(mergedHead, mergedTail, secondCurrent);
mergedHead = headAndTail[0];
mergedTail = headAndTail[1];
secondCurrent = secondNext;
} else if (secondCurrent == null) {
ListNode firstNext = firstCurrent.next;
firstCurrent.next = null;
ListNode[] headAndTail = append(mergedHead, mergedTail, firstCurrent);
mergedHead = headAndTail[0];
mergedTail = headAndTail[1];
firstCurrent = firstNext;
} else if (firstCurrent.val < secondCurrent.val) {
ListNode firstNext = firstCurrent.next;
firstCurrent.next = null;
ListNode[] headAndTail = append(mergedHead, mergedTail, firstCurrent);
mergedHead = headAndTail[0];
mergedTail = headAndTail[1];
firstCurrent = firstNext;
} else {
ListNode secondNext = secondCurrent.next;
secondCurrent.next = null;
ListNode[] headAndTail = append(mergedHead, mergedTail, secondCurrent);
mergedHead = headAndTail[0];
mergedTail = headAndTail[1];
secondCurrent = secondNext;
}
}
return mergedHead;
}
private ListNode[] append(ListNode head, ListNode tail, ListNode node) {
if (tail == null) {
head = node;
tail = head;
} else {
tail.next = node;
tail = node;
}
return new ListNode[]{head, tail};
}
}
从头开始遍历,针对每一个元素都先检查是否已被访问过。若是,则是入环点。
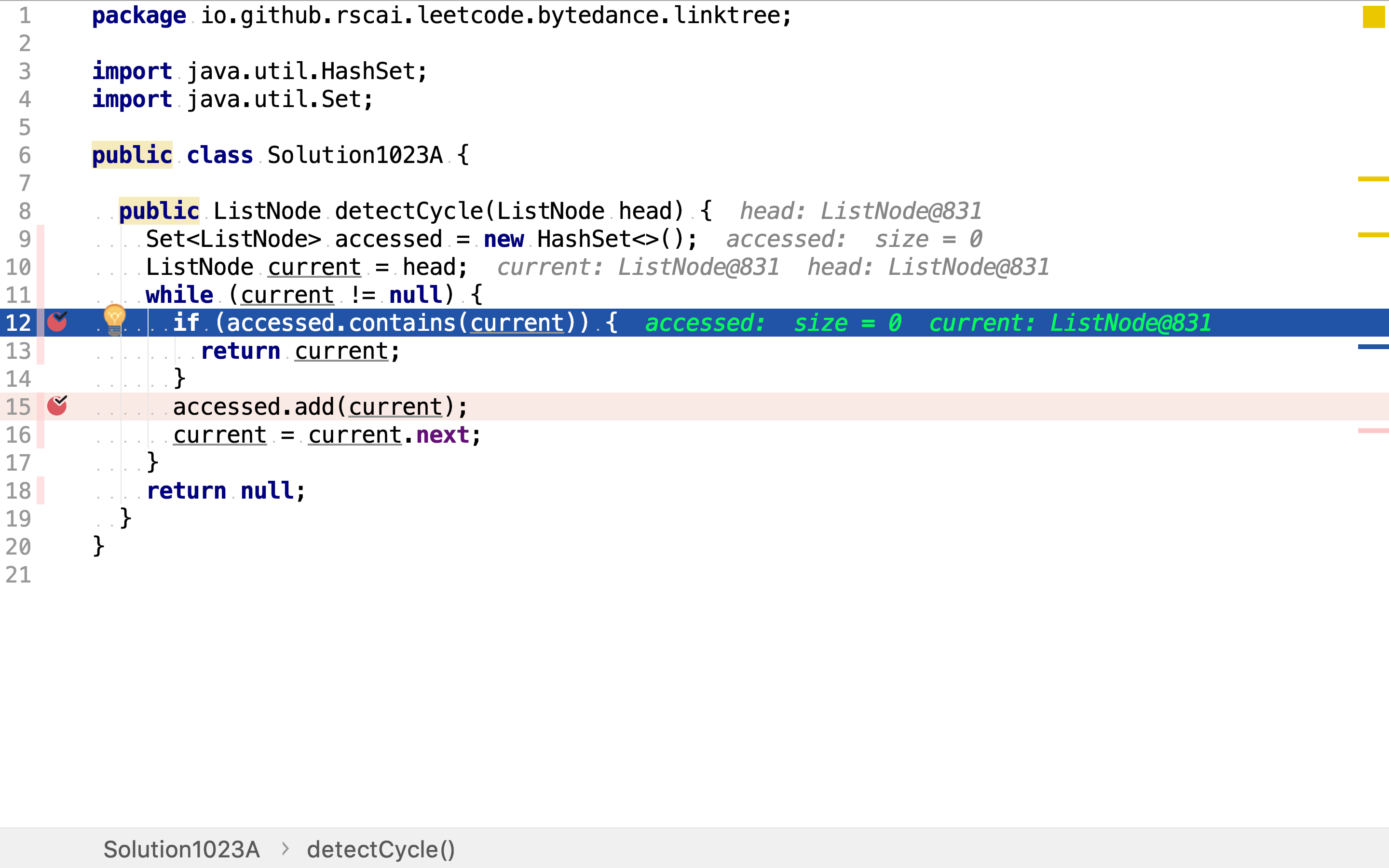
若不是,则记录其访问。
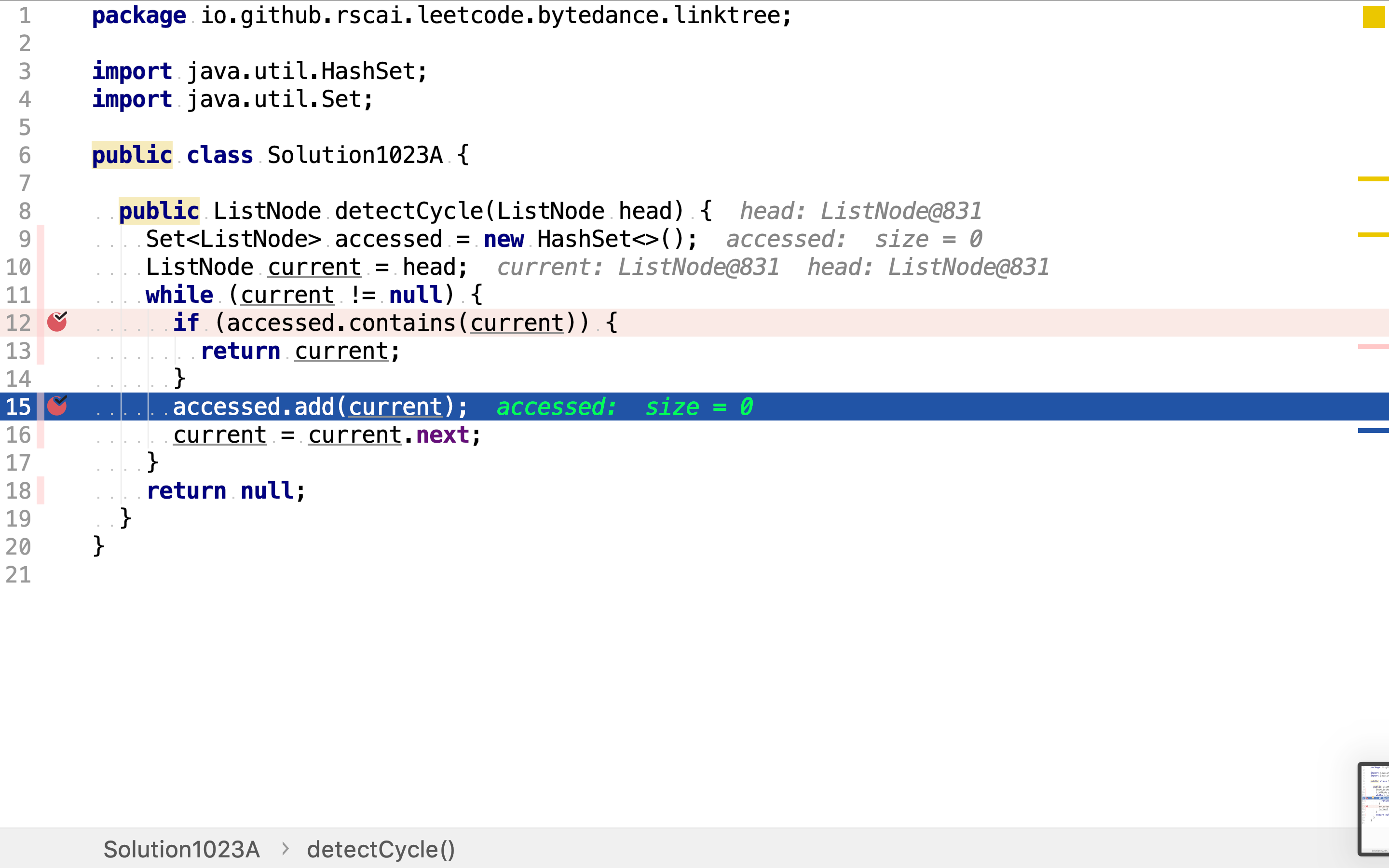
复杂度分析
时间复杂度
其只遍历了一遍链表,时间复杂度为。
空间复杂度
其要记录每个节点的访问记录,空间复杂度为。
Floyd's Tortoise and Hare
Floyd的循环寻找算法是一种指针算法,它只使用两个指针,它们以不同的速度在序列中移动。 它也被称为“乌龟和野兔算法”,暗指伊索寓言中的乌龟和野兔。
该算法的关键见解如下:如果存在环,则对于任何整数且,其中是要找到的环的长度,μ是环的第一个元素的索引。 基于此,当且仅当时,可以证明对于某些。 因此,该算法仅需要检查该特殊形式的重复值,即从序列的开始到另一个的两倍,以找到作为λ的倍数的重复的周期ν。 一旦找到ν,算法就从序列开始回溯序列,找到序列中的第一个重复值,使用λ除ν的事实,因此 。最后,一旦μ的值已知,它 通过搜索的第一位置,找到最短重复週期的长度λ是微不足道的。
因此,算法保持两个指向给定序列的指针,一个(乌龟)在,另一个(野兔)在。 在算法的每一步,它将i增加1,将龟向前移动一步,然后在序列中向前移动两步,然后比较这两个指针的序列值。 乌龟和野兔指向相等值的的最小值是期望值ν。
然后,分别从头和开始同步长移动。第一个交滙点就是入环点。
举个例子,给定如下链表:
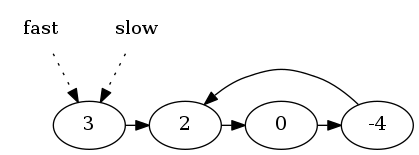
建立两个指针fast和slow,开始都指向头。fast以步长2向前移动,slow以步长1向前移动。
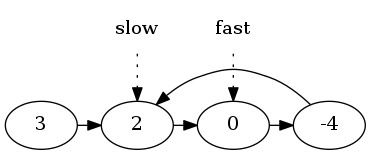
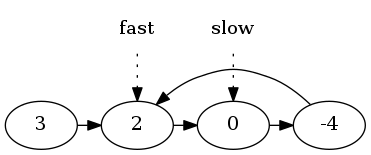

最终,它们在-4处相遇。此时:
- 指针移动了3次,
fast移动了步slow移动了步- 环长
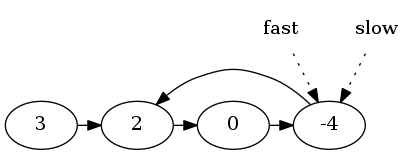
然后,创建两个指针head和v。分别以链表头和-4为起点,以1为步长,向后移到。
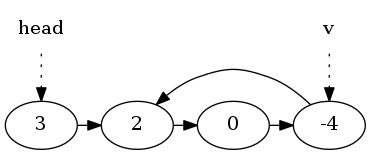
最终,它们相会与2。2即是环的入口点。
代码
package io.github.rscai.leetcode.bytedance.linktree;
/**
* Quick sort
*/
public class Solution1040B {
public ListNode sortList(ListNode head) {
return quickSort(head);
}
private ListNode quickSort(ListNode head) {
if (head == null) {
return head;
}
if (head.next == null) {
return head;
}
ListNode[] lists = divide(head);
ListNode first = lists[0];
ListNode pivot = lists[1];
ListNode second = lists[2];
ListNode sortedFirst = quickSort(first);
ListNode sortedSecond = quickSort(second);
ListNode sortedHead = sortedFirst;
ListNode sortedTail = sortedHead;
while (sortedTail != null && sortedTail.next != null) {
sortedTail = sortedTail.next;
}
if (sortedTail != null) {
sortedTail.next = pivot;
} else {
sortedHead = pivot;
sortedTail = pivot;
}
pivot.next = sortedSecond;
return sortedHead;
}
private ListNode[] divide(ListNode head) {
ListNode pivot = head;
ListNode firstHead = null;
ListNode firstTail = firstHead;
ListNode secondHead = null;
ListNode secondTail = secondHead;
ListNode current = head.next;
pivot.next = null;
while (current != null) {
ListNode next = current.next;
current.next = null;
if (current.val < pivot.val) {
if (firstTail == null) {
firstTail = current;
firstHead = firstTail;
} else {
firstTail.next = current;
firstTail = firstTail.next;
}
} else {
if (secondTail == null) {
secondTail = current;
secondHead = secondTail;
} else {
secondTail.next = current;
secondTail = secondTail.next;
}
}
current = next;
}
return new ListNode[]{firstHead, pivot, secondHead};
}
}
首先,使用fast和slow两个步长分别为2和1的指针找出位置v。
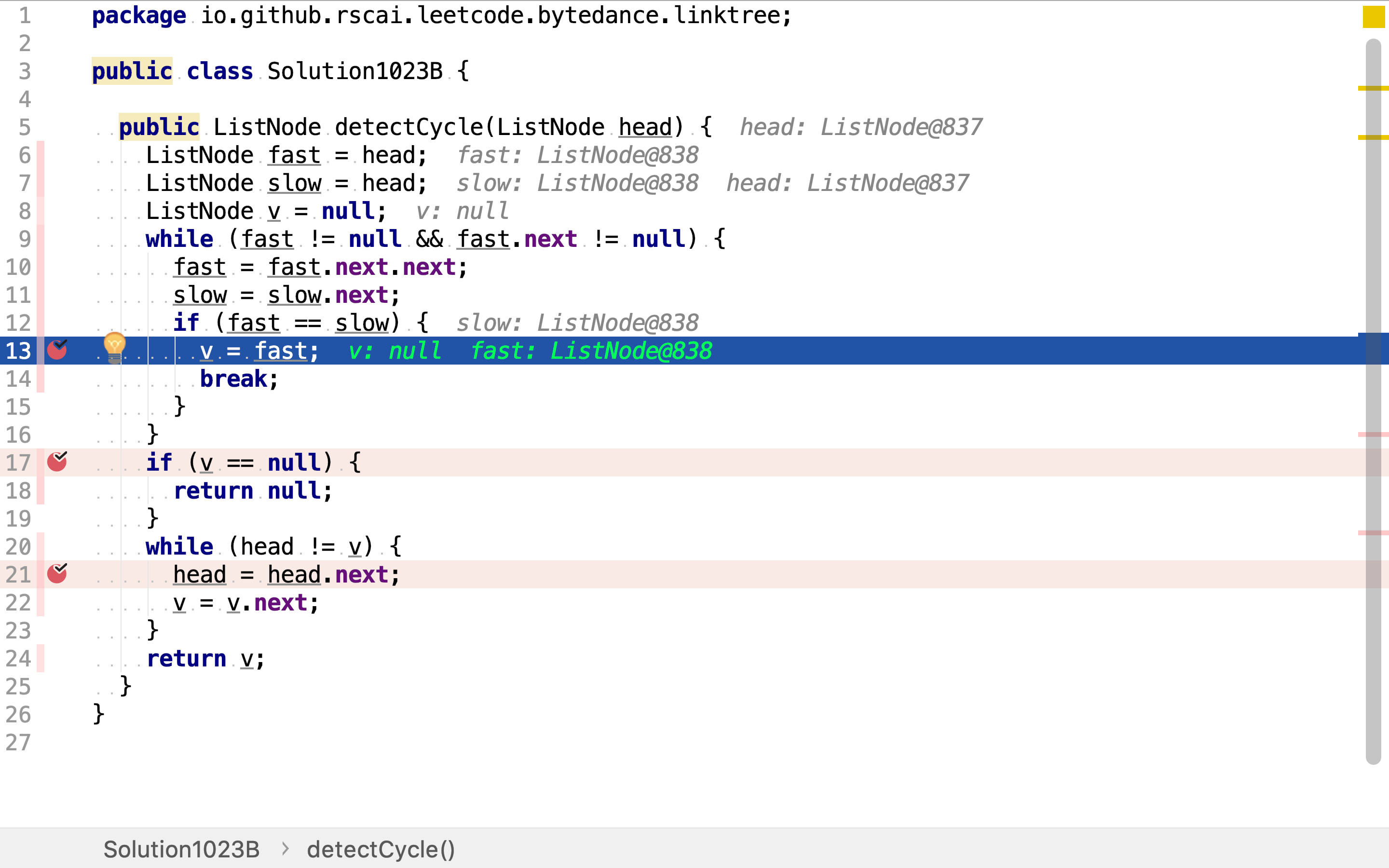
若fast和slow没有交会,则说明链表中不存在环。
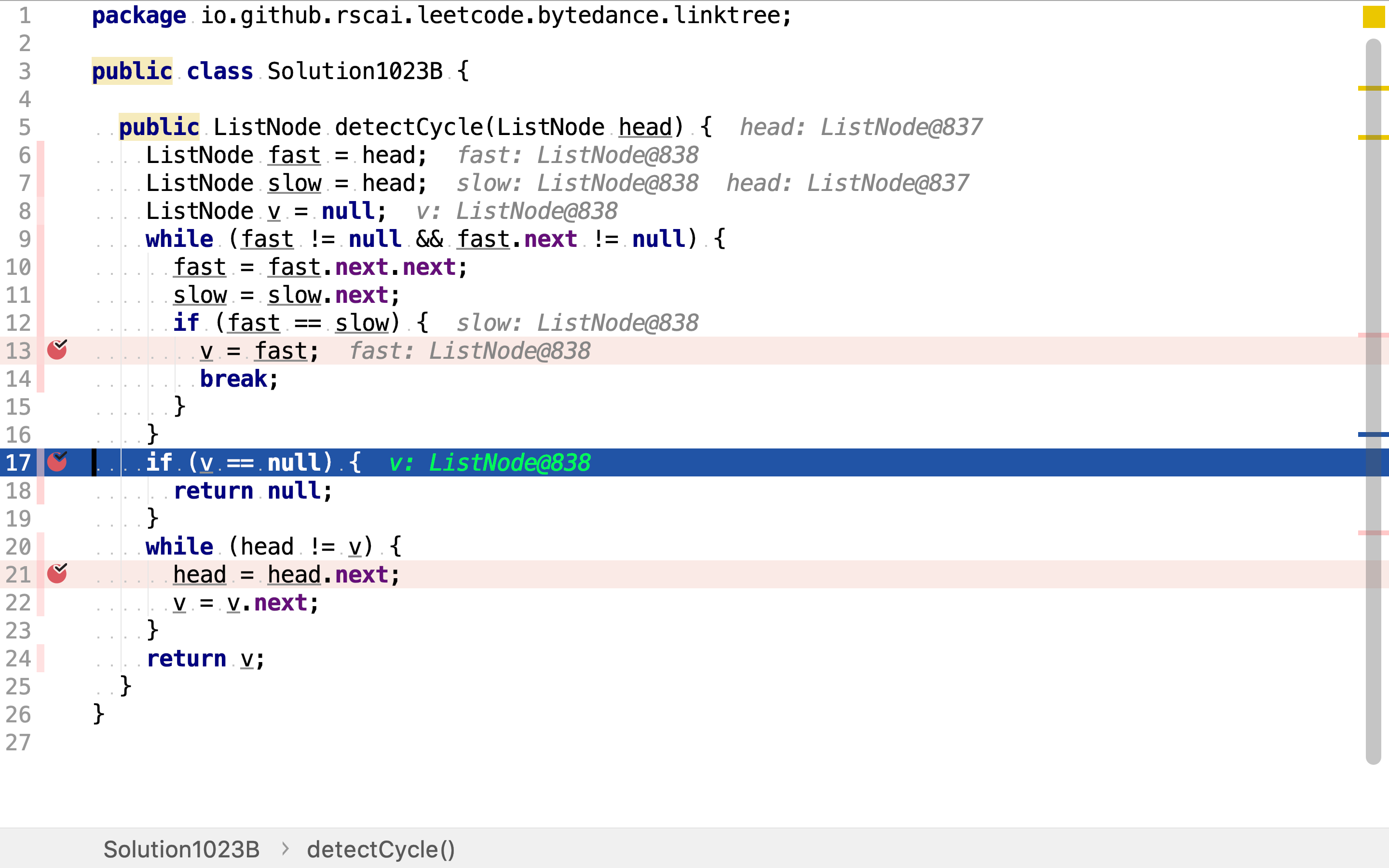
若fast和slow最终交会,则从交会点和头分别出发,以步长1向后遍历链表。最终交会点即是环入口点。
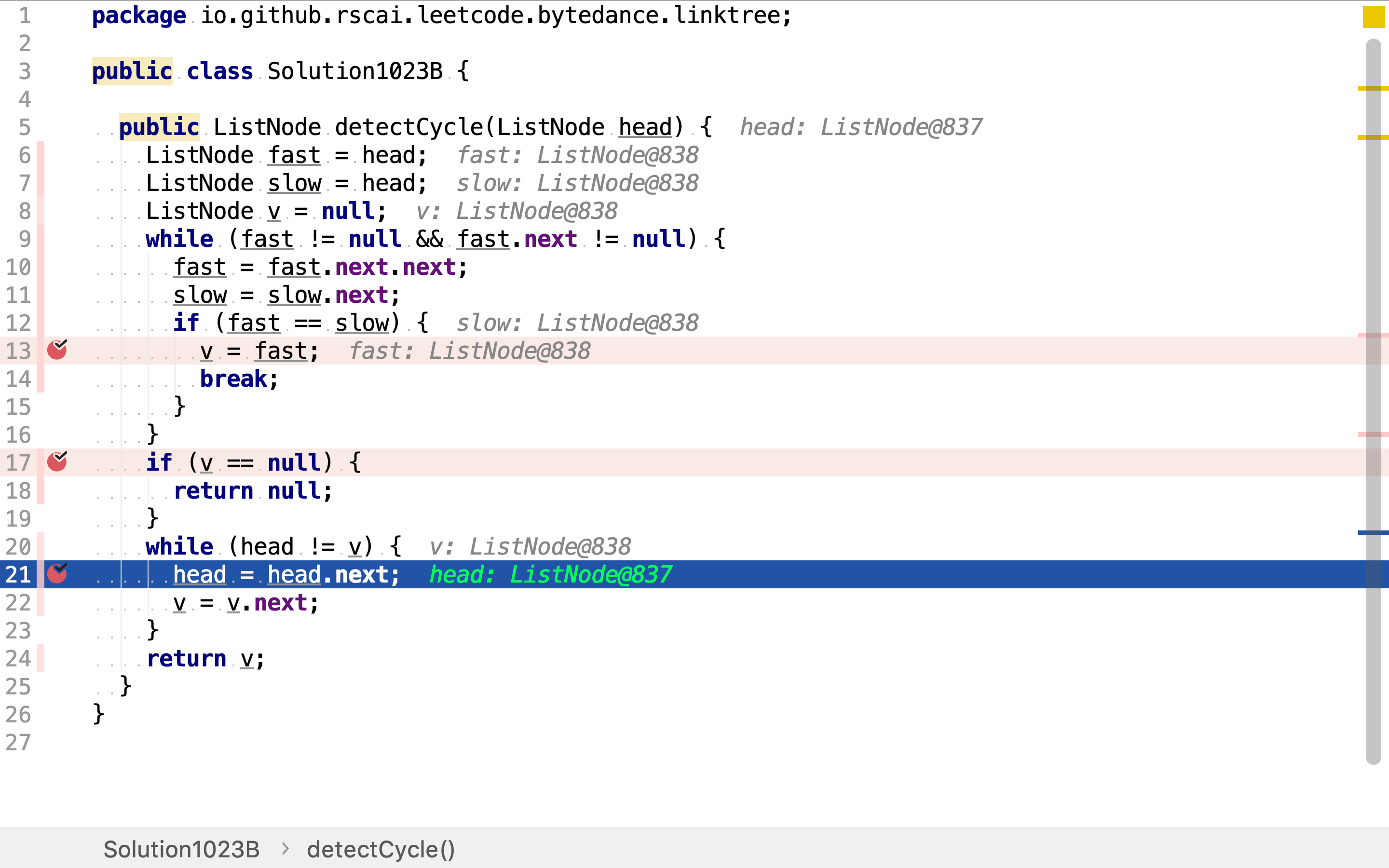
复杂度分析
时间复杂度
其仅遍历了链表k次(k是常数),所以时间复杂度为。
空间复杂度
使用了三个变量fast、slow和v。空间复杂度为。
参考
















