合併区间

题目

给出一个区间的集合，请合併所有重叠的区间。

示例 1：

输入: [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合併为 [1,6].

示例 2：

输入: [[1,4],[4,5]]
输出: [[1,5]]
解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。

图连通分量法

连通分量

在图论中，元件又称为连通元件、分量、或分支，是一个无向子图，在元件中的任何两个顶点都可以经由该图上的边抵达另一个顶点，且没有任何一边可以连到其他子图的顶点。

演算法

一种直接了当的以线性时间（以图的顶点和边数量计）计算图连通分量的方法是使用广度优先搜寻或深度优先搜寻。在任何一种情况下，从某个顶点v开始的搜索将会返回包含v的完整连通分量。要找到图的所有连通分量，只需遍历每一个顶点，以每一个顶点为起点开始广度优先或深度优先搜寻。Hopcroft和Tarjan（1973）基本上描述了这种算法，并指出在那时它是“众所周知的”。

如果将每个区间视为图中的一个点，将两个区间重叠视为图中两个相邻，则所有重叠的区间集合即为图中的连通分量。

举个例子，给定区间集合[[1,6],[4,7],[6,11],[13,16],[16,24]]。该区间集合可建模为如下图：

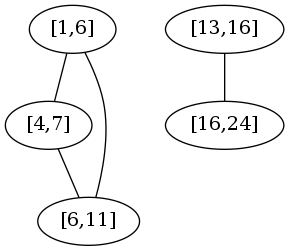
集合中五个区间映射为图中的五个点。其中：

• 区间[1,6], [4,7], [6,11]相互重叠即相邻
• 区间[13,16]和[16,24]相互重叠即相邻

使用深度优先搜寻法查找所有连通分量：

• 以[1,6]为起点深度优先遍历图，得到连通分量[[1,6], [4,7], [6,11]]，同时记录下已访问的点。

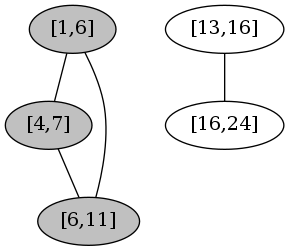
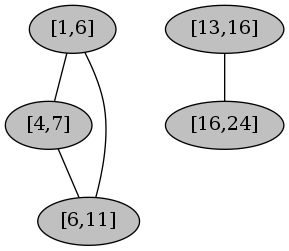
• 以[13,16]为起点深度优先遍历图，得到连通分量[13,16], [16,24]]，同时记录已访问过的点。

代码实现

以每一个区间为起点，使用深度优先搜寻法遍历图搜寻连通分量。

保留下非空的连通分量。

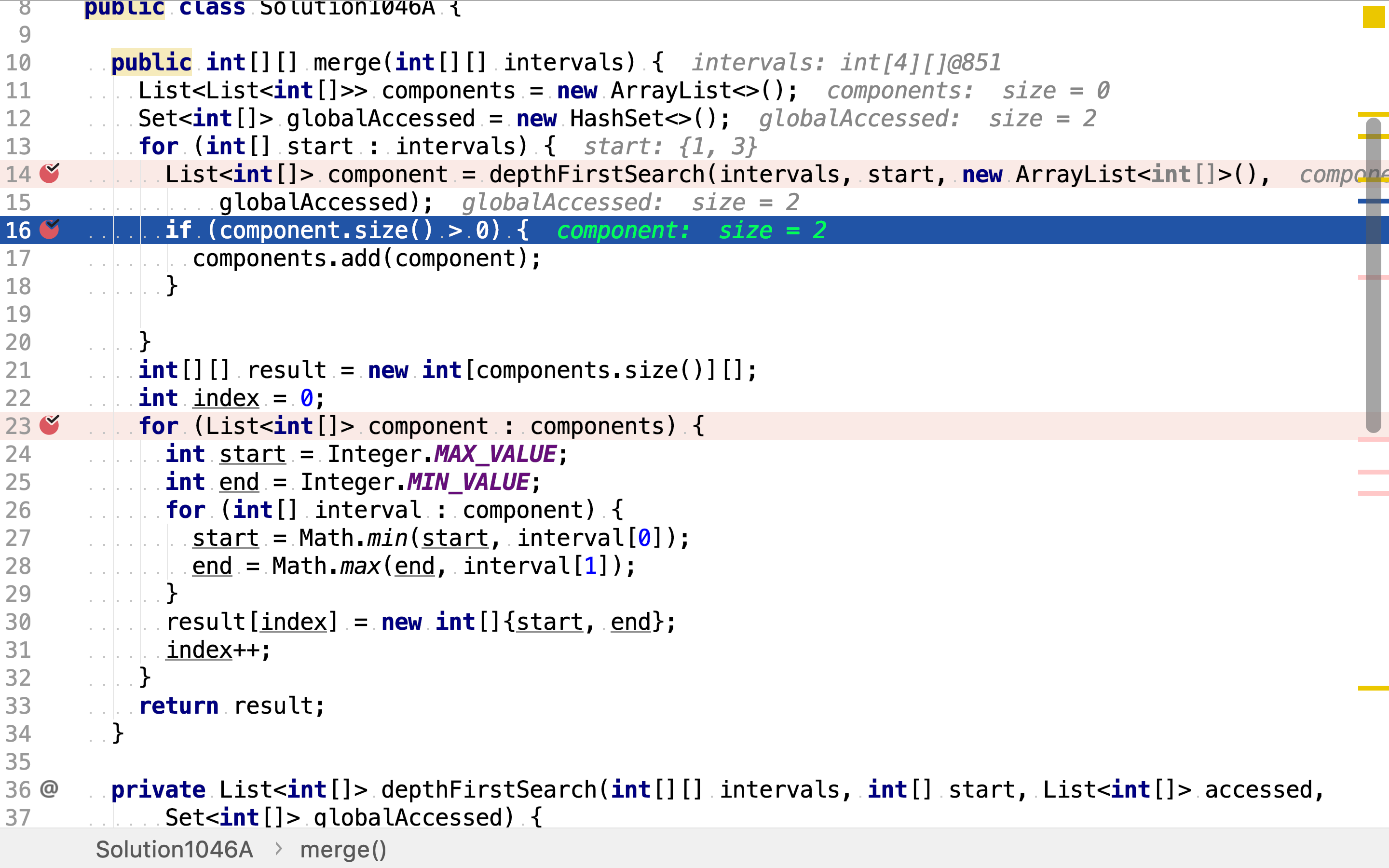
最后，各自合併连通分量𥚃的点即区间。

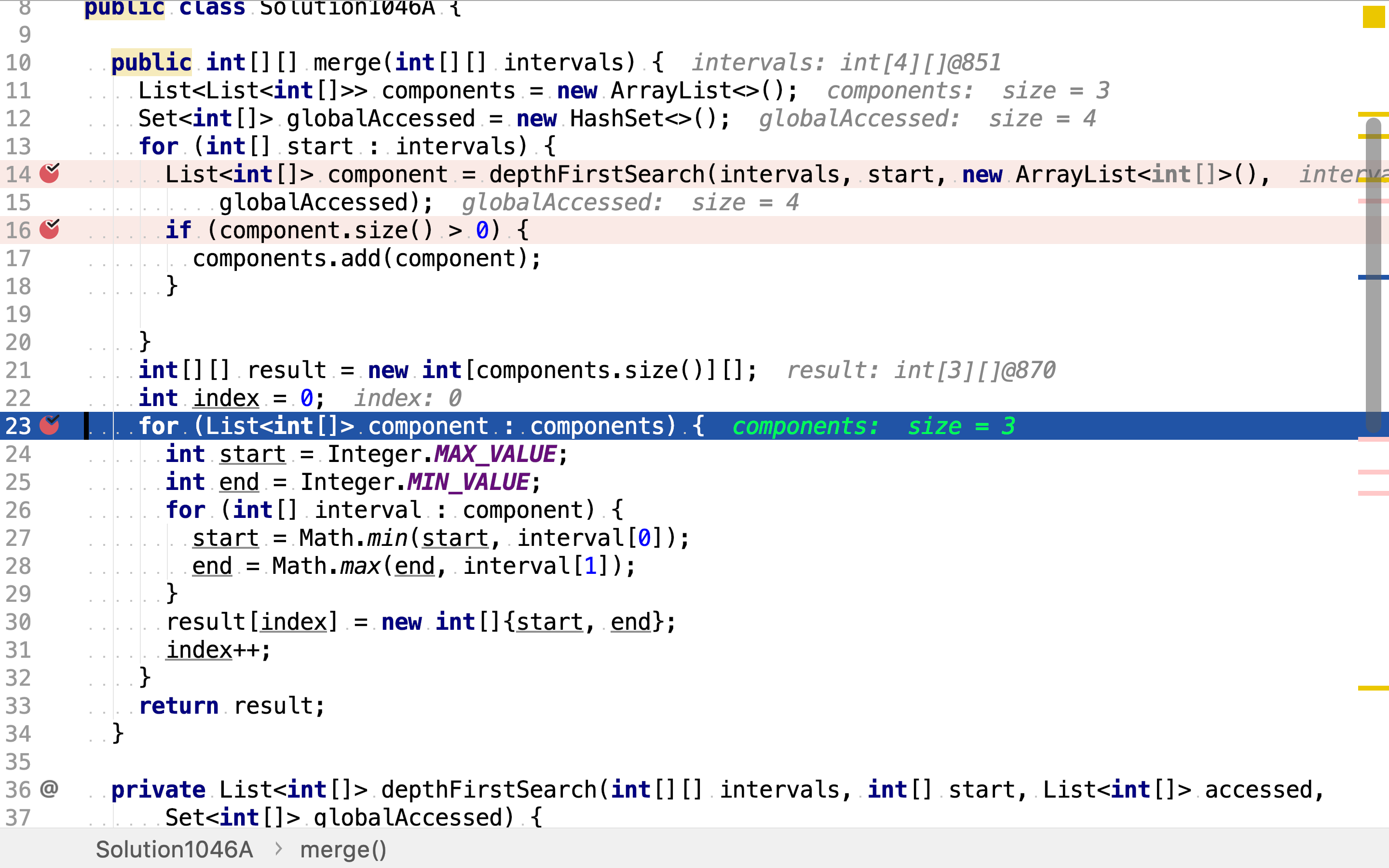
其中，深度优先搜寻法以递归方式实现。首先，访问当点（即区间），将其加入「全局已访问集合」；然后，获取与起点相邻但未被访问的点，以该点为新的起点进行深度优先搜寻；再然后，获取下一个与起点相邻但未被访问的点，以该点为新的起点进行深度优先搜寻；递归终止条件为「没有相邻但未被访问的点」。

首先，判断起点是否已被访问过。

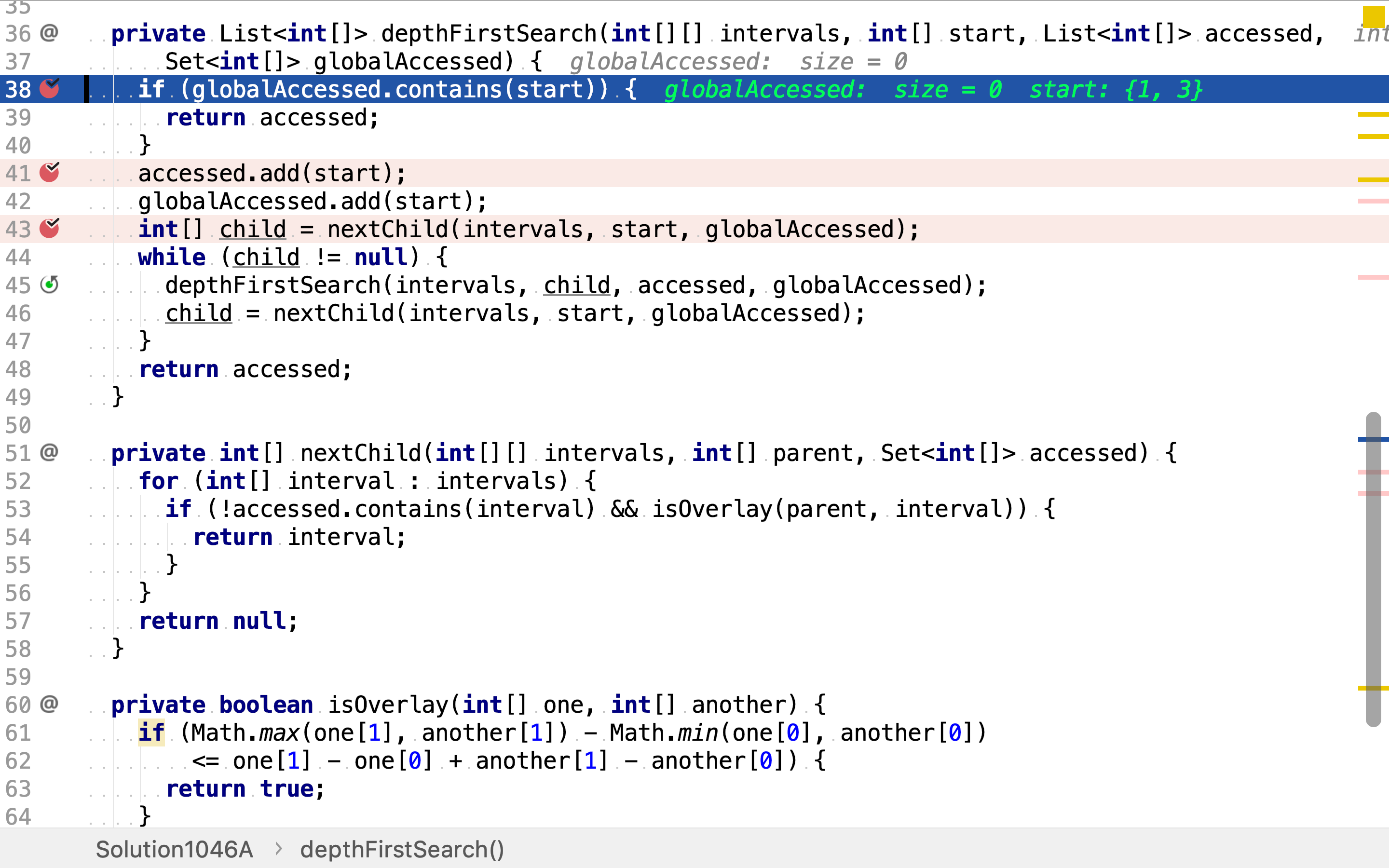
若否，则将其纳入当前连通分量中，并记录到「全局已访问」点集中。

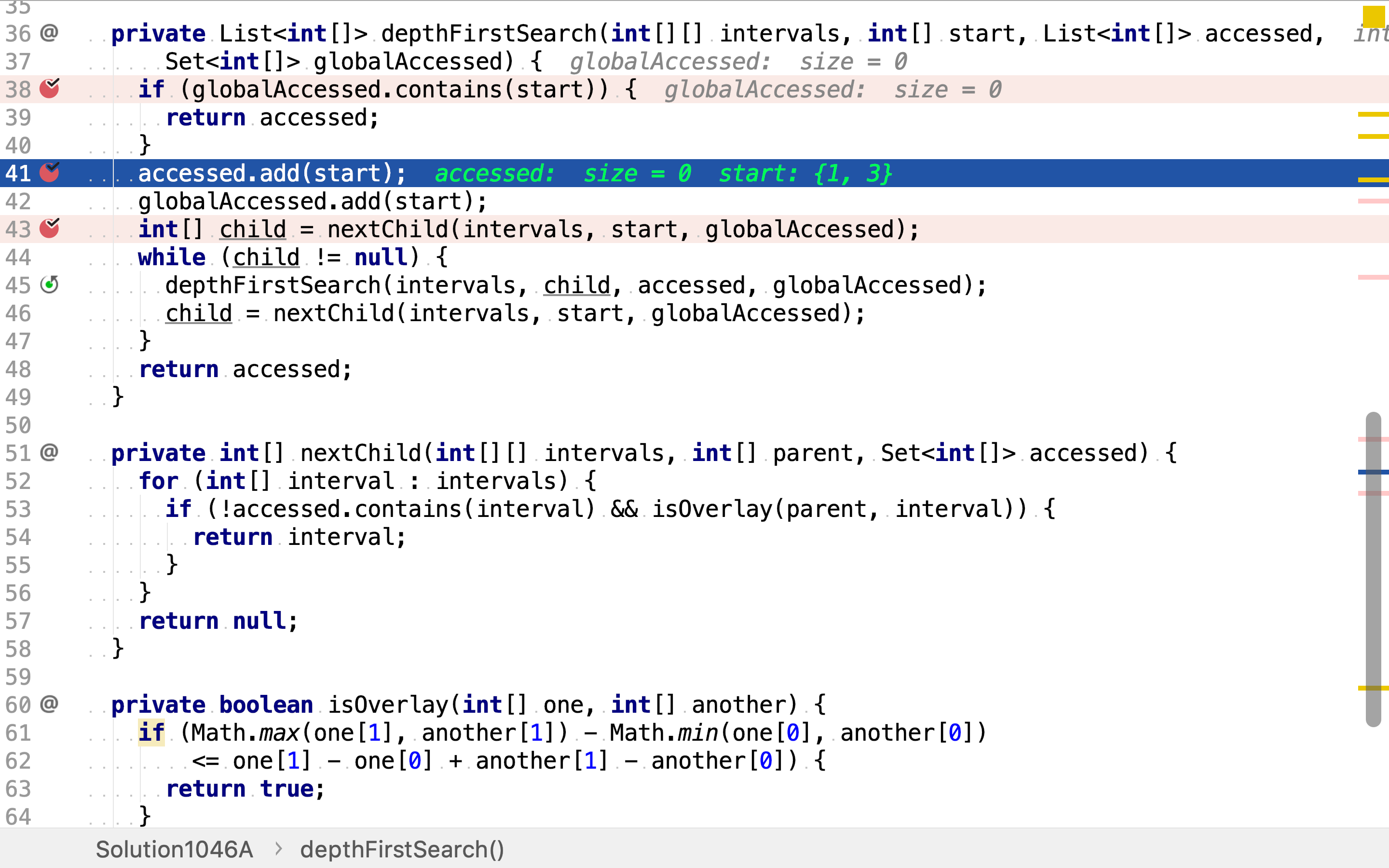
然后，获取下一个相邻但未访问过的点，以该点为新的起点，递归套用depthFirstSearch。

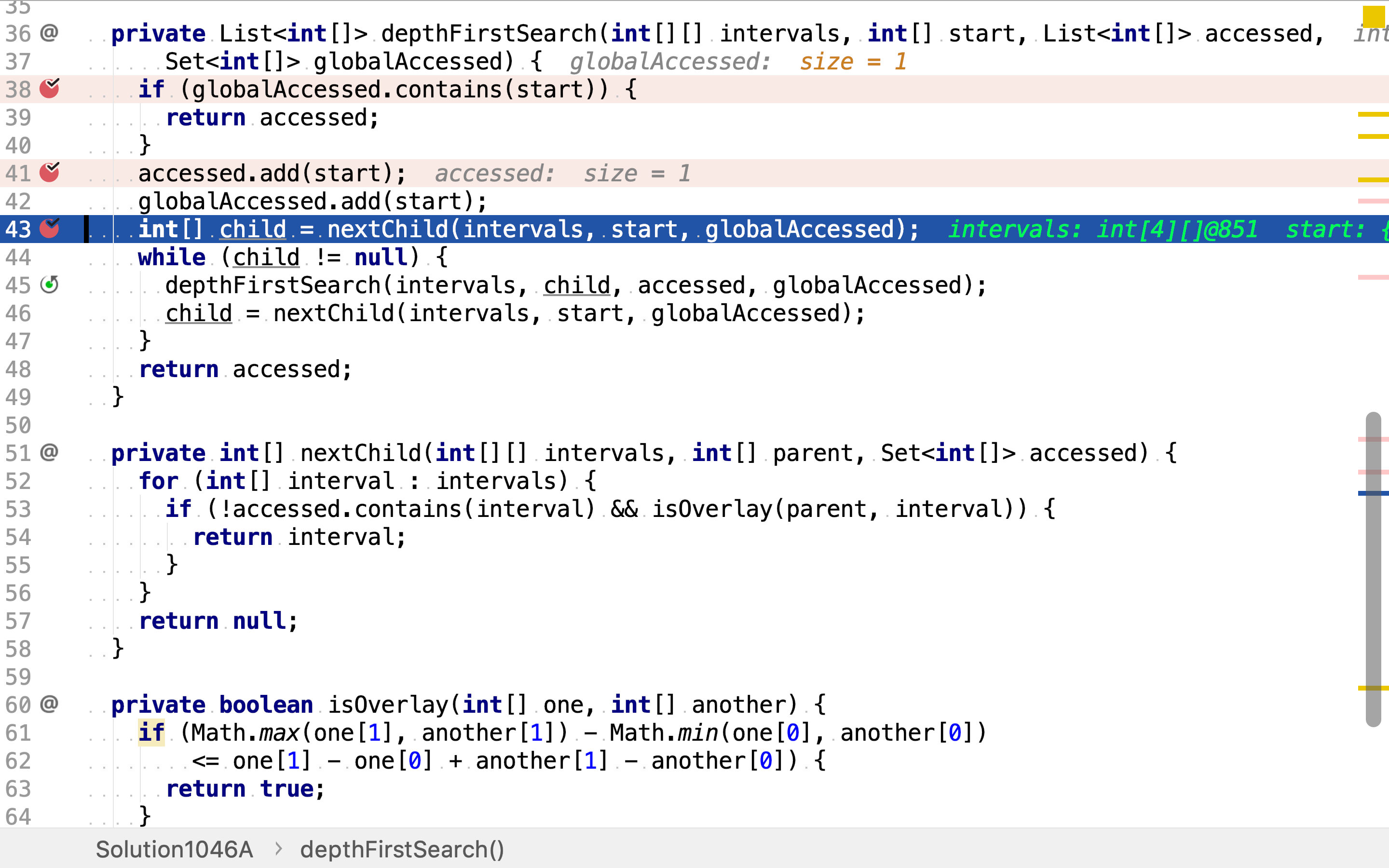
递归终止条件为：没有未访问的相邻点（重叠的区间）。

复杂度分析

时间复杂度

首先，其针对每一个点都进行一次深度优先搜寻和集合比较。但depthFirstSearch会将访问过的点都记录下来，以避免重复访问。所以，假设输入区间数为$n$，这一段的时间复杂度为$\mathcal{O}(n)$。

    for (int[] start : intervals) {
      List<int[]> component = depthFirstSearch(intervals, start, new ArrayList<int[]>(),
          globalAccessed);
      if (component.size() > 0) {
        components.add(component);
      }
    }

然后，各自合併连通分量时，两重循环要遍历每一个原输入区间。时间复杂度为$\mathcal{O}(n)$。

    for (Set<int[]> component : components) {
      int start = Integer.MAX_VALUE;
      int end = Integer.MIN_VALUE;
      for (int[] interval : component) {
        start = Math.min(start, interval[0]);
        end = Math.max(end, interval[1]);
      }
      result[index] = new int[]{start, end};
      index++;
    }

将所有的加起点，时间复杂度为

$$\begin{aligned} C_{time} &= \mathcal{O}(n) + \mathcal{O}(n) \\ &= \mathcal{O}(n) \end{aligned}$$ 。

空间复杂度

使用了三个变量components, globalAccessed和result。空间复杂度为：

$$\begin{aligned} C_{space} &= \mathcal{O}(n + n + n) \\ &=\mathcal{O}(n) \end{aligned}$$

排序

如果给定的区间是按起始点从小到大排序的，则重叠的区间一定是连续的。所以，将区间按起始点从小到大排序；然后，一次遍历区间，将重叠的连续区间合併。

举个例子，给定区间[[1,6],[4,7],[6,11],[13,16],[16,24]]。按起始点升序排序后得到[[1,6],[4,7],[6,11],[13,16],[16,24]]

• [1,6]和[4,7]重叠，合併为[1,7]

• [1,7]和[6,11]重叠，合併为[1,11]

• [1,11]和[13,16]不重叠
• [13,16]和[16,24]重叠，合併为[13,24]

从以上例子可以看出，本演算法基于以下命题不成立：

在有序的区间序列中，存在三个连序的区间a, b和c。若a和c重叠，则a和b不重叠且b和c不重叠。

证明

设：

• 区间$a$的起止点分别为$a_s, a_s$
• 区间$b$的起止点分别为$b_s, b_e$
• 区间$c$的起止点分别为$c_s, c_e$

已知：

• a, b, c 是按起始点从小到到排序，即$a_s \leq b_s \leq e_s$
• a和c重叠，即$c_s \leq a_e$

则：

$$(b_s \leq c_s, c_s \leq a_e) \to bs \leq a_e$$

$$(b_s \leq a_e, a_s \leq b_s) \to a和b重叠$$

所以，命题不成立。

代码实现

首先，使用JDK提供的Arrays.sort对输入区间序列排序。

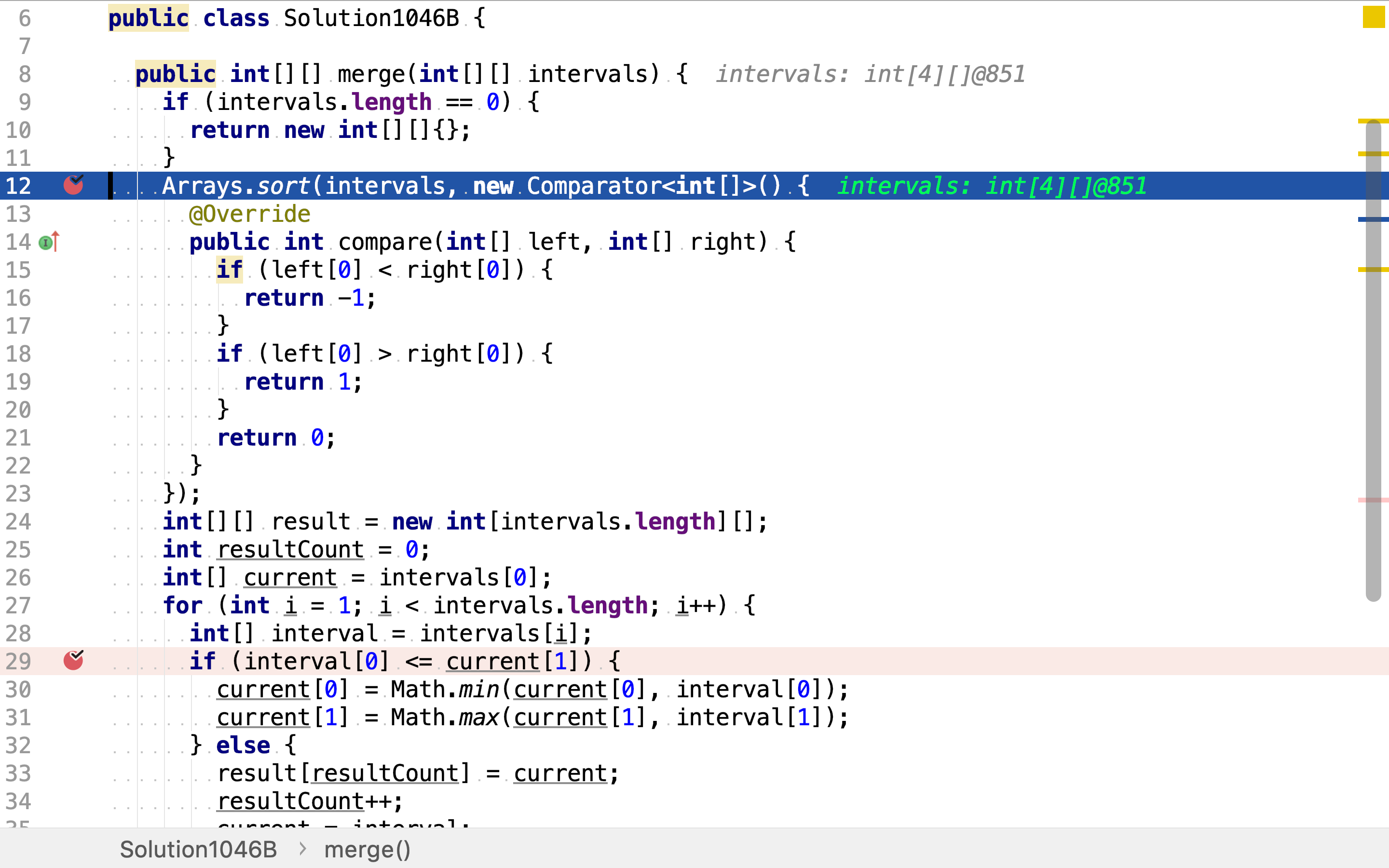
然后，再合併相邻且重叠的区间。

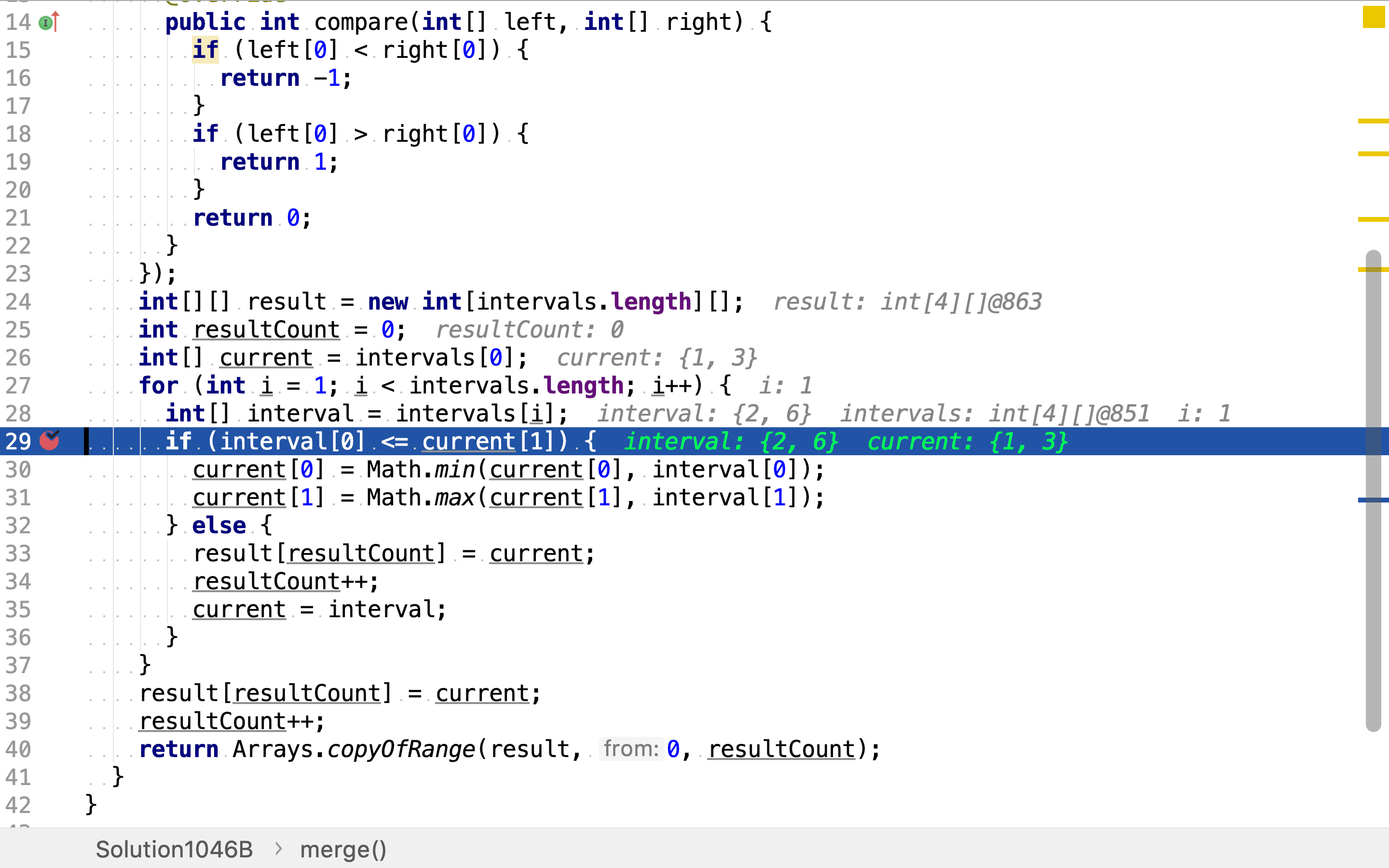
复杂度分析

时间复杂度

Arrays.sort实现了「合併排序（Merge Sort）」，时间复杂度是$n \log(n)$。然后再遍历了一次有序区间序列。所以，整体时间复杂度为：

$$\begin{aligned} C_{time} &= \mathcal{O}(n \log(n) + n) \\ &= \mathcal{O}(n \log(n)) \end{aligned}$$

空间复杂度

使用了变量result，空间复杂度为$\mathcal{O}(n)$。