买卖股票的最佳时机

题目

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。

注意你不能在买入股票前卖出股票。

示例 1:
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
    注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
示例 2:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

穷举法

买卖有一买一卖组成，卖出价与买入价之间的差值即为利润。穷举法就是罗列所有买入价和卖出价之间的组合，再算出利润，取其中最大的利润。

举个例子，给定价格序列[7,1,5,3,6,4]。买入价有六种选择。用树表示就是第1层（根节点为第0层）有六个子节点。卖出价的选则受买入点影响。比如，当在第一天买入时，可选的卖出点只能是第二天及以后；当在第二天买入时，可选的卖出点只能是第三天及以后；以此类推。

代码

package io.github.rscai.leetcode.bytedance.dynamic; public class Solution1042A { public int maxProfit(int[] prices) { int maxProfit = 0; for (int buyAt = 0; buyAt < prices.length; buyAt++) { for (int sellAt = buyAt + 1; sellAt < prices.length; sellAt++) { int profit = prices[sellAt] - prices[buyAt]; if (profit > maxProfit) { maxProfit = profit; } } } return maxProfit; } }

首先，选取买入价。任意一个价格都可以作为买价。使用for loop遍历所有价格作为买入价。

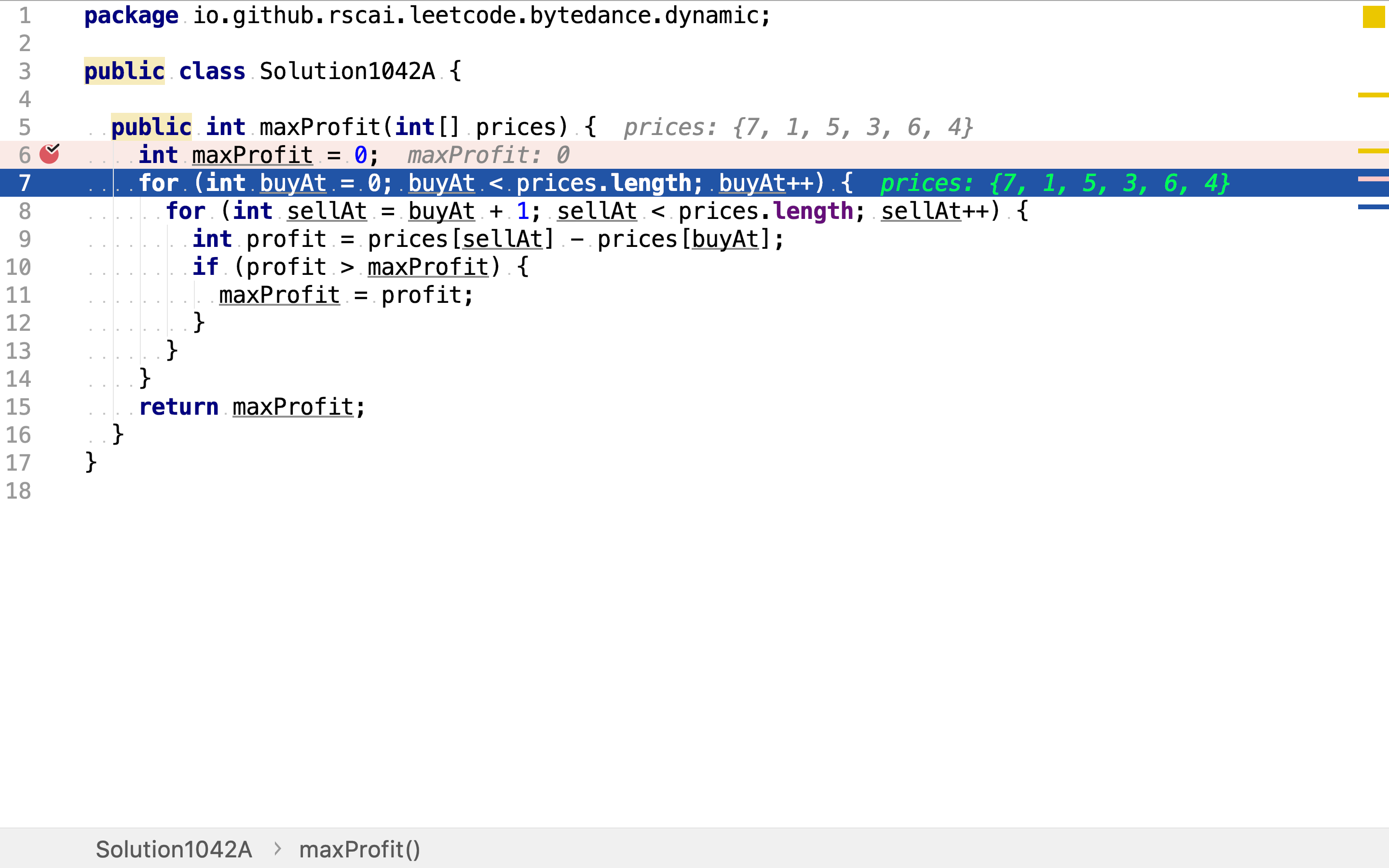
卖出动作必需要在买入之后，所以针对不同的买入点，可选的买出点是不同的。比如，当买入点为第一天，则只能在第二天及以后的某一卖出。使用for loop遍历买入点之后的每一天。两层for loop就罗列出了所有的买入/卖出组合，再计算每一个买入/卖出组合产成的利润，留下最大的即是所有求解。

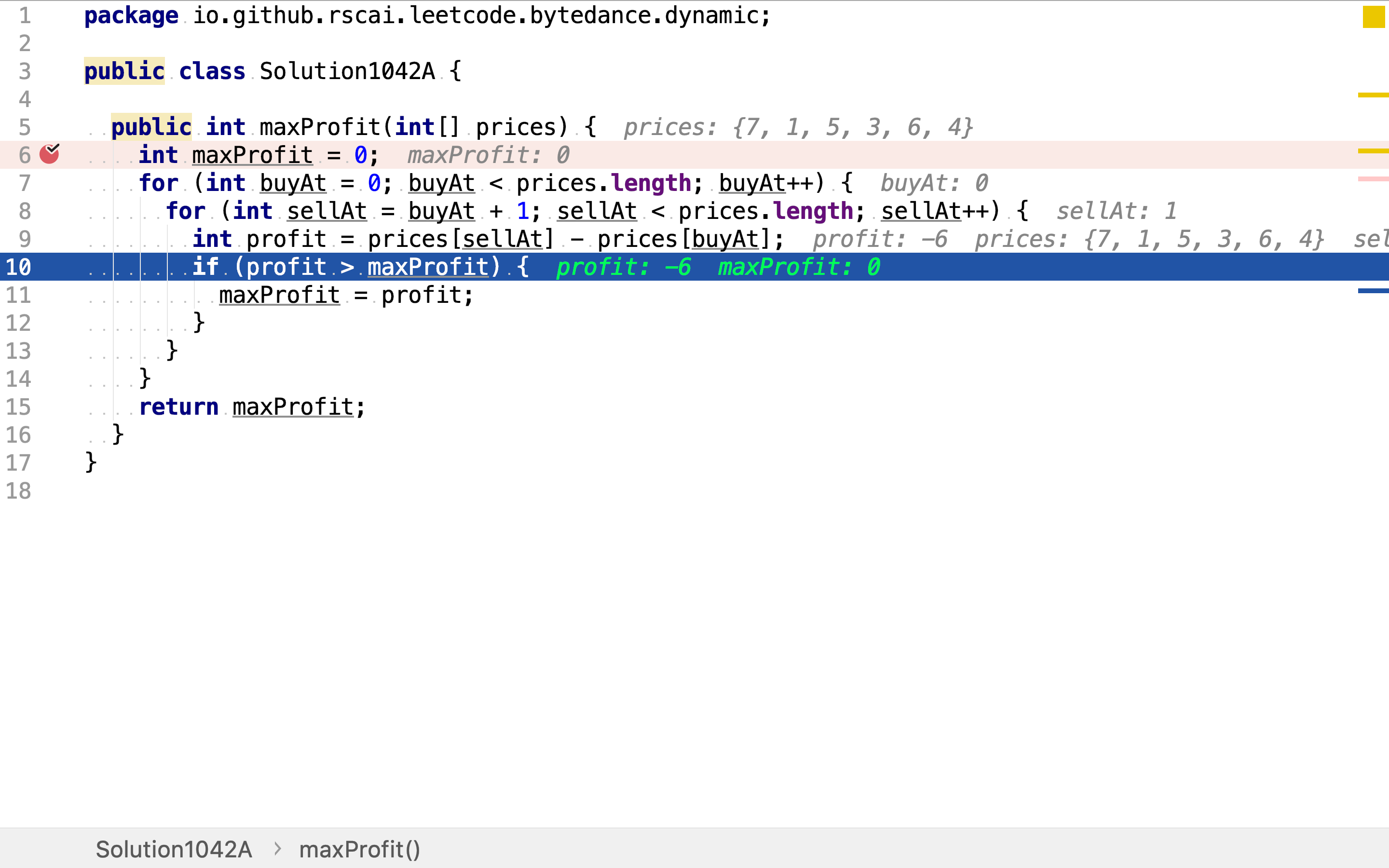
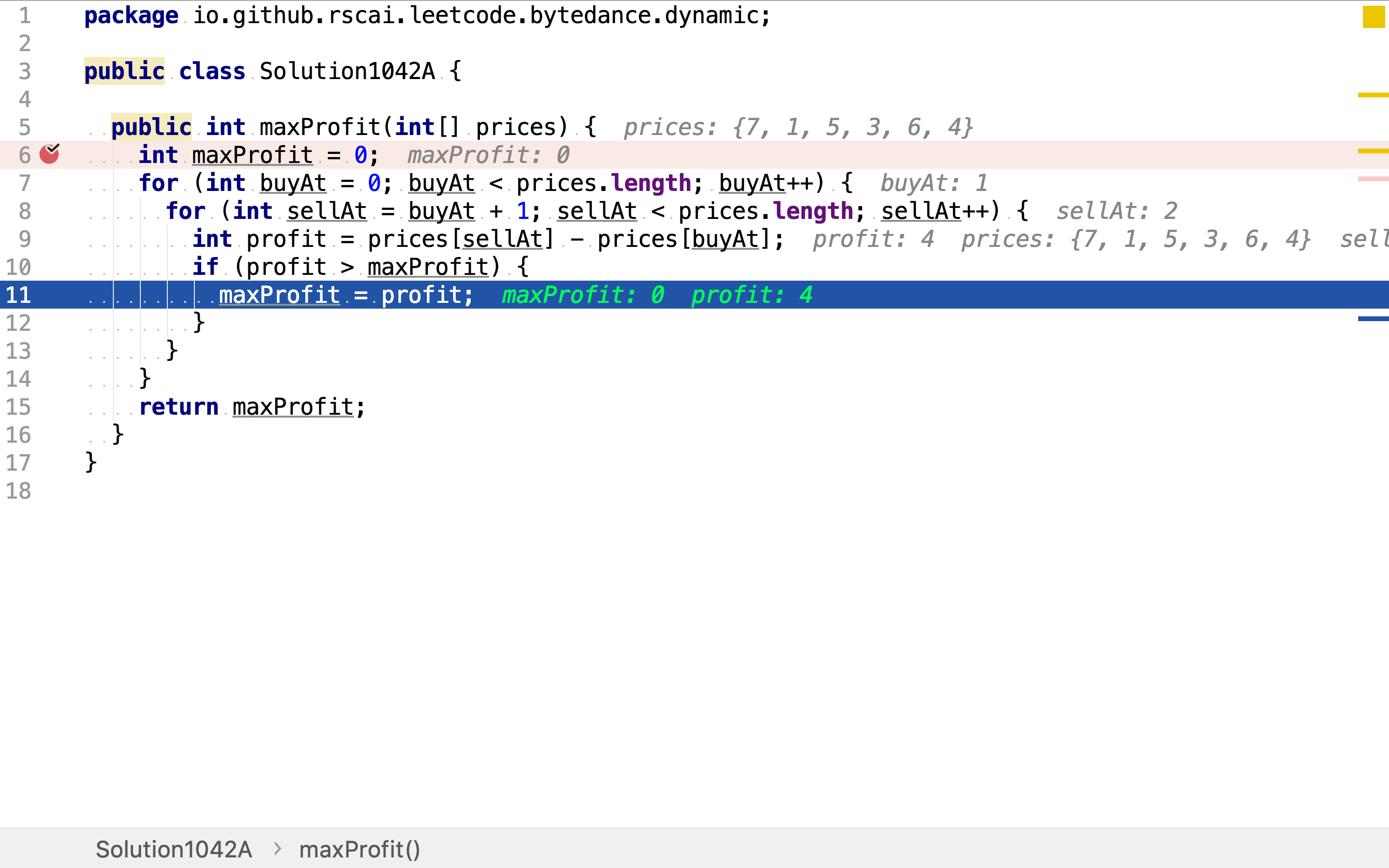
复杂度分析

时间复杂度

两层for loop共产生了 $\frac{n(n-1)}{2}$ 次循环。时间复杂度为

$\begin{aligned} C_{time} &= \mathcal{O}(\frac{n(n-1)}{2}) \\ &= \mathcal{O}(n^2) \end{aligned}$

空间复杂度

只使用了两个变量maxProfit和profit。空间复杂度为

$\begin{aligned} C_{space} &= \mathcal{O}(2) \\ &= \mathcal{O}(1) \end{aligned}$

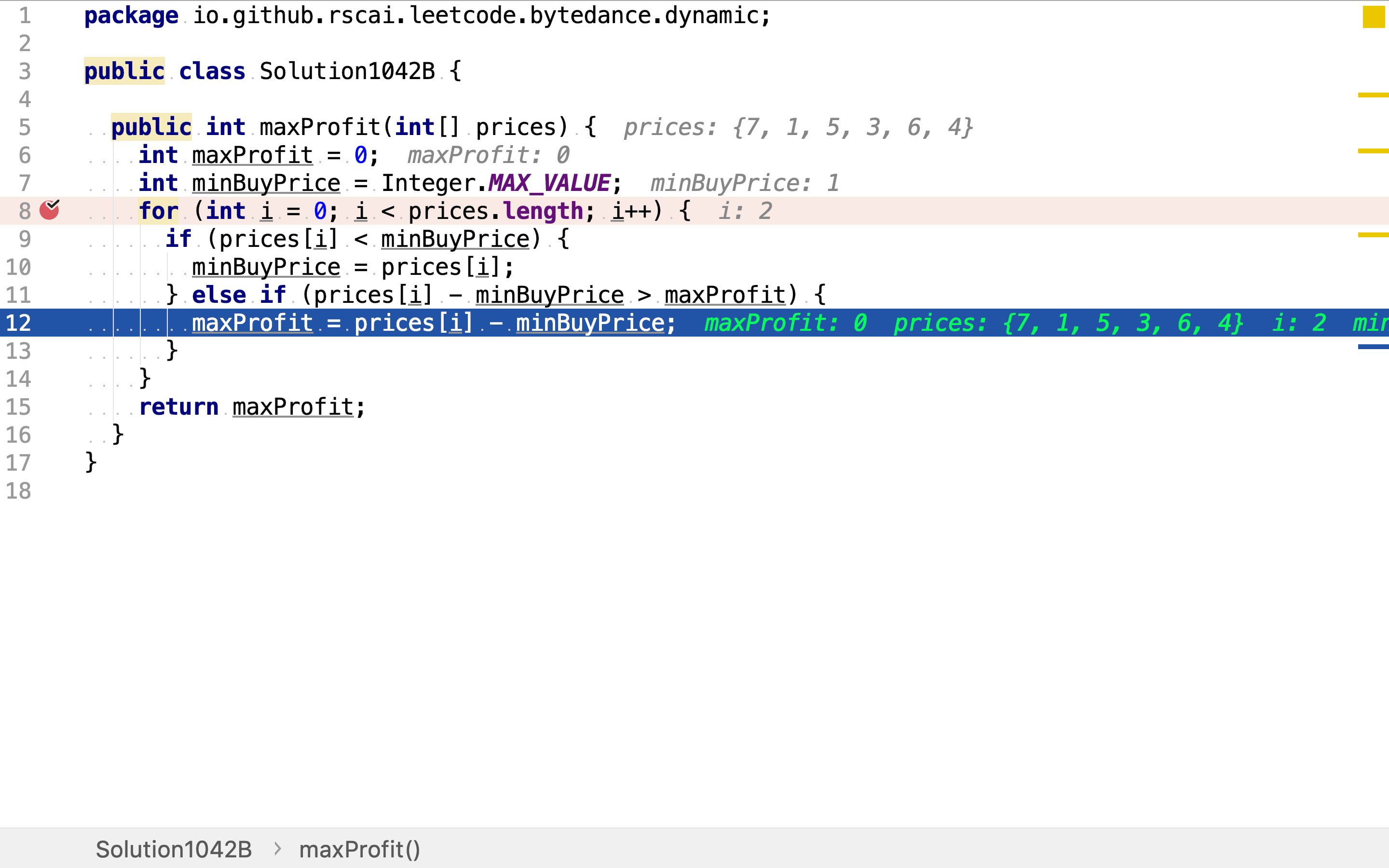
一次遍历

假设有两个买卖组合 $(buy_a, sell_a)$ 和 $(buy_b, sell_b)$ ，如果 $sell_a = sell_b$ 且 $buy_a > buy_b$ ，则利润 $sell_b - buy_b > sell_a - buy_a$ 。所以可以直接排除买入价大于之前买入价的组合。以树表示，就是如果第二层节点的值（买入价）大于同层左边任一节点的值，则以其为买入点的组合产生的利润绝不会是最大利润。（其左边的节点的子节点值的集合包含了右边节点的子节点值的集合。）

再来看第二层「卖出价」。如果卖出价比卖入价小，则其利润为负，且该值价以买入价的身份出现在第一层。且后续值都会以另一个更小的买入的卖出价出现。比如，以7为买入价，卖出价选择有[1, 5, 3, 6, 4]。卖出价1比买入价7小，则后续[5, 3, 6, 4]会以卖出价出现在以1为买入价的组合中。「当卖出价相等时，买入价小的组合其利润一定大于买入价大的组合。」所以，就无需计算后续以7为买入价的组合了。

可以看出，每个值都只被访问了一次。所以，两层循环可以合併成一层循环。

代码

package io.github.rscai.leetcode.bytedance.dynamic; public class Solution1042B { public int maxProfit(int[] prices) { int maxProfit = 0; int minBuyPrice = Integer.MAX_VALUE; for (int i = 0; i < prices.length; i++) { if (prices[i] < minBuyPrice) { minBuyPrice = prices[i]; } else if (prices[i] - minBuyPrice > maxProfit) { maxProfit = prices[i] - minBuyPrice; } } return maxProfit; } }

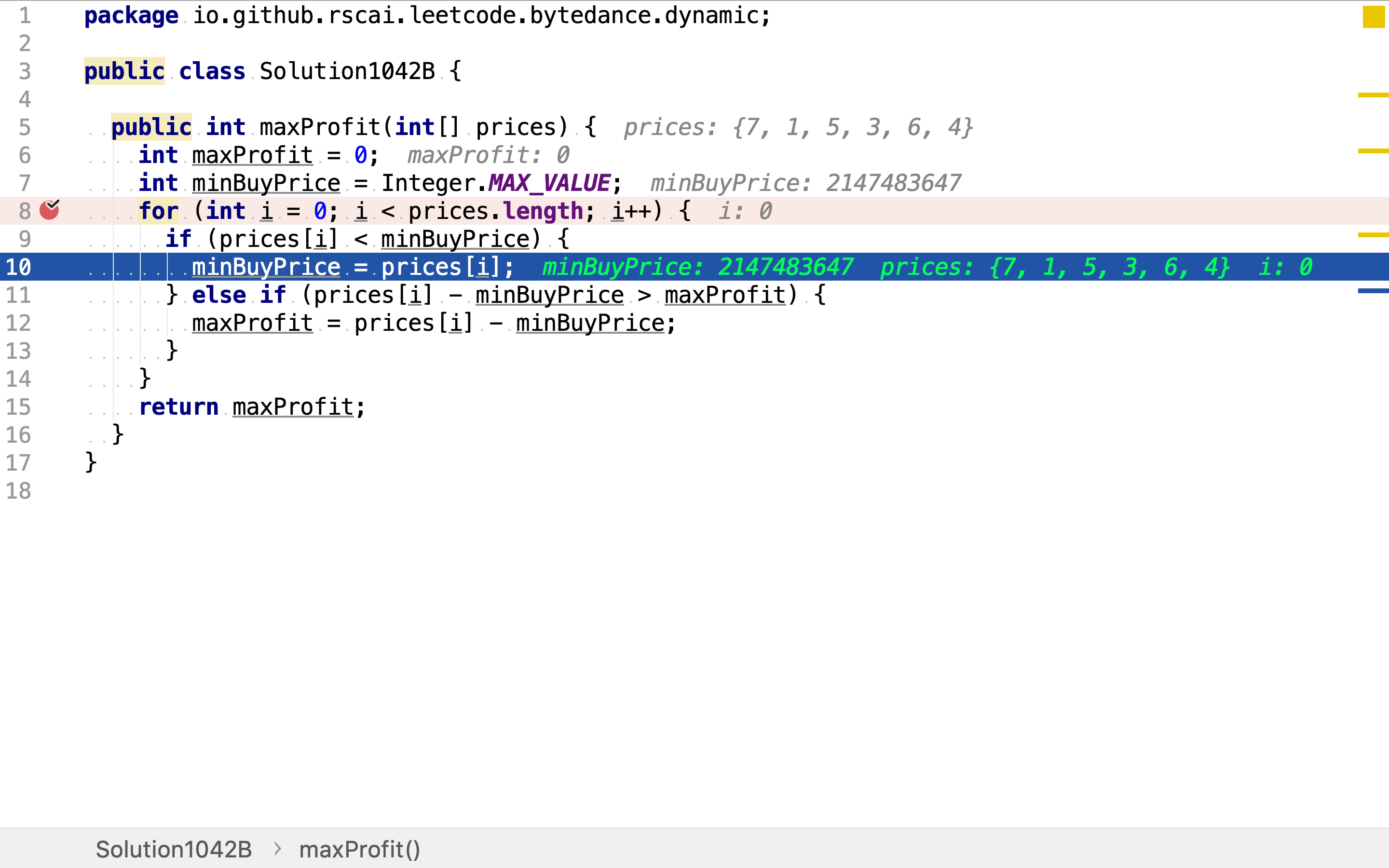
用一次for loop遍历所有价格。同时寻找目前为止最低价和最大利润。

若最低价在最高价之间出现的情况下，当遍历到最高价时，minBuyPrice保存的是最低价。计算出来的价差就是最大利润。

若最低价出现在最高价之后，则当遍历到最高价时，minBuyPrice保存的是最高之前的局部最低价；当遍历到最低价之后的局部最高价时，minBuyPrice保存的是全局最低价。

所以，一次for loop一定遍历了三个必然包含最大利润的组合，再从中取出最大值即为全局最大利润。