搜索旋转排序数组
题目
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
(例如,数组
[0,1,2,4,5,6,7]可能变为[4,5,6,7,0,1,2])。搜索一个给定的目标值,如果数组中存在这个目标值,则返回它的索引,否则返回
-1。你可以假设数组中不存在重复的元素。
你的算法时间复杂度必须是 O(log n) 级别。
示例1:
输入: nums = [4,5,6,7,0,1,2], target = 0 输出: 4示例2:
输入: nums = [4,5,6,7,0,1,2], target = 3 输出: -1
二分搜寻法
在电脑科学中,二分搜寻(英语:binary search),也称折半搜寻(英语:half-interval search)、对数搜寻(英语:logarithmic search),是一种在有序阵列中寻找某一特定元素的搜寻演算法。搜寻过程从阵列的中间元素开始,如果中间元素正好是要寻找的元素,则搜寻过程结束;如果某一特定元素大于或者小于中间元素,则在阵列大于或小于中间元素的那一半中寻找,而且跟开始一样从中间元素开始比较。如果在某一步骤阵列为空,则代表找不到。这种搜寻演算法每一次比较都使搜寻范围缩小一半。
二分搜寻在情况下的复杂度是对数时间,进行次比较操作(在此处是阵列的元素数量,是大O记号,是对数)。二分搜寻使用常数空间,无论对任何大小的输入资料,演算法使用的空间都是一样的。除非输入资料数量很少,否则二分搜寻比线性搜寻更快,但阵列必须事先被排序。尽管特定的、为了快速搜寻而设计的资料结构更有效(比如杂凑表),二分搜寻应用面更广。
举个例子,给定升序有序数列[0,1,2,4,5,6,7],搜寻2。
首先,检测最中间的元素4不是所搜寻的值,且4大于2。因为数列是升序有序的,所以如果2存在则肯定在4的左边。
然后,在4的左边半个数组中搜寻。先检测左半个数组的中间值1不是所搜寻的值,且1小于2。因为数组是升序有序的,所以若2存在则肯定在2与4之间的四分之一数组中。
再然后,在2和4之间的四分之一数组中搜寻。先检测中间值2是所搜寻的目标值。至此找到目标值。
将上述不断缩小搜寻范围的过程以二叉树的形式展示为:
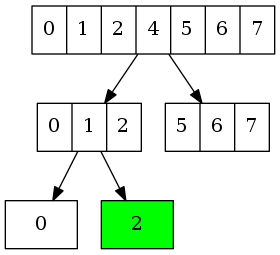
本题中的数组有些不同,是被旋转过的升序有序数组。搜寻方式依旧使用「二分搜寻法」,但判断目标值在左或右半部数组的方法有些许不同。
记旋转过的升序有序数组的第一个元素值为S,最后一个元素值为E,中间元素值为M。S, M, E之间的关系可分为三类:
- 数组没有旋转,
S和E之间都是升序有序的,。若目标值T小于M,则其一定位于M左侧S和M之间;若目标值T大于M,则其一定位于M右侧M和E之间。
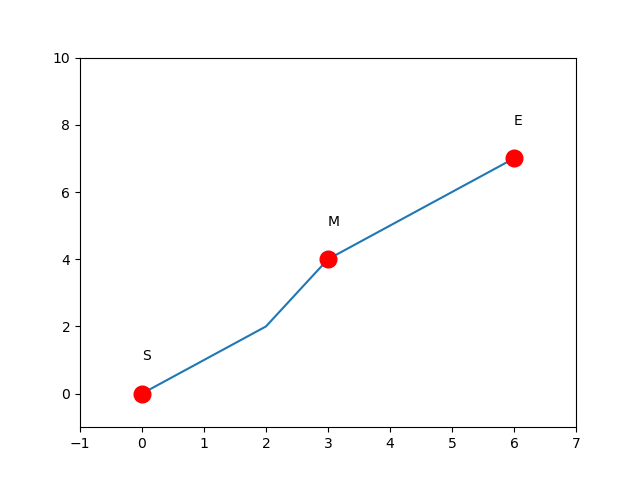
- 数组在
S和M之间旋转,。若目标值T小于M则其一定位于S和M之间;若目标值T大于S则其一定位于S和M之间;若目标值T大于M且小于S则其一定位于M和E之间。
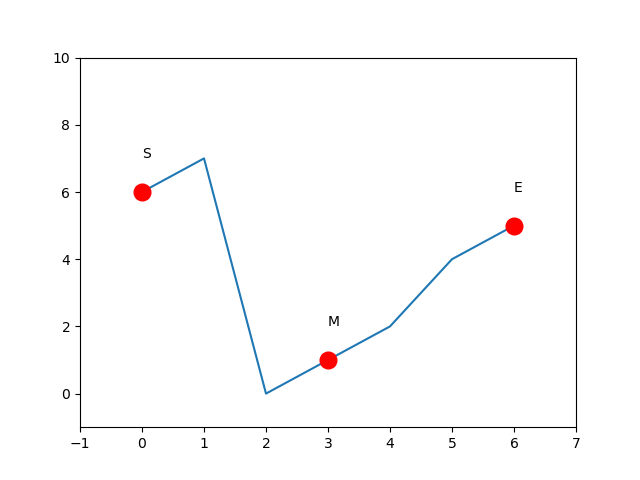
- 数组在
M和E之间旋转,。若目标值T大于S且小于M则其一定位于S和M之间;若目标值T小于M且小于S则其一定位于M和E之间;若目标值T大于M则其一定位于M和E之间。
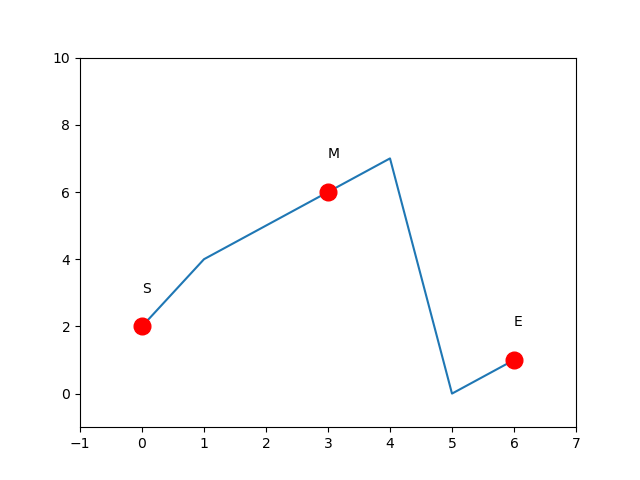
代码
首先,检测头尾是否为目标值。
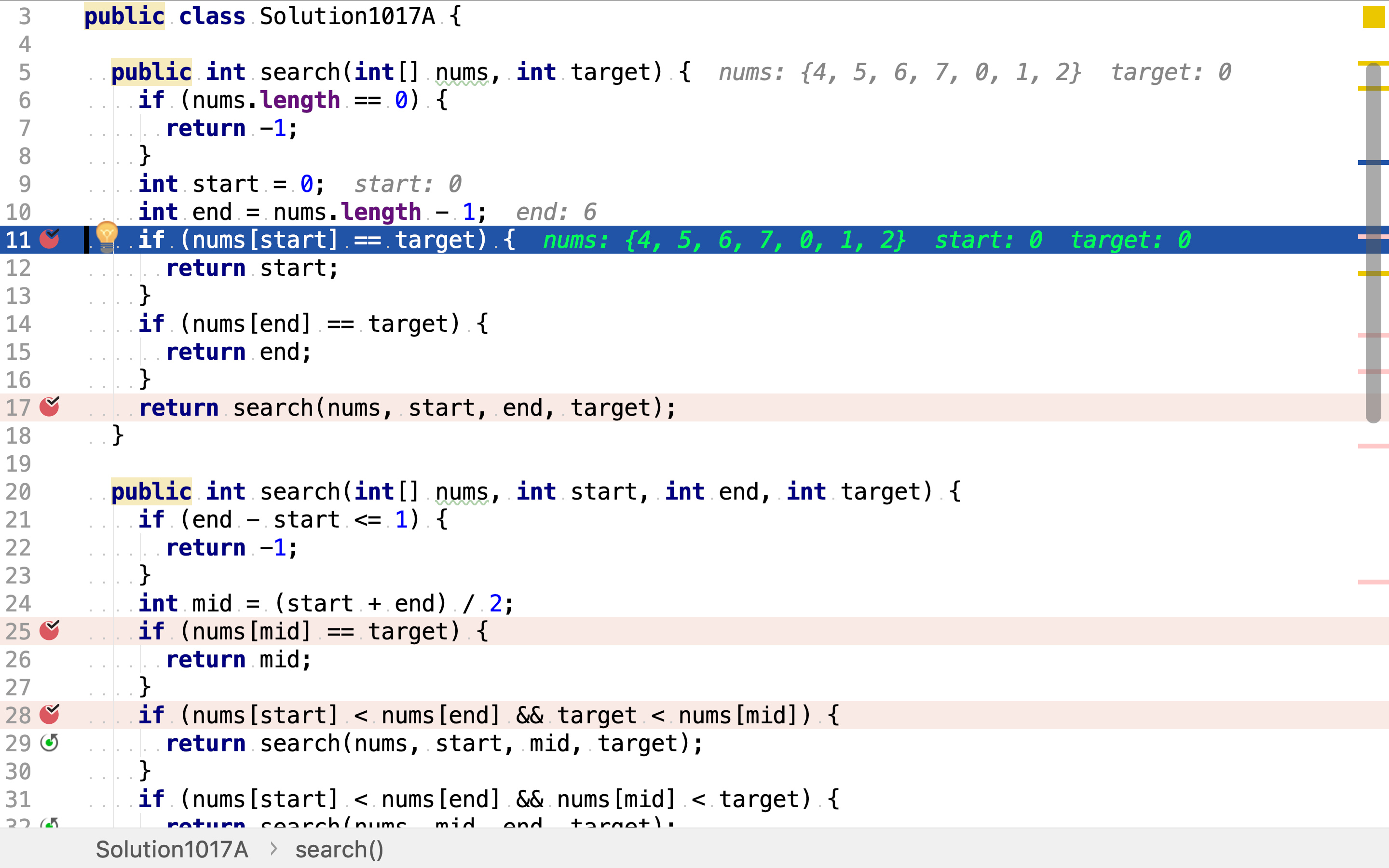
然后,开始二分搜寻。
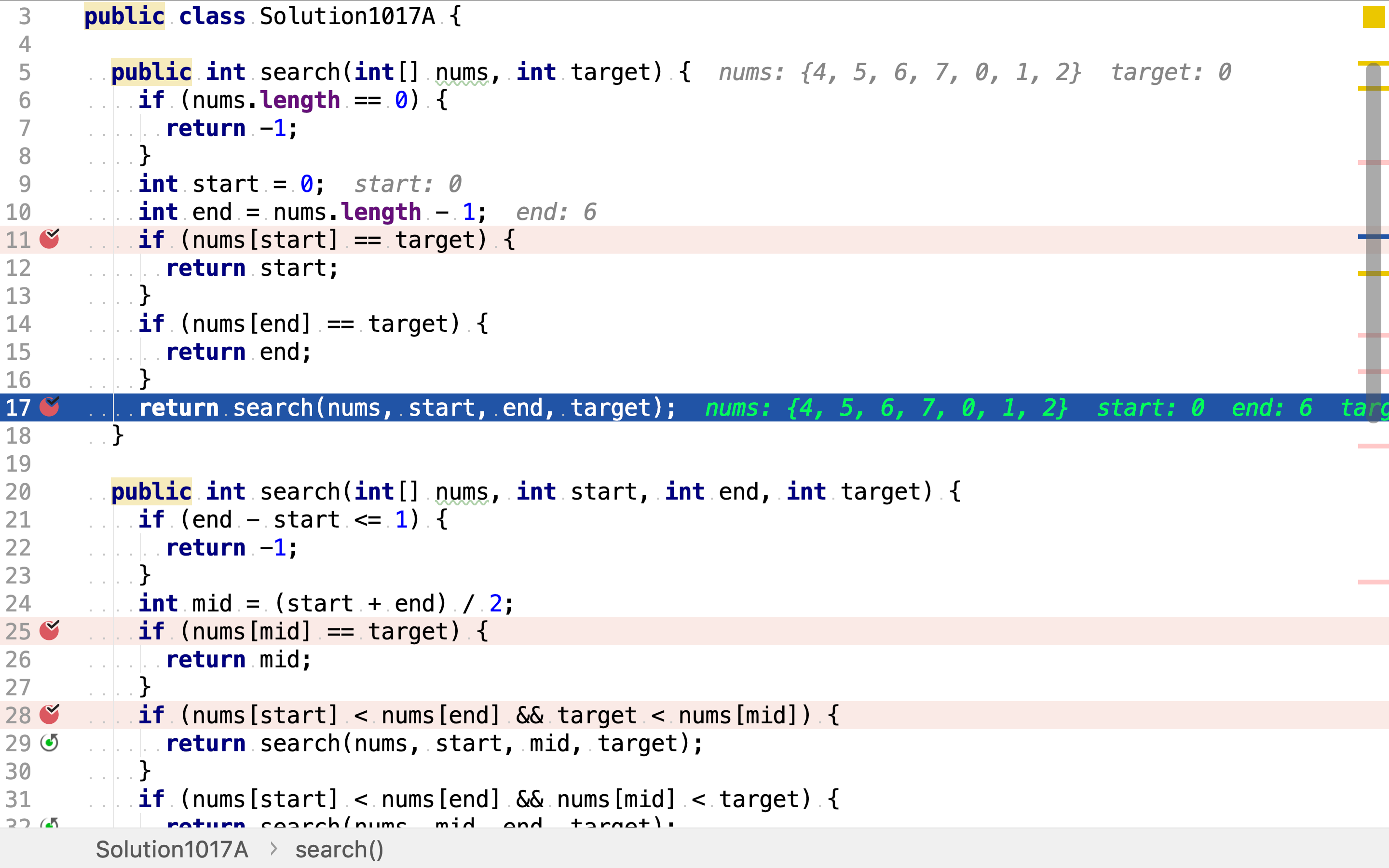
二分搜寻先计算中间位置并检测目标值是否位于中间位置。
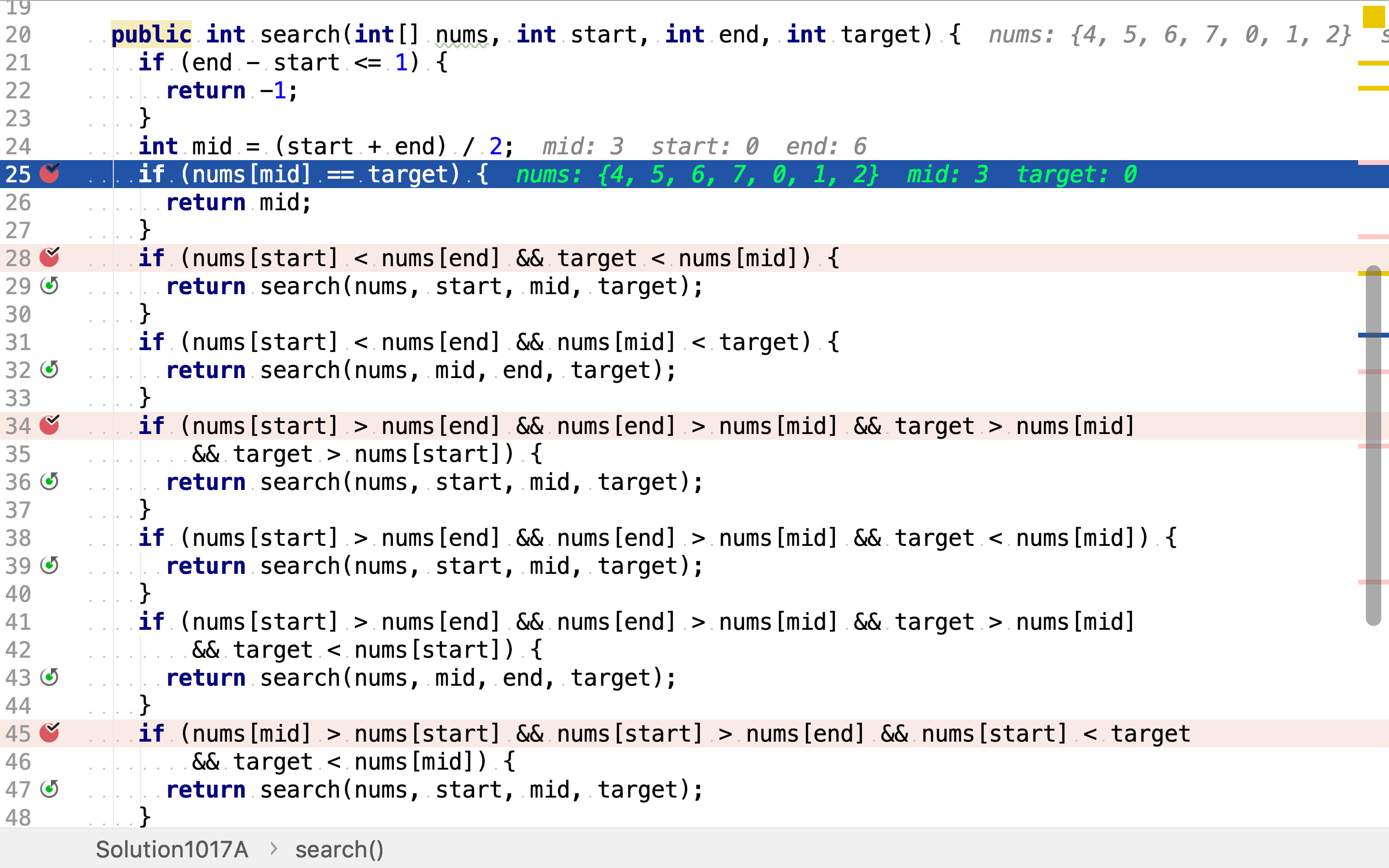
若目标值不位于中间位置,则判断其位于中间位置左侧或右侧。这𥚃分三种情况。
第一种,数组没有旋转。若目标值小于中间值则其位于左侧,若目标值大于中间值则其位于右侧。
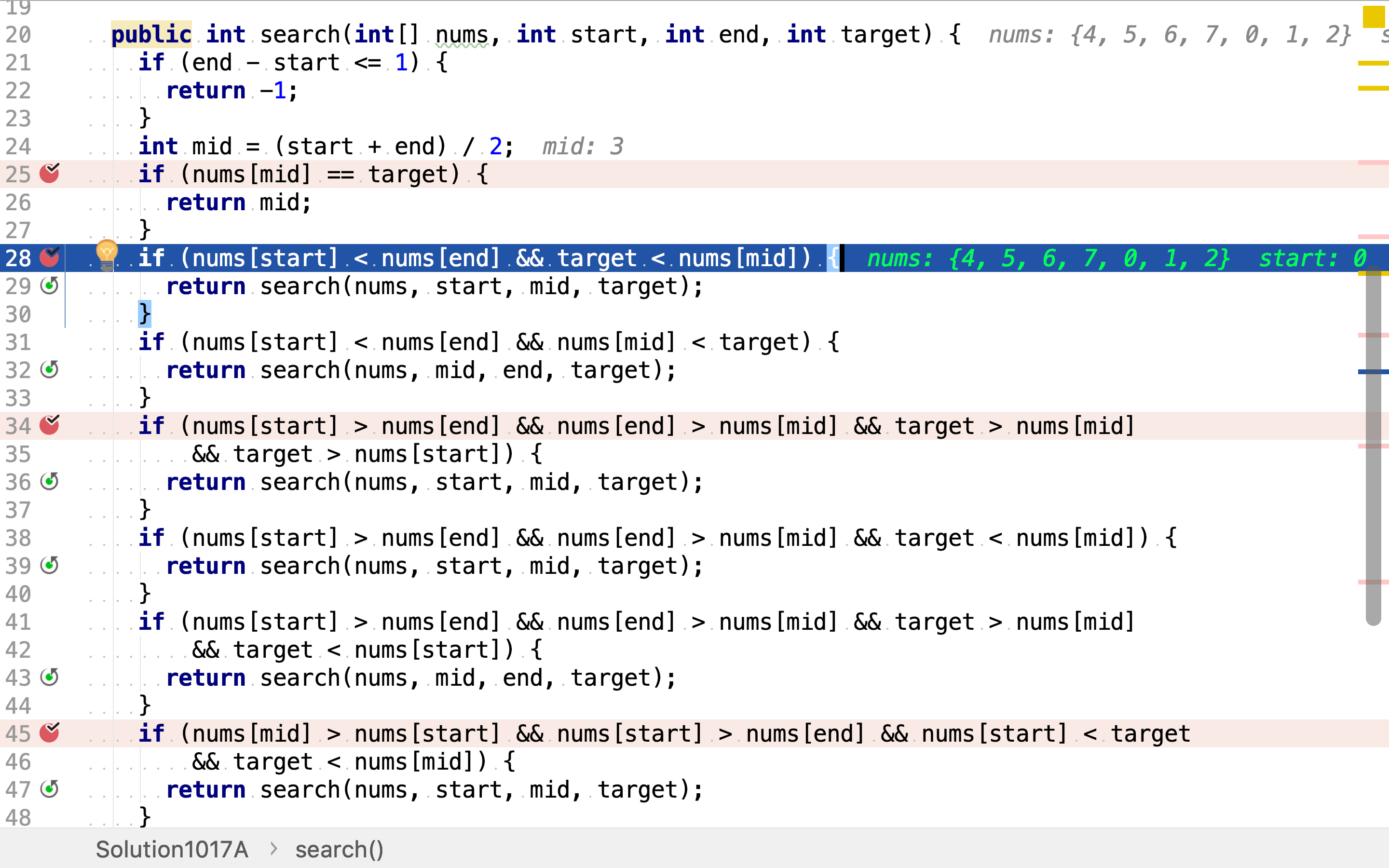
第二种,数组在S和M之间旋转了。若目标值大于中间值且大于头部值,则其位于左侧;若目标值小于中间值,则其位于左侧;若目标值大于中间值且小于头部值,则其位于右侧。
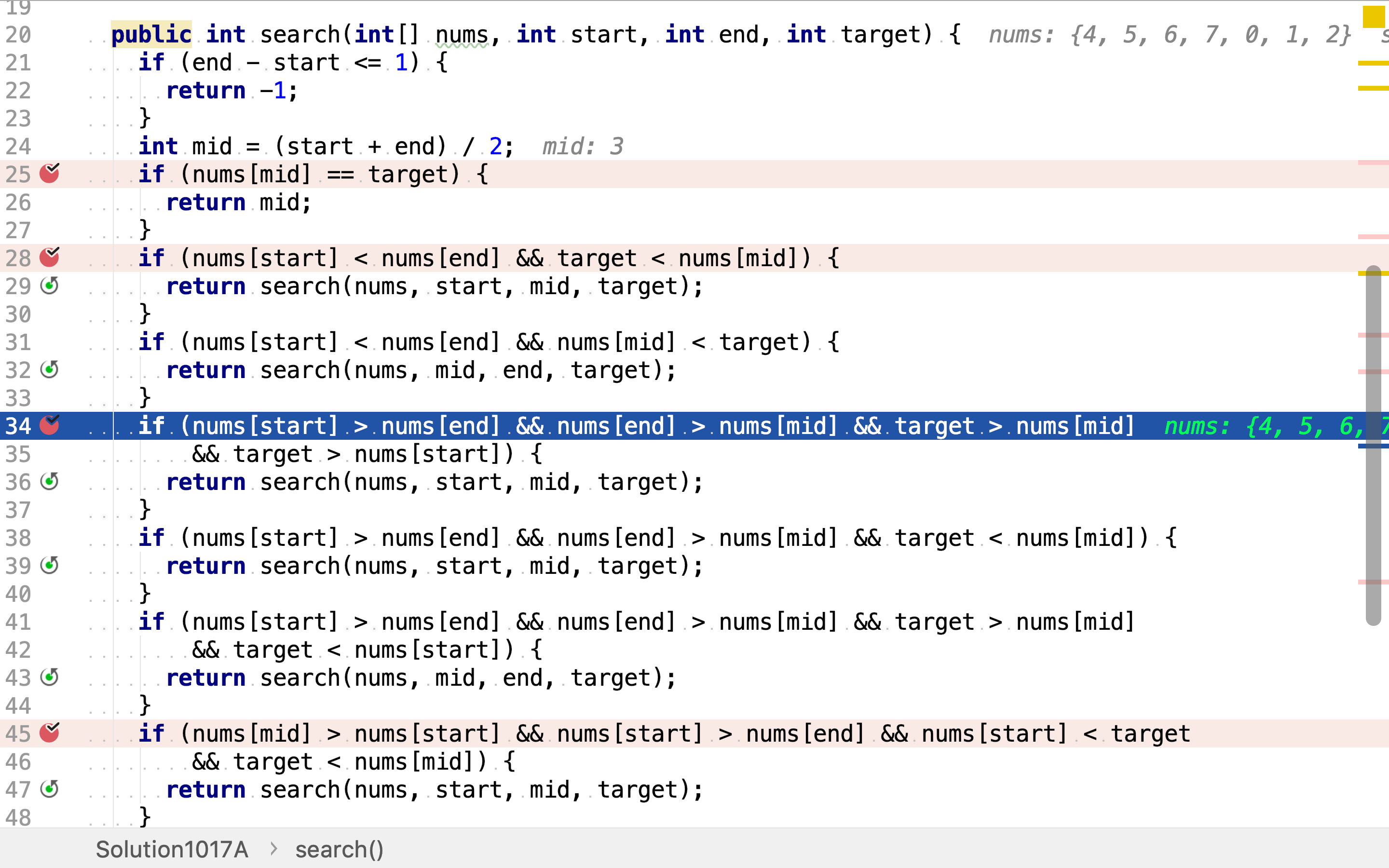
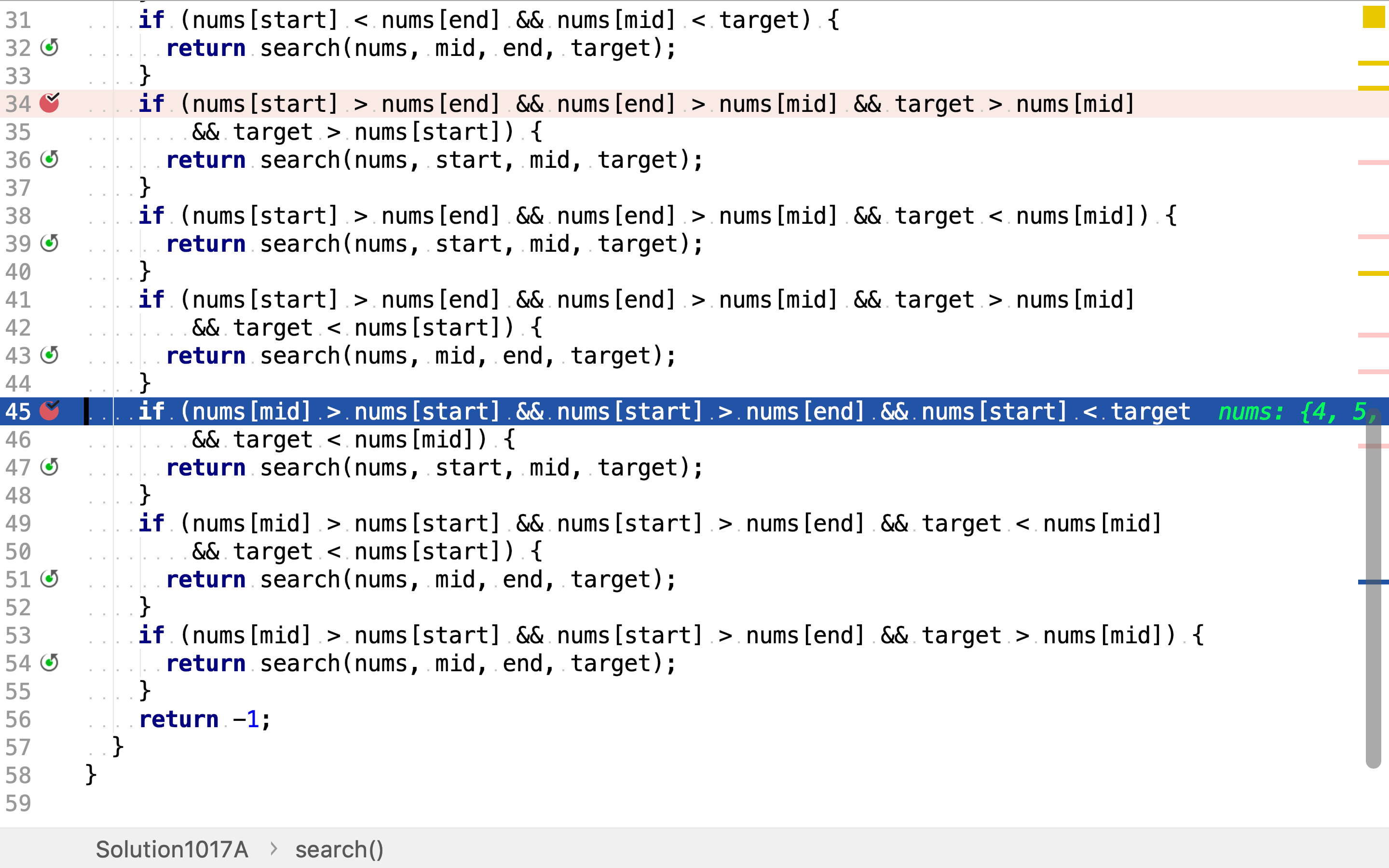
第三种,数组在M和E之间旋转了。若目标值大于头部值且小于中间值,则其位于大侧;若目标值小于中间值且小于头部值,则其位于右侧;若目标值大于中间值,则其位于右侧。
复杂度分析
时间复杂度
最坏情况下,将数组二分至仅有一个元素。将一个长的数组二分至仅有一个元素,而要次。所以时间复杂度为。
空间复杂度
使用了三个局部变量start, end, mid。空间复杂度为。