最大子序和
题目
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4], 输出: 6 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。进阶:
如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的分治法求解。
穷举法
连续子数组由起止点确定。起始点从第一个到最后都可,终止点从起始点(只包含一个元素)到最后一个皆可。
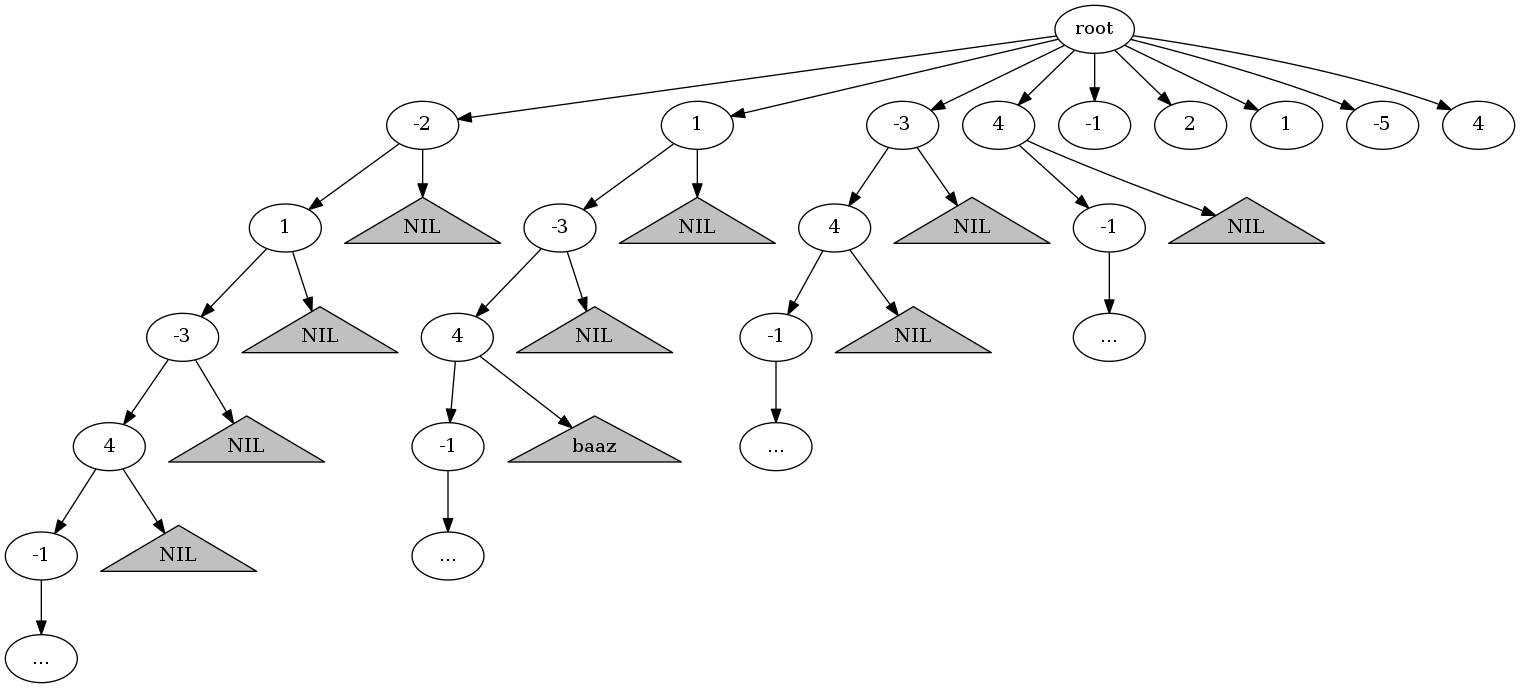
将所有子数组组合以树的形式展现。从根到叶子节点的路径所包含的节点就是一个子数组。比如,root -> -2 -> NIL表示子数组[-2]; root -> -2 -> 1 -> NIL表示子数组[-2, 1]。
代码
package io.github.rscai.leetcode.bytedance.dynamic;
public class Solution1029A {
public int maxSubArray(int[] nums) {
int max = Integer.MIN_VALUE;
for (int start = 0; start < nums.length; start++) {
int accum = nums[start];
if (accum > max) {
max = accum;
}
for (int end = start + 1; end < nums.length; end++) {
accum += nums[end];
if (accum > max) {
max = accum;
}
}
}
return max;
}
}
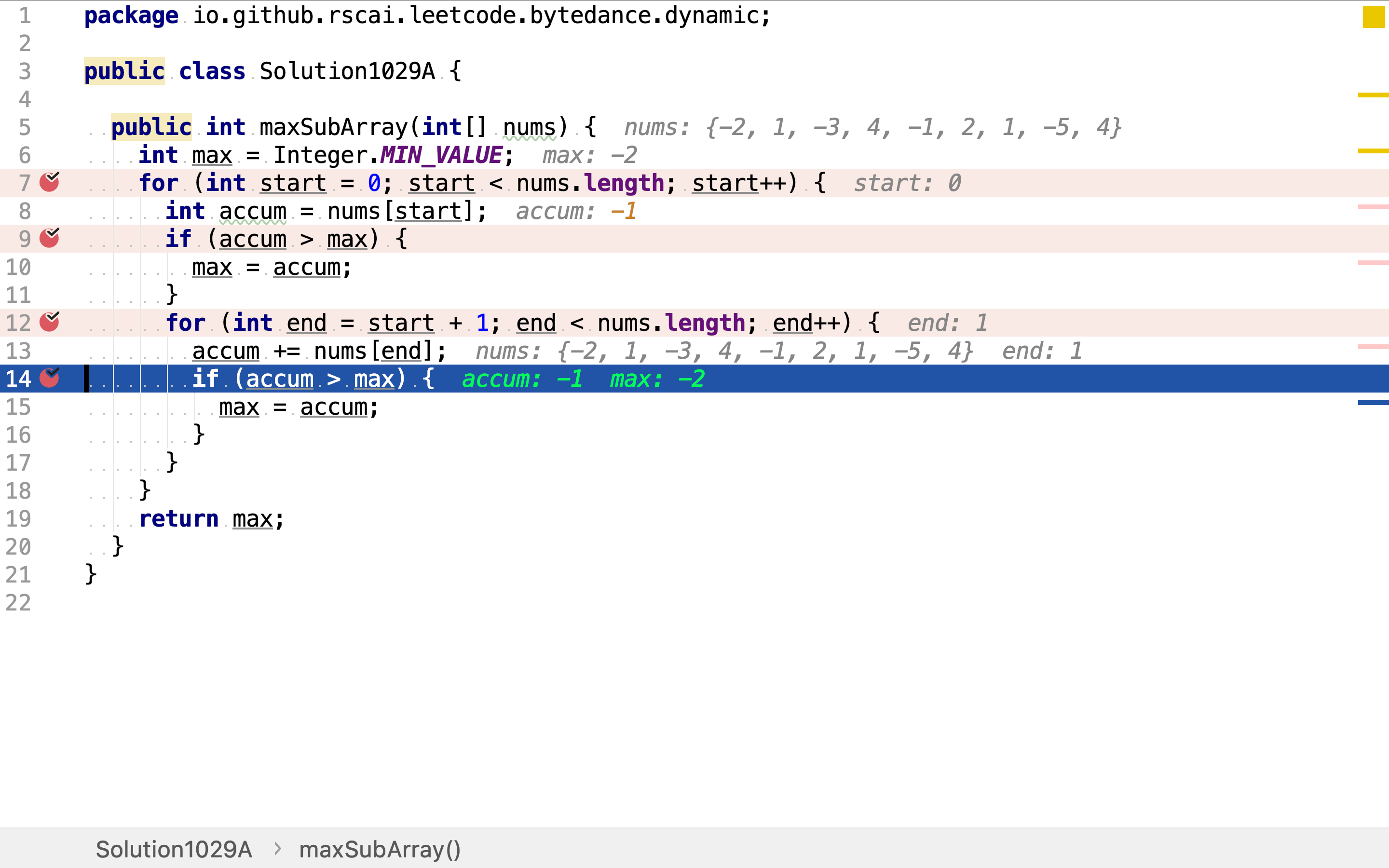
首先,选择起始点。任一位置都可以是起始点。
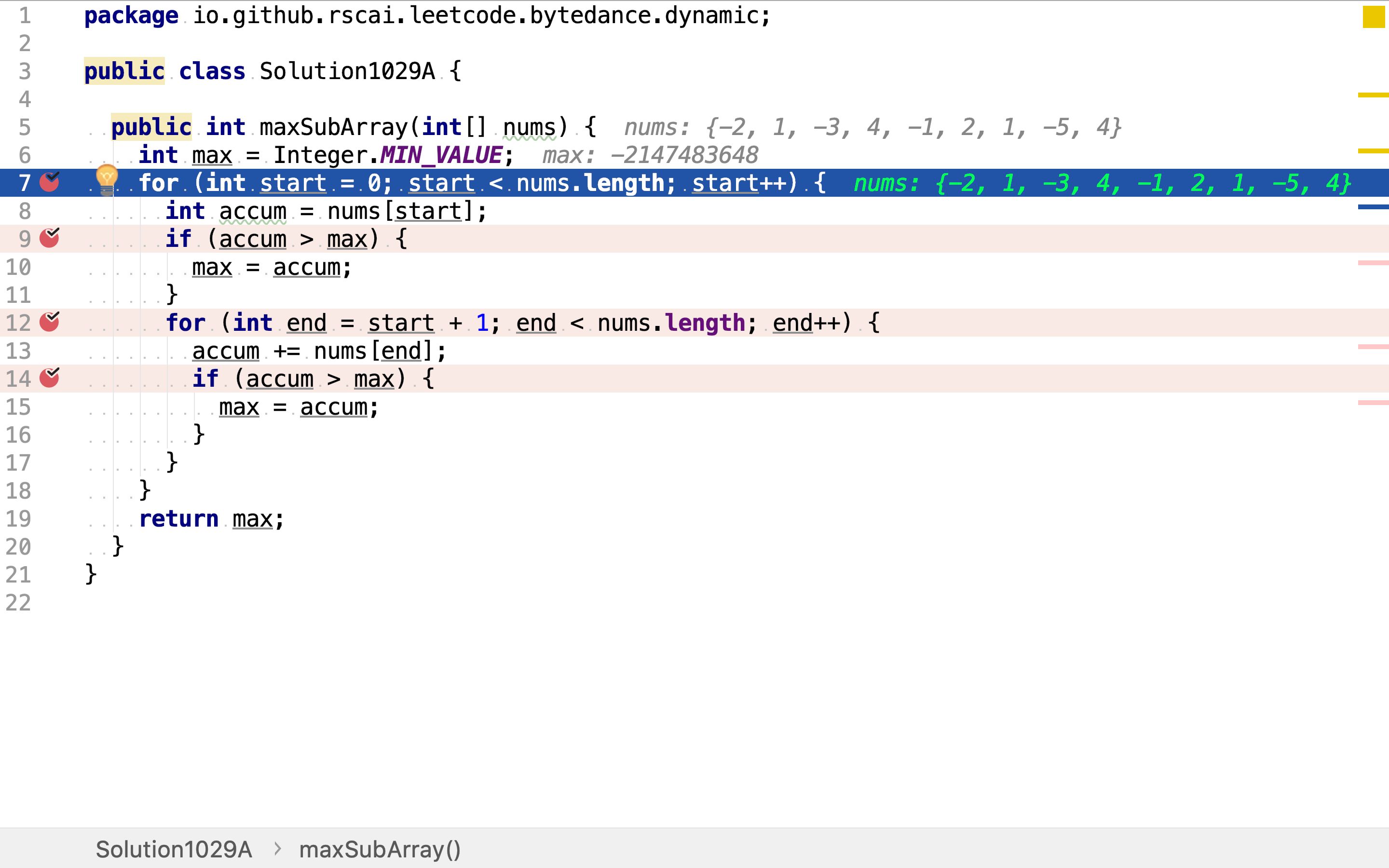
然后,比较单一元素值与当前最大值,以覆盖仅包含一个元素的子数组。
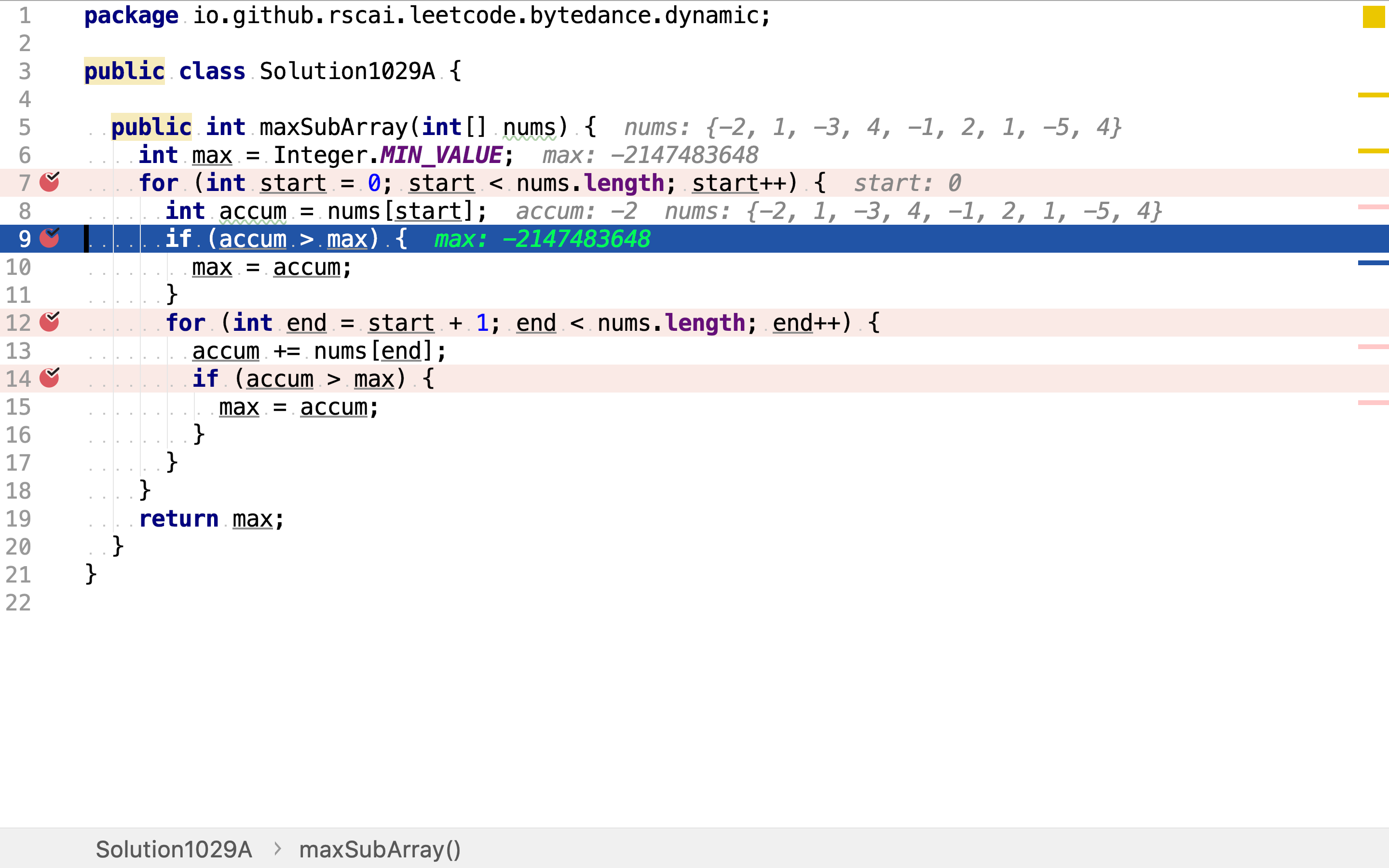
再然后,选择终止点。起始点往后任一位置都可以是终止点。
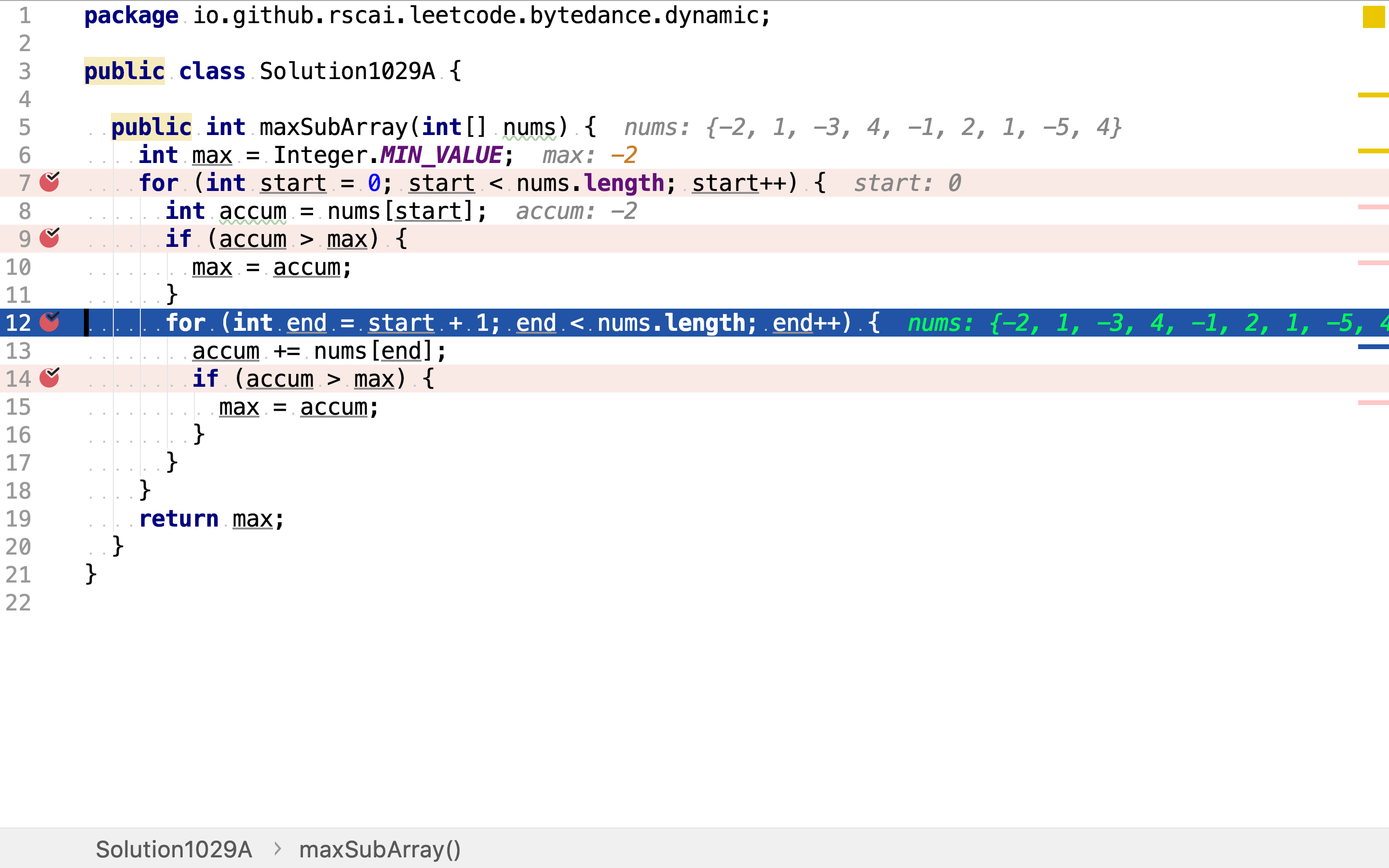
最后,累加起止点之间的元素值,并与当前最大值比较。
复杂度分析
时间复杂度
其共有两层循环,内层循环次数与外层取值有关。假设外层取值为,则内层循环次数为。时间复杂度为:
空间复杂度
使用两个变量max和accum。空间复杂度为:
动态规划法
将子数组组合以树的形式展现,可以发现有很多子树是重复的。第一层(根节点为第0层)节点的左子树完全等于以右侧兄弟节点为根的子树。
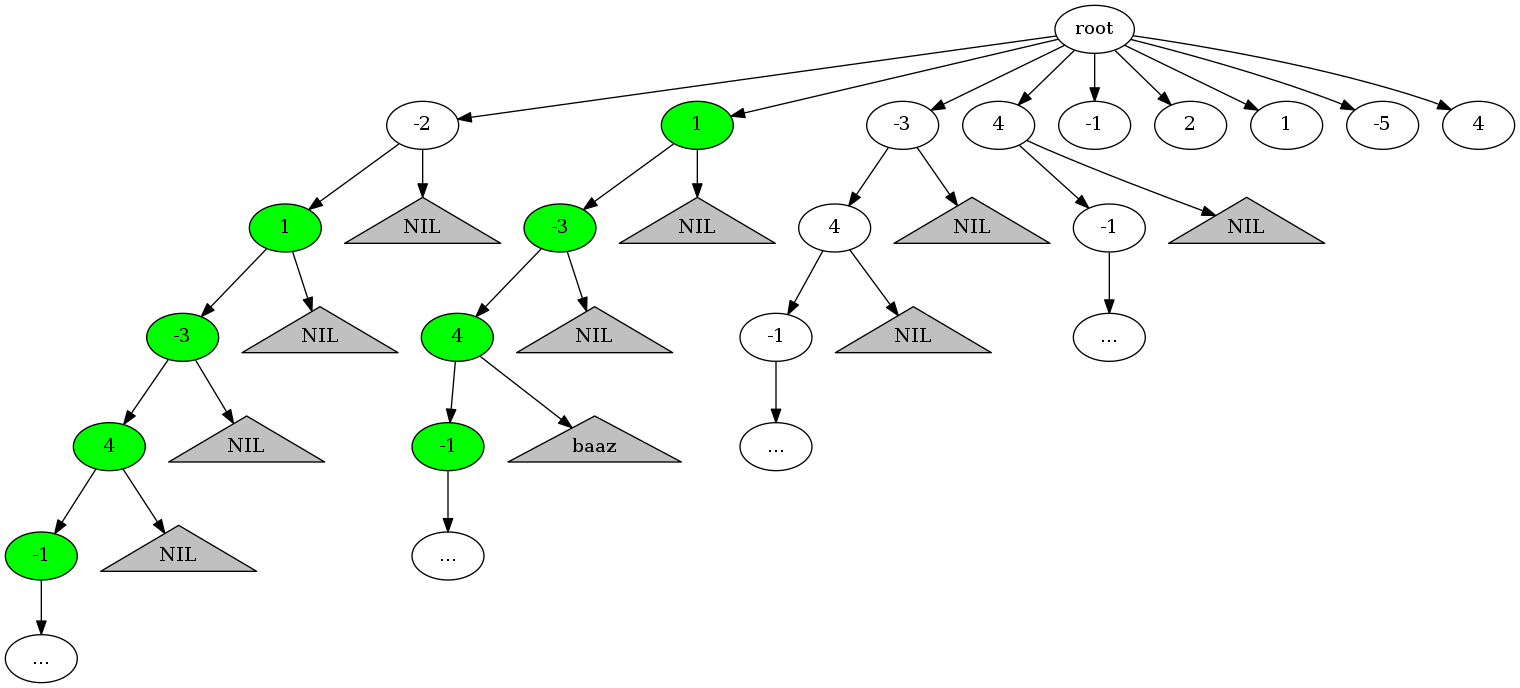
而且,连续子数组的和有一个特性。假设一个连续子数组有a和b两个子数组组成。如果a的和小于零,则a和b组成的子数组和肯定小于b的和。再结合子树重复性,可以得出以下论断:
- 如果某个节点到根节点路径上所有节点值的和小于或等于0,则无需探索其子树。因为,从根节点到其任意叶子节点路径上值的和绝不会大于从其子节点到叶子节点路径上值的和。且其右侧兄弟子树覆盖了其子树。
代码
package io.github.rscai.leetcode.bytedance.dynamic;
public class Solution1029B {
public int maxSubArray(int[] nums) {
int max = Integer.MIN_VALUE;
int accum = 0;
for (int index = 0; index < nums.length; index++) {
accum += nums[index];
if (accum > max) {
max = accum;
}
if (accum < 0) {
accum = 0;
}
}
return max;
}
}
一次遍历整个数组。
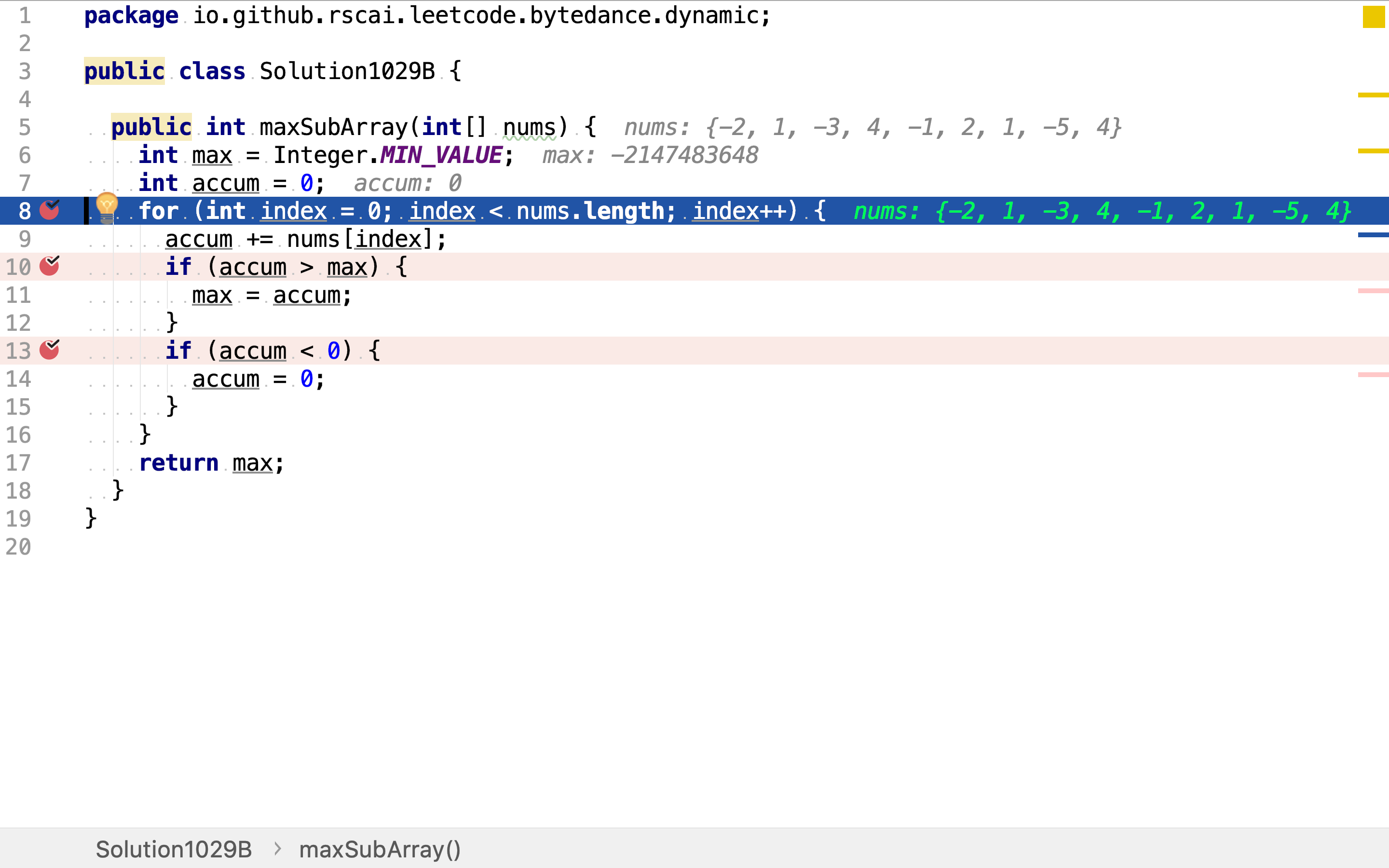
比较从根节点至今的累加值和当前最大值。如果大于当前最大值,则表明找到了一个和更大的连续子数组。
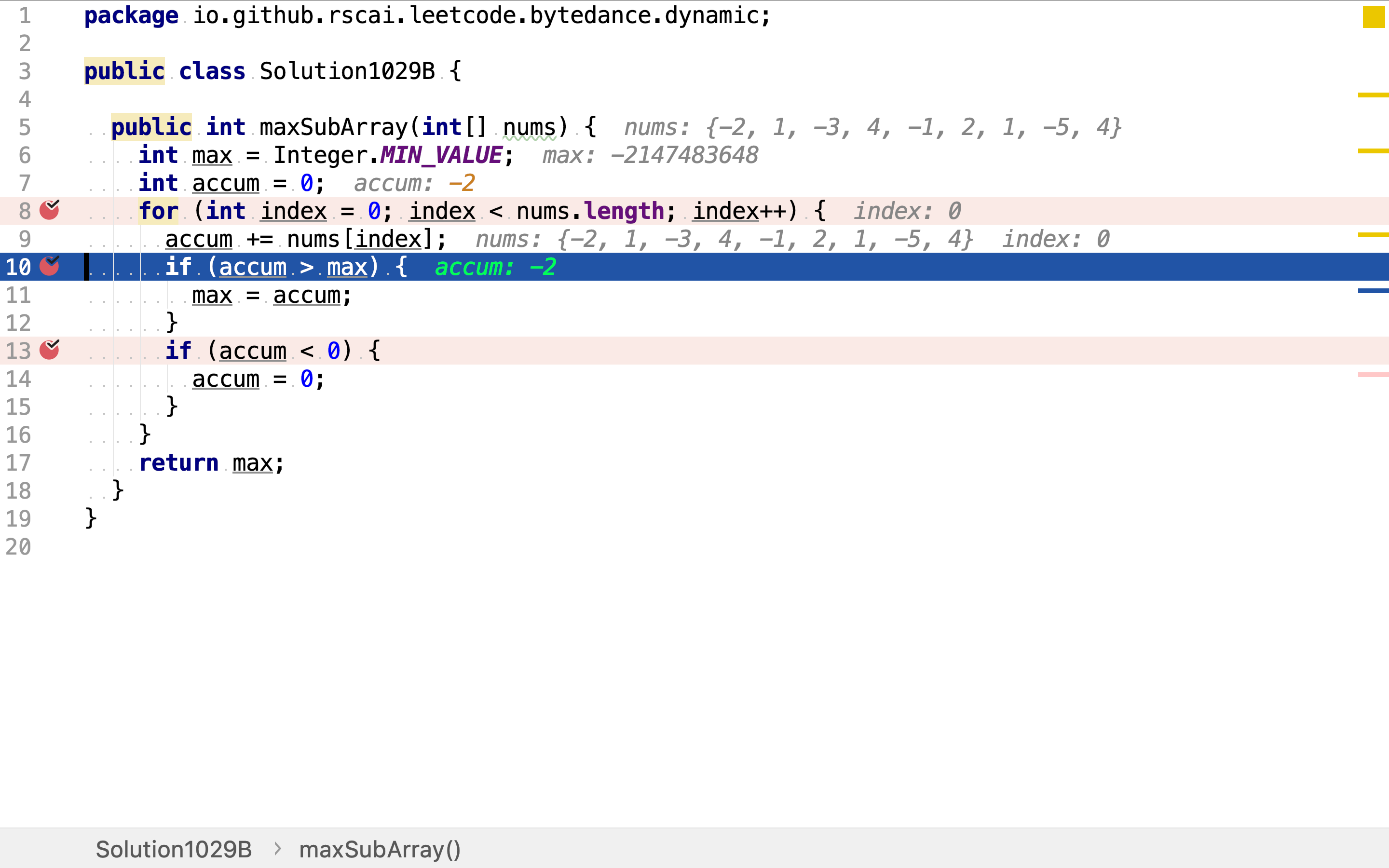
如果从根节点到今的累加值小于0,则表明无需再探索其子树了。直接清零累加值,等同于从下一个位置(在树结构中,则是右侧兄弟节点)再开始累加。
复杂度分析
时间复杂度
只遍历了数组一次,所以时间复杂为:
空间复杂度
使用了两个变量max和accum。空间复杂度为: