三⻆形最小路径和
题目
给定一个三角形,找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。
例如,给定三角形:
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
说明:
如果你可以只使用 O(n) 的额外空间(n 为三角形的总行数)来解决这个问题,那么你的算法会很加分。
穷举法
罗列所有路径并求其和,再选取最小值。第一步只有一个选择,从第二步开始每一步都有两个选择。
举个例子,给定三角形:
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
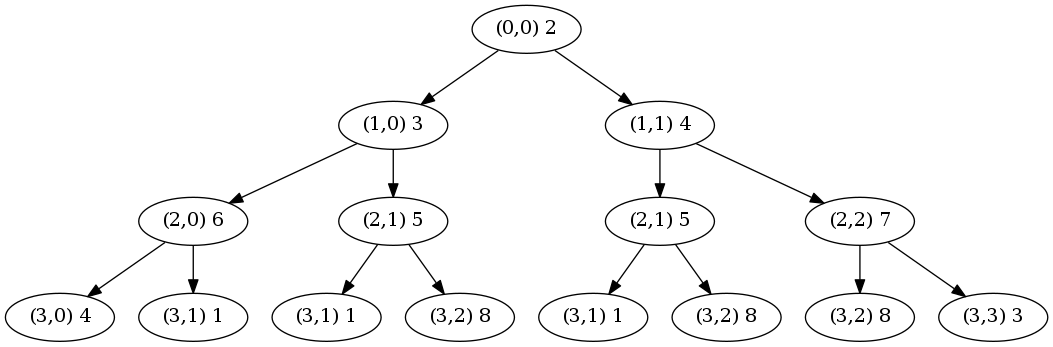
将所有路径以树的形式展现。
第一步只有一个选择,2。
第二步有两种选择,左下方3和右方下4。
第三步受限于第二步的选择,如果第二步选了3则第三步可选择6或5,如果第二步选了4则第三步可选择5或7`。
依此类推。。。
也就是说,每一步都会分裂出两种选择。若三⻆形的高度为d,则路径总数为。
用形式化语言描述:
- 若第i行选择了第k个元素,则第i+1行可选择第k和第k+1个元素
- 第一行只能选择第0个元素
代码
package io.github.rscai.leetcode.bytedance.dynamic;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.List;
public class Solution1030A {
public int minimumTotal(List<List<Integer>> triangle) {
List<Integer> pathLengths = pathLengths(0, triangle);
int min = Integer.MAX_VALUE;
for (Integer pathLength : pathLengths) {
if (pathLength < min) {
min = pathLength;
}
}
return min;
}
private List<Integer> pathLengths(int startIndex, List<List<Integer>> rows) {
if (rows.size() == 0) {
return Collections.singletonList(0);
}
List<Integer> firstRow = rows.get(0);
List<List<Integer>> remainRows = rows.subList(1, rows.size());
List<Integer> allPathLengths = new ArrayList<>();
List<Integer> firstElementIndexes = Arrays.asList(startIndex);
if (firstRow.size() > startIndex + 1) {
firstElementIndexes = Arrays.asList(startIndex, startIndex + 1);
}
for (Integer firstElementIndex : firstElementIndexes) {
for (Integer remainPathLength : pathLengths(firstElementIndex, remainRows)) {
allPathLengths.add(firstRow.get(firstElementIndex) + remainPathLength);
}
}
return allPathLengths;
}
}
整个问题可以认为是以某个点为三⻆形的顶点,罗列出所有可能的路径的和。这𥚃使用递归实现。
首先,定义一个函数pathLengths。给定顶点位置startIndex和下方其余行rows,该函数返回所有可行的路径的和。
pathLengths将问题拆分为两部份:从其余行中的第一行中取相邻的点;以第一行中所取的点为三⻆形的顶点,求在剩余行中所有路径的和。
先把行分为第一行firstRow
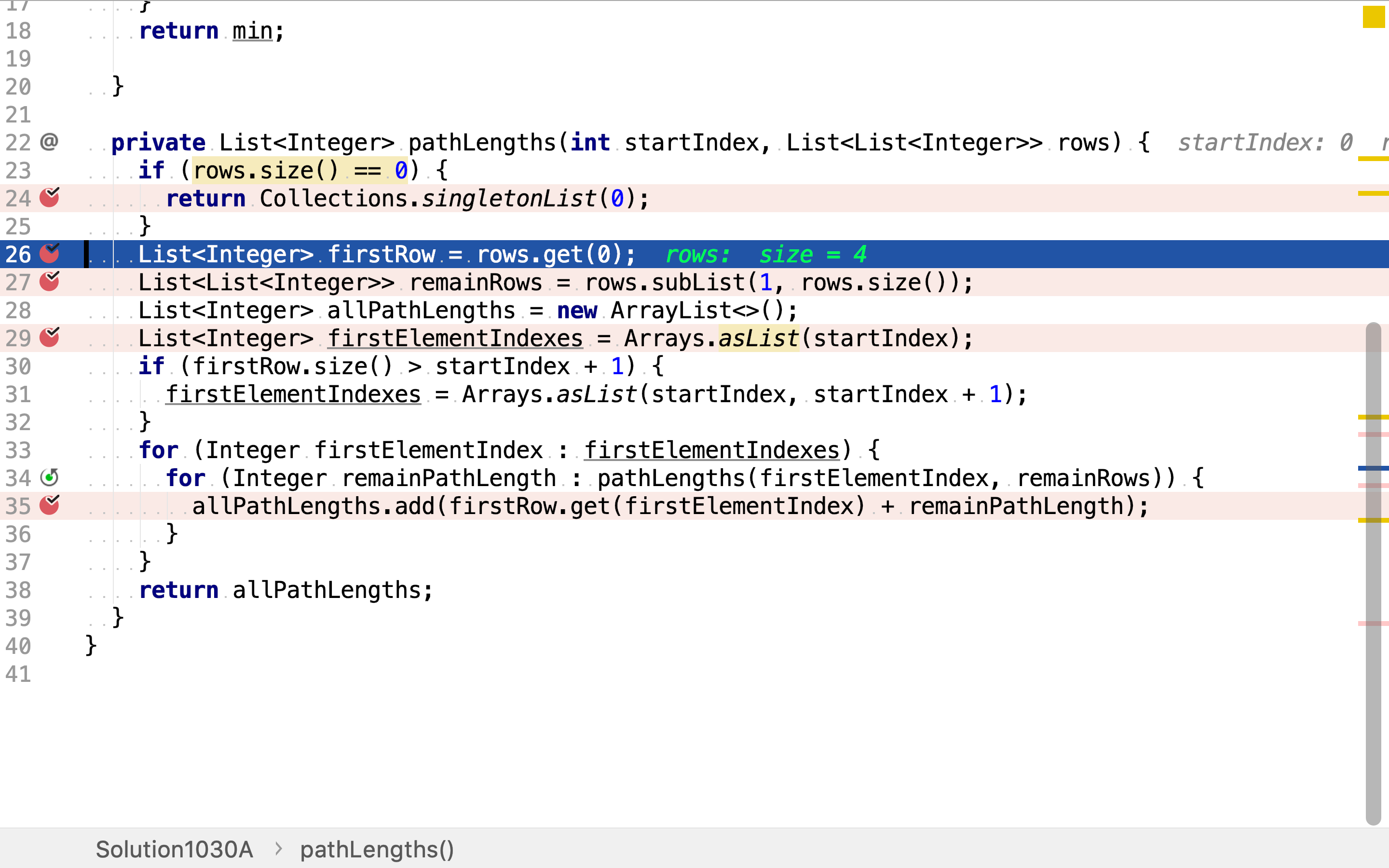
和其余行remainRows
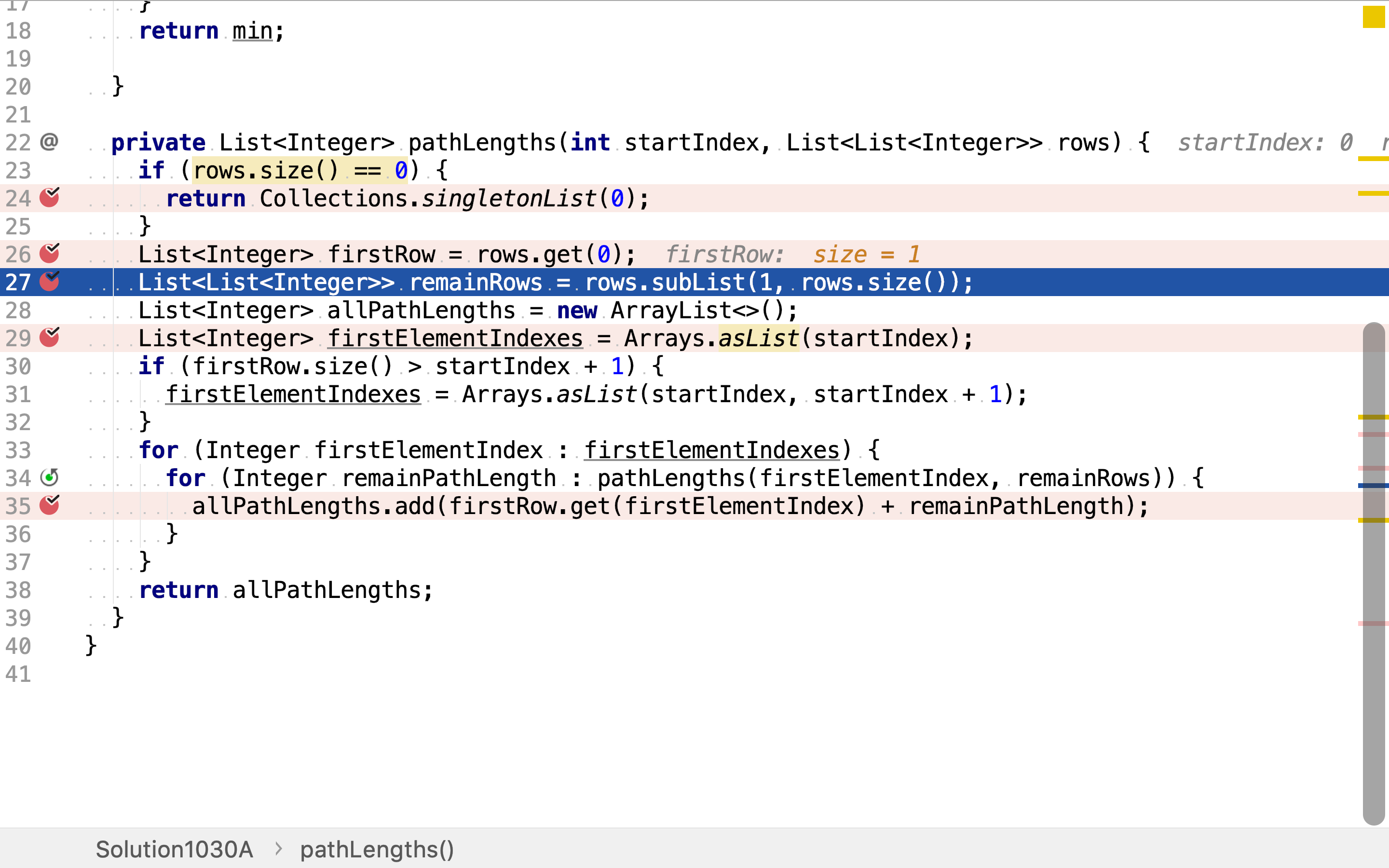
然后,解决「足够简单的问题」:在第一行𥚃取相邻点。下标相同和下标多1的点与上一行的点是相邻的。
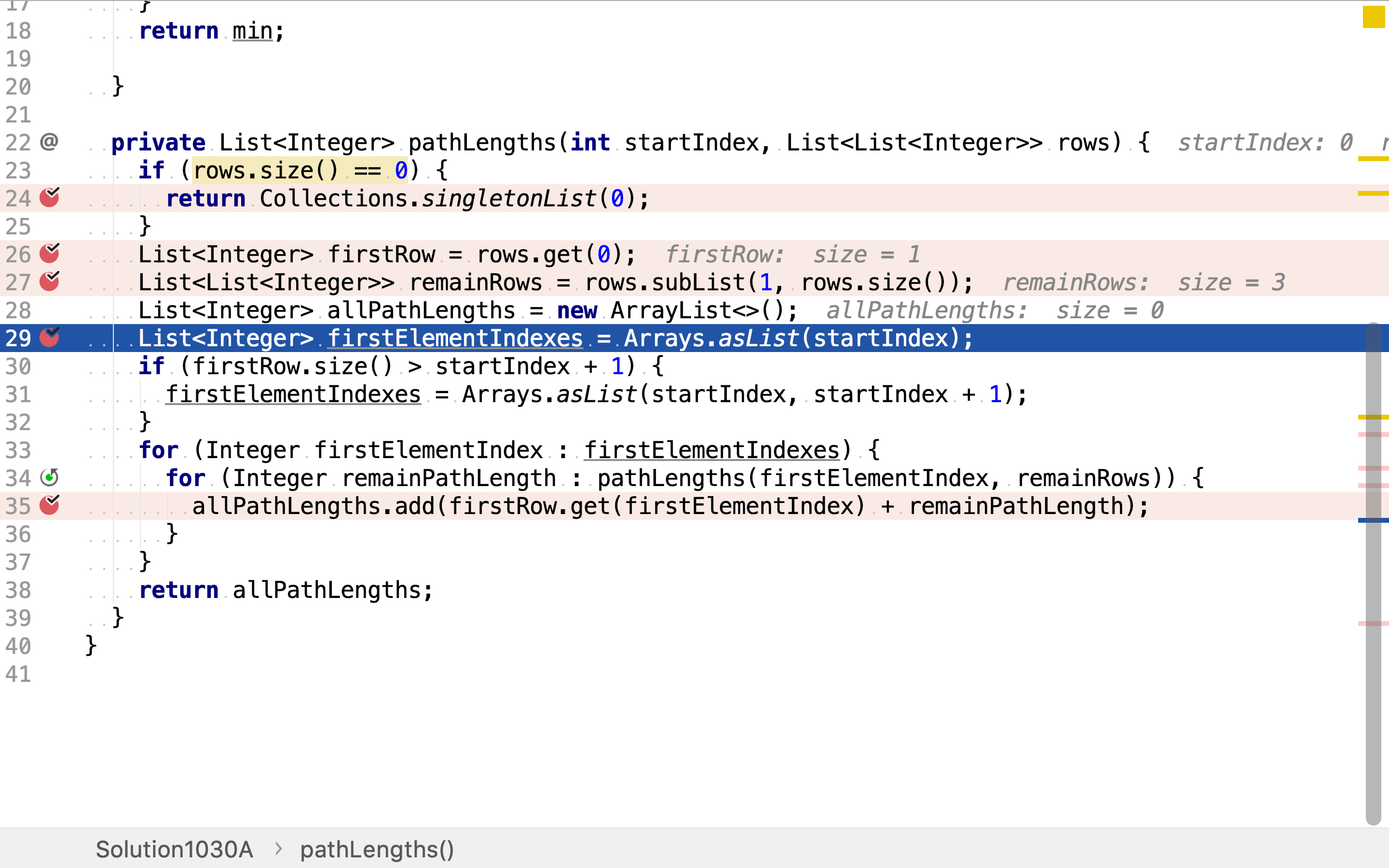
再然后,用递归调用的方式解决「其余的问题」:以第一行中的点为三⻆形顶点,求在其余行中所有路径的和。
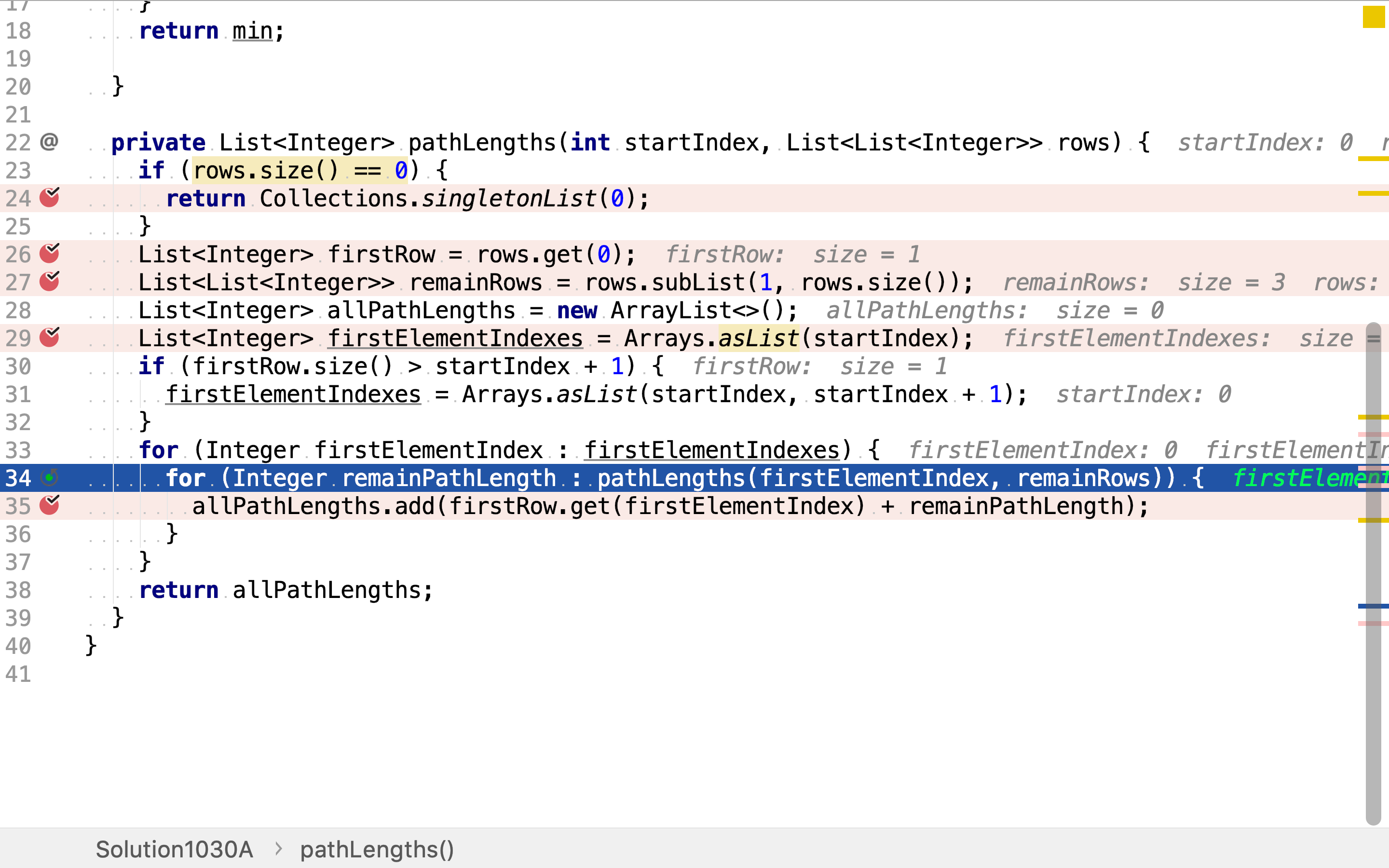
再然后,将「简单问题」的解和「其余问题」的解归併。第一行中与上方相邻的点有一至两个,其余行中的路径也有多个。所以将两个解集归併产生了更多的解。
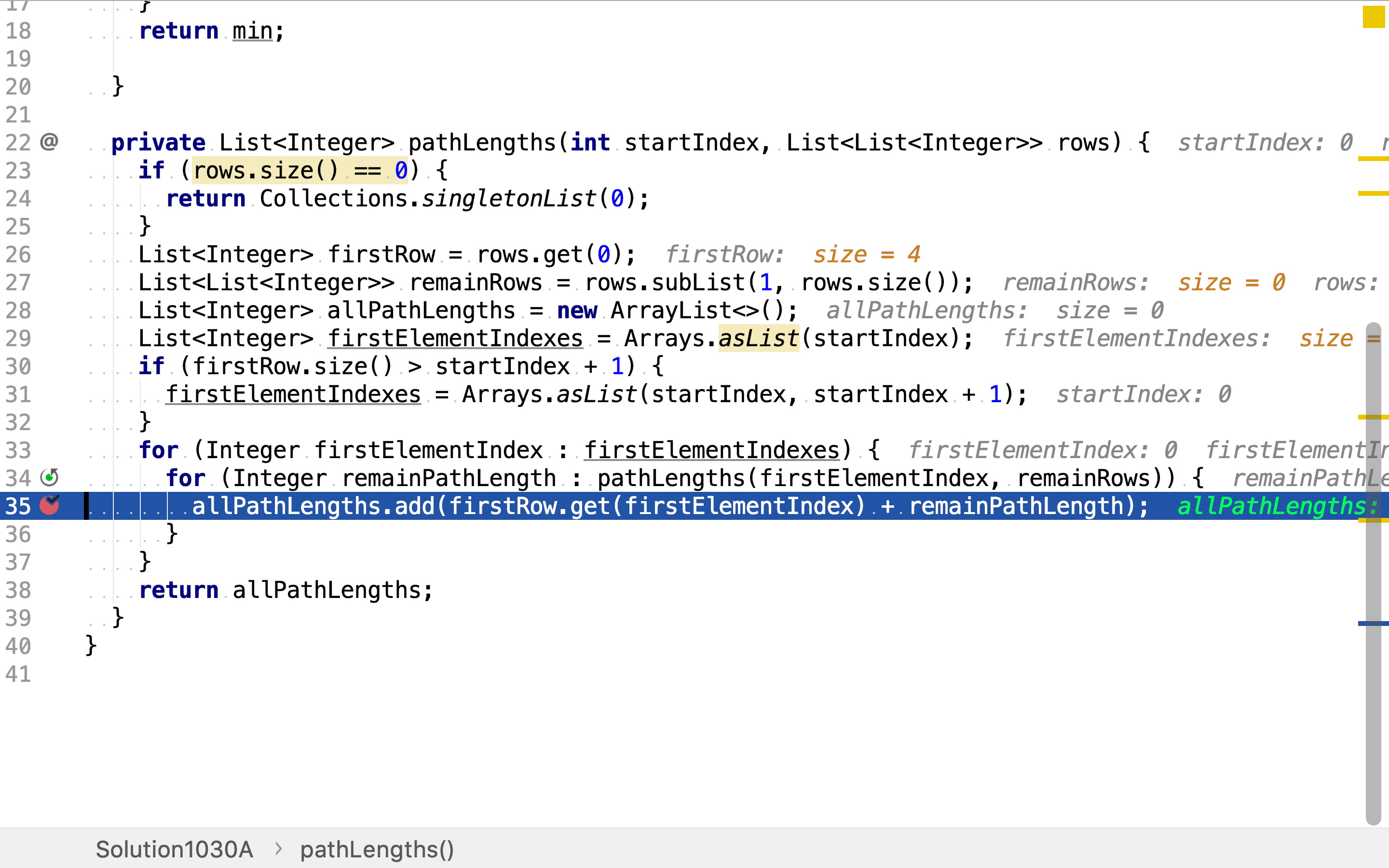
递归的终止条件是没有「其余行」。
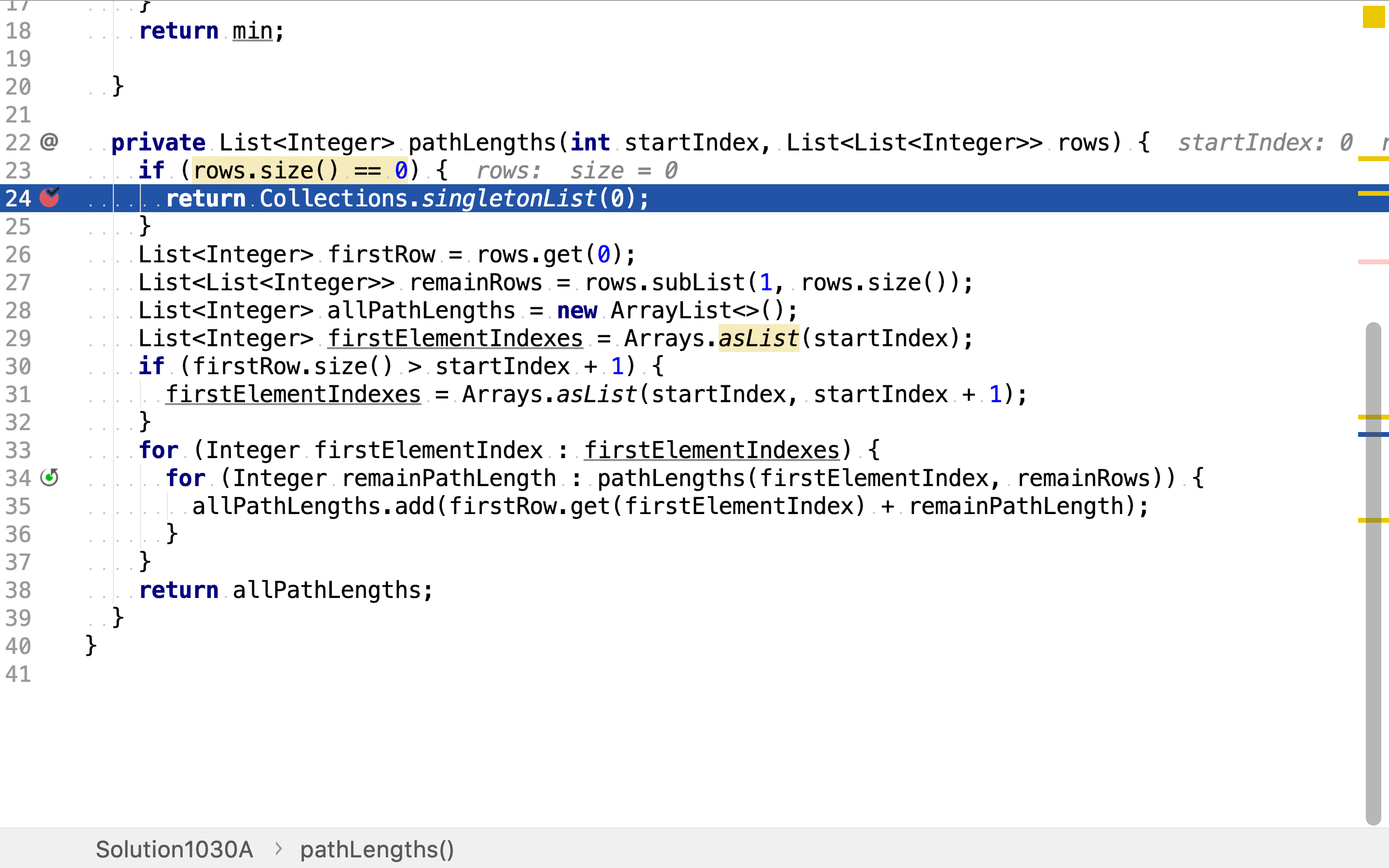
最后,一次遍历所有路径和,求出最小值。
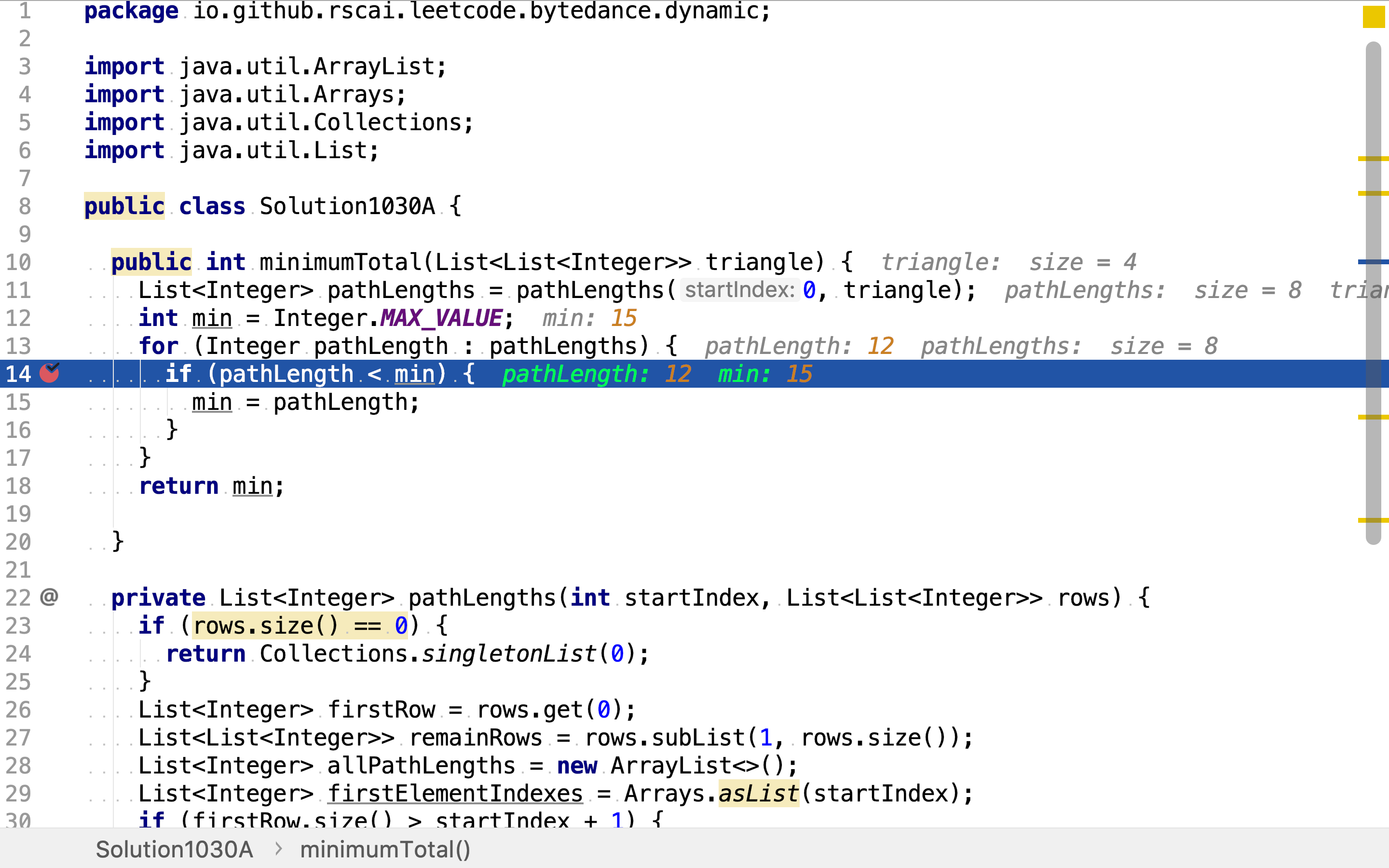
复杂度分析
时间复杂度
pathLengths的调用深度与第一行firstRow在总体中所处的高度相关。第一层pathLengths调用中,firstRow是第一行,第二层pathLengths调用中,firstRow是第二行。依山一心类推。且每一次pathLengths会调用两次自身(任一点在下一行中有两个相邻点)。所以,pathLengths的调用次数为,为三⻆形的高度。
以为三⻆形中点的总数,则:
所以,时间复杂度为:
空间复杂度
pathLengths的最大调用深度是。所以,空间复杂度是:
动态规划法
将穷举的过程用树表示。可以发现很多重复的子树。
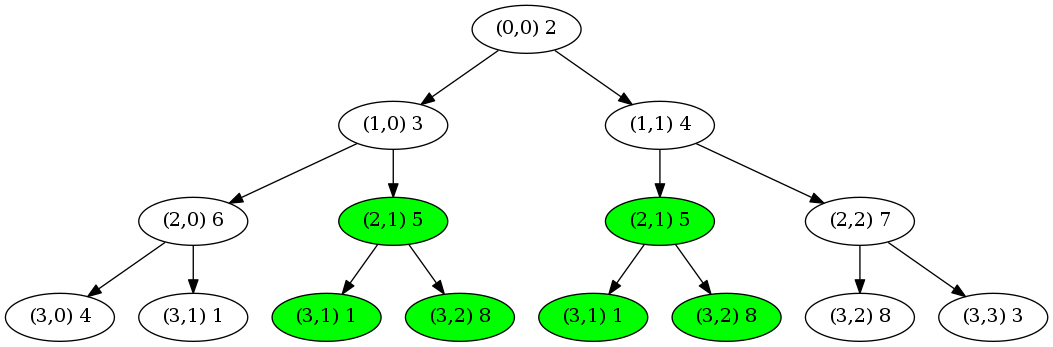
动态规划法就是暂存这此子树的解,供后续使用,从而减少计算量。
递推公式为:
其中,为以第r行第c列元素为起点的最短路径和,为第r行第c列元素的值,为总行数。
代码
package io.github.rscai.leetcode.bytedance.dynamic;
import java.util.Arrays;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
import java.util.function.BiFunction;
public class Solution1030B {
public int minimumTotal(List<List<Integer>> triangle) {
BiFunction<Integer, Integer, Integer> minPathLength = new BiFunction<Integer, Integer, Integer>() {
private Map<String, Integer> cache = new HashMap<>();
@Override
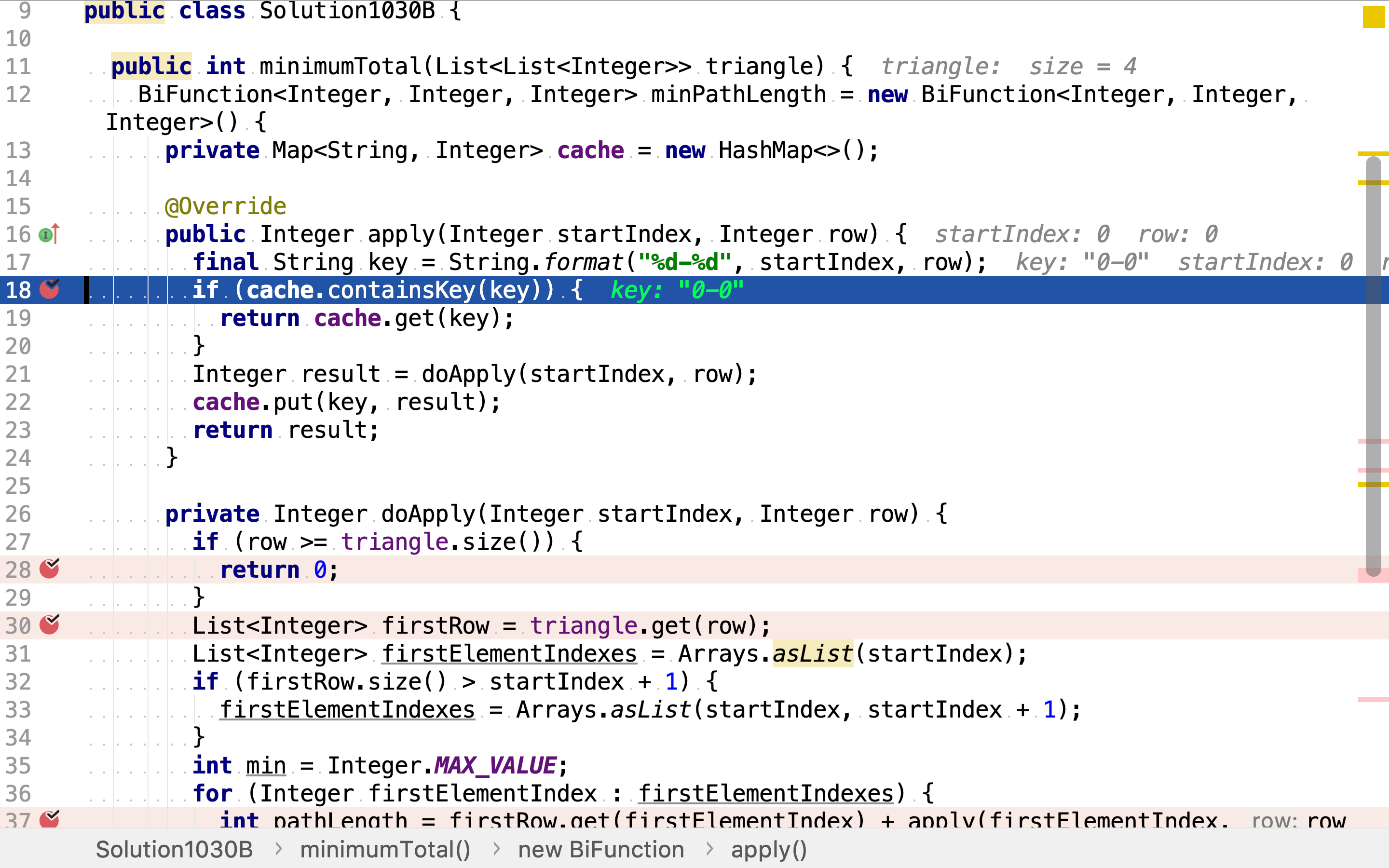
public Integer apply(Integer startIndex, Integer row) {
final String key = String.format("%d-%d", startIndex, row);
if (cache.containsKey(key)) {
return cache.get(key);
}
Integer result = doApply(startIndex, row);
cache.put(key, result);
return result;
}
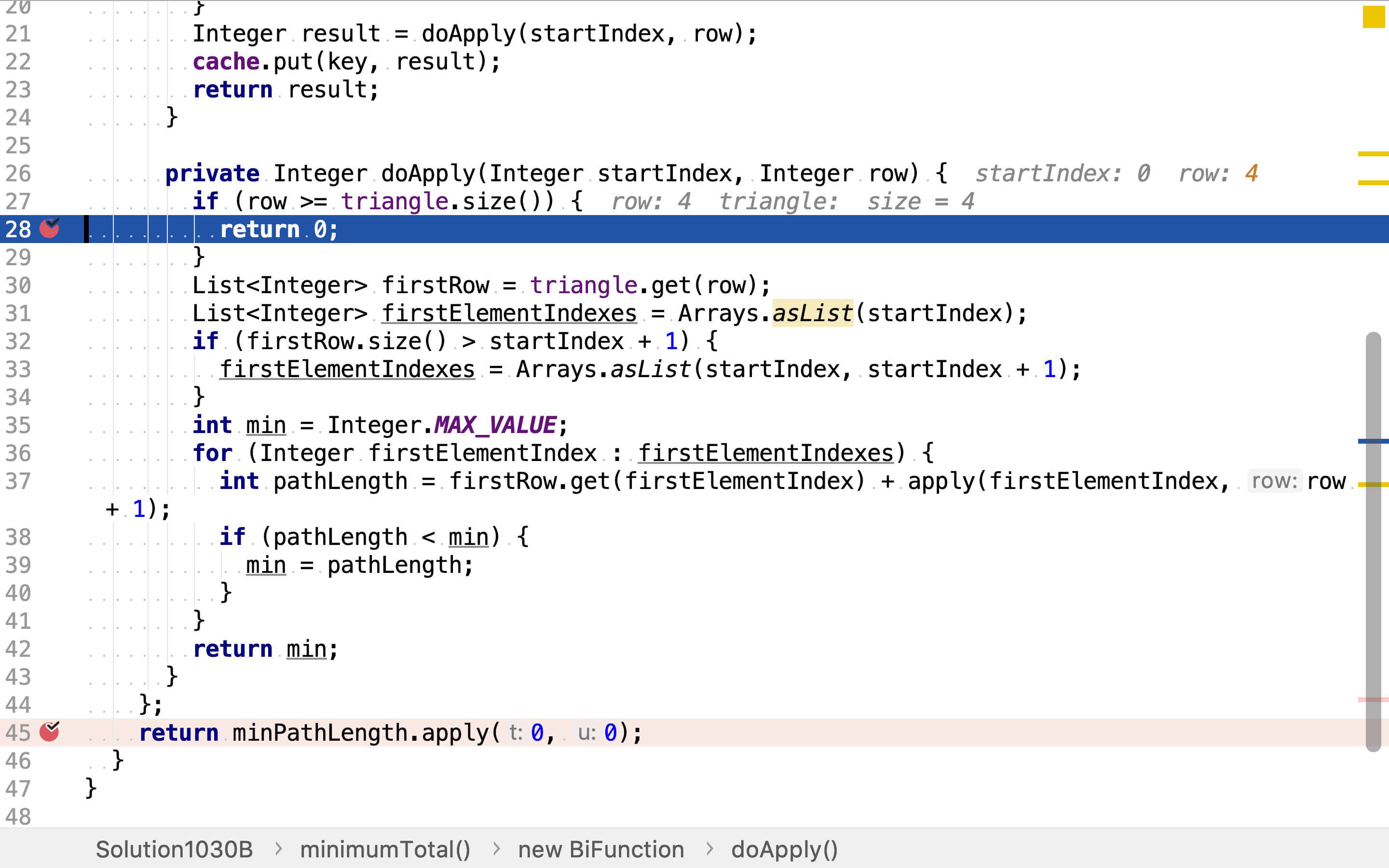
private Integer doApply(Integer startIndex, Integer row) {
if (row >= triangle.size()) {
return 0;
}
List<Integer> firstRow = triangle.get(row);
List<Integer> firstElementIndexes = Arrays.asList(startIndex);
if (firstRow.size() > startIndex + 1) {
firstElementIndexes = Arrays.asList(startIndex, startIndex + 1);
}
int min = Integer.MAX_VALUE;
for (Integer firstElementIndex : firstElementIndexes) {
int pathLength = firstRow.get(firstElementIndex) + apply(firstElementIndex, row + 1);
if (pathLength < min) {
min = pathLength;
}
}
return min;
}
};
return minPathLength.apply(0, 0);
}
}
定义一个递归函数minPathLength,其返回以某一点为三⻆形的顶点到底部的最短路径。
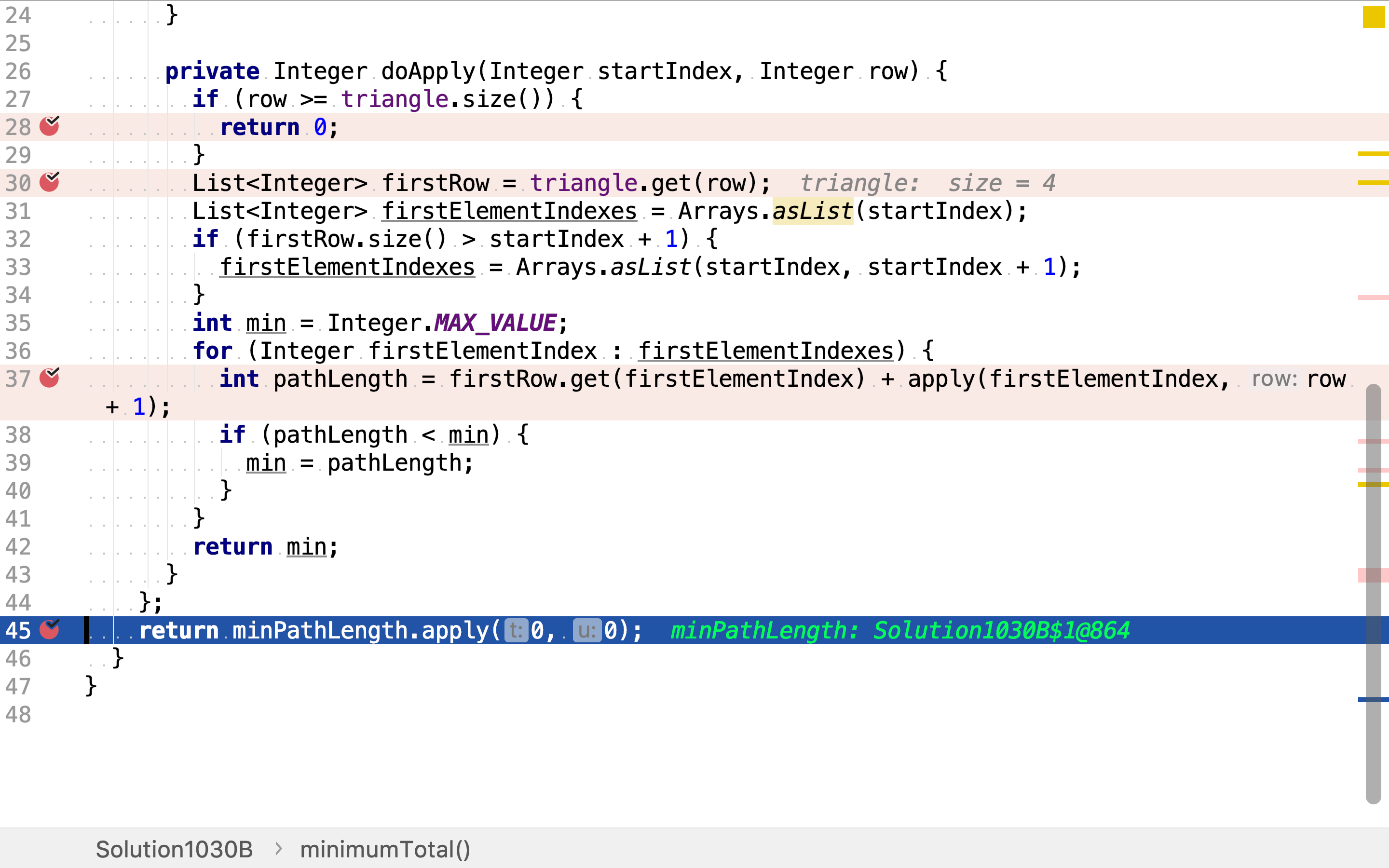
minPathLength用递归的方式求解问题。其先将三⻆形拆分为第一行和其余行。先求解第一行的解(第一行的解有两个,三⻆形中每一个点都与下方的两个点相邻)。
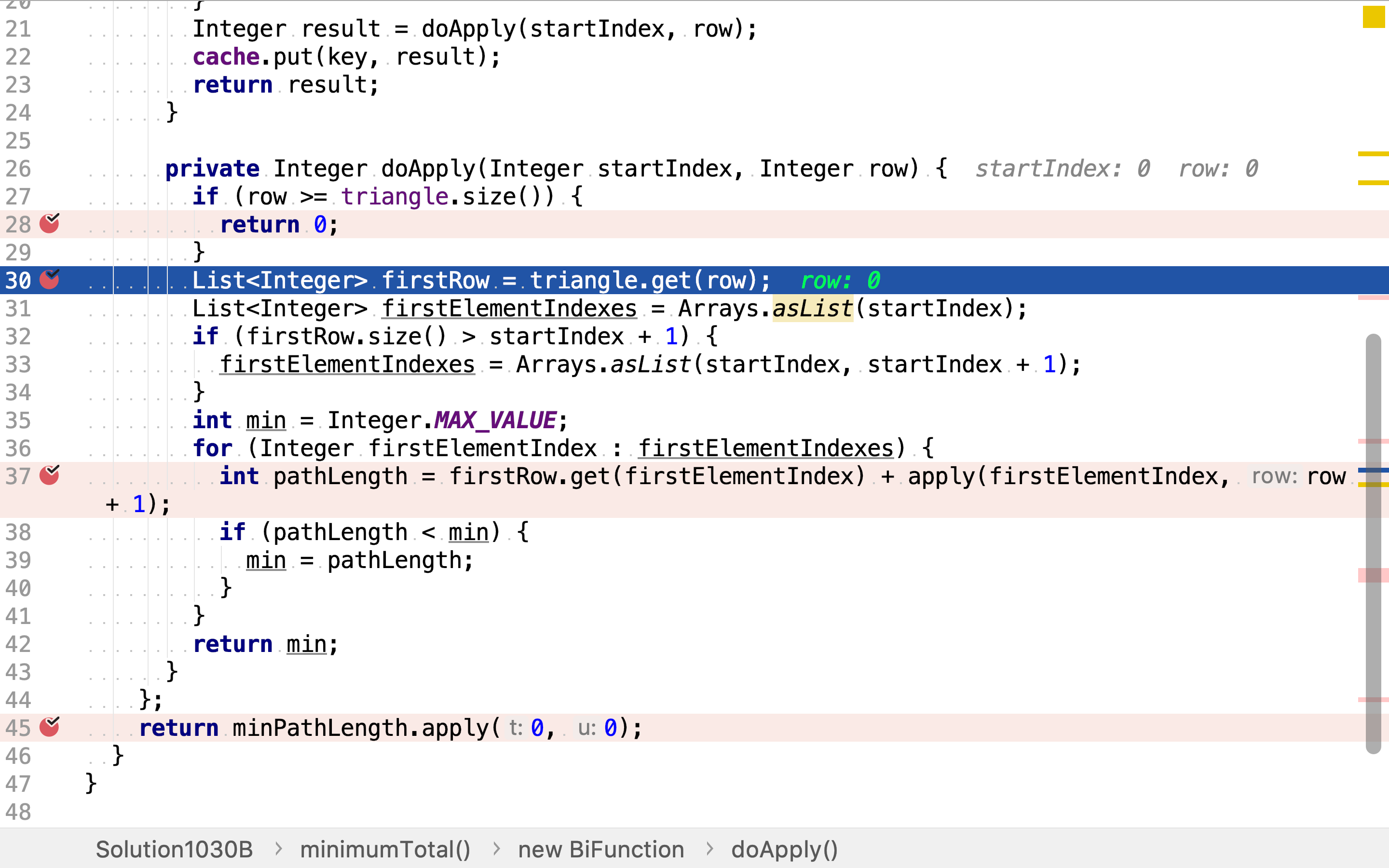
再求解其余行中的最短路径和。其余行中路径的起点由第一行的解决定。而第一行的解有两个,所以其余行中的解也分别有两个。
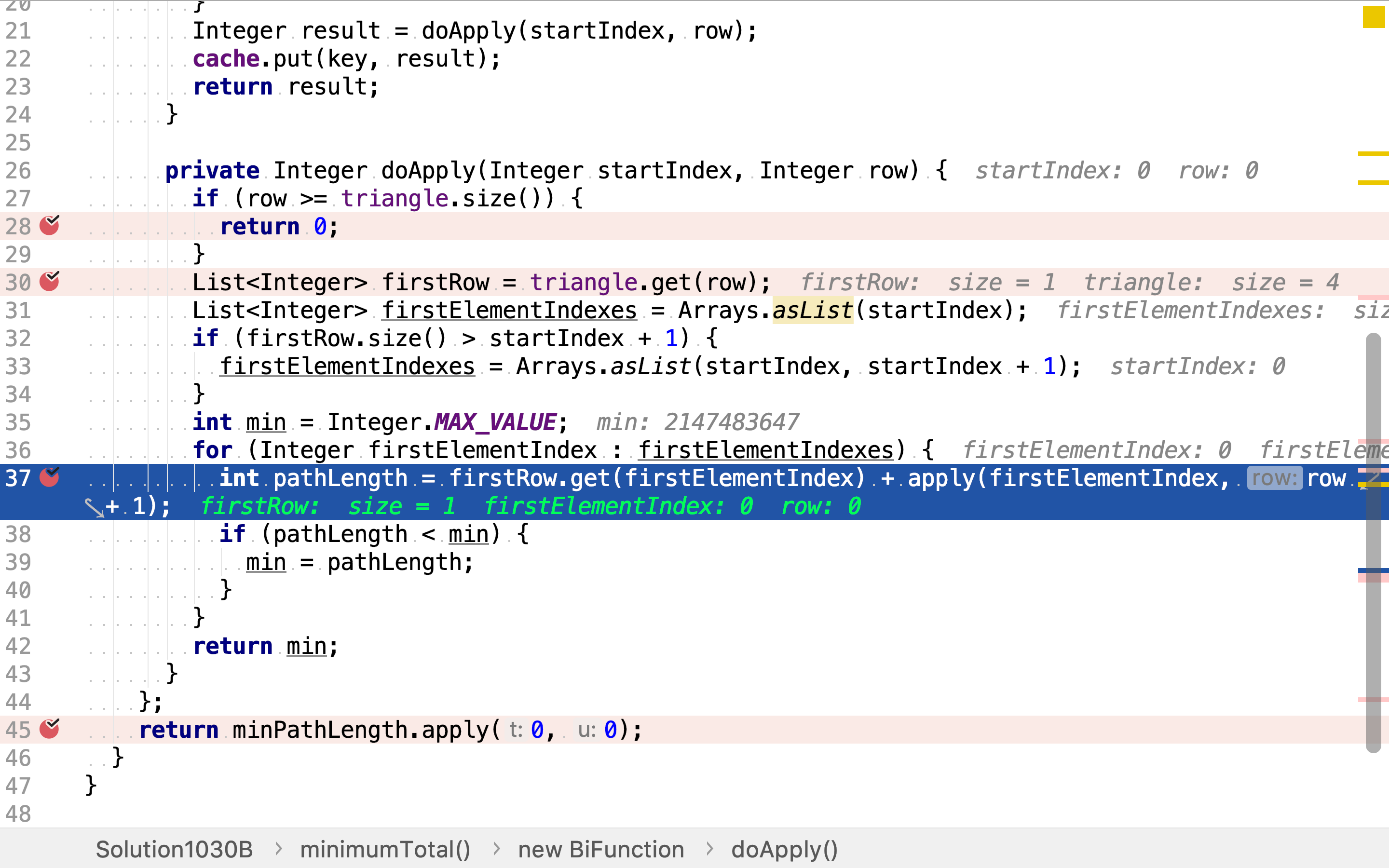
递归的终止条件为到达三⻆形的底部(访问过了最下面的一行)。
其暂存所有输入值对应的解,避免了重复计算。
复杂度分析
时间复杂度
minPathLength暂存了值,所以其实际的计算次数为n(n为三⻆形中点的数量。
时间复杂度为:
空间复杂度
minPathLength为三⻆形中每个点都暂存了结果,所以空间复杂度为:
一次遍历实现动态规划
上述动态规划演算法可以用面向过程的方式实现。
代码
package io.github.rscai.leetcode.bytedance.dynamic;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class Solution1030C {
public int minimumTotal(List<List<Integer>> triangle) {
List<List<Integer>> minPathLengths = new ArrayList<>();
for (List<Integer> row : triangle) {
minPathLengths.add(Collections.emptyList());
}
for (int rowIndex = triangle.size() - 1; rowIndex >= 0; rowIndex--) {
List<Integer> row = triangle.get(rowIndex);
List<Integer> minPathLength = new ArrayList<>();
if (rowIndex >= triangle.size() - 1) {
for (Integer value : row) {
minPathLength.add(value);
}
} else {
for (int indexOnRow = 0; indexOnRow < row.size(); indexOnRow++) {
minPathLength.add(row.get(indexOnRow) + Math
.min(minPathLengths.get(rowIndex + 1).get(indexOnRow),
minPathLengths.get(rowIndex + 1).get(indexOnRow + 1)));
}
}
minPathLengths.set(rowIndex, minPathLength);
}
return minPathLengths.get(0).get(0);
}
}
首先,构造一个跟轮入三⻆形相同尺寸的二维列表,用来存储以相应点为起点的最短路径和。
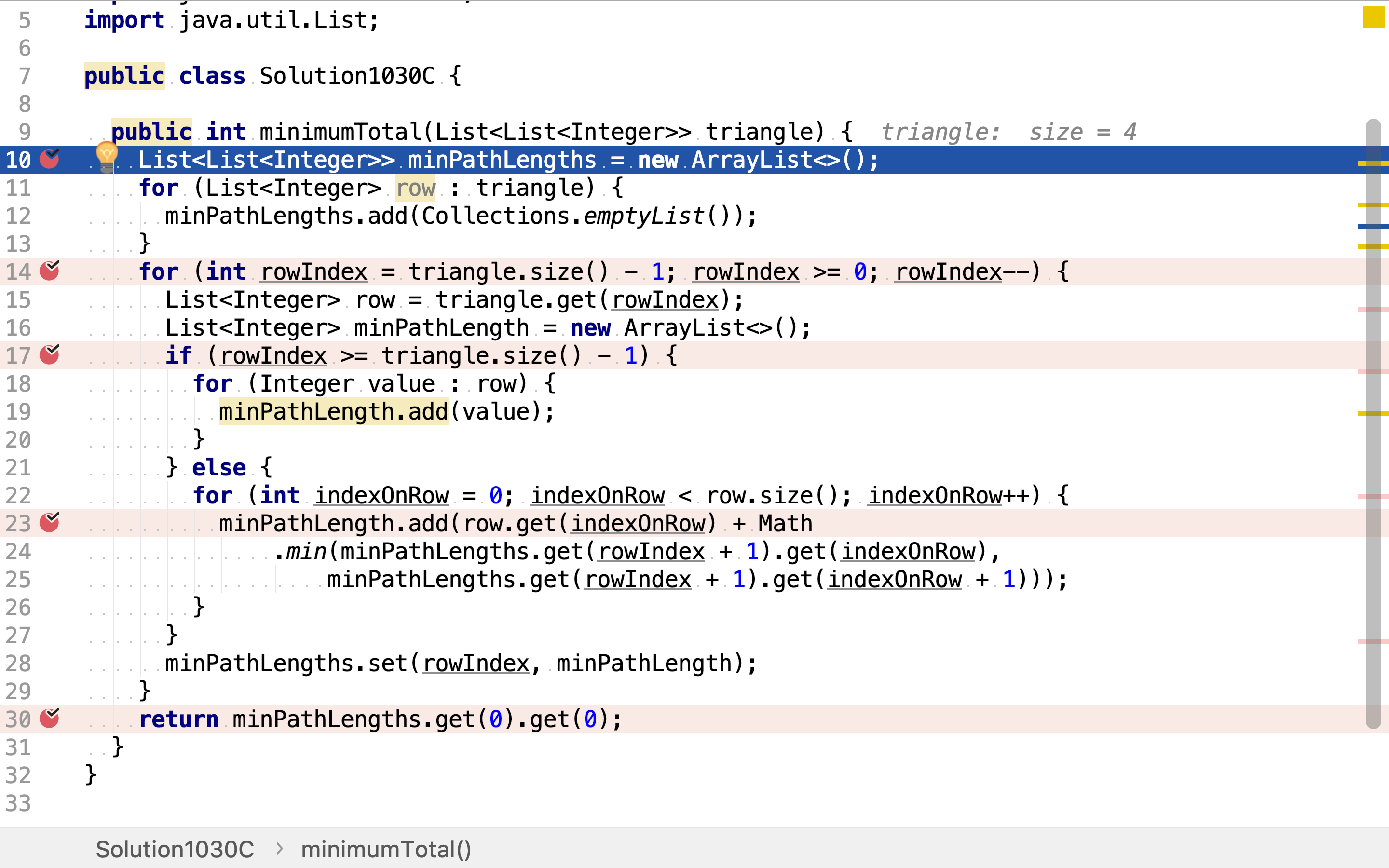
然后,从下往上计算。计算以每个点为起点,其最短路径和。
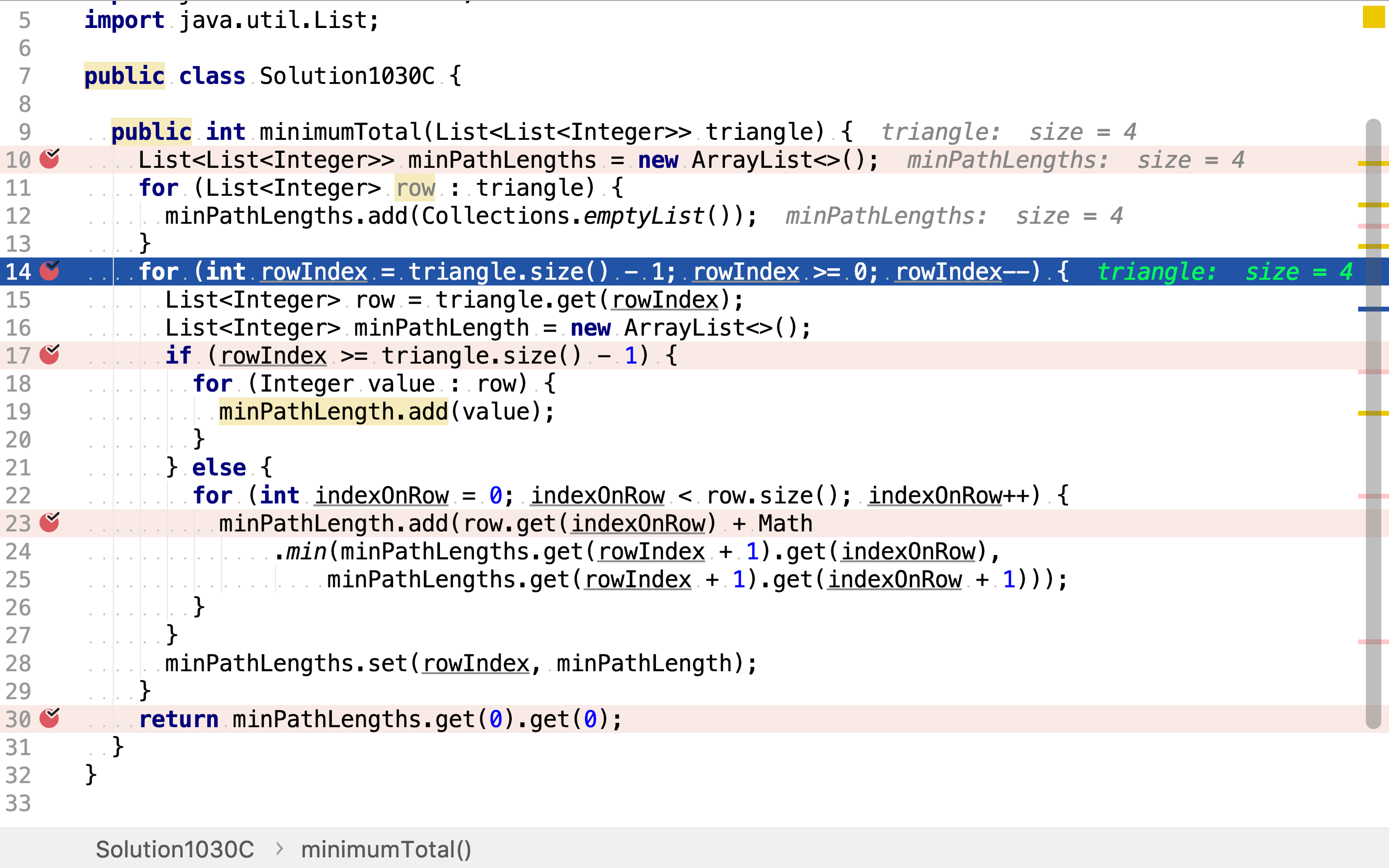
计算最短路径和时,有两种情形。第一种情形,当前行为最后一行,则以某个点为起点的唯一路径就是仅包含自身的列表,也就是最短路径。
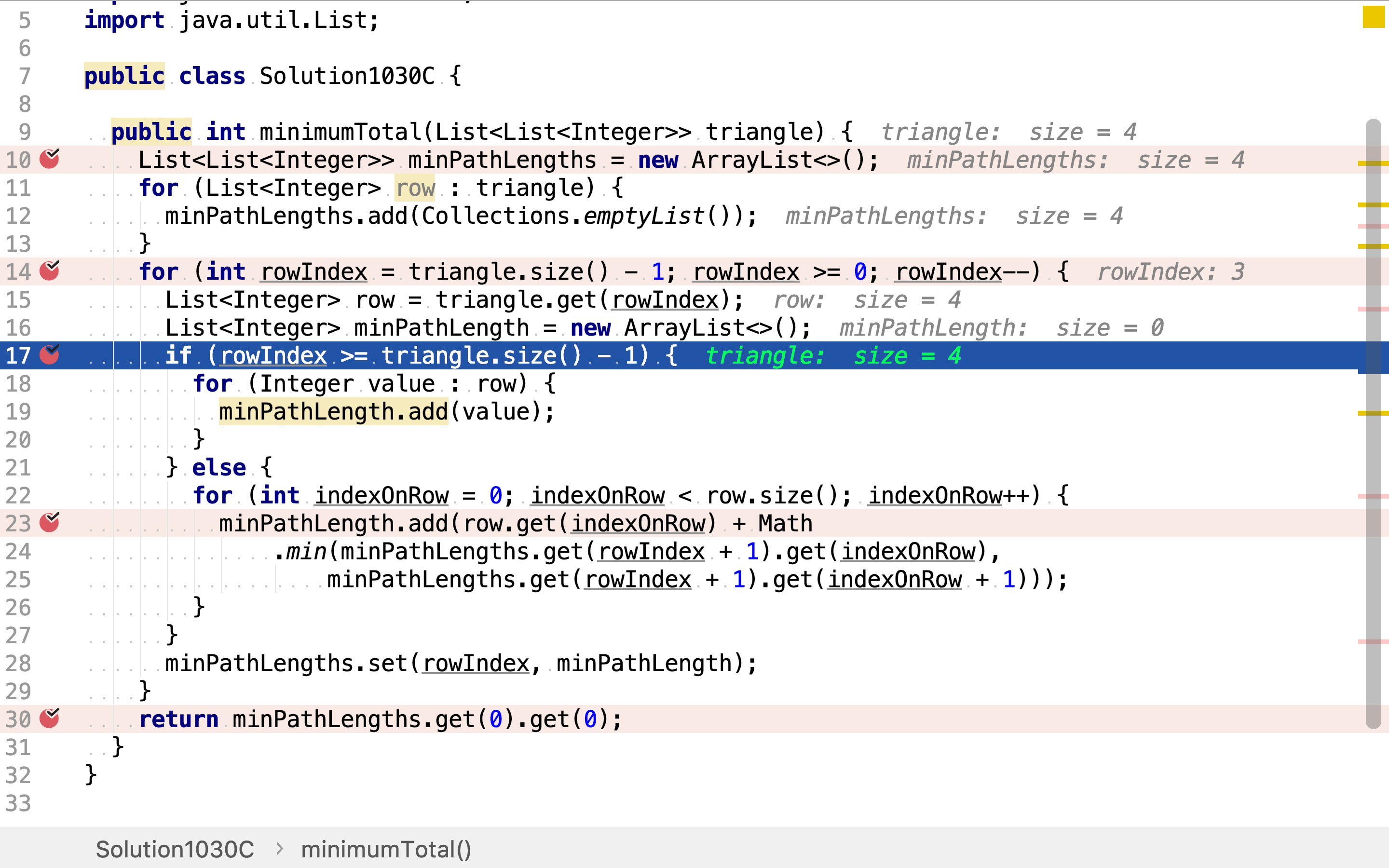
另一种情形,当前行不是最后一行。则以其上某一点为起点的最短路径和为:以相邻点为起点的最短路径加中最短的加上自身值。
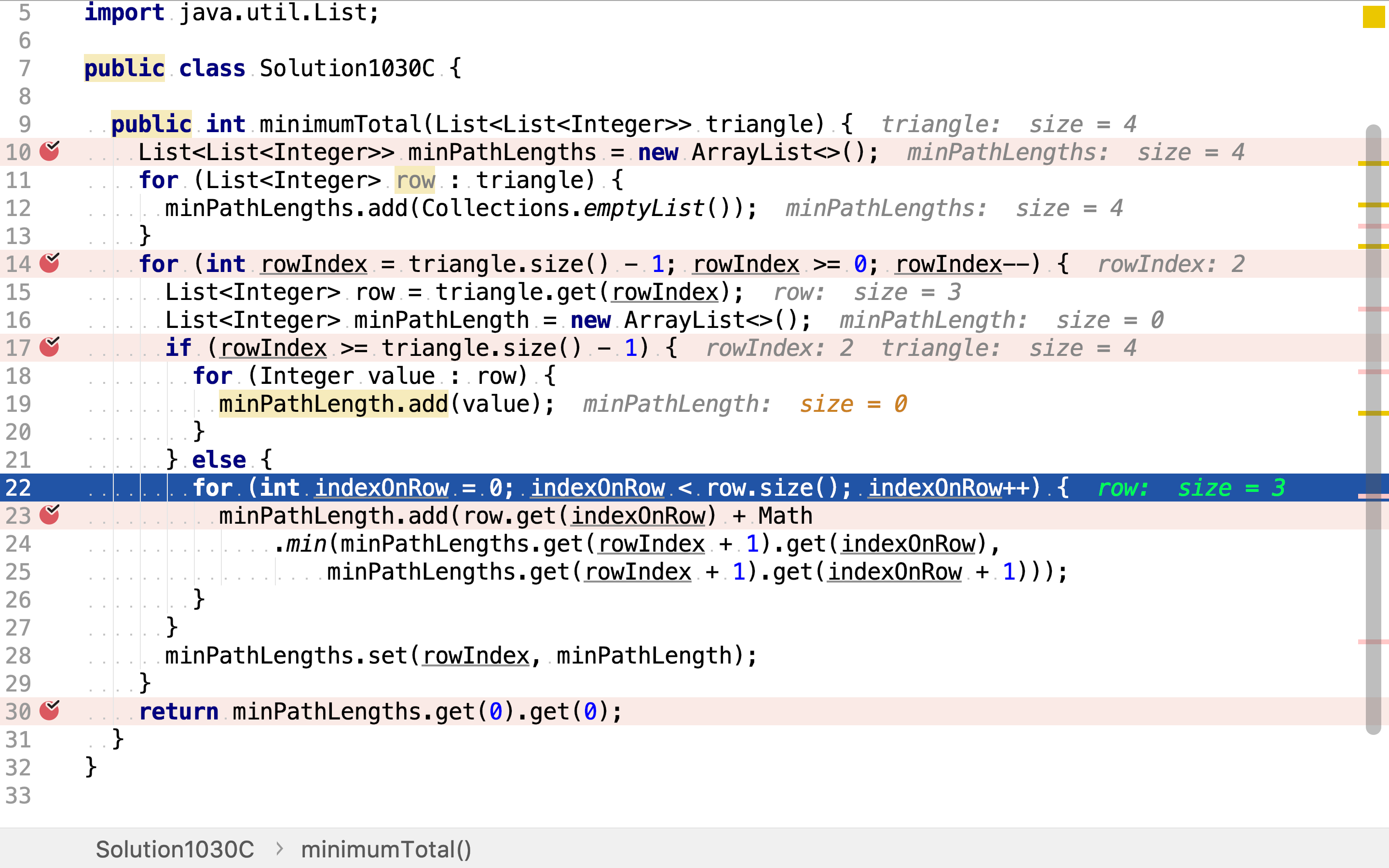
最后,再取出以全局三⻆形顶点为起点的最短路径和。
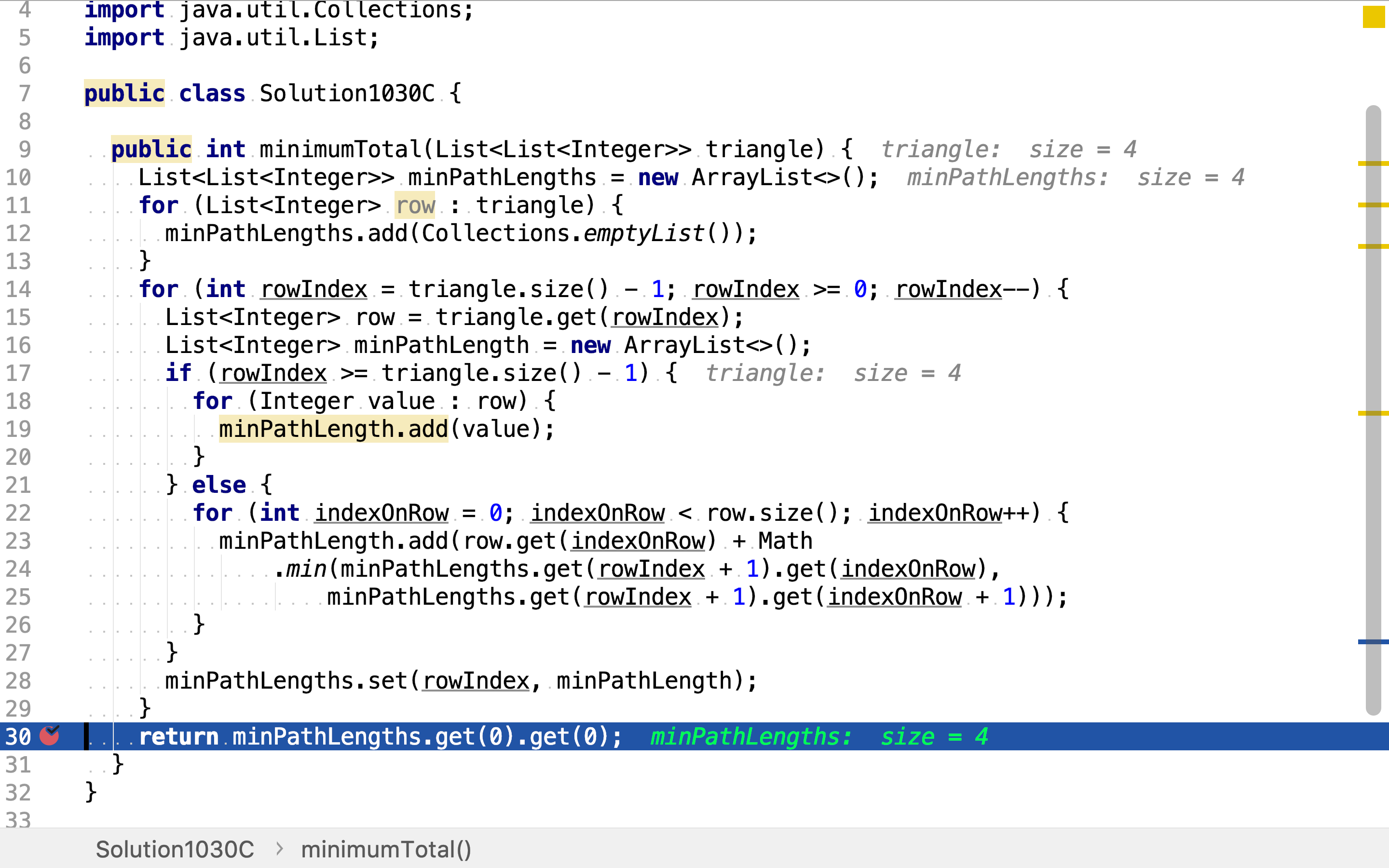
复杂度分析
时间复杂度
与用函数式实现的演算法相同。
空间复杂度
其为三⻆形中每个点都暂存了结果,所以空间复杂度为:


















