x的平方根

题目

实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例 1
输入: 4
输出: 2
示例 2
输入: 8
输出: 2
说明: 8 的平方根是 2.82842...,
    由于返回类型是整数，小数部分将被舍去。

牛顿法

在数学中，一个数 $x$ 的平方根 $y$ 指的是满足 $y^2 = x$ 的数，即平方结果等于 $x$ 的数。例如，4和-4都是16的平方根，因为 $4^{2}=(-4)^{2}=16$ 。

任意非负实数都有唯一的非负平方根，称为主平方根或算术平方根（英语：principal square root），记为 ${\sqrt {x}}$ ，其中的符号√称作根号。例如，9的主平方根为3，记作 ${\sqrt {9}}=3$ ，因为 $3^{2}=3\times 3=9$ 并且3非负。被求平方根的数称作被开方数（英语：radicand），是根号下的数字或者表达式，即例子中的数字9。

正数 $x$ 有两个互为相反数的平方根：正数 ${\sqrt {x}}$ 与负数 $-\sqrt x$ ，可以将两者一起记为 $\pm {\sqrt {x}}$ 。

负数的平方根在复数系中有定义。而实际上，对任何定义了开平方运算的数学对象都可考虑其「平方根」（例如矩阵的平方根）。

正数的平方根

若正整数x是平方数，则其平方根是整数。若正整数x不是平方数，则其平方根是无理数。

计算方法

长除式算法

长除式算平方根的方式也称为直式开方法，原理是 $(a+b)^2=a^2+2ab+b^2=a^2+(2a+b)b$ 。

首先将要开平方根的数从小数点分别向右及向左每两个位一组分开，如98765.432内小数点前的65是一组，87是一组，9是一组，小数点后的43是一组，之后是单独一个2，要补一个0而得20是一组。如1 04.85 73得四组，顺序为1' 04. 85' 73'。

将最左的一组的数减去最接近又少于它的平方数，并将该平方数的开方（应该是个位数）记下。

将上一步所得之差乘100，和下一组数加起来。

将记下的数乘20，然后将它加上某个个位数，再乘以该个个位数，令这个积不大于但最接近上一步所得之差，并将该个个位数记下，且将上一步所得之差减去所得之积。

记下的数一次隔两位记下。

重覆第3步，直到找到答案。

可以在数字的最右补上多组的00'以求得理想的精确度为止。

牛顿法

如果要求 $S\,(S>1)$ 的平方根，选取 $1\,<\,x_0\,<\,S$

$x_{n+1} = \frac{1}{2}\left(x_n + \frac{S}{x_n}\right)$ 例子：求 $\sqrt{125348}$ 至6位有效数字。

$\begin{aligned} x_0 &= 3^6 = 729.000 \\ x_1 &= \frac{1}{2} \left(x_0 + \frac{S}{x_0}\right) = \frac{1}{2} \left(729.000 + \frac{125348}{729.000}\right) = 450.472 \\ x_2 &= \frac{1}{2} \left(x_1 + \frac{S}{x_1}\right) = \frac{1}{2} \left(450.472 + \frac{125348}{450.472}\right) = 364.365 \\ x_3 &= \frac{1}{2} \left(x_2 + \frac{S}{x_2}\right) = \frac{1}{2} \left(364.365 + \frac{125348}{364.365}\right) = 354.191 \\ x_4 &= \frac{1}{2} \left(x_3 + \frac{S}{x_3}\right) = \frac{1}{2} \left(354.191 + \frac{125348}{354.191}\right) = 354.045 \\ x_5 &= \frac{1}{2} \left(x_4 + \frac{S}{x_4}\right) = \frac{1}{2} \left(354.045 + \frac{125348}{354.045}\right) = 354.045 \end{aligned}$

代码实现

package io.github.rscai.leetcode.bytedance.bonus; public class Solution1045A { public int mySqrt(int x) { if (x == 0) { return 0; } if (x == 1) { return 1; } double xn = 0; double xn1 = x/2; while (Math.abs(xn1 - xn) > 1e-12) { xn = xn1; xn1 = (xn + (double) x / xn) / 2.0; } return (int) xn1; } }

当轮入整数是0或1时，可以直得出其平方根。

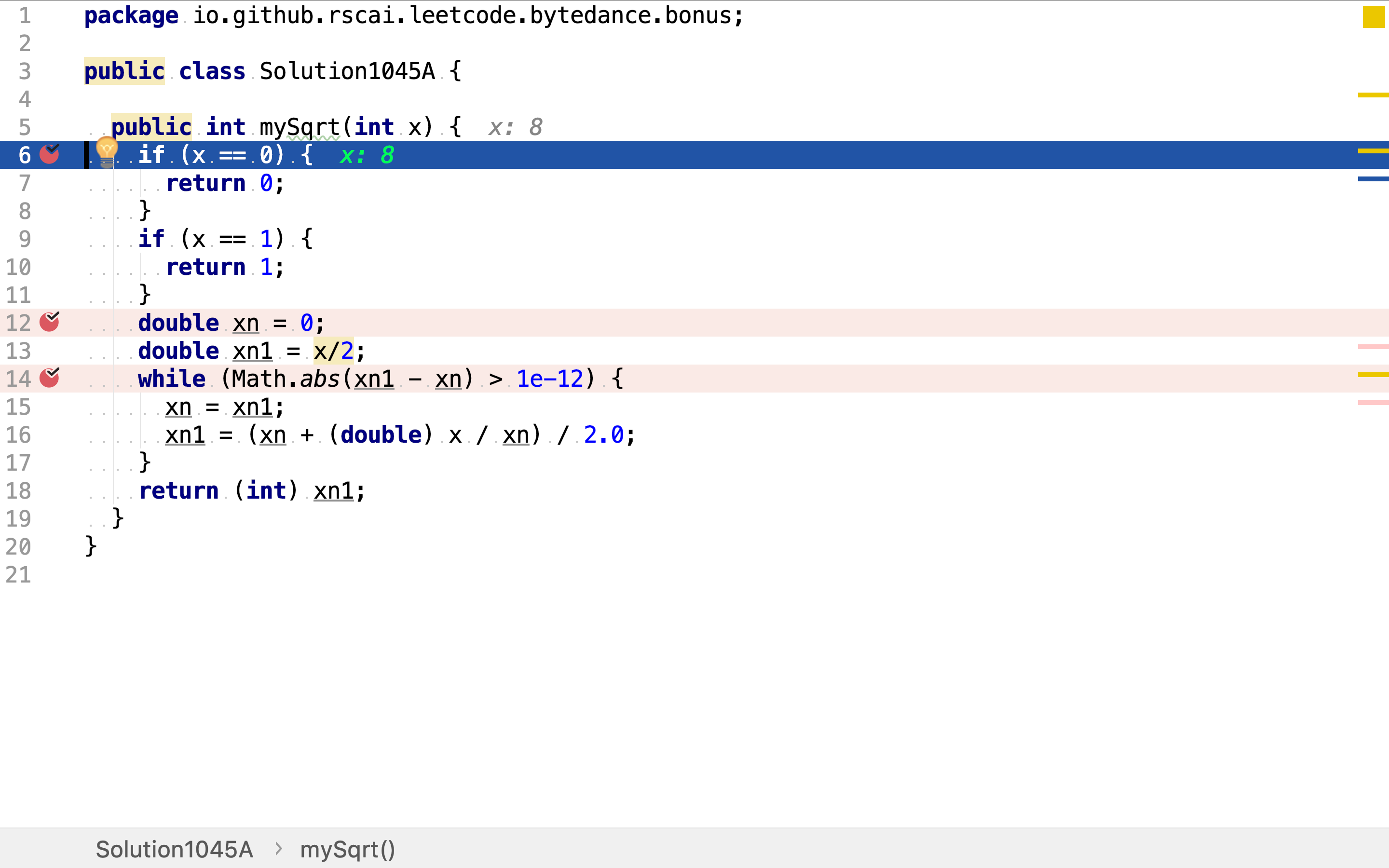
牛顿法是在连续函数上逐步逼近，所以将中间变量定义为较大取值范围的double。

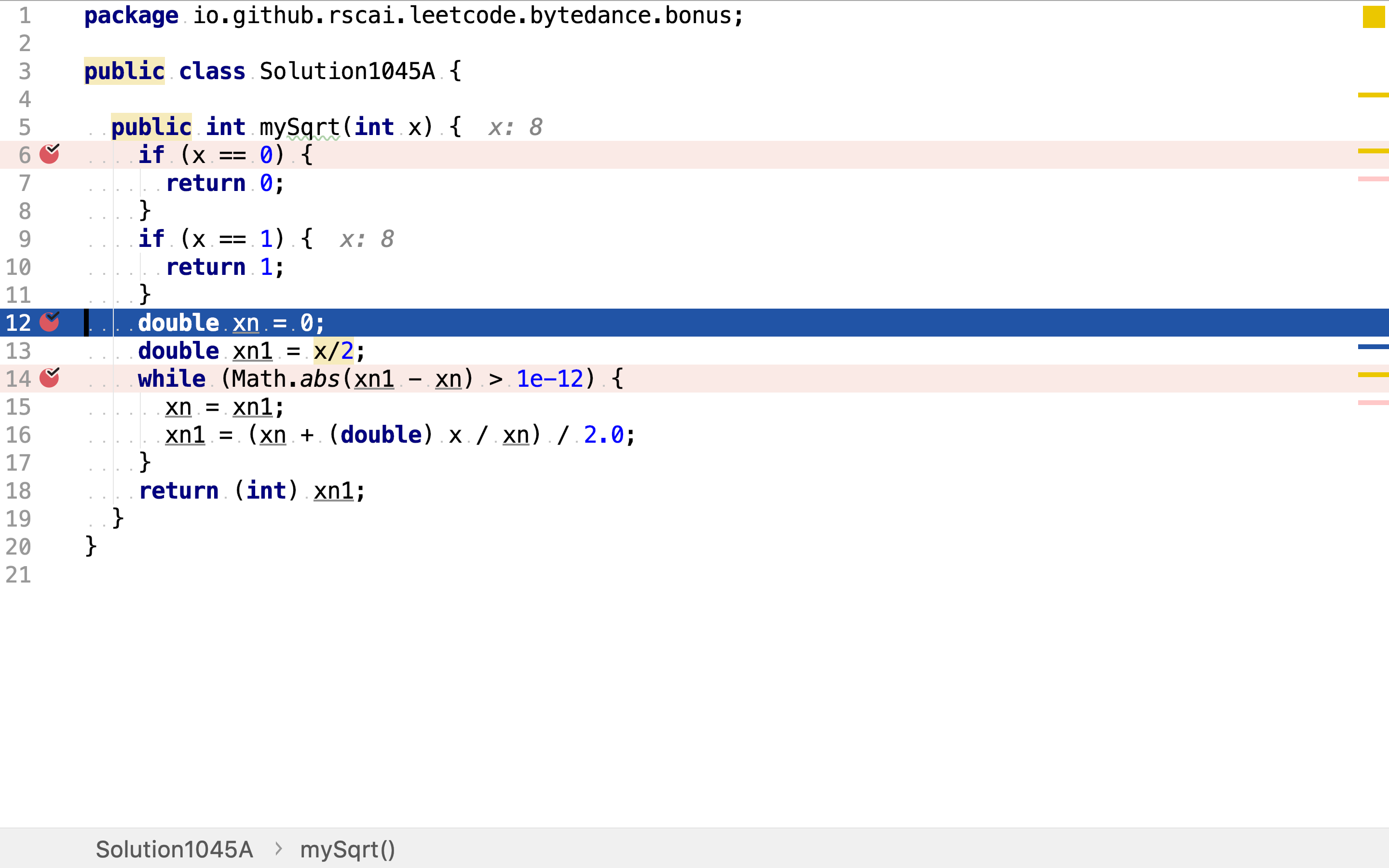
已知除了平方数，其它正整数的平方根都是无理数。所以，牛顿法只能通过不断迭代不断逼近平方根。实际实现中必须要有迭代中止条件，此处我们当前后两次迭代结果相差小于1e-12即中止迭代。

复杂度分析

时间复杂度

理论上讲，牛顿法时间复杂度是 $\mathcal{O}(\log n)$ 。但其实际表现取决于初始值的选择和迭代中止条件（Tolerance）的选择。

请参考：

空间复杂度

使用了两个变量xn, xn1，空间复杂度为 $\mathcal{O}(1)$ 。

二分搜索法

根据平方根定义，大于1的正整数平方根x是一个大于1小于S的实数。而本题只求平方根的整数部份，实际上就是求1至平方根x之间最大的整数。1至平方根x之间的整数是有限及有序的，二分搜索法可有效地在有限有序序列中搜索目标值。

步骤：

将1至S的整数序列切分为二
若中间值的平方小于或等于S，则继续在右半段序列中搜索：若中间值的平方大于S，则继续在左半段序列中搜索
当序列片断仅为一个整数时，其就是所求目标值

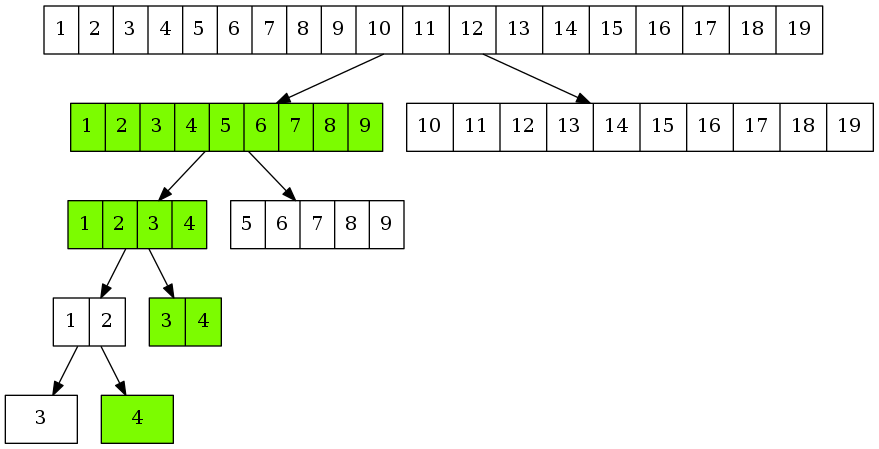
举个例子，求20的平方根的整数部份。20的平方根肯定是1至20之间，20平方根的整数部份一定是1至20之间19个整数中的一个。

将序列1,2,...,18,19二分为1,2,...,9和10,...,19，中间值10的平方100大于20，继续在左半段搜索
将左半段序列1,2,...,18,19二分为1,2,3,4和5,6,7,8,9，中间值5的平方25大于20，继续在左半段搜索 3.将左半段序列1,2,3,4二分为1,2和3,4，中间值3的平方9小于20，继续在右半段中搜索
将右半段序列3,4二分为3和4，中间值4的平方16小于20，继续在右半段中搜索
右半段4仅有一个整数，所以4就是所求值

代码实现

package io.github.rscai.leetcode.bytedance.bonus; public class Solution1045B { public int mySqrt(int x) { if (x == 0) { return 0; } if (x == 1) { return 1; } int start = 1; int end = x; while (end - start != 1) { long mid = (end + start) / 2; if ((mid * mid) <= x) { start = (int) mid; } else { end = (int) mid; } } return start; } }

先处理一些简单的情况，如输入整数是0或1。

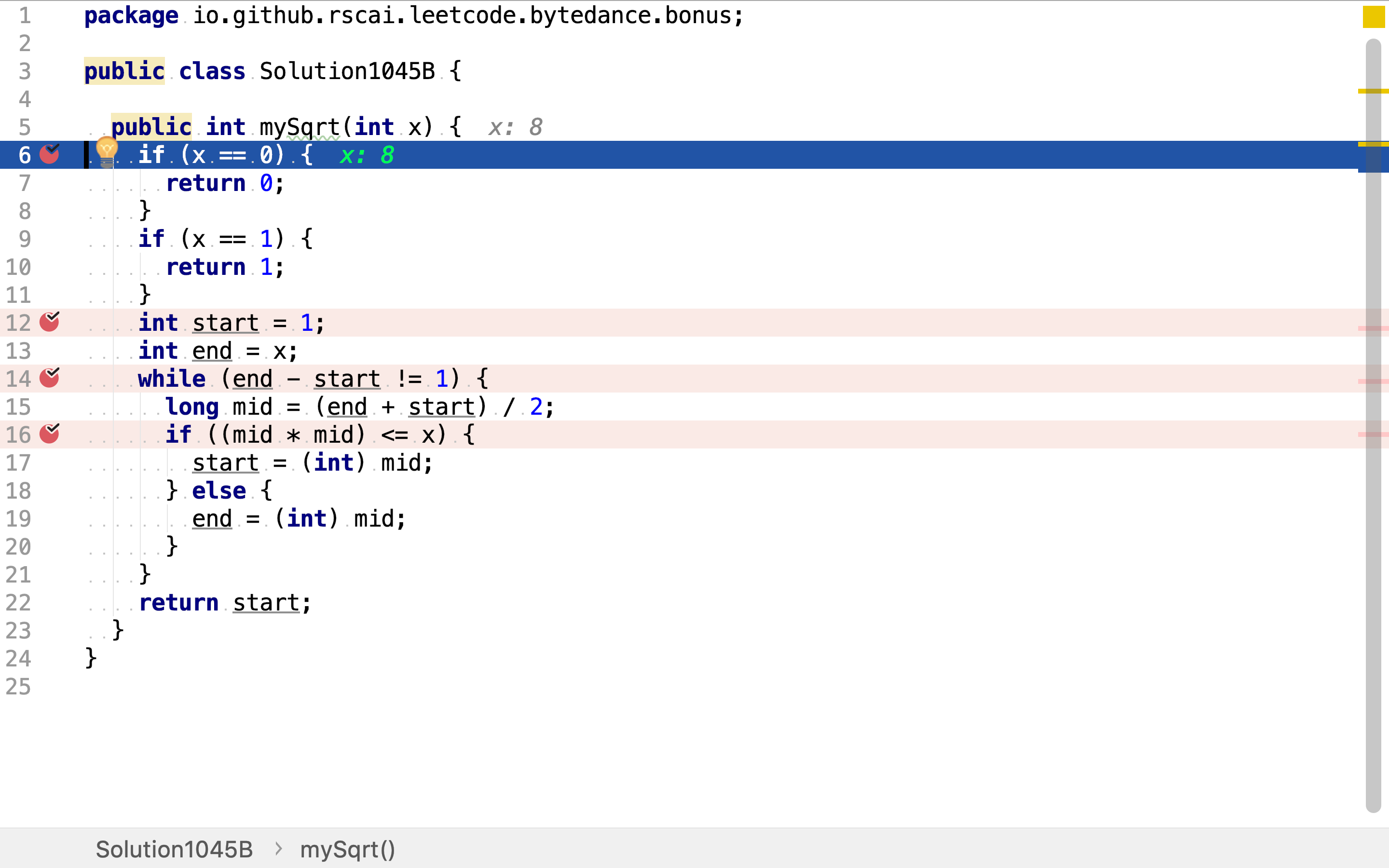
整数序列的起止初始为1和轮入整数，区间使用左闭右开模式。

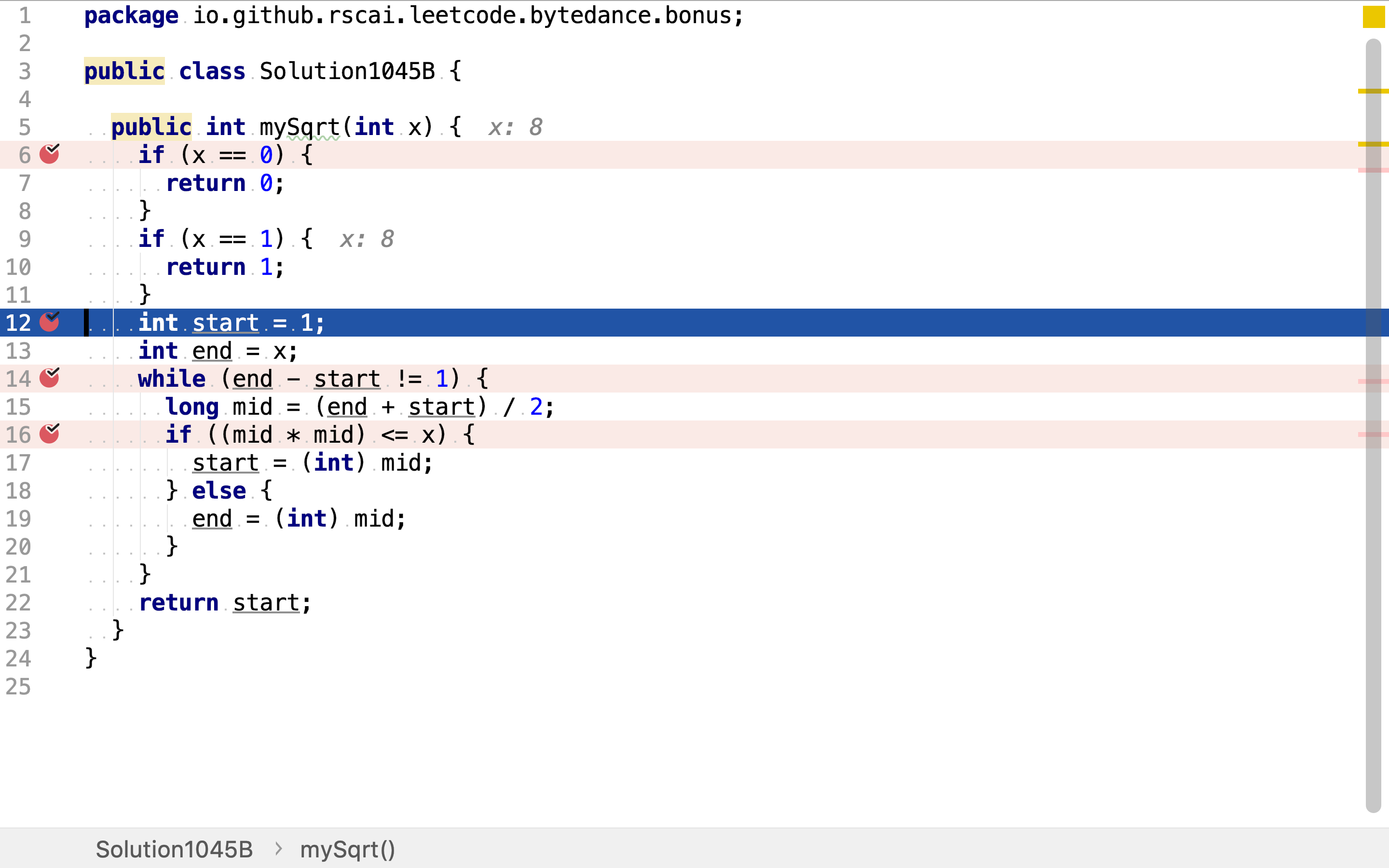
二分搜索法是一种递归方法，这𥚃使用while循环实现递归。递归中止条件为整数序列仅包含一个整数。

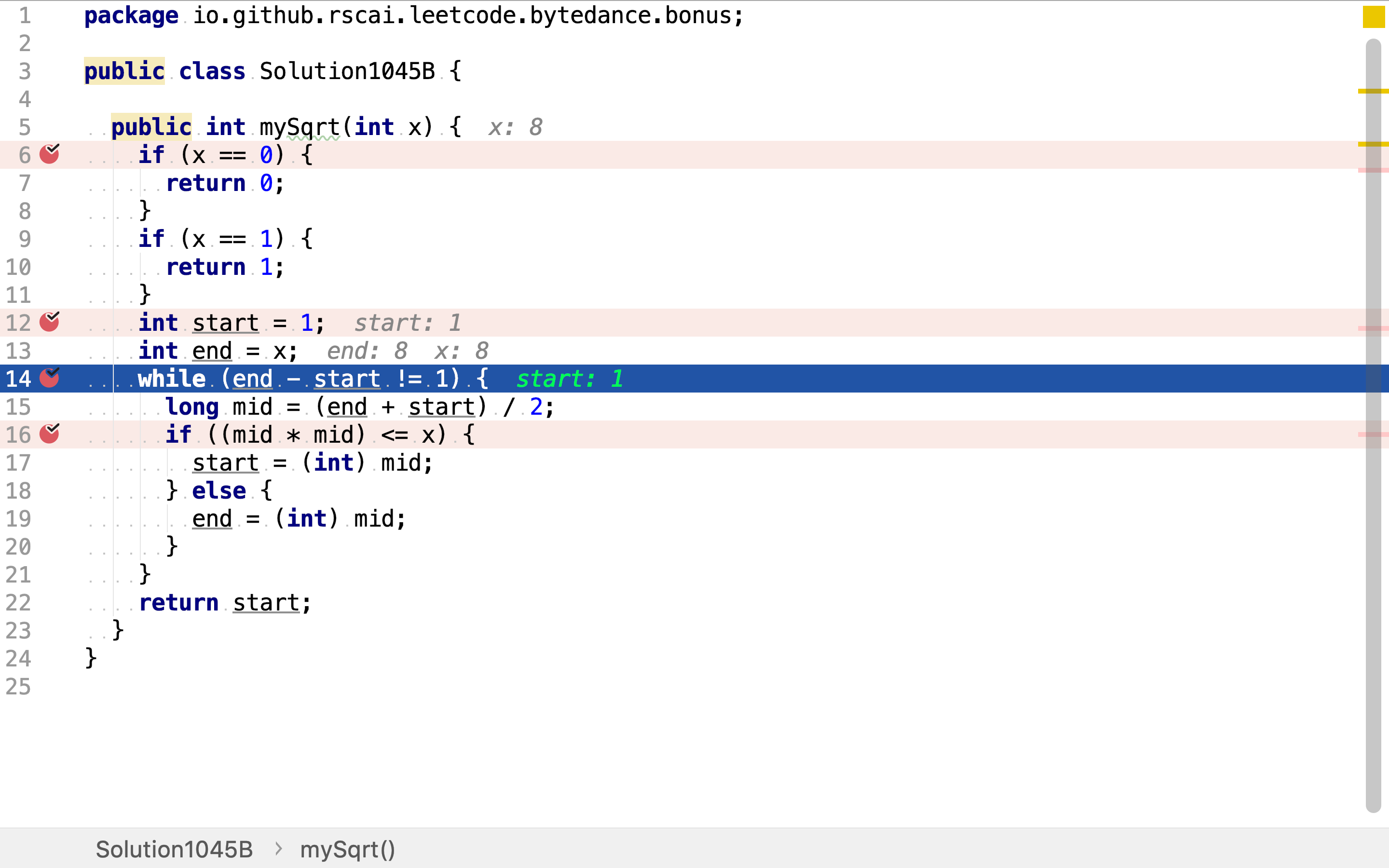
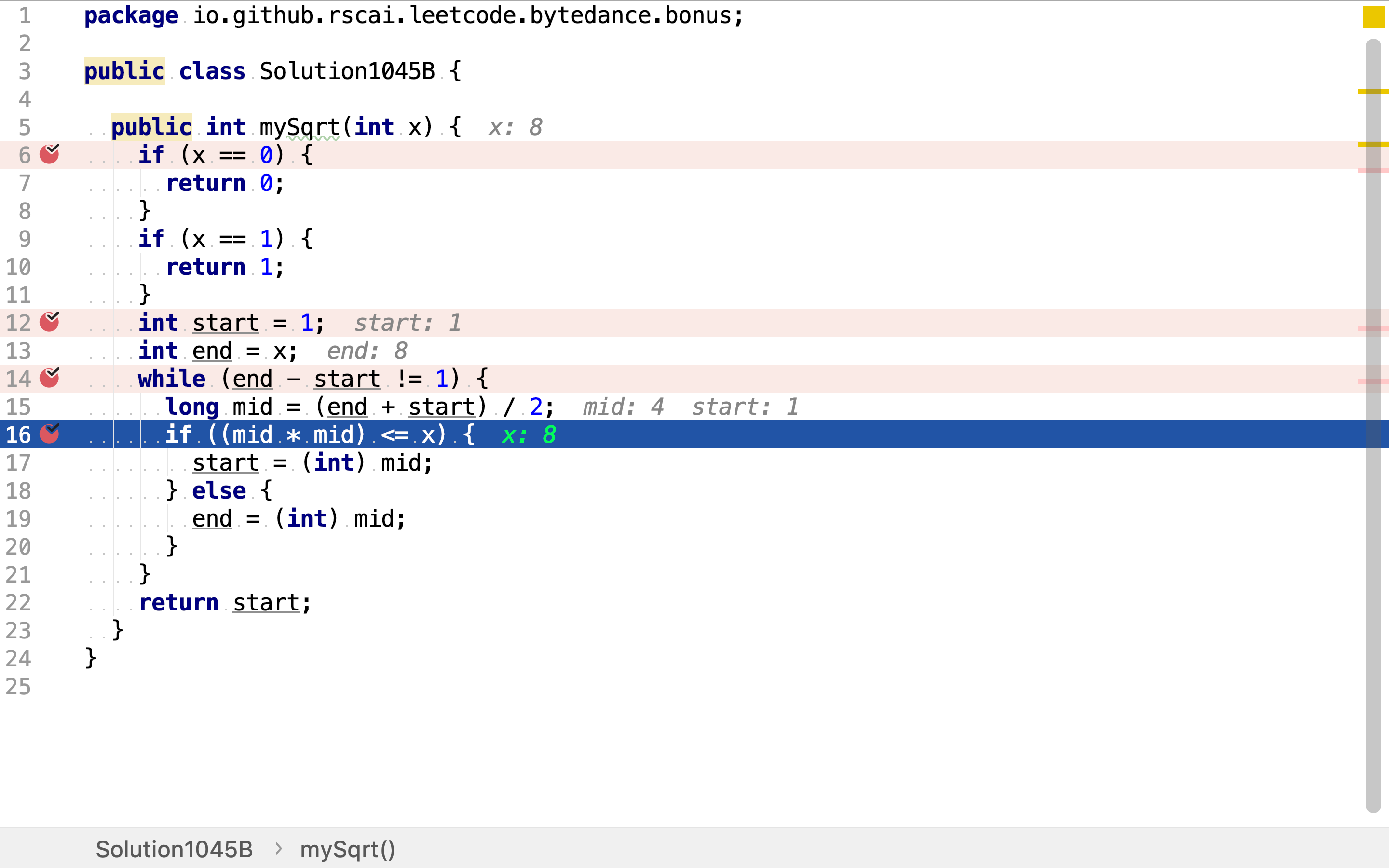
将整数序列不断地二分，通过中间值平方和输入值之间的大小关系，判断目标值是在左半段序列或是在右半段序列。