Lisp-like tree representation

题目

There is a particular notation for multiway trees in Lisp. Lisp is a prominent functional programming language, which is used primarily for artificial intelligence problems. As such it is one of the main competitors of Prolog. In Lisp almost everything is a list, just as in Prolog everything is a term.

The following pictures show how multiway tree structures are represented in Lisp.

Note that in the "lispy" notation a node with successors (children) in the tree is always the first element in a list, followed by its children. The "lispy" representation of a multiway tree is a sequence of atoms and parentheses '(' and ')', which we shall collectively call "tokens". We can represent this sequence of tokens as a Prolog list; e.g. the lispy expression (a (b c)) could be represented as the Prolog list ['(', a, '(', b, c, ')', ')']. Write a predicate tree_ltl(T,LTL) which constructs the "lispy token list" LTL if the tree is given as term T in the usual Prolog notation.

Example: ?- tree_ltl(t(a,[t(b,[]),t(c,[])]),LTL). LTL = ['(', a, '(', b, c, ')', ')']

As a second, even more interesting exercise try to rewrite tree_ltl/2 in a way that the inverse conversion is also possible: Given the list LTL, construct the Prolog tree T. Use difference lists.

用单元测试描述为：

解题思路

多路树的形态可以被归纳为以下几种：

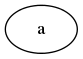
1. 只有一个节点，如下图。这类多路树在Lisp中表示为一个原子a。

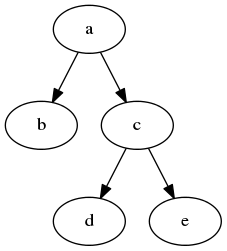
1. 除了根节点，还拥有一至多个子树，如下图，这类多路树在Lisp中表示为一个列表，其中第一个原子为根节点，子树紧随其后。而每一棵子树又都是多路树，其形态也属必于1、2两种之一。

所以，我们可以归纳出以下转换规则：

1. 若多路树没有子树则转换为[a]，其中[a]为根节点值。
2. 若多路树有子树则转换为['(', a, <subtree1>, <subtree2>, ..., ')']，其中a为根节点值，<subtree1>为第一棵子树转换后的值，为第二棵子树转换后的值，依次类推。subtree的数量与子树数量相同。而子树的转换规则则套用1和2，因为子树都是多路树。

举个例子，给定多路树(a,[(f,[(g,[])]),(c,[]),(b,[(d,[]),(e,[])])])。

• 此多路树拥有子树，套用规则2。先转换子树
  • 转换第一棵子树(f,[(g,[])])
    • 此树拥有子树，套用规则2。先转换子树
      • 转换第一棵子树(g,[])
        • 此树没有子树，套用规则1。转换为[g]
    • 拼接转换后的子树和根节点及括号，得到['(', f, g, ')']
  • 转换第二棵子树(c,[])
    • 此树没有子树，套用规则1。转换为[c]
  • 转换第三棵子树(b,[(d,[]),(e,[])])
    • 此树拥有子树，套用规则2。先转换子树
      • 转换第一棵子树(d,[])
        • 此树没有子树，套用规则1。转换为[d]
      • 转换第二棵子树(e,[])
        • 此树没有子树，套用规则1。转换为[e]
    • 拼接转换后的子树和根节点及括号，得到['(', b, d, e, ')']
• 拼接转换后的子树和根节点及括号，得到['(', a, '(', f, g, ')', c, '(', b, d, e, ')', ')']

代码实现：

reduce是Python标准库提供的一个函数式的工具，其声明为：

reduce(function, iterable, initializer)

其功能是将function累积地、从左往右作用于iterable中的每一个元素。

reduce相当于如下代码：

def reduce(function, iterable, initializer=None):
    it = iter(iterable)
    if initializer is None:
        value = next(it)
    else:
        value = initializer
    for element in it:
        value = function(value, element)
    return value

这𥚃，使用reduce拼接转换后的子树列表。

反过来，也可以从Lisp格式的多路树转换为Python格式多路树。

转换规则为：

1. 从列表中取出第一个元素，其若为原子则此树为单一节点多路树。
2. 从列表中取出第一个元素，其若为'('则略过取下一个元素为根节点元素。再从剩余列表中解拆出零至多个子树，直至遇到')'。

举个例子，给定以Lisp格式展示多路树的列表['(', 'a', '(', 'f', 'g', ')', 'c', '(', 'b', 'd', 'e', ')', ')']。

• 取出第一个元素为(，略过，取下一个元素a为根节点值
• 从剩余列表中解析出第一棵子树
  • 取出第一个元素为(，略过，取下一个元素f为根节点值
  • 从剩余列表中解析出第一棵子树
    • 取出第一个元素为原子（非括号字符），其是一棵仅有一个节点的多路树(g,[])
  • 从剩余列表中取出第一个元素为)，表明已触及多路树的末尾。至此，解析出了多路树(f,[(g,[])])
• 从剩余列表中解析出第二棵子树
  • 取出第一个元素为原子，其是一棵仅有一个节点的多路树(c,[])
• 从剩余列表中解析出第三棵子树
  • 从剩余列表中取出第一个元素为(，略过，取下一个元素b为根节点值
  • 从剩余列表中解析出第一棵子树
    • 取出第一个元素d是原子，其是一棵仅有一个节点的多路树(d,[])
  • 从剩余列表中解析出第二棵子树
    • 取出第一个元素e是原子，其是一棵仅有一个节点的多路树(e,[])
  • 从剩余列表中取出第一个元素为)，表明已触及多路树的末尾。至此，解析出了多路树(b,[(d,[]),(e,[])])
• 从剩余列表中取出第一个元素为)，表明已触及多路树的末尾。至此，解析出了多路树(a,[(f,[(g,[])]),(c,[]),(b,[(d,[]),(e,[])])])

代码实现：