Path from one node to another one
题目
Write a predicate path(G, A, B, P) to find an acyclic path P from node A to node B in the graph G. The predicate should return all paths via backtracking.
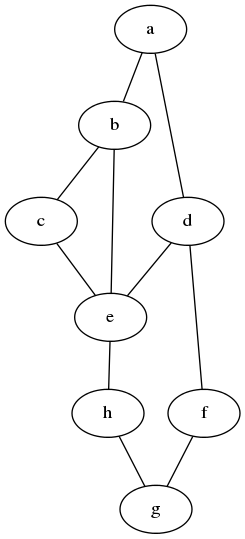
假设,给出如下图。从点d到点e之间的路径有:
d, ed, a, b, ed, a, b, c, ed, g, h, ed, f, g, h, e
解题思路
点到点之间的路径可以解构为一组有序的边,一条边的终止点即为后续边的起始点,且第一条边的起始点为路径的起始点,最后一条边的终止点为路径的终止点。例如路径d, a, b, e是由边[(d, a), (a, b), (b, e)]组成。
搜寻点到点之间的路径就可以转换为「搜寻一组首尾相连的边,且第一条边的起始点和最后一条边的终止点是所求路径起始点和终止点」。
举个例子,给定如下图,求点a至点e之间的路径。

- 首先从点
a出发,其有两条边,终止点分别是b和d。这𥚃先取边(a, b) - 然后从点
b出发,其有三条边,终止点分别是a,c和e。a已在路径中,不能回头。所以从c和e中取一。这𥚃取c。 - 再然后从点
c出发,其有两条边,终止点分别是b和e。b已大中弓土路径中,不能回头。所以取e。 - 到达终点。寻到路径
a, b, c, e。
点到点之间路径搜寻方法可以归纳为:
- 以起始点为出发点
- 从与出发点相邻的点(相连边的终止点)(但不包含在路径中)取一个点,加入路径。并以新的点为出发点,重复步骤2直至遇到目的点
以上方法可以找出一条路径,但本题要求找出所有的路径。所以,以上的方法需要将以修改。
假设,点到点之间的路径是一个由点组成的序列
序列上的每一位都有多个选项,而每一位的可选项都由前一位值决定。其所有组合可以用树的形式直观地展示。
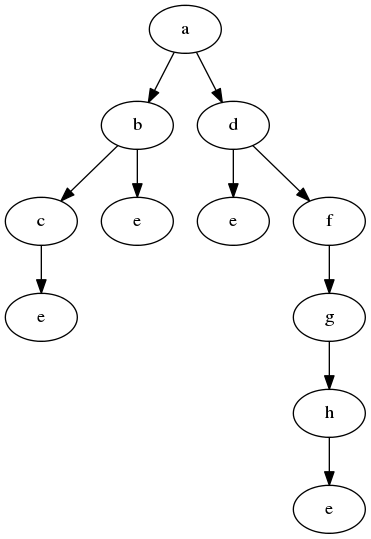
从a出发,有两个相邻点可选,分别是b和d。从b出发有两个相邻点可选,分别是c和e。从d出发有两个相邻点可选,分别是e和f。依此类推。。。
搜寻点到点之所有路径的方法可以归纳为:
- 从一点出发,罗列所有未在路径的相邻点
- 以每一个相邻点被出发点,套用步骤1和2,直至没有未在路径中的相邻点或到达目的点
代码实现:
def path(g, start, end):
paths = listPath(g, [start], start, end)
return [[start] + e for e in paths]
def listPath(g, path, current, end):
# it reach destination when current node is end one
if current == end:
return [[]]
nodes = nextNodes(g, path, current)
return [[nextNode]+remainPath for nextNode in nodes for remainPath in listPath(g, path+[nextNode], nextNode, end)]
def nextNodes(g, path, start):
for edge in g[1]:
if edge[0] == start and edge[1] not in path:
yield edge[1]
elif edge[1] == start and edge[0] not in path:
yield edge[0]
单元测试:
from python99.graph.p602 import path
def test_path():
assert path((['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h'],
[
('a', 'b'),
('a', 'd'),
('b', 'c'),
('b', 'e'),
('c', 'e'),
('d', 'e'),
('d', 'f'),
('d', 'g'),
('e', 'h'),
('f', 'g'),
('g', 'h')
]), 'a', 'e') == [
['a', 'b', 'c', 'e'],
['a', 'b', 'e'],
['a', 'd', 'e'],
['a', 'd', 'f', 'g', 'h', 'e'],
['a', 'd', 'g', 'h', 'e']
]