Construct all spanning trees

题目

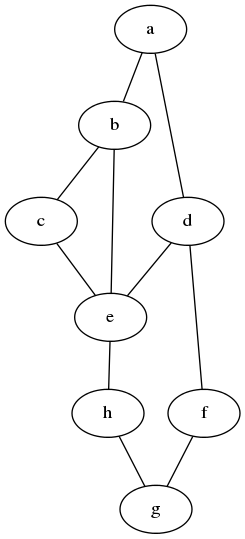
Write a predicate s_tree(Graph,Tree) to construct (by backtracking) all spanning trees of a given graph. With this predicate, find out how many spanning trees there are for the graph depicted to the left. The data of this example graph can be found in the file p6_04.dat. When you have a correct solution for the s_tree/2 predicate, use it to define two other useful predicates: is_tree(Graph) and is_connected(Graph). Both are five-minutes tasks!

生成树「spanning tree」

在图论中，无向图 G 的生成树（英语：Spanning Tree）是具有 G 的全部顶点，但边数最少的连通子图。

以 表示顶点， 表示边.若图 和树 ，有 和 ，那么 是 的生成树。

一个图的生成树可能有多个。

解题思路

罗列图的所有生成树

根据图和生成树的定义，可以得出以下定论：

  1. 当点数量为N时，连通所有点所需最少边数为N-1。图项形式由点列表和边列表组成，所以点数量N是已知的。
  2. 从边集合中取出N-1个边，如果言些边的起止点包含了所有的点，则这个边集合就是一根生成树。

所有生成树可以用以下方法获得：

  1. 通过点数量计算出生成树的边数量N
  2. 罗列出从所有边集合中取N条边的所有组合
  3. 过泸步骤2罗列出的组合，留下边的起止点包含了所有点的组合，即为图的所有生成树

组合

从大小为M集儳中取N个元素（M > N），所有可能的取法可以用回溯法「backtracking」求得。

用递归形式描述为：

将集合转换为有序列表，

  1. 从有序列表中取出一个元素
  2. 从第一步取出的元素之后的子列表中取出N-1个元素（套用步骤1和2，直至剩余列表长度等于要取的元素量N或N为0）

举个列子，有边集合[(a, b), (b, c), (c, d)]，从中取出两条边，列出所有的组合。

  • 从集合[(a, b), (b, c), (c, d)]中取出一条边，有三种选择
  • 取出(a, b)作为第一条边。再从剩余的[(b, c), (c, d)]中取出一条边，有两种选择
    • 取出(b, c)，组成组合[(a, b), (b, c)]
    • 取出(c, d)，组成组合[(a, b), (c, d)]
  • 取出(b, c)作为第一条边。再从剩余的[(a, b), (c,d)]中取出一条边，有两种选择
    • 取出(a, b)，组成组合[(b, c), (a, b)]
    • 取出(c, d)，组成组合[(b, c), (c, d)]
  • 取出(c, d)作为第一条边。再从剩余的[(a, b), (b, c)]中取出一条边，有两种选择
    • 取出(a, b)，组成组合[(c, d), (a, b)]
    • 取出(b, c)，组成组合[(c, d), (b, c)]

代码实现

from functools import reduce from operator import add def s_tree(graph): nodes = graph[0] edges = graph[1] minEdgeNum = len(nodes) - 1 combinations = combination(edges, minEdgeNum) return [comb for comb in combinations if is_connected((nodes, comb))] def combination(l, n): if len(l) == n: return [l] if n == 1: return [[e] for e in l] elements = l.copy() return [[e] + remain for e in elements for remain in combination(l[l.index(e)+1:], n-1)] def is_connected(graph): nodes = graph[0] edges = graph[1] return len(edges) >= len(nodes) - 1 and set(nodes) == set(reduce(add, [[edge[0], edge[1]] for edge in edges], []))

functools.reduce

reduce是Python标准库提供的一个函数式的工具，其声明为：

reduce(function, iterable, initializer)

其功能是将function累积地、从左往右作用于iterable中的每一个元素。

reduce相当于如下代码：

def reduce(function, iterable, initializer=None):
    it = iter(iterable)
    if initializer is None:
        value = next(it)
    else:
        value = initializer
    for element in it:
        value = function(value, element)
    return value

is_connected

当边的数量不小于点数量减一，且边的起止点包含了所有点时，该图是连通的。

代码实现

def is_connected(graph): nodes = graph[0] edges = graph[1] return len(edges) >= len(nodes) - 1 and set(nodes) == set(reduce(add, [[edge[0], edge[1]] for edge in edges], []))

is_tree

当边的数量等于点数量减一，且边的起止点包含了所有点时，该图同时是一棵树。

代码实现

def is_tree(graph): nodes = graph[0] edges = graph[1] return len(edges) == len(nodes) - 1 and set(nodes) == set(reduce(add, [[edge[0], edge[1]] for edge in edges], []))

results matching ""

    No results matching ""