Check whether a given term represents a binary tree
Write a predicate istree/q which succeeds if and only if its argument is a Prolog term representing a binary tree. Example: ?- istree(t(a,t(b,nil,nil),nil)). Yes ?- istree(t(a,t(b,nil,nil))). No
用单元测试描述为:
from python99.btree.p401 import istree
def test_istree():
assert istree([1, [2, None, None], None]) == True
assert istree([1, [2, None], 3]) == False
根据二叉树的定义,当且当节点:
- 拥有两个子节点
- 每个子节点都是二叉树
则以该节点为根的树为二叉树。很明显,这是一个递归形式的定义。所以可以方便地使用递归方法解决。
- 给定一个节点,判断是否触及结束条件
- 对每一个子节点套用步骤1和2
- 对所有子节点返回的结果做「与」计算
结束条件有:
- 节点是空
None,空树是二叉树 - 子节点个数不等二,则以其为根的子树不是二叉树
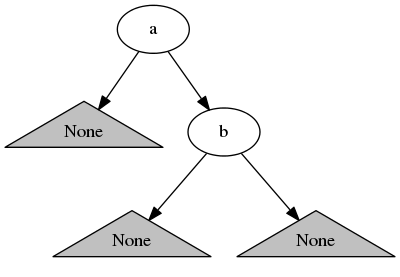
举个例子给定嵌套列表形式的树[a, [b, None, None], None]:
- 根节点是
a,其拥有两棵子树。其没有触及结束条件。继续处理子节点; - 左子节点是
b,其拥有两根子树。其没有触及结束条件。继续处理子节点; b的左子节点是None,触及了结束条件,返回值True。空树作为二叉树处理;b的右子节点是None,触及了结束条件,返回值True。空树作为二叉树处理;- 对
b的左右子节点结果作「与」计算得出结果True,再结合b自身的结果True,得出以b为根的子树是二叉树; a的右子节点是None,空树作为二叉树处理;- 对
a的左右子节点结果作「与」计算得出结果True,再结合a自身的结果True,得出以a为根的子树(即整个树)是二叉树。
代码实现:
# P401: Check whether a given term represents a binary tree
def istree(tree):
SIZE_SELF_CHILDREN = 3
if tree is None:
return True
if type(tree) is not list:
return False
if len(tree) is not SIZE_SELF_CHILDREN:
return False
if tree[0] is None:
return False
return istree(tree[1]) and istree(tree[2])