Construct minimal spanning tree

题目

Write a predicate ms_tree(Graph,Tree,Sum) to construct the minimal spanning tree of a given labelled graph. Hint: Use the algorithm of Prim. A small modification of the solution of 6.04 does the trick. The data of the example graph to the right can be found in the file p6_05.dat.

最小生成树

最小生成树是一副连通加权无向图中一棵权值最小的生成树。

在一给定的无向图 G = (V, E) 中，(u, v) 代表连接顶点 u 与顶点 v 的边（即 $(u,v)\in E）$，而 w(u, v) 代表此边的权重，若存在 T 为 E 的子集（即 $T\subseteq E）$ 且 (V, T) 为树，使得

$$w(T) = \sum_{(u,v)\subseteq T}^{} w(u,v)$$

的 w(T) 最小，则此 T 为 G 的最小生成树。

最小生成树其实是最小权重生成树的简称。

一个连通图可能有多个生成树。当图中的边具有权值时，总会有一个生成树的边的权值之和小于或者等于其它生成树的边的权值之和。广义上而言，对于非连通无向图来说，它的每一连通分量同样有最小生成树，它们的并被称为最小生成森林。

存在个数

最小生成树在一些情况下可能会有多个。例如，当图的每一条边的权值都相同时，该图的所有生成树都是最小生成树。

如果图的每一条边的权值都互不相同，那么最小生成树将只有一个。这一定理同样适用于最小生成森林。

证明（图的每一条边的权值皆不相同）：

1. 假设有两个最小生成树 $A$ 和 $B$。
2. 由于 $A$ 和 $B$ 是两个不同的最小生成树，那么 $A$ 中总会有一个或者多个边并不在 $B$ 中，设这些边中权值最低的那一条边为 $e_{k}$。
3. 由于 $B$ 是一个最小生成树，由树的一些定理可知 ${\displaystyle e_{k}\cup B}$ 必然包含一个环 $C$。
4. 因为环 $C$ 中存在一条边 $e_{m}$ 它的权值比 $e_{k}$ 。
5. 因此用 $e_{k}$ 替代 $e_{m}$， $B$ 成为了一个拥有更小权值的生成树。这和 $B$ 是最小生成树相矛盾，所以不可能存在两个最小生成树。

解题思路

以下各演算法介绍中， $E$ 表示图的边数， $V$ 表示图的顶点数。　

Prim演算法

普林演算法（Prim's algorithm），图论中的一种演算法，可在加权连通图里搜索最小生成树。意即由此演算法搜索到的边子集所构成的树中，不但包括了连通图里的所有顶点，且其所有边的权值之和亦为最小。该演算法于1930年由捷克数学家沃伊捷赫·亚尔尼克发现；并在1957年由美国计算机科学家罗伯特·普林独立发现；1959年，艾兹格·迪科斯彻再次发现了该演算法。因此，在某些场合，普林演算法又被称为DJP演算法、亚尔尼克演算法或普林－亚尔尼克演算法。

从单一顶点开始，普林演算法按照以下步骤逐步扩大树中所含顶点的数目，直到遍及连通图的所有顶点。

1. 输入：一个加权连通图，其中顶点集合为V，边集合为E；
2. 初始化：$V_{new} = \{x\}$，其中x为集合V中的任一节点（起始点），$E_{new} = \{\}$；
3. 重复下列操作，直到$V_{new} = V$：
   1. 在集合E中选取权值最小的边（u, v），其中u为集合$V_{new}$ 中的元素，而v则是V中没有加入$V_{new}$的顶点（如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）；
   2. 将v加入集合$V_{new}$中，将（u, v）加入集合 $E_{new}$ 中；
4. 输出：使用集合$V_{new}$和$E_{new}$来描述所得到的最小生成树。

举个例子，给定如下加权无向图：

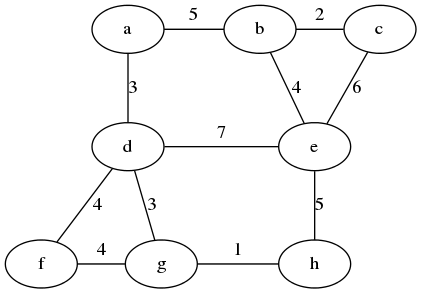
• 初始化$V_{new} = \{a\}$
• 执行下列操作，直到$V_{new} = V$：
  • 选取与$\{a\}$相邻边且另一端点不在$\{a\}$中且权重最小的$(a, d)$，将$b$加入$V_{new}$中得到$\{a, d\}$，并将$(a, d)$加入$E_{new}$中
  • 选取与$\{a, d\}$相邻且另一端点不在$\{a, d\}$中且权重最小的边$(d, g)$，将$g$加入$V_{new}$中得到$\{a, d, g\}$，并将$(d, g)$加入$E_{new}$中
  • 选取与$\{a, d, g\}$相邻且另一端点不在$\{a, d, g\}$中且权重最小的边$(g, h)$，将$h$加入$V_{new}$中得到$\{a, d, g, h\}$，并将$(g, h)$加入$E_{new}$中
  • 选取与$\{a, d, g, h\}$相邻且另一端点不在$\{a, d, g, h\}$中且权重最小的边$(d, f)$，将$f$加入$V_{new}$中得到$\{a, d, g, h, f\}$，并将$(d, f)$加入$E_{new}$中
  • ...
• 将$V_{new}$和$E_{new}$组合在一起就是一棵最小生成树

代码实现

functools.reduce

reduce是Python标准库提供的一个函数式的工具，其声明为：

reduce(function, iterable, initializer)

其功能是将function累积地、从左往右作用于iterable中的每一个元素。

reduce相当于如下代码：

def reduce(function, iterable, initializer=None):
    it = iter(iterable)
    if initializer is None:
        value = next(it)
    else:
        value = initializer
    for element in it:
        value = function(value, element)
    return value

参考

• 最小生成树
• Borůvka's algorithm
• 普林演算法
• 克鲁斯克尔演算法