Connected components
题目
Write a predicate that splits a graph into its connected components.
解题思路
对于全连通图,其只有一个连通分量。而非全连通图则有大于一个的连通分量。
从一个点开始深度遍历可以得到包含该点的连通分量。逐一以每个点为起点,对图作遍历,再把所有的遍历序列点集去重,就得到了图的所有连通分量。
举个例子,给定如下图:
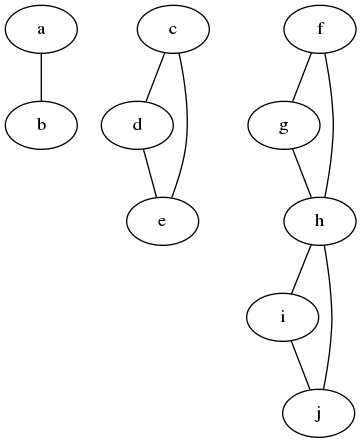
其点集为[a, b, c, d, e, f, g, h, i, j]。
- 以
a为起点深度优先遍历图得到点序列[a, b] - 以
b为起点深度优先遍历图得到点序列[b, a] - 以
c为起点深度优先遍历图得到点序列[c, d, e] - 以
d为起点深度优先遍历图得到点序列[d, e, a] - 以
e为起点深度优先遍历图得到点序列[e, c, d] - 以
f为起点深度优先遍历图得到点序列[f, g, h, i, j] - 以
g为起点深度优先遍历图得到点序列[g, h, i, j, f] - 以
h为起点深度优先遍历图得到点序列[h, i, j, f, g] - 以
i为起点深度优先遍历图得到点序列[i, j, h, f, g] - 以
j为起点深度优先遍历图得到点序列[j, h, i, f, g]
去除重复点集得到
[a, b][c, d, e][f, g, h, i, j]
然后再将边集合按上述三个点集切分。分别组合就是所求的三个连通分量。
代码实现
from python99.graph.p608 import traversal
def connected_components(g):
nodes = g[0]
connectedNodeSets = [set(traversal(g, node)) for node in nodes]
uniqueConnectedNodeSets = []
for nodeSet in connectedNodeSets:
if nodeSet not in uniqueConnectedNodeSets:
uniqueConnectedNodeSets.append(nodeSet)
return [(list(nodeSet), linkedEdges(g, list(nodeSet))) for nodeSet in uniqueConnectedNodeSets]
def linkedEdges(g, nodes):
allEdges = g[1]
edges = []
for edge in allEdges:
if edge[0] in nodes or edge[1] in nodes:
edges.append(edge)
return edges