P126: Generate the combinations of K distinct objects chosen from the N element of a list

生成从长度为N的列表中选取K个不同元素的组合。经典的组合问题。当N>K时，符合要求的组合不止一个，意味着本题的解垐返回所有符合要求的组合。

第一个难点是测试，如何判断返回的解是否正确？假如，存在一个已被证明正确的实现。针对同一个输入，我们的实现跟「已被证明正确的实现」返回相同的结果，则可以认定我们的实现是正确的。很巧，Python标准库里提供的itertools实现了组合方法itertools.combinations(iterable, r)。我们以itertools.combinations为基准，任何行为与其一致的实现都是正确的。完整的测试用例代码：

下一个难点就是实现了。题目要求罗列所有符合要求的组合，也就是在所有组合中搜索。可以使用回溯法（backtracking）。

回溯法是暴力搜索法中的一种。 对于某些计算问题而言，回溯法是一种可以找出所有（或一部份）解的一般性演算法，尤其适用于约束满足问题（在解决约束满足问题时，我们逐步构造更多的候选解，并且在确定某一部份候选解不可能补全成正确解之后于弃继续搜索这个部份候选解本身及其可以拓展出的子候选解，转而测试其他的部份候选解）。^{wiki-backtracking}

换言之，回溯法是在构造包含所有满足问题约束的解的树。每一个满足约束的解都由多个部份组成，而每一部份的取值都会影响其后部份。根到叶子节之间的路径即是一个可行解。所有路径的集合即是所有可行解的集合。

举个例子，给定列表[a, b, c, d,]，求从中抽取3个不相同元素，求所有的3个元素组合。

1. 第一层有四个选择a, b, c, d
2. 当第一层选了a第二层有三个选择b, c, d。当一层选b时，第二层有两个选择c, d。当第一层选c时，第二层仅有一个选择d。而当第一层选d时，第二层就没有选择余地了
3. 当第二层选了b时，第三层还有c, d两种可选。当第二层选了c时，第三曾仅余一个选项d。而当第二层选了d，则第三层则没有选项可选
4. 最后，所有从根节点到叶子节点，深度等于3的路径，即为所有满足约束的组合

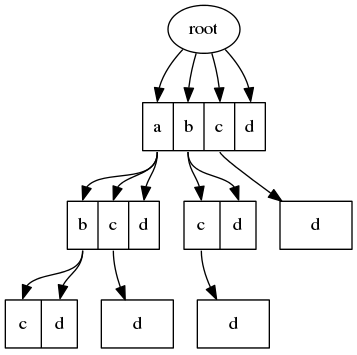
树的构造可以用递归实现。每一层都是从列表中抽取一个元素，直至剩余列表为空或深度已满足约束。因为问题求的是组合不是排列，相同元素但顺序不同的列表被认为是同一个组合。所以，剩余列表不是去除某一个元素的列表，而是「被抽取元素」之后的列表片段。

代码实现：

参考文献

^{wiki-backtracking}. https://zh.wikipedia.org/wiki/回溯法 ↩