Construct completely balanced binary trees
In a completely balanced binary tree, the following property holds for every node: The number of nodes in its left subtree and the number of nodes in its right subtree are almost equal, which means their difference is not greater than one.
Write a predicate cbal_tree/2 to construct completely balanced binary trees for a given number of nodes. The predicate should generate all solutions via backtracking. Put the letter 'x' as information into all nodes of the tree. Example: ?- cbal_tree(4,T). T = t(x, t(x, nil, nil), t(x, nil, t(x, nil, nil))) ; T = t(x, t(x, nil, nil), t(x, t(x, nil, nil), nil)) ; etc......No
用单元测试描述为:
from python99.btree.p402 import cbal_tree
def test_cbal_tree():
assert cbal_tree(4) == [
['E', ['E', ['E', None, None], None], ['E', None, None]],
['E', ['E', None, ['E', None, None]], ['E', None, None]],
['E', ['E', None, None], ['E', ['E', None, None], None]],
['E', ['E', None, None], ['E', None, ['E', None, None]]]
]
这个题目可以用分治法解。整个问题是「构造包含N个节点的完全平衡二叉树」,可以被分解为三个小问题:
- 从N个节点中取一个节点作为根节点;
- 将剩余节点平分为二,相差不超过一,分别用于构造左右子树。
第2步又可以继续分解下去,直至最小问题「N为0」。
举个例子,给定N为4,则:
- 取一个为根节点,剩余3。将3平分为2和1,枣差不超过1。分别用于构造左右子树。
- 用2个节点构造左子树。先取一个作为子树的根节点,剩余1个节点。平分1为1和0,分别用于构造左右子树。
- 用1构造左子树,取一个作为子树的根。剩余0,不分后为0和0。
- 包含0个节点的右子树只能为空树
- 包含0个节点的右子树只能为空树
- 包含0个节点的右子树只能是空树
- 用1构造左子树,取一个作为子树的根。剩余0,不分后为0和0。
- 用1个节点构造右子树﹐先取一个作为根。剩余0,平分为0和0
- 包含0个节点的左子树只能是空树
- 包含0个节点的右子树只能是空树
- 用2个节点构造左子树。先取一个作为子树的根节点,剩余1个节点。平分1为1和0,分别用于构造左右子树。
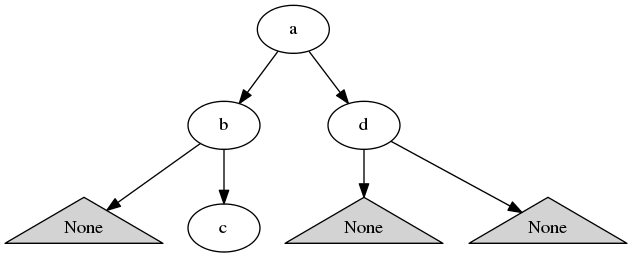
伐码实现:
import itertools
def cbal_tree(n):
if n == 0:
return [None]
element = 'E'
num_of_right = (n-1)//2
num_of_left = (n - 1) - num_of_right
a = [[element, left, right] for left in cbal_tree(num_of_left) for right in cbal_tree(num_of_right)]
b = [[element, left, right] for left in cbal_tree(num_of_right) for right in cbal_tree(num_of_left)]
result = a + b
return [ii for n,ii in enumerate(result) if ii not in result[:n]]