Knight's tour
题目
Another famous problem is this one: How can a knight jump on an NxN chessboard in such a way that it visits every square exactly once?
Hints: Represent the squares by pairs of their coordinates of the form X/Y, where both X and Y are integers between 1 and N. (Note that '/' is just a convenient functor, not division!) Define the relation jump(N,X/Y,U/V) to express the fact that a knight can jump from X/Y to U/V on a NxN chessboard. And finally, represent the solution of our problem as a list of N*N knight positions (the knight's tour).
骑士巡逻
骑士巡逻(英语:Knight's tour)是指在按照西洋棋中骑士的规定走法走遍整个棋盘的每一个方格,而且每个网格只能够经过一次。假若骑士能够从走回到最初位置,则称此巡逻为「封闭巡逻」,否则,称为「开巡逻」。对于8*8棋盘,一共有26,534,728,821,064种封闭巡逻,但是到底有多少种开巡逻仍然未知。
由骑士巡逻引申出了一个着名的数学问题 :骑士巡逻问题--找出所有的骑士巡逻路径。编写一个程式来找出骑士巡逻路径经常在电脑系的学生的练习中出现。骑士巡逻问题的变种包括各种尺寸的棋盘甚至非正方形的棋盘。
解题
最简单的演算法是枚举,生成所有的巡逻路径再判别是不访问了每一个方格且每个方格仅访问一次。但对于大棋盘(比如8x8)会慢到不能有限的时间内得到解。
回溯法用一种递进的方式解决问题。其在生成所有巡逻路径的中途就可以判别不符合要求的组合,从而减少不必要的组合生成和判别。
举个例子,骑士从(1, 1)开始巡逻。按照规则,骑士可以朝八个方向移动。去除超过棋盘范围的,剩余2个选择。这里就出现了两个分支,可能的解就有两个。
| 1 | 2 | 3 | 4 | 5 | ... | |
|---|---|---|---|---|---|---|
| 1 | K | |||||
| 2 | T1 | |||||
| 3 | T2 | |||||
| 4 | ||||||
| 5 | ||||||
| ... |
以第一个分支为例,现在骑士在位置(3, 2)。按照骑士的移动规则,再去掉超出棋盘和已访问的方格,剩余5个选择。这𥚃出现了五个分支。这一步选择会影响后续巡逻路径。
| 1 | 2 | 3 | 4 | 5 | ... | |
|---|---|---|---|---|---|---|
| 1 | X | T1 | ||||
| 2 | K | |||||
| 3 | T5 | T2 | ||||
| 4 | T4 | T3 | ||||
| 5 | ||||||
| ... |
后续的移动与上类似,每一步都以当前所处位置为起点,获取可移动过去的方格。若有多个方格可选则创造巡逻路径分支。用多路树的形式描述为:
- 每一步是树的一层
- 下一步可选的方格即是该节点的子节点
- 从叶子节点到根节点的路径即为完整的巡逻路径。若其访问了所有的方格(路径上节点数量等于方格数量),则其为一个可行解
上述头三步巡逻路径可用多路树描述为:
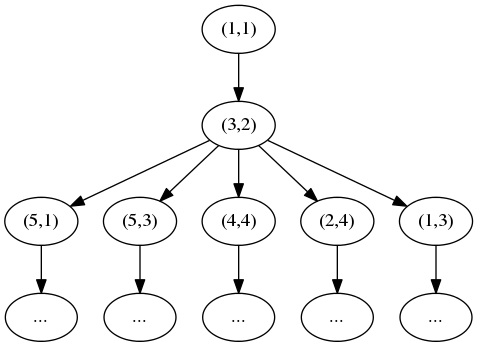
当叶子节点到根节点的路径长度等于方格縂数时,该路径即是一个可行解。当叶子节点到根节点的路径长度小于方格縂数时(没有后续可移动的方格),则该节点往下的子树都不可能是可行解,可以直接排除。