Huffman code.

First of all, consult a good book on discrete mathematics or algorithms for a detailed description of Huffman codes!

We suppose a set of symbols with their frequencies, given as a list of fr(S,F) terms. Example: [fr(a,45),fr(b,13),fr(c,16),fr(e,9),fr(f,5)]. Our objective is to construct a list hc(S,C) terms, where C is the Huffman code word for the symbol S. In our example, the result could be Hs = [hc(a,'0'),hc(b,'101'),hc(c,'100'),hc(e,'1101'),hc(f,'1100')][hc(a,'10'),...etc.]. The task shall be performed by the predicate huffman/2 defined as follows:

% huffman(Fs,Hs) :- Hs is the Huffman code table for the frequency table Fs

Huffman code

Huffman coding uses a specific method for choosing the representation for each symbol, resulting in a prefix code (sometimes called "prefix-free codes", that is, the bit string representing some particular symbol is never a prefix of the bit string representing any other symbol). Huffman coding is such a widespread method for creating prefix codes that the term "Huffman code" is widely used as a synonym for "prefix code" even when sich a code is not produced by Huffman's algorithm.

Informal description

Given A set of symbols and their weights (usually proportional to probabilities). Find A prefix-free binary code (a set of codewords) with minimum expected codeword length (equivalently, a tree with minimum weighted path length from the root).

Formalized description

Input Alphabet $A=(a_{1},a_{2},\cdots ,a_{n})$ , which is the symbol alphabet of size $n$ . Tuple $W=(w_{1},w_{2},\cdots ,w_{n})$ , which is the tuple of the (positive) symbol weights (usually proportional to probabilities), i.e. $w_{i}=\mathrm {weight} \left(a_{i}\right),1\leq i\leq n$ .

Output. Code $C\left(W\right)=(c_{1},c_{2},\cdots ,c_{n})$ , which is the tuple of (binary) codewords, where $c_{i}$ is the codeword for $a_{i},1\leq i\leq n$ .

Goal. Let $L\left(C\left(W\right)\right)=\sum _{i=1}^{n}{w_{i}\times \mathrm {length} \left(c_{i}\right)}$ be the weighted path length of code $C$ . Condition: $L\left(C\left(W\right)\right)\leq L\left(T\left(W\right)\right)$ for any code $T\left(W\right)$ .

单元测试

def test_huffman(): assert huffman([ ('a', 45), ('b', 13), ('c', 12), ('d', 16), ('e', 9), ('f', 5) ]) == [ ('a', '11'), ('b', '011'), ('c', '010'), ('d', '10'), ('e', '001'), ('f', '000') ]

解题思路

首先，将符号按权重排序。然后，构造一个二叉树，使权重小的符号处于权重大的符号的下层。最后，从树的根开始遍历，每遍历一层就在前缀一位代码。

举个例子，假设有符号a,b,c,d,e,f，其权重分别为45,13,12,16,9,5，即符号权重对列表[(a,45),(b,13),(c,12),(d,16),(e,9),(f,5)]。

首先，按权重从小到大排序，得到[(f,5),(e,9),(c,12),(b,13),(d,16),(a,45)]。

然后，构造二叉树。当使用多层嵌套的列表存储二叉树时，二叉树的构建就等于递归合併列表中相邻的两个元素为二叉树，直至仅剩一个元素即根。

先将f和e、c和b、d和a分别合併成二叉树，得到了三棵二叉树；

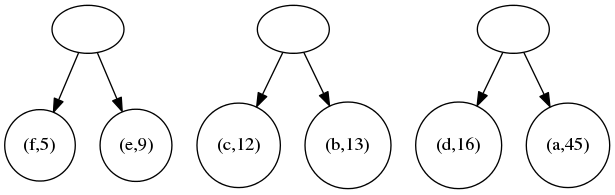
然后，将头两毎棵二叉树合併，第三棵则落单。结果得到两棵二叉树；

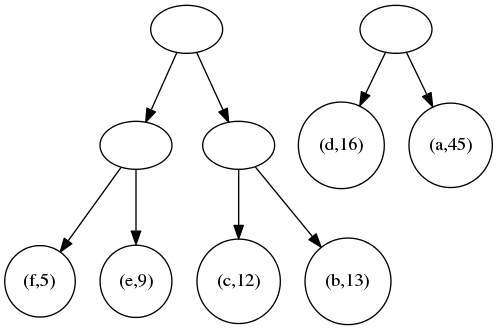
最后，将两个二叉树合併，得到最终的一棵二叉树。

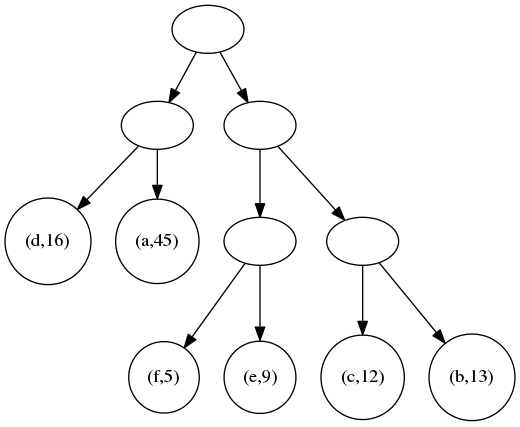
最后，后序遍历二叉树。每向下一层就加一位代码，向左子树遍历加0，向右子树遍历则加1。以(d,16)为例，从根开始到达(d,16)需：

先访问根的左子树，所以第一位代码为0
再访问左子树，代码再加一位0，为00
到达(d,16)，所以最终代码为00。

代码实现

# Huffman code def huffman(fs): sortedFs = sorted(fs,key=lambda f: f[1]) tree = constructTree(sortedFs) return sorted(traversal(tree[0]),key=lambda x:x[0]) def constructTree(sortedList): if len(sortedList) ==1: return sortedList result =[] for i in range(0, len(sortedList),2): e = sortedList[i] if i+1 >= len(sortedList): result.append(e) else: result.append([e,sortedList[i+1]]) return constructTree(result) def traversal(tree): if type(tree) is tuple: # leaf return [(tree[0],'')] leftHs = [] rightHs = [] if len(tree) > 0: # has left child leftHs = [(lambda e: (e[0],'0'+e[1]))(e) for e in traversal(tree[0])] if len(tree) > 1: # has right child rightHs = [(lambda e: (e[0],'1'+e[1]))(e) for e in traversal(tree[1])] return leftHs + rightHs

参考文献

Huffman coding

P305