二分图
题目
Write a predicate that finds out whether a given graph is bipartite.
二分图
二分图又称双分图、二部图、偶图,指顶点可以分成两个互斥的独立集和的图,也就是在任两个同在或的顶点不相邻。
二分图又称作二部图,是图论中的一种特殊模型。 设 是一个无向图,如果顶点V可分割为两个互斥的子集 ,并且图中的每条边的两个端点和分别属于这两个不同的顶点集 ,则称图为一个二分图。
无向图为二分图的充分必要条件是,至少有两个顶点,且其所有回路的长度均为偶数。
可以将和当做一个着色:中所有顶点为蓝色,中所有顶点着绿色,每条边的两个端点的颜色不同,符合图着色问题的要求。相反的,非二分图无法被二着色,例如 (3 个顶点的完全图),将其中一个顶点着蓝色并且另外一个着绿色后,第三个顶点与上述具有两个颜色的顶点相连,无法再对它着蓝色或绿色。
二分性测试
给定一个图,使用深度优先搜寻法,可以在线性时间内判断它是否为二分图,并输出一个二着色 (若答案为是),或是一个奇环 (若答案为否)。方法是先用深度优修搜寻法找出图的一个深度优先搜寻森林 (各连通部分取一个深度优先搜寻树),这是图的一个生成森林。接着运用树的搜寻将森林二着色,也就是依序各顶点着和它的父节点相异的颜色。现在检查原图中深度优先搜寻森林以外的其他边,如果所有边的两端点都不同颜色,则这也是原图的一个二着色,并且输出它;如果有一个边 e 的两端点相同颜色,则此两端点在同一个连通部分,也就是在森林的同一棵树上,找出在森林中,连接两端点的路径 P,因为 P 上的顶点的颜色是交错出现的,因此 P 有偶数个顶点,加上 e 就形成一个奇环,并且输出它。
事实上,在上述的演算法中,深度优先搜寻森林只是作为一个生成森林,让我们来着色。因此,用不同的方式获得的别的生成森林仍然可以使演算法可以运作,例如,可以用广度优先搜寻取出广度优先搜寻森林。
如果原图是线段,或其他二维空间的物件,的交集图,并且有 n 个顶点,则可以在时间内输出一个二着色或奇环,纵使它的边树可能会高达。
解题思路
使用二分性测试检测图是否为二分图。
首先,用深度优先搜索法求出图的深度优先搜寻森林。依次从图中每个点出发,对图做深度优先搜索。对结果去重复就得到深度优先搜索森林。
然后,对每棵搜索树进行二元标色。从顶点开始交替标色。
最后,判断所有边的两端点颜色是不不同。是则该图为二分图,否则不是。
举个例子,给定如下图
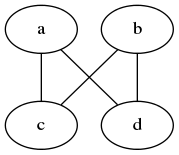
首先,使用深度优先搜索求出搜寻树[a, c, b, d]。
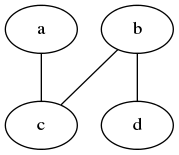
然后,对搜寻树进行二元标色。
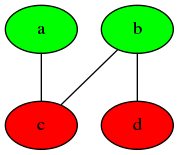
最后,检测所有边。是否存在边其两諯点颜色相同。否则该图为二分图。
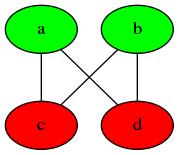
代码实现
from python99.graph.p609 import connected_components
def is_bipartite(g):
components = connected_components(g)
nodeColorDicts = [binaryColoring(component) for component in components]
allNodeColors = mergeDicts(nodeColorDicts)
for edge in g[1]:
startColor = allNodeColors[edge[0]]
endColor = allNodeColors[edge[1]]
if startColor == endColor:
return False
return True
def binaryColoring(component):
nodes = component[0]
start = nodes[0]
coloredNodes = {}
_, coloredNodes = binaryColoringTree(
component, start, True, set(), coloredNodes)
return coloredNodes
def binaryColoringTree(t, start, color, accessedNodes, coloredNodes):
coloredNodes[start] = color
accessedNodes.add(start)
linkedNodes = set(getLinkedNodes(start, t))
childNodes = linkedNodes - accessedNodes
for node in childNodes:
accessedNodes, coloredNodes = binaryColoringTree(
t, node, not color, accessedNodes, coloredNodes)
return accessedNodes, coloredNodes
def getLinkedNodes(node, graph):
edges = graph[1]
for edge in edges:
if edge[0] == node:
yield edge[1]
if edge[1] == node:
yield edge[0]
def mergeDicts(dicts):
mergedDict = {}
for dict in dicts:
for k, v in dict.items():
mergedDict[k] = v
return mergedDict



