Layout a binary tree (3)
题目

Yet another layout strategy is shown in the above illustration. The method yields a very compact layout while maintaining a certain symmetry in every node. Find out the rules and write the corresponding Prolog predicate. Hint: Consider the horizontal distance between a node and its successor nodes. How tight can you pack together two subtrees to construct the combined binary tree?
Use the same conventions as in problem 4.13 and 4.14 and test your predicate in an appropriate way. Note: This is a difficult problem. Don't give up too early!
Which layout do you like most?
单元测试描述为:
def test_layout_binary_tree():
assert layout_binary_tree(['a', ['b', None, ['d', None, None]], ['c', None, None]]) == [
('a', 2, 1),
[('b', 1, 2), None, [('d', 2, 3), None, None]],
[('c', 3, 2), None, None]
]
解题思路
X轴位置
通过计算子树每一层的「寛度」得到父子节点之的相对位置。然后再定位最左的节点,将其X轴标为1。最后再根据父子节点的相对位置标记其它节点的X轴位置。
定义二叉树中某一层的「寛度」为该层最左边和最右边节点相对于根节点的遍移量。例如,如下二叉树拥有三层,第一层根节点。第二层寛度记为(-1, 1),表示最左边的节点b在X轴上向左偏移根节点一位,最右边的节点c在X轴上偏移根节点一位。
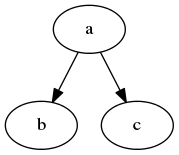
每一层节点的偏移量会下层节点的影响。想像在合併两棵子树并让它们呆得足够紧凑。在X轴上,左右两棵子树的根节点之间的空间应刚好容纳左子树中向右偏移的节点和右子树中向左偏移的节点。将左子树中右偏移量加上右子树中对应层左偏移量,即得到这个刚容纳整棵左右子树的空间。
举个例子,有如下两个二叉树:

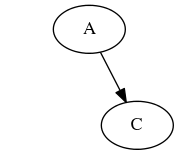
第一棵根节点以下第一层的宽度是(-1,1)。第二棵根节点以下第一层的寛度是(0,1)。所以,为了容纳两棵子树的所有节点,两棵子树根节点之间的距离至才是1+0=1,但左右子节点距合併后的新根节点要相等(X轴上),所以之间的最小距离要向上取偶,为2。
代码实现:
def countour(t):
if t[1] is None and t[2] is None:
return [(t[0], []), None, None]
if t[1] is None:
left = None
leftCountours = []
else:
left = countour(t[1])
leftCountours = left[0][1]
if t[2] is None:
right = None
rightCountours = []
else:
right = countour(t[2])
rightCountours = right[0][1]
distance = maxDistance(leftCountours, rightCountours)
print(t[0], distance)
leftShift = 0-ceil(distance/2)
if left is None:
leftShift = 0
rightShift = ceil(distance/2)
if right is None:
rightShift = 0
selfCountours = [(leftShift, rightShift)]+remainCountours(leftShift,
rightShift, leftCountours, rightCountours)
return [(t[0], selfCountours), left, right]
def maxDistance(leftCountours, rightCountours):
maxDist = 1
for i in range(0, max(len(leftCountours), len(rightCountours))):
left = 0
right = 0
if i < len(leftCountours):
left = leftCountours[i][1]
if i < len(rightCountours):
right = rightCountours[i][0]
distance = left + 1-right
if distance > maxDist:
maxDist = distance
return maxDist
def remainCountours(leftShift, rightShift, leftCountours, rightCountours):
countours = []
for i in range(0, max(len(leftCountours), len(rightCountours))):
left = 0
right = 0
if i < len(leftCountours):
left = leftCountours[i][0]
if i < len(rightCountours):
right = rightCountours[i][1]
countours.append((left+leftShift, right+rightShift))
return countours
得到每一层「寛度」即等到了父子节点之间的相对位置了(X轴)。
接着遍历再有「寛度」信息的二叉树。先定位到最左边的节点,将其X轴位置记为1。再根据相对位置计算其它节点的X轴位置。
举个例子,已得到包含每层「寛度」的二叉树
[
('a', [(-1, 1), (-1, 1)]),
[('b', [(0, 1)]), None, [('d', []), None, None]],
[('c', []), None, None]
]
- 从根节点开始大子树优先遍
- 一直探索左子节点直至最左边的节点,将其X轴位置标为1
- 以左子节点的X轴位置为基础,加上往下第一层「寛度」的左偏移量即为父节点的X轴位置
- 右子节点的X轴位置等于父节点的位置加上该层「寛度」的右偏移量
- 左子节点(非最左边节点)的位置等于父节点的位置减去该层「寛度」的左偏移量
代码实现:
def markX(t, p):
if t is None:
return None, p
if t[1] is None and p == 0:
# found the mostleft node
e = (t[0][0], 1)
p = 1
left = None
else:
left, p = markX(t[1], p)
firstLeftShift = 0
firstRightShift = 0
if len(t[0][1]) > 0:
firstLeftShift = t[0][1][0][0]
firstRightShift = t[0][1][0][1]
selfX = p-firstLeftShift
e = (t[0][0], selfX)
if t[2] is not None:
rightX = selfX+firstRightShift
right, p = markX(t[2], rightX)
else:
right = None
return [e, left, right], selfX
Y轴位置
Y轴位置的计算比较简单,Y轴的值等于节点在整棵树中所处的深度(或称为高度,根节点高度记为1,根节点往下一层高度为2,以此类推)。
使用递归方法,从根节点开始遍历。先访问自身节点再访问左右子树。访问左右子树时高度加1。根节点的高度为1,所以高度初始值1。
代码实现:
def markY(t, h):
if t is None:
return None
return [(t[0][0], t[0][1], h), markY(t[1], h+1), markY(t[2], h+1)]



