Conversions

题目

Write predicates to convert between the different graph representations. With these predicates, all representations are equivalent; i.e. for the following problems you can always freely pick the most convenient form. The reason this problem is rated (*) is not because it's particularly difficult, but because it's a lot of work to deal with all the special cases.

解

为了简单起见，我们只考虑无标无向图在四种表现形式之间的转换。

四种表现形式之间两两转换，縂共有12种用例。如果先把其它形式转换成图项形式，再从图项形式转换为目标形式，则用例就缩减为6种：

1. 边（弧）条文形式转换为图项形式
2. 相邻列表形式转换为图项形式
3. 人类友好形式转换为图项形式
4. 图项形式转换为边「弧）条文形式
5. 图项形式转换为相邻列表形式
6. 图项形式转换为人类友好形式

边（弧）条文形式转换为图项形式

边（弧）条文形式和图项形式都包含了边列表，图项形式显示地列出了节点列表。所以，从边（弧）条文形式转换到图项形式只而从边列表中析出节点列表即可。

举个例子，给定边条文形式图[(b,c), (b, f), (c, f), (f, k), (g, h)]。

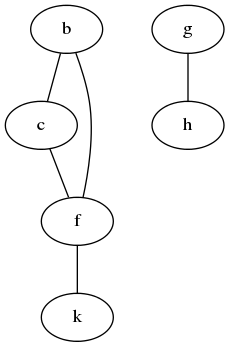
先从中析出节点列表[b, c, b, f, c, f, f, k, g, h]，再去除重复点得到点列表[b, c, f, k, g, h]，再加上边列表就得到了图项形式([b, c, f, k, g, h], (b,c), (b, f), (c, f), (f, k), (g, h)])。

代码实现：

functools.reduce

reduce是Python标准库提供的一个函数式的工具，其声明为：

reduce(function, iterable, initializer)

其功能是将function累积地、从左往右作用于iterable中的每一个元素。

reduce相当于如下代码：

def reduce(function, iterable, initializer=None):
    it = iter(iterable)
    if initializer is None:
        value = next(it)
    else:
        value = initializer
    for element in it:
        value = function(value, element)
    return value

相邻列表形式转换为图项形式

相邻列表形式将边按节点分组。在无向图中，边是无方向的。所以每一条边都有两种表示法。比如a至b之间的边，可以表示为(a, [b])和(b, [a])。用相郼列表形式表示无向图时，这两种表示法都会出现。而在图项形式中，只会包含其中一种。所以，从相列表形式转换至图项形式时要去除重复。

举个例子，给定相邻列表形式图[(b, [c, f]), (c, [b, f]), (d, []), (f, [b, c, k]), (g, [h]), (h, [g]), (k, [f])]。

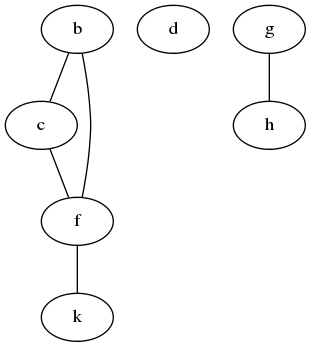
先从中析出节点列表[b, c, d, f, g, h, k]。 再从中析出边列表[(b, c), (b, f), (c, b), (c, f), (f, b), (f, c), (f, k), (g, h), (h, g), (k, f)]，去除重复后得到[(b, c), (b, f), (c, f), (f, k), (g, h)]。将节点列表和边列表合起来即是图项形式([b, c, f, d, k, g, h], [(b, c), (b, f), (c, f), (f, k), (g, h)])。

代码实现：

Lambda 表达式

小型慝名函数可以用lambda关键词来创建。lambda a, b: a+b这个函数返回两个参数的和。Lambda函数可以在任何需要函数对象的地方使用。它们在语法上限于单个表达式。从语义上讲，它们只是包裹在常规函数定义外面的语法糖。与嵌套函数定义类似，lambda函数可以引用同范围内的变量。

>>> def make_incrementor(n):
...     return lambda x: x + n
...
>>> f = make_incrementor(42)
>>> f(0)
42
>>> f(1)
43

上述例子使用lambda表达式返回一个函数。另一个用法是传入一个小函数作为参数：

>>> pairs = [(1, 'one'), (2, 'two'), (3, 'three'), (4, 'four')]
>>> pairs.sort(key=lambda pair: pair[1])
>>> pairs
[(4, 'four'), (1, 'one'), (3, 'three'), (2, 'two')]

人类友好形式转换为图项形式

以Python元组表示的人类友好形式跟边条文形式一样。

图项形式转换为边「弧）条文形式

图项形式包含了点列表和边列表，而边条文形式只有边列表。所以，将图项形式的边列表取出即为边条文形式了。

举个例子，给定图项形式图([b, c, f, d, k, g, h], [(b, c), (b, f), (c, f), (f, k), (g, h)])

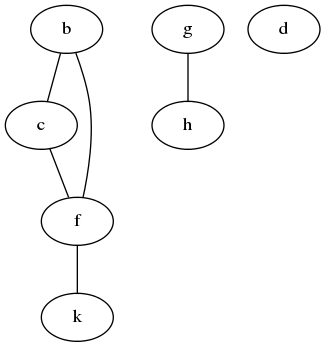
取边列表即为边条文形式[(b, c), (b, f), (c, f), (f, k), (g, h)]。

代码实现：

图项形式转换为相邻列表形式

相邻列表形式是按点分组，再找到与点相邻的其它点集合，最后关点与相邻点集合。

从图项形式转换为相邻列表形式，先取出点集合，再解出每一个点相邻点集合，最后再将其关联起来。

举个例子，给定图项形式图([b, c, f, d, k, g, h], [(b, c), (b, f), (c, f), (f, k), (g, h)])

先取出点列表[b, c, f, d, k, g, h]，再寻找每个点相邻的点。

• b相邻的点有c, f
• c相邻的点有b, f
• f相邻的点有b, c, k
• d没有相邻的点
• k相邻的点有f
• g相邻的点有h
• h相邻的点有g

代码实现：

图项形式转换为人类友好形式

以Python元组表示的人类友好形式跟边条文形式一样。