P611: Generate K-regular simple graphs with N nodes
题目
In a K-regular graph all nodes have a degree of K; i.e. the number of edges incident in each node is K. How many (non-isomorphic!) 3-regular graphs wit h 6 nodes are there?
正则图
正则图是每个顶点都有相同数目的邻居的图,即每个顶点的度相同。若每个顶点的度均为,称为-正则图。
0-正则图是没有边的图。1-正则图由不相连的边组成。2-正则图由不相连的圈组成。3-正则图称为三次图。阶为的-正则图是完全图。
在强正则图,每对相邻顶点都有相同数目 l 的共同邻居,每对非相邻顶点也有相同数目 m 节共同邻居。最小的正则而非强正则的图是6个顶点的环状图或圈。
| 0-正则图 | 1-正则图 | 2-正则图 | 3-正则图 |
|---|---|---|---|
 |
 |
 |
 |
性质
- 对于每个图及每个不小于的最大度整数 ,存在一个有作子图的-正则图。
- 若有阶为的-正则图,k是偶数或n是偶数。
解题思路
首先,使用回溯法列出N个点之间可能的所有边。然后,从所有边的集合中抽出固定条数的边和N个点组成图。包含N个点的K-正则图所包含的边条数是确定的,为。最后,再逐一检测图是否为K-正则图。
举个例子,一个包含4个点的图最多有6条边。求其2-正则图。
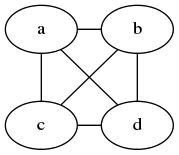
包含4个点的2-正则图一定由4条边组成()。从6条边中抽取4条边有多种组合方式。如:
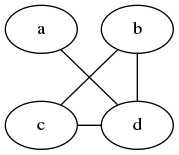
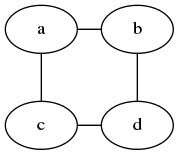
最后,逐一检测每个4条边组合构成的图。如果其每个点的度都是2,则其为2-正则图。
代码实现
from python99.graph.p607 import degree
def gen_regular(k, n):
if k*n % 2 != 0:
return []
nodes = [e for e in range(1, n+1)]
allEdges = genEdges(nodes)
edgeCombinations = combination(allEdges, k*n/2)
return [(nodes, edges) for edges in edgeCombinations if isRegular((nodes, edges), k)]
def genEdges(nodes):
if len(nodes) == 2:
return [(nodes[0], nodes[1])]
head = nodes[0]
remain = nodes[1:]
edges = [(head, end) for end in remain]
return edges + genEdges(remain)
def combination(l, n):
if len(l) == n:
return [l]
if n == 1:
return [[e] for e in l]
if n == 0:
return []
return [[head] + remain for head in l for remain in combination(l[l.index(head)+1:], n-1)]
def isRegular(g, k):
nodes = g[0]
for node in nodes:
if degree(g, node) != k:
return False
return True
How many (non-isomorphic!) 3-regular graphs with 6 nodes are there?
直接计算所有的正则图再合计数量。
from python99.graph.p611 import gen_regular
def test_gen_regular():
assert gen_regular(2, 3) == [
([1, 2, 3], [(1, 2), (1, 3), (2, 3)])
]
assert gen_regular(2, 4) == [
([1, 2, 3, 4], [(1, 2), (1, 3), (2, 4), (3, 4)]),
([1, 2, 3, 4], [(1, 2), (1, 4), (2, 3), (3, 4)]),
([1, 2, 3, 4], [(1, 3), (1, 4), (2, 3), (2, 4)])
]
assert len(gen_regular(3, 6)) == 70