Von Koch's conjecture
题目
Several years ago I met a mathematician who was intrigued by a problem for which he didn't know a solution. His name was Von Koch, and I don't know whether the problem has been solved since.
Anyway, the puzzle goes like this: Given a tree with N nodes (and hence N-1 edges). Find a way to enumerate the nodes from 1 to N and, accordingly, the edges from 1 to N-1 in such a way, that for each edge K the difference of its node numbers equals to K. The conjecture is that this is always possible.
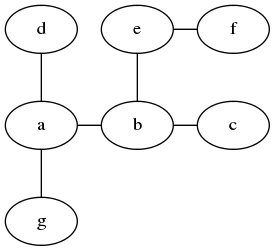
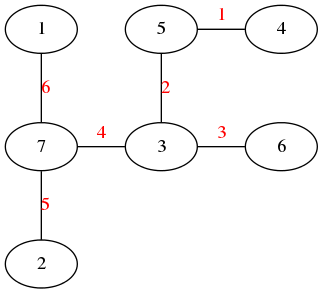
For small trees the problem is easy to solve by hand. However, for larger trees, and 14 is already very large, it is extremely difficult to find a solution. And remember, we don't know for sure whether there is always a solution!
解题
树可以用图的图项形表示。
使用回溯法列出所有的点和边序号组合,再根据规则:
- 所有点的序号都是1至N的整数,且不重复
- 所有边的序号都是1至N-1的整数,且不重复
- 边的序号等于两端点序号的差值
选出符合要求的组合即为解。根据已知条件,边的序号由两端点序号决定。所以,实际上只需要列出点序号组合即可。当所有点的序号确定,边的序号也都确定了。
在回溯的过程中可以提前排除不符合要求的组合,而不需要列出完整的组合再排除。这样可以大大减少不必要的计算。
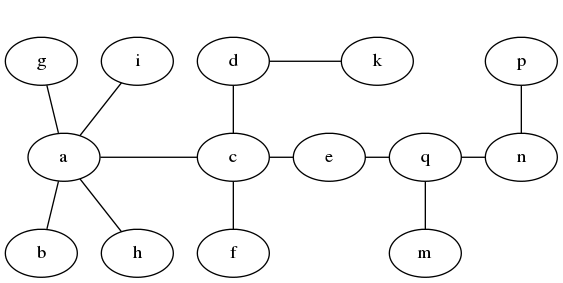
如下图,从b开始给点分配序号。当分到c时,边的序号就出现了重复。此时就无需再罗列d和e的序号组合了。因为无论d和e序号如何,整个组合都不会是符合条件的解。
代码实现
from python99.graph.p608 import traversal
def conjecture(g):
nodes = g[0]
edges = g[1]
markedNodes = []
remainNos = [no for no in range(1, len(nodes)+1)]
markedNodes = doConjecture(nodes, edges, markedNodes, remainNos)
return [markEdge((nodesWithNo, edges)) for nodesWithNo in markedNodes]
def doConjecture(nodes, edges, markedNodes, remainNos):
if len(nodes) == 0:
return [[]]
v = nodes[0]
remainNodes = nodes[1:]
return [[(v,no)]+remain
for no in remainNos
for remain in doConjecture(remainNodes, edges, markedNodes + [(v, no)], [remainNo for remainNo in remainNos if remainNo != no])
if isValid(markedNodes+[(v, no)], edges)]
def isValid(markedNodes, edges):
maxEdgeNo = len(edges)
minEdgeNo = 1
usedEdgeNos = set()
nodeNoDict = {}
for markedNode in markedNodes:
nodeNoDict[markedNode[0]] = markedNode[1]
for edge in edges:
start = edge[0]
end = edge[1]
if start in nodeNoDict and end in nodeNoDict:
diff = abs(nodeNoDict[start]-nodeNoDict[end])
if diff < minEdgeNo or diff > maxEdgeNo:
return False
elif diff in usedEdgeNos:
return False
else:
usedEdgeNos.add(diff)
return True
def markEdge(g):
nodeNoDict = {}
for markedNode in g[0]:
nodeNoDict[markedNode[0]] = markedNode[1]
edges = g[1]
markedEdges = []
for edge in edges:
start = edge[0]
end = edge[1]
diff = abs(nodeNoDict[start]-nodeNoDict[end])
markedEdges.append((start,end,diff))
return (g[0],markedEdges)
参考



