P113: Run-length encoding of a list (direct solution)

游程编码（直接方案）。在P111中已经实现一个游程编码，但那个实现重用了很多之前实现的方法。本题是要从零开始实现一遍游程编码。 还是先写测试用例用来验证实现：

这个问题可以分两步解决，先把列表编码为由[N, E]项组的列表（E表示连续重复元素的值，N表续重复元素重复的次数），再将N为1的[N, E]项简化为E。

第一步可以用递归解决。递归的通用模式是：

1. 将一个大问题拆分为一个极简单的小问题和一个较小的问题，较小的问题可以被继续拆分直至剩余一个极简单问题或空
2. 然后逐个解决极简单的小问题
3. 最后将所有极简单小问题的解归併起来

本例中，「一个大问题」是用游程编码编码一个列表，其可以被拆分为「一个极简单的小问题-编码头元素」和「一个较小的问题-编码剩余列表」，剩余列表可以被继续拆分直至为空。然后解决「极简单问题」编码单个元素。最后归併结果。归併结果有点复杂，要分三种情况：

1. 编码后的剩余列表为空，直接拼接头元素和空列表
2. 编码后的剩余列表不为空且第一个[N, E]项中的E和拆分出来的头元素相同，则合併头元素进第一个[N, E]项
3. 编码后的剩余列表不为空且第一个[N, E]项中的E和拆分出来的头元素不相同，则为头元素构造一个[N, E]项，拼接编码后的剩余列表

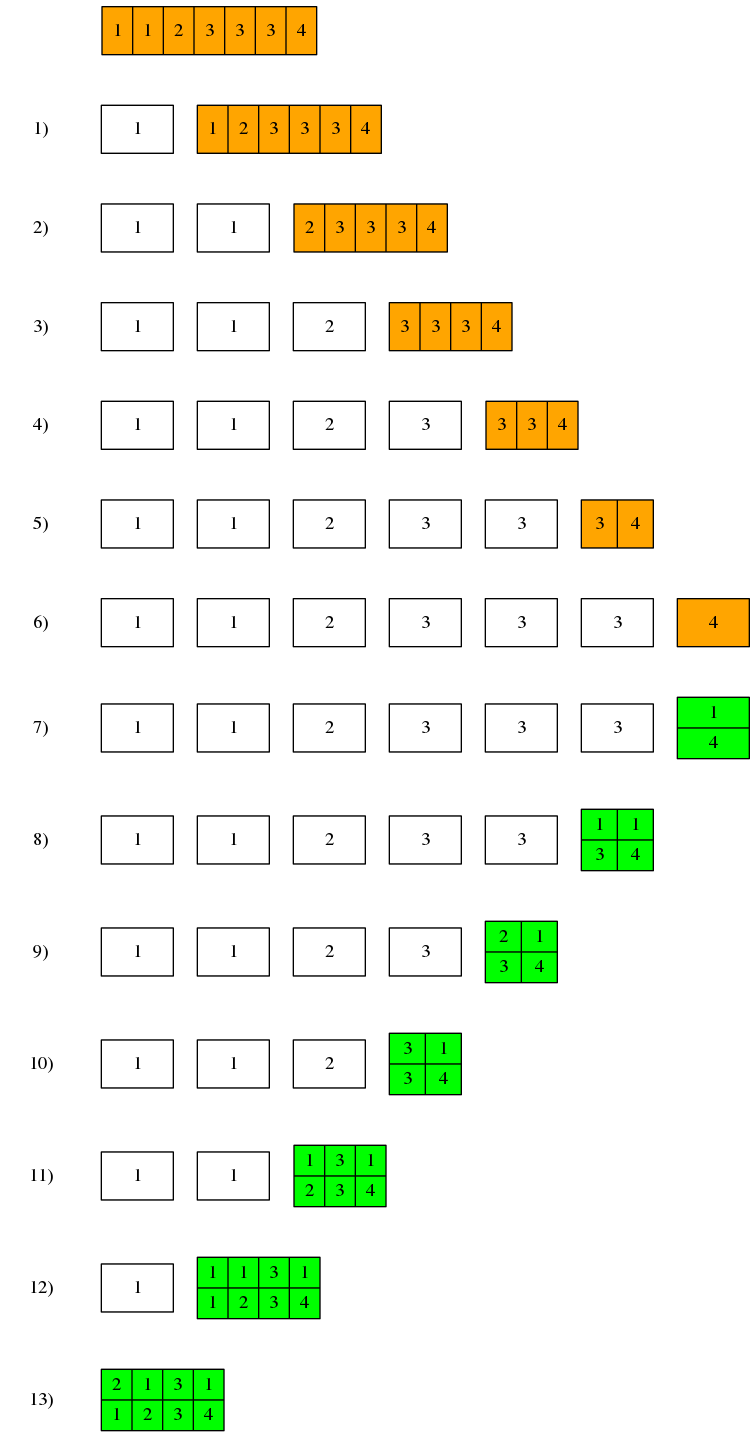
举个例子，给定列表[1, 1, 2, 3, 3, 3, 4]：

1. 将列表[1, 1, 2, 3, 3, 3, 4]拆分为元素1和剩余列表[1, 2, 3, 3, 3, 4]
2. 将列表[1, 2, 3, 3, 3, 4]继续拆分为元素1和剩余列表[2, 3, 3, 3, 4]
3. 将列表[2, 3, 3, 3, 4]继续拆分为元素2和剩余列表[3, 3, 3, 4]
4. 将列表[3, 3, 3, 4]继续拆分为元素3和剩余列表[3, 3, 4]
5. 将列表[3, 3, 4]继续拆分为元素3和剩余列表[3, 4]
6. 将列表[3, 4]继续拆分为元素3和剩余列表[4]
7. [4]中仅含有一个元素，将其编码为[[1, 4]]
8. 这一层中拆分出来的头元素3与编码后剩余列表中第一个元素，即[N, E]项中的E 4不相同，所以将头元素3编为单独的[N, E]项[1, 3]，并和编码后的剩余列表拼接在一起，得到[[1, 3], [1, 4]]
9. 这一层拆分出来的头元素3与编码后剩余列表中第一个元素的E 3相同，所以把头元素併入第一个元素中，得到[[2, 3], [1, 4]]
10. 这一层中拆分出来的头元素3与编码后剩余列表中第一个元素[2, 3]中的E相同，所以把头元素併入第一个元素中，得到[[3, 3], [1, 4]]
11. 这一层中拆分出来的头元素2与编码后剩余列表中第一个元素[3, 3]中的E不相同，所以把头元素编为单独的[1, 2]，并和编码后的剩余列表拼接在一起，得到[[1, 2], [3, 3], [1, 4]]
12. 这一层中拆分出来的头元素1与编码后剩余列表中第一个元素[1, 2]中的E不相同，所以把头元素编为单独的[1, 1]，并和编码后的剩余列表拼接在一起，得到[[1, 1], [1, 2], [3, 3], [1, 4]]
13. 最初一层中拆分出来的头元素1与编码后剩余列表中第一个元素[1, 1]中的E相同，所以把头元素併入第一个元素中，得到最终结果[[2, 1], [1, 2], [3, 3], [1, 4]]

第二步就对列表逐元素转换，如果N为1则转换为E，否则保持不变。使用Python内建的List comprehension可以简洁地实现列表逐元素转换。List comprehension的形式为：

[f(x) for x in l]

本例中，f是一个分段函数（piecewise function）：

$$f([N, E]) = \begin{cases} E & \text{if N=1} \\ (N, E) & \text{otherwise} \end{cases}$$

完整的代码实现：