P302: Truth tables for logical expression
延用P301中定义的逻辑运算符。这次逻辑表达式以更自然的方式描述,比如:A and (A or not B)。运算符之间的人优先级按照常规优先级,() > not > and == or == nand == nor == xor == impl > equ。
至下而上的解决方法为:
- 解析运算符后置表达式
- 将运算符中置表达式转换为运算法后置表达式
- 将字符串形式的表达式分解列表形式,即将字符串拆解为离散的运算符和运算数
解析运算符后置表达式
按照运算符所处的位置,表达式可分为:
- 运算符前置表达式,例如
and A or A not B
- 运算符中置表达式,例如
A and (A or not B)
- 运算符后置表达式,例如
B not A or A and
其中,运算符前置表达式和运算符后置表达式中无需也不能使用括号()改变优先级,运算符在表达式中的顺序即为其作用顺序。运算符前置表达式和运算符后置表达式解析较运算符中置表达式更简单。
任意表达式都是由「运算符(operator)」和「操作数(operand)」组成,其内部结构可以「树(tree)」来表示。其中:
- 根节点一定是运算符
- 叶子节点一定是操作数
- 运算符节点拥有相应数量的子节点,一元运算符拥有一个子节点,二元运算符拥有两个子节点,依此类推
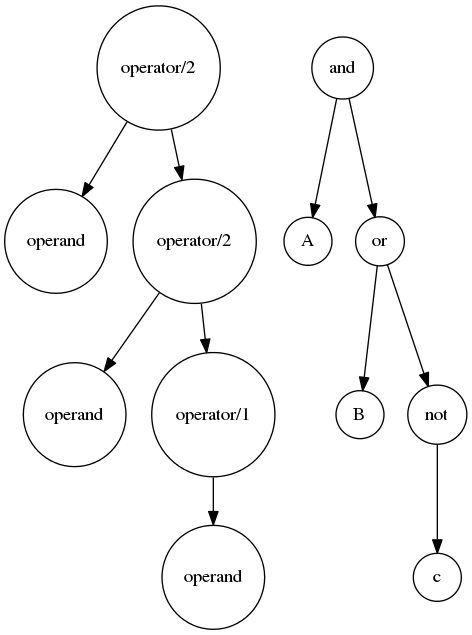
运算符后置表达式其实就是「深度优先后序遍历(depth first post-order traversal)」表达式结构树。
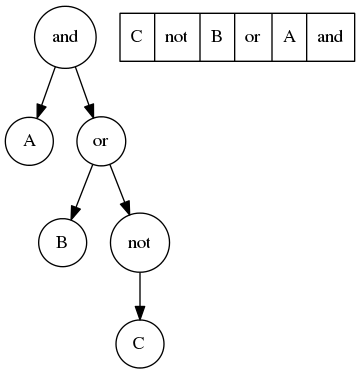
计算运算符后置的表达式规则很简单:
- 从左往右逐一处理表达式中的每一个元素
- 若元素是操作数则压一个「栈(stack)」
- 若元素是运算符则从栈中弹出相应数量的操作数,一元运算符则弹出一个操作数,二元运算符则弹出两个操作数,依此类推。然后在操作数上执行运算符对应的运算,并把结果压入栈中
- 直到到达表达式末尾,栈顶元素即为表达式的值
举个例子,已知一个以列表形式表示的运算符后置表达式[False, 'not', True, 'or', False, 'and'],逐个处理元素:
- 第一个元素
False是操作数,压入操作数栈
not是一元运算符,从栈中弹出一个操作数,执行非运算- 将结果
True压入栈
True是操作数,压入栈or是二元运算符,从栈中弹出两个操作数并执行或运算- 将结果
True压入栈
False是操作数,压入栈and是二元运算符,从栈中弹出两个操作数并执行与运算- 将结果
False压入栈。此时已至表达式末尾,栈顶元素False即为原表达式的值
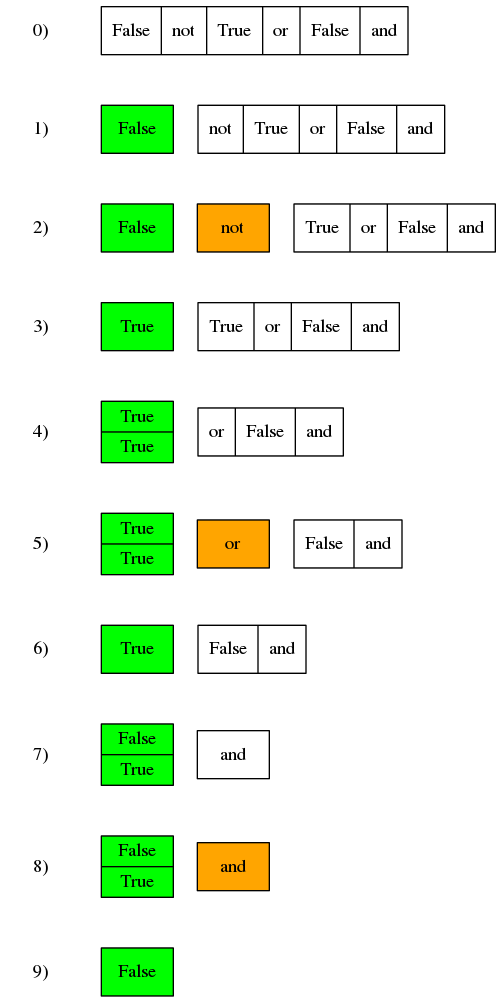
代码实现
def evaluate(exprInList):
stack = []
operatorBuilder = OperatorBuilder()
for e in exprInList:
if type(e) == bool:
stack.append(e)
else:
op = operatorBuilder.buildFor(e)
if op.isUnary():
a = stack.pop()
stack.append(op.apply(a))
elif op.isBinary():
a = stack.pop()
b = stack.pop()
stack.append(op.apply(a, b))
else:
raise "Unsupported operator " + e
return stack.pop()
先使用列表构造操作数栈,然后逐一处理以列表形式展现的表达式中的元素。当元素是bool型时则为操作数,压入栈;否则即为运算符,这里使用构造器模式构造相应的Operator对象并执行计算,再把计算结果压入栈中。
运算符类和构造器类见以下代码:
class Operator:
def __init__(self, symbol):
self.symbol = symbol
def isUnary(self):
return False
def isBinary(self):
return False
def apply(self, a, b=None):
raise NotImplementedError
class Not(Operator):
def __init__(self):
super().__init__('not')
def isUnary(self):
return True
def apply(self, a):
return not a
class And(Operator):
def __init__(self):
super().__init__('and')
def isBinary(self):
return True
def apply(self, a, b):
return a and b
class Or(Operator):
def __init__(self):
super().__init__('or')
def isBinary(self):
return True
def apply(self, a, b):
return a or b
class Nand(Operator):
def __init__(self):
super().__init__('nand')
def isBinary(self):
return True
def apply(self, a, b):
return not (a and b)
class Nor(Operator):
def __init__(self):
super().__init__('nor')
def isBinary(self):
return True
def apply(self, a, b):
return not (a or b)
class Xor(Operator):
def __init__(self):
super().__init__('xor')
def isBinary(self):
return True
def apply(self, a, b):
return a != b
class Impl(Operator):
def __init__(self):
super().__init__('impl')
def isBinary(self):
return True
def apply(self, a, b):
return (not a) or b
class Equ(Operator):
def __init__(self):
super().__init__('equ')
def isBinary(self):
return True
def apply(self, a, b):
return a == b
class Nop(Operator):
def __init__(self):
super().__init__('op')
class OperatorBuilder:
def __init__(self):
self._operatorDefinition = {
Not().symbol: Not(),
And().symbol: And(),
Or().symbol: Or(),
Nand().symbol: Nand(),
Nor().symbol: Nor(),
Xor().symbol: Xor(),
Impl().symbol: Impl(),
Equ().symbol: Equ()
}
def buildFor(self, symbol):
if symbol in self._operatorDefinition:
return self._operatorDefinition[symbol]
else:
return Nop()
单元测试
def test_evaluate():
assert evaluate([True, 'not']) == False
assert evaluate([False, 'not', True, 'or', False, 'and']) == False
assert evaluate([False, False, True, 'not', 'or', 'and']) == False
运算符中置表达式转运算符后置表达式
先将运算符中置表达式转换为树状结构,再以「深度优先后序遍历(depth first post-order traversal)」生成运算符后置表达式。
运算符优先级是运算符中置表达式最大的不同点。在运算符前置和后置表达式中,运算符出现的位置与执行的顺序相同。运算符中置表达式则不然。在运算符中置表达式中,运算符具有不同的优先级,高优先级运算符先于低优先级运算符执行,相同优先级的运算符才按出现的位置从左往右执行。且运算符中置表达式引入了括号「()」用以强置改变优先级。被括号包裹的表达式片断拥有最高的优先级。
将操作数也视为一种运算符的话,其拥有最高的优先级。
operand > () > not > and == nand == nor == xor == impl > or == equ
假设,已将文本格式的运算符表达式解析成列表形式,其中每一个元素是操作数或运算符。构造表达式结构树的步骤为:
- 逐一读取列表中的元素,构成对应类型的节点。维持一个到树中最后操作节点的引用,初始为引用根节点
- 若最后操作节点为空即树为空,则将新节点插入为根节点
- 若最后操作节点不为空且新节点优先级大于最后操作节点,则将新节点插入为最后操作节点的子节点,并将最后操作节点引用指向新节点
- 若最后操作节点不为空且新节点优先级不大于最后操作节点,则向上寻找第一个优先级小于新节点的节点,将新节点作为其子节点插入。若不能向上找到优先级小于新节点的节点,则将新节点插入为根节点。向上寻找低优先级节点不能越过括号节点。括号在运算符中置表达式中是用于改变优先级的,被括号包裹的表达式片断拥有最高的优先级。而在结构树中,越深的子节点拥有越高的优先级。所以,在向上寻找低优先级节点时不能越过括号节点。最后操作节点引用指向新节点。
- 若新节点为右括号则向上寻找最近的左括号节点,并将其消除掉。
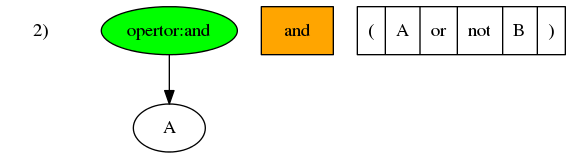
举个例子,假设一个运算符中置表达式以列表形式表示为['A', 'and', '(', 'A', 'or', 'not', 'B', ')']。从左往右逐一处理列表中的元素:
- 第一个元素
A是操作数,且树是空的,所以将A插入为根节点。
- 第二个元素
and是运算符,所有运算符的优先级都小于操作数。所以从最后操作节点A向上寻找优先级小于and的节点。节点A已经是根节点,所以将and插入为A的父节点即根节点。
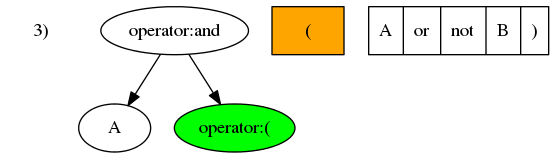
- 第三个元素
(优先级大于最后操作节点and,所以将其插入为and的子节点。
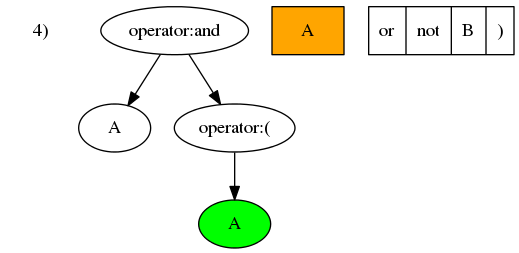
- 第四个元素
A是操作数,操作数的优先级大于所有运算符,包括(),所以将其插入为(的子节点。
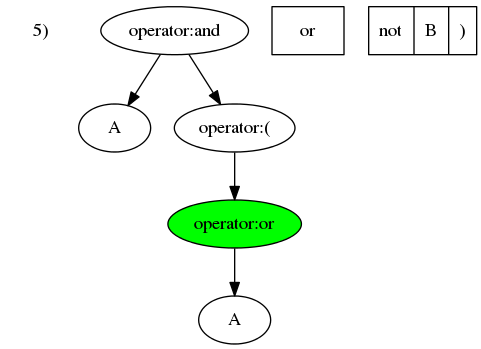
- 第五个元素
or是运算符,优先级小于最后操作节点A。所以向上寻找优先级小于or的节点。但是,在向上搜寻的过程中,遇到了(。在运算符中置表达式中,括号是用以改变优先级的。向上搜索应止于括号。所以,or应被插入至(和A之间。
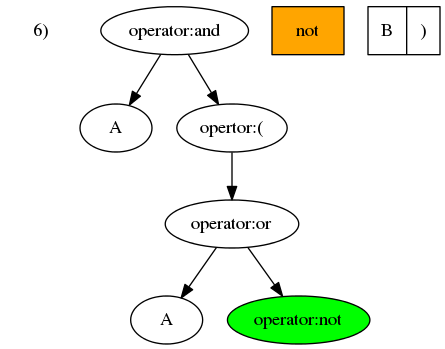
- 第六个元素
not是运算符,且其优先级大于最后操作节点or。所以应将其插入为or的子节点。
- 第七个元素
B操作数,操作数的优先级大于所有运算符。所以其应被插入为最后操作节点not的子节点。
- 最后一个元素是
),应向上搜寻第近的左括号)并将其消除掉。

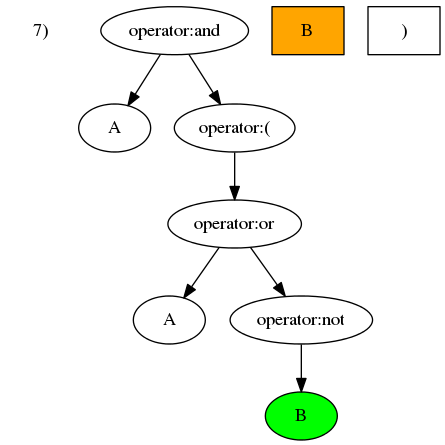
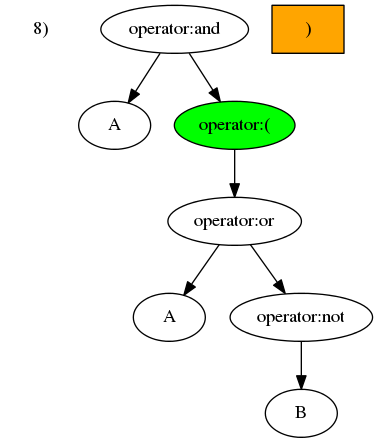
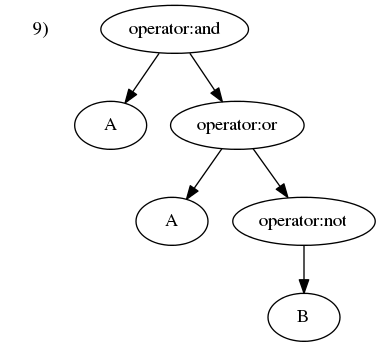
然后「后序遍历」结构树。后序遍历二叉树很简单。二叉树是一个递归结构,很以二叉树的遍历也是递归算法。
- 如果左子树不为空,则遍历左子树
- 若右子树不为空,则遍历右子树
- 访问节点值
举个例子,有如下二叉树形式的表达式:
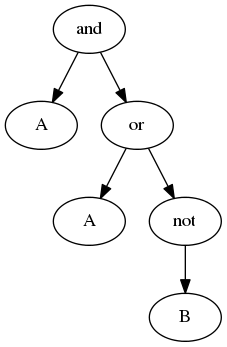
and有左子树,先遍历其左子树A没左子树,也没有右子树,访问节点值Aand的左子树遍历完毕,再遍历其右子树and的右子树拥有左右两个子树or的左子树没有任何子树,所以直接访问节点值Aor的右子树有左子树,则先访问其左子树- 左子树
not自己拥有一个左子树
not的左子树没有任何子树,直接访问其节点值B- 退回上一层,
not的子树都已被访问,现在访问其自身not
- 再退回上一层,
or的子树也都被访问过了,现在访问其自身or
- 再退回上一层,
and的子树也都被访问过了,现在访问其自身and
最终结果是['A', 'A', 'B', 'not', 'or', 'and']。
代码实现
def postOrderTraversal(tree):
l = []
if tree.firstChild() is not None:
l = l + postOrderTraversal(tree.firstChild())
if tree.secondChild() is not None:
l = l + postOrderTraversal(tree.secondChild())
l.append(tree.value[0])
return l
def buildTreeFrom(listFormInExpr):
tree = None
lastNode = None
for e in listFormInExpr:
node = buildExprNode(e)
tree, lastNode = insertIntoTreeFrom(tree, node, lastNode)
return tree
def insertIntoTreeFrom(tree, node, lastTouchedNode):
if tree is None:
return (node, node)
if node.value[0] == ')':
return insertRightBracket(tree, node, lastTouchedNode)
return insertOthers(tree, node, lastTouchedNode)
def insertRightBracket(tree, node, lastTouchedNode):
currentNode = lastTouchedNode
while currentNode is not None and currentNode.value[0] != '(':
currentNode = currentNode.parent
parent = currentNode.parent
parent.removeChild(currentNode)
parent.addChild(currentNode.firstChild())
return (tree, currentNode.firstChild())
def insertOthers(tree, node, lastTouchNode):
if node.value[1] > lastTouchNode.value[1]:
lastTouchNode.addChild(node)
return (tree, node)
currentNode = lastTouchNode
while currentNode.parent is not None and currentNode.value[0] != '(' and node.value[1] <= currentNode.value[1]:
currentNode = currentNode.parent
if currentNode.parent is None:
node.addChild(currentNode)
return (node, node)
node._children = currentNode._children
currentNode._children = []
currentNode.addChild(node)
return (tree, node)
def buildExprNode(symbol):
bracketSymbols = ['(', ')']
highPrecedenceOperators = ['not']
mediumPrecedenceOperators = ['and', 'nand', 'nor', 'xor', 'impl']
lowPrecedenceOperators = ['or', 'equ']
LOW_PRECEDENCE = 10
MEDIUM_PRECEDENCE = LOW_PRECEDENCE+1
HIGH_PRECEDENCE = MEDIUM_PRECEDENCE+1
BRACKET_PRECEDENCE = HIGH_PRECEDENCE+1
OPERAND_PRECEDENCE = BRACKET_PRECEDENCE+1
if symbol in bracketSymbols:
return Node((symbol, BRACKET_PRECEDENCE))
if symbol in highPrecedenceOperators:
return Node((symbol, HIGH_PRECEDENCE))
if symbol in mediumPrecedenceOperators:
return Node((symbol, MEDIUM_PRECEDENCE))
if symbol in lowPrecedenceOperators:
return Node((symbol, LOW_PRECEDENCE))
return Node((symbol, OPERAND_PRECEDENCE))
class Node:
def __init__(self, value):
self.value = value
self._children = []
self.parent = None
def addChild(self, node):
self._children.append(node)
node.parent = self
def removeChild(self, node):
self._children = [e for e in self._children if e.value != node.value]
def firstChild(self):
if len(self._children) > 0:
return self._children[0]
else:
return None
def secondChild(self):
if len(self._children) >=2:
return self._children[1]
else:
return None
单元测试
def test_buildTreeFrom():
treeA = buildTreeFrom(['A', 'and', 'B'])
assert treeA is not None
assert treeA.value[0] == 'and'
assert len(treeA._children) == 2
assert treeA._children[0].value[0] == 'A'
assert treeA._children[1].value[0] == 'B'
treeB = buildTreeFrom(['A', 'and', '(', 'A', 'or', 'not', 'B', ')'])
assert treeB is not None
assert treeB.value[0] == 'and'
assert len(treeB._children) == 2
assert treeB._children[0].value[0] == 'A'
assert treeB._children[1].value[0] == 'or'
assert len(treeB._children[1]._children) == 2
assert treeB._children[1]._children[0].value[0] == 'A'
assert treeB._children[1]._children[1].value[0] == 'not'
assert len(treeB._children[1]._children[1]._children) == 1
assert treeB._children[1]._children[1]._children[0].value[0] == 'B'
def test_postOrderTraversal():
assert postOrderTraversal(buildTreeFrom(['A', 'and', 'B'])) == [
'A', 'B', 'and']
assert postOrderTraversal(buildTreeFrom(['A', 'and', '(', 'A', 'or', 'not', 'B', ')'])) == [
'A', 'A', 'B', 'not', 'or', 'and']
将一串字符拆分为一组符号
确定有限状态自动机(deterministic finite automation,DFA)
在计算理论中,确定有限状态自动机或确定有限自动机(英语:deterministc finite automation,DFA)是一个能实现状态转移的自动机。对于一个给定的属于该自动机的状态和一个属于该自动机字母表的字元,它能根据事先给定的转移凾式转移到下一个状态(这个状态可腑是先前那个状态)。
定义
确定有限状态自动机A是由
- 一个非空有限的状态集合
- 一个输入字母表(非空有限的字元集合)
- 一个转移函式(例如:)
- 一个开始状态
- 一个接受状态的集合
所以组成的5元组。因此一个DFA可以写成这样的形式:。
工作方式
对于一个确定有限状态自动机,如果,我们就说该自动机接受字串w,反之则表明该自动机拒绝字串w。
被一个确定有限状态机接受的语言(或者叫「被辨识的语言」)定义为: ,也就是由所有被接受的字串组成的集合。
举个例子
确定有限状态自动机
由下面的状态转移表定义:
|0 |1
--|--|--
||
||
对应的转移函式为:
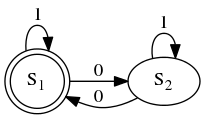
状态表示在输入的字串中有偶数个0,而表示有奇数个0。在输入中1不改变自动机的状态。当读完输入的字串的时候,状态将显示输入的字串是否包含偶数个0。
能辨识的语言是。用正规表示式表示为: 。
用有限状态自动机识别运算符中置表达式并拆分为符号
- 在状态时,输入空格,则不执行任何动作,并停留在当前状态
- 在状态时,输入字母,则将字母暂存,并转移至状态
- 在状态时,输入括号,则输出括号为一个符号,并停留在当前状态
- 在状态时,输入字母,则暂存字母,并停留在当前状态
- 在状态时,输入空格,则输出暂存中的字母为符号,清空暂存字母,并转移至状态
- 在状态时,输入括号,则输出暂存字母为符号,并转移至状态
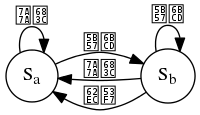
代码实现
def tokenize(exprInStr):
SA = 1
SB = 2
paren = ['(', ')']
space = [' ']
alphabet = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x',
'y', 'z', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z']
state = SA
tokens = []
wordCache = []
for e in exprInStr + ' ':
if state == SA and e in space:
# Nop
pass
elif state == SA and e in alphabet:
wordCache.append(e)
state = SB
elif state == SA and e in paren:
tokens.append(e)
# stay at SA
elif state == SB and e in alphabet:
wordCache.append(e)
# stay at SB
elif state == SB and e in space:
tokens.append(''.join(wordCache))
wordCache = []
state = SA
elif state == SB and e in paren:
tokens.append(''.join(wordCache))
wordCache = []
tokens.append(e)
state = SA
else:
pass
return [e for e in tokens if len(e) != 0]
单元测试
def test_tokenize():
assert tokenize('A and B') == ['A', 'and', 'B']
assert tokenize('A and (A or not B)') == [
'A', 'and', '(', 'A', 'or', 'not', 'B', ')']
完整实现
使用双层List Comprehension构建真值表,将具体值代入转换后的运算符后置表达式﹐计算出值。
# Truth tables for logical expressions (2)
# Contibue problem 3.01 by defining and/2, or/2, etc as being operators.
# this allows to write the logical expression in the more natural way,
# as in the example: AS and (A or not B).
# define operator precedence as usual; i.e. as in Java.
def table(la, lb, expr):
postExpr = postOrderTraversal(buildTreeFrom(tokenize(expr)))
return [(a,b,evaluate(resolveVariable(postExpr,{'A':a,'B':b}))) for a in la for b in lb]
def resolveVariable(expr, keyValues):
resolved = []
for e in expr:
if e in keyValues:
resolved.append(keyValues[e])
else:
resolved.append(e)
return resolved
def tokenize(exprInStr):
SA = 1
SB = 2
paren = ['(', ')']
space = [' ']
alphabet = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x',
'y', 'z', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z']
state = SA
tokens = []
wordCache = []
for e in exprInStr + ' ':
if state == SA and e in space:
# Nop
pass
elif state == SA and e in alphabet:
wordCache.append(e)
state = SB
elif state == SA and e in paren:
tokens.append(e)
# stay at SA
elif state == SB and e in alphabet:
wordCache.append(e)
# stay at SB
elif state == SB and e in space:
tokens.append(''.join(wordCache))
wordCache = []
state = SA
elif state == SB and e in paren:
tokens.append(''.join(wordCache))
wordCache = []
tokens.append(e)
state = SA
else:
pass
return [e for e in tokens if len(e) != 0]
def postOrderTraversal(tree):
l = []
if tree.firstChild() is not None:
l = l + postOrderTraversal(tree.firstChild())
if tree.secondChild() is not None:
l = l + postOrderTraversal(tree.secondChild())
l.append(tree.value[0])
return l
def buildTreeFrom(listFormInExpr):
tree = None
lastNode = None
for e in listFormInExpr:
node = buildExprNode(e)
tree, lastNode = insertIntoTreeFrom(tree, node, lastNode)
return tree
def insertIntoTreeFrom(tree, node, lastTouchedNode):
if tree is None:
return (node, node)
if node.value[0] == ')':
return insertRightBracket(tree, node, lastTouchedNode)
return insertOthers(tree, node, lastTouchedNode)
def insertRightBracket(tree, node, lastTouchedNode):
currentNode = lastTouchedNode
while currentNode is not None and currentNode.value[0] != '(':
currentNode = currentNode.parent
parent = currentNode.parent
parent.removeChild(currentNode)
parent.addChild(currentNode.firstChild())
return (tree, currentNode.firstChild())
def insertOthers(tree, node, lastTouchNode):
if node.value[1] > lastTouchNode.value[1]:
lastTouchNode.addChild(node)
return (tree, node)
currentNode = lastTouchNode
while currentNode.parent is not None and currentNode.value[0] != '(' and node.value[1] <= currentNode.value[1]:
currentNode = currentNode.parent
if currentNode.parent is None:
node.addChild(currentNode)
return (node, node)
node._children = currentNode._children
currentNode._children = []
currentNode.addChild(node)
return (tree, node)
def buildExprNode(symbol):
bracketSymbols = ['(', ')']
highPrecedenceOperators = ['not']
mediumPrecedenceOperators = ['and', 'nand', 'nor', 'xor', 'impl']
lowPrecedenceOperators = ['or', 'equ']
LOW_PRECEDENCE = 10
MEDIUM_PRECEDENCE = LOW_PRECEDENCE+1
HIGH_PRECEDENCE = MEDIUM_PRECEDENCE+1
BRACKET_PRECEDENCE = HIGH_PRECEDENCE+1
OPERAND_PRECEDENCE = BRACKET_PRECEDENCE+1
if symbol in bracketSymbols:
return Node((symbol, BRACKET_PRECEDENCE))
if symbol in highPrecedenceOperators:
return Node((symbol, HIGH_PRECEDENCE))
if symbol in mediumPrecedenceOperators:
return Node((symbol, MEDIUM_PRECEDENCE))
if symbol in lowPrecedenceOperators:
return Node((symbol, LOW_PRECEDENCE))
return Node((symbol, OPERAND_PRECEDENCE))
class Node:
def __init__(self, value):
self.value = value
self._children = []
self.parent = None
def addChild(self, node):
self._children.append(node)
node.parent = self
def removeChild(self, node):
self._children = [e for e in self._children if e.value != node.value]
def firstChild(self):
if len(self._children) > 0:
return self._children[0]
else:
return None
def secondChild(self):
if len(self._children) >=2:
return self._children[1]
else:
return None
def evaluate(exprInList):
stack = []
operatorBuilder = OperatorBuilder()
for e in exprInList:
if type(e) == bool:
stack.append(e)
else:
op = operatorBuilder.buildFor(e)
if op.isUnary():
a = stack.pop()
stack.append(op.apply(a))
elif op.isBinary():
a = stack.pop()
b = stack.pop()
stack.append(op.apply(a, b))
else:
raise "Unsupported operator " + e
return stack.pop()
class Operator:
def __init__(self, symbol):
self.symbol = symbol
def isUnary(self):
return False
def isBinary(self):
return False
def apply(self, a, b=None):
raise NotImplementedError
class Not(Operator):
def __init__(self):
super().__init__('not')
def isUnary(self):
return True
def apply(self, a):
return not a
class And(Operator):
def __init__(self):
super().__init__('and')
def isBinary(self):
return True
def apply(self, a, b):
return a and b
class Or(Operator):
def __init__(self):
super().__init__('or')
def isBinary(self):
return True
def apply(self, a, b):
return a or b
class Nand(Operator):
def __init__(self):
super().__init__('nand')
def isBinary(self):
return True
def apply(self, a, b):
return not (a and b)
class Nor(Operator):
def __init__(self):
super().__init__('nor')
def isBinary(self):
return True
def apply(self, a, b):
return not (a or b)
class Xor(Operator):
def __init__(self):
super().__init__('xor')
def isBinary(self):
return True
def apply(self, a, b):
return a != b
class Impl(Operator):
def __init__(self):
super().__init__('impl')
def isBinary(self):
return True
def apply(self, a, b):
return (not a) or b
class Equ(Operator):
def __init__(self):
super().__init__('equ')
def isBinary(self):
return True
def apply(self, a, b):
return a == b
class Nop(Operator):
def __init__(self):
super().__init__('op')
class OperatorBuilder:
def __init__(self):
self._operatorDefinition = {
Not().symbol: Not(),
And().symbol: And(),
Or().symbol: Or(),
Nand().symbol: Nand(),
Nor().symbol: Nor(),
Xor().symbol: Xor(),
Impl().symbol: Impl(),
Equ().symbol: Equ()
}
def buildFor(self, symbol):
if symbol in self._operatorDefinition:
return self._operatorDefinition[symbol]
else:
return Nop()
单元测试
def test_table():
assert table([True, False], [True, False], 'A and B') == [
(True, True, True),
(True, False, False),
(False, True, False),
(False, False, False)
]
assert table([True, False], [True, False], 'A and (A or not B)') == [
(True, True, True),
(True, False, True),
(False, True, False),
(False, False, False)
]














