Graphs

A preliminary remark: The vocabulary in graph theory varies considerably. Some authors use the same word with different meanings. Some authors use different words to mean the same thing. I hope that our definitions are free of contradictions.

图被定义为节点的集合和边的集合，其中每一条边都是由一对节点组成。

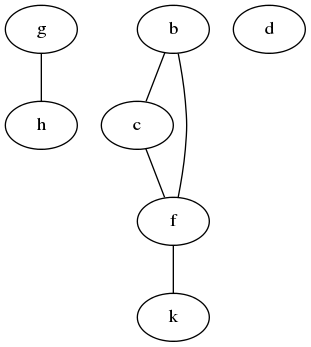
在Python中，有多种方式表示图。

一个方法是将每一条边分别表示成一句条文「clause」。按这种方式，图被描述成：

[(h,g), (k,f), (f,b), ...]

我们称之为边条文形式「edge-clause form」。

显然地，孤立的节点不能被表示出来。另一种方法是将整张图表示成一个数据对象。根据图的定义是一对集合（节点的和边的），我们可以使用以下Python数据结构表上述图例：

([b, c, d, g, h, k], [(b,c), (b, f), (c, f), (f, k), (g, h)])

我们称之为图项「graph-term form」。谨记，虽然这些列表都是有序的，但它们都是集合，不包含重复的元素。每一条边只在边列表𥚃出现一次；比如，一条从节点x到节点y的边被表示为(x, y)，边(y, x)是不会出现的。graph-term form是我们的默认形式。

第三种表现方法关联节点及相邻节点集合。我们称之为相邻列表形式「adjacency-kist form」。例如：

[(b, [c, f]), (c, [b, f]), (d, []), (f, [b, c, k])]

迄今为止，我们所介绍的表现形式都是便于自动处理的，但它们的语法都不用户友好。手写这些语句是繁琐及易错的。我们可以定义一种更紧凑及"人类友好的"的形式：一张图表示为一个以节点和二元组组成的列表。节点表示孤立节点，二元组表示边。如果X以边的端点出现，则其自动被定义为一个节点。我们的例子可以重写为：

[(b,c), (f, c), (g, h), d, (f, b), (k, f), (h, g)]

我们称之为人类友好形式「human-firendly form。如上所示，列表无需是有序的且有可能包含相同的边多次。注意孤立的节点d。

当边是有向时我们称之弧「arcs」。它们以二元组表示。其图被称为有向图「directed graph」（或者简称digraph）。为了表示有向图，之前讨论的形式需要简单修改。示例的图相应地表示为：

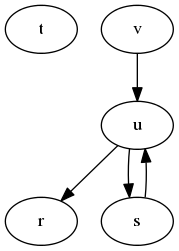
弧条文形式「Arc-clause form」

[(s, u), (u, r), ...]

图项形式「Graph-term form」

([r, s, t, u, v], [(s, r), (s, u), (u, r), (u, s), (v, u)])

相邻列表形式「Adjacency-list form」

[(r, []), (s, [r, u]), (t, []), (u, [r]), (v, [u])]

谨记，相郼列表形式无法区分无向图和有向图。

人类友好形式「Human-friendly form」

[(s, r), t, (u, r), (s, u), (u, s), (v, u)]

最后，无向图和有向图可能附加信息至节点和边（弧）。对节点，没有问题，只需简单地用二元组替换单一字符。另一方面，对于边则需要扩展我们的符法。在边上包有附加信息的图被称为标记图「labeled graphs」。

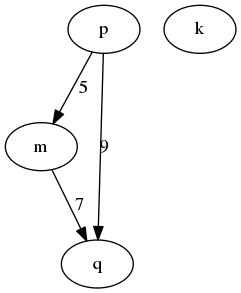
弧条文形式「Arc-clause form」

[(m, q, 7), (p, q, 9), (p, m, 5)]

图项形式「Graph-term form」

([k, m, p, q], [(m, p, 7), (p, m, 5), (p, q, 9)])

相邻列表形式「Adjacency-list form」

[(k, []), (m, [(q, 7)]), (p, [(m, 5), (q, 9)]), (q, [])]

注意，边信息被打包进二元组了。

人类友好形式「Human-friendly form」

[(p, q, 9], (m, q, 7), k, (p, m, 5)]

标记图的符号可以用于多重图「multi-graphs」，其允许在两点之间存在多条边（或弧）。