Depth-first order graph trabersal
题目
Write a predicate that generates a depth-first order graph traversal sequence. The starting point should be specified, and the output should be a list of nodes that are reachable from this starting point (in depth-first order).
解题思路
- 首先,获取一个可访问的点(相邻的且未被访问的)
- 然后,以该点为起点,重复步骤1和2,直至没有可访问的点(无相邻点或相邻点都已被访问)
举个例子,给定如下图:
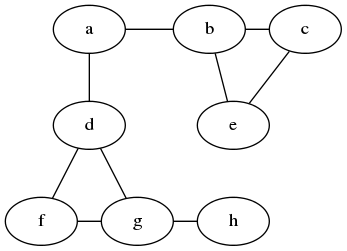
从a开始深度优先遍历。
- 以
a为起点,获取一个可访问的点b - 以
b为起点,获取一个可访问的点c - 以
c为起点,获取一个可访问的点e - 以
e为起点,无法获取一个可访问的点。相邻点都已被访问 - 退回至
c。以c为起点也无法获取一个可访问的点。相邻点都已被访问 - 退回
b。以b为起点也无法获取一个可访问的点。相邻点都已被访问 - 退回
a。以a为起点获取一个可访问的点d - 以
d为起点,获取一个可访问的点f - 以
f为起点,获取一个可访问的点g - 以
g为起点,获取一个可访问的点h - 以
h为起点,无法获取一个可访问的点。相邻点都已被访问 - 退回至
g。以g为起点也无法获取一个可访问的点。相邻点都已被访问 - 退回至
f。以f为起点也无法获取一个可访问的点。相邻点都已被访问 - 退回至
d。以d为起点也无法获取一个可访问的点。相邻点都已被访问 - 退回至
a。以a为起点也无法获取一个可访问的点。相邻点都已被访问
至此,完成图的深度优先遍历,得到序列[a, b, c, e, d, f, g, h]。
代码实现
def traversal(g, start):
return doTraversal(g, start, [])
def doTraversal(g, start, accessedNodes):
accessedNodes = accessedNodes + [start]
nextNode = findNext(g, start, accessedNodes)
while nextNode is not None:
accessedNodes = doTraversal(g, nextNode, accessedNodes)
nextNode = findNext(g, start, accessedNodes)
return accessedNodes
def findNext(g, start, accessedNodes):
adjacentNodes = adjacent(g, start)
availableNodes = [
node for node in adjacentNodes if node not in accessedNodes]
if len(availableNodes) == 0:
return None
else:
return availableNodes[0]
def adjacent(g, node):
for edge in g[1]:
if edge[0] == node:
yield edge[1]
if edge[1] == node:
yield edge[0]